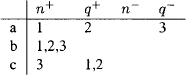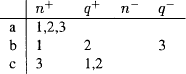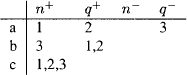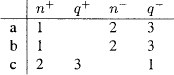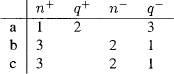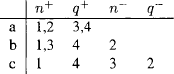Aristotle’s Modal Syllogisms
Considering Aristotle’s discussion of syllogisms as a whole, the most striking point is that its focus is the modal syllogisms – This is the point on which the logical tradition has diverged most completely from Aristotle, as a rule giving no attention to modal syllogisms.…
Aristotle’s system of modal syllogisms, to be found in chapters 3 and 8–22 of the first book of the Prior Analytics, has been open to public inspection for over 2300 years. And yet perhaps no other piece of philosophical writing has had such consistently bad reviews.
… by raising the [completeness] problem, Aristotle earns the right to be considered not only the father of logic, but also the (grand)father of meta- logic.
Storrs McCall [1963] developed the first formal system, the L-X-M calculus, for which a decision procedure for assertion or rejection of formal sentences is given that has any chance of matching Aristotle’s judgments about which of the n-premised (for n ≥ 2) “apodeictic syllogisms” are valid or invalid. McCall’s remarkable results were achieved by extending Jan Łukasiewicz’s [1957] decision procedure for assertion or rejection of expressions in his formal system, ŁA, that is designed to capture Aristotle’s judgments about which of the “assertoric (or plain1) syllogisms” are valid or invalid.
Łukasiewicz also considers using his four-valued modal system, the ŁM system, to present Aristotle’s syllogistic but finds that the match is not very good. Peter Geach also proposes a system for dealing with the apodeictics. But, again, the match is not very good. After examining McCall’s L-X-M system and work related to it we shall turn to his work on the “contingent syllogisms”. His purely syntactic system, Q-L-X-M, has some unAristotelian features that lead us to develop a modified system, QLXM’. A semantics for QLXM’ is developed that enables us to provide formal countermodels for a large percentage of the assertoric, apodeictic or contingent syllogisms that Aristotle explicitly considered to be invalid.
1 Łukasiewicz’s Assertoric System, Ła
For Łukasiewicz, Aristotle’s syllogisms are “implicational” rather than “inferential”. He says in [1957, p. 21]:
are not Aristotelian. We do not meet them until Alexander. This transference of the Aristotelian syllogisms from the implicational form into the inferential is probably due to the Stoics.
So, Łukasiewicz claims Aristotle construed the above syllogism, with traditional name ‘Barbara’, as a conditional claim:
Robin Smith’s [1989, p.4] translation of Barbara at Prior Analytics 25b37–40 seems to conform with Łukasiewicz’s view:
… if A is predicated of every B and B of every C, it is necessary for A to be predicated of every C .…
But see [Corcoran, 1972] and [Smiley, 1973] for the view that Aristotle developed natural deduction systems rather than the axiomatic systems of the sort Łukasiewicz envisages.
Łukasiewicz uses Polish notation, a parenthesis-free notation, to express the well-formed formulas (wffs) in his formal system, which we refer to as ŁA. We replace his notation with current “standard” notation when giving the basis for it.2 So, for example, his Cpq (‘If p then q’) is our (p → q). His Np (‘not p’) and Kpq (‘p and q’) are our ¬p and (p ∧ q), respectively.
Łukasiewicz’s assertions and rejections are marked by  and
and  , respectively. The system that is essentially Łukasiewicz’s will be called ŁA.
, respectively. The system that is essentially Łukasiewicz’s will be called ŁA.
So, for example,  (Aba → (Acb → Aca)) says that Barbara is asserted in ŁA, which is true.
(Aba → (Acb → Aca)) says that Barbara is asserted in ŁA, which is true.  Aba says that Aba is rejected in ŁA, which is true. Assertions and rejections are relative to systems. We shall avoid using
Aba says that Aba is rejected in ŁA, which is true. Assertions and rejections are relative to systems. We shall avoid using  ŁA, say, and rely on the context to indicate that the assertion is relative to system ŁA.
ŁA, say, and rely on the context to indicate that the assertion is relative to system ŁA.
Primitive Symbols
| term variables | a, b, c,… (with or without subscripts) |
| monadic operator | ¬ |
| dyadic operator | → |
| quantifiers | A, I |
| parentheses | (,) |
Formation rules
| FR1 | If Qu is a quantifier and x and y are term variables then Quxy is a wff. |
| FR2 | If p and q are wffs then ¬p and (p → q) are wffs. |
| FR3 | The only wffs are those in virtue of FR1 and FR2. |
So, for example, Aab, Iab and (Abc → ¬Ibc) are wffs. Read them as “All a are b’, ‘Some a are b’ and ‘If all b are c then it is not true that some b are c’, respectively.
Definitions
| Def∧ | (p ∧ q) =df ¬(p → ¬q) |
| Def | (p q) =df (p → q) ∧ (q ← p)) |
| Def E | Exy =df ¬Ixy |
| Def O | Oxy =df ¬Axy |
Eab and Oab may be read as ‘No a are b’ and ‘Some a are not b’, respectively.
Łukasiewicz’s ŁA contains theses that are “assertions” (indicated by  ) as well as theses that are “rejections” (indicated by
) as well as theses that are “rejections” (indicated by  ). We begin with the former, which are generated by assertion axioms and assertion rules.
). We begin with the former, which are generated by assertion axioms and assertion rules.
Assertion axioms
| A0 (PC). | If p is a wff that is valid in virtue of the propositional calculus (PC) then  p (that is, p is asserted). (So, for example, p (that is, p is asserted). (So, for example,  (Aab → Aab) since it is not possible that the antecedent Aab is true and the consequent Aab is false. And (Aab → Aab) since it is not possible that the antecedent Aab is true and the consequent Aab is false. And  ((Aab → Iab) → (¬Iab → ¬Aab)) since it is not possible that all of these conditions are met: (Aab → Iab) is true, ¬Iab is true and ¬Aab is false.) ((Aab → Iab) → (¬Iab → ¬Aab)) since it is not possible that all of these conditions are met: (Aab → Iab) is true, ¬Iab is true and ¬Aab is false.) |
| A1 |  Aaa Aaa |
| A2 |  Iaa Iaa |
| A3 (Barbara) |  (Abc → (Aab → Aac)) (Abc → (Aab → Aac)) |
| A4 (Datisi) |  (Abc → (Iba → Iac)) (Abc → (Iba → Iac)) |
Transformation rules for assertions
| Ar1 | (Uniform substitution for assertions, US) From  p infer p infer  q (that is, from the assertion of p infer the assertion of q) provided q is obtained from p by uniformly substituting variables for variables. (So, for example, from q (that is, from the assertion of p infer the assertion of q) provided q is obtained from p by uniformly substituting variables for variables. (So, for example, from  (Aab → Iba) we may infer (Aab → Iba) we may infer (Acb → Ibc) and (Acb → Ibc) and  (Abb → Ibb), by rule US. But rule US does not permit us to infer that (Abb → Ibb), by rule US. But rule US does not permit us to infer that  (Aab → Iba) given that (Aab → Iba) given that  (Abb →Ibb). (Abb →Ibb). |
| Ar2 | (Modus Ponens, MP) From  (p →q) and (p →q) and  p infer p infer  q. q. |
| Ar3 | (Definiens and definiendum interchange for assertions, DDI) From  (…α…) and α =df β infer (…α…) and α =df β infer  (…β…), and vice versa. (So, for example, from (…β…), and vice versa. (So, for example, from  (¬Iab → ¬Aab) infer (¬Iab → ¬Aab) infer  (Eab →Oab) by two uses of DDI, given definitions Def E and Def O. Typically a use of DDI will be indicated by simply referring to a definition that is used. So, from (¬Iab → ¬Aab) infer (Eab →Oab) by two uses of DDI, given definitions Def E and Def O. Typically a use of DDI will be indicated by simply referring to a definition that is used. So, from (¬Iab → ¬Aab) infer  (Eab → ¬Aab) by Def E. It is to be understood that DDI is also used.) (Eab → ¬Aab) by Def E. It is to be understood that DDI is also used.) |
Given the assertion portion of the basis for ŁA, we shall give some “assertion deductions” — sequences of wffs such that each member of the sequence is either an assertion axiom or is entered from a prior member of the sequence by using a transformation rule for assertions — that capture some Aristotelian principles involving conversions, subordinations, and oppositions.
The above reasoning may be presented more succinctly by using the following derived rule for assertions.
Proof: i) Suppose  (p → q). By A0
(p → q). By A0  ((p → q) → (¬q → ¬p)). By MP
((p → q) → (¬q → ¬p)). By MP  (¬q → ¬p). ii) Suppose
(¬q → ¬p). ii) Suppose  (p → (q → r)). By A0
(p → (q → r)). By A0  ((p → (q → r)) → (p → (¬r → ¬q))). By MP
((p → (q → r)) → (p → (¬r → ¬q))). By MP  (p → (¬r → ¬q))). Use similar reasoning for iii).
(p → (¬r → ¬q))). Use similar reasoning for iii).
So, the annotation for line 7 in the above deduction may read: ‘(from 4 by RV)’. Line 6 may be deleted.
The following derived rules are useful in generating other principles.
(Assertion by antecedent strengthening (or equivalence), AS) From  (p →(q →r)) and
(p →(q →r)) and  (s →q) infer
(s →q) infer  (p →(s →r)); and from
(p →(s →r)); and from  (p →(q →r)) and
(p →(q →r)) and  (s →p) infer
(s →p) infer  (s →(q →r)).3
(s →(q →r)).3
(Assertion by consequent weakening (or equivalence), CW) From  (p →q) and
(p →q) and  (q →r) infer
(q →r) infer  (p →r); and from
(p →r); and from  (p →(q →r)) and
(p →(q →r)) and  (r →s) infer
(r →s) infer  (p →(q →s)).4
(p →(q →s)).4
To prove DR3 and DR4 use A0 and MP.
Theorem 1.3: (Assertoric conversion per accidens, Con(pa)) i)  (Aab → Iba); and ii)
(Aab → Iba); and ii)  (Eab → Oba).5
(Eab → Oba).5
The following derived rule, proven by using AO and MP, is useful in proving the next theorem.
Proof: Suppose  (p → q) and
(p → q) and  (q → p). By A0,
(q → p). By A0,  ((p → q) → ((q → p) → (p q))). By two uses of MP,
((p → q) → ((q → p) → (p q))). By two uses of MP,  (p q).
(p q).
Theorem 1.4: (Assertoric oppositions, Opp) i)  (¬Aab Oab); ii)
(¬Aab Oab); ii)  (¬Eab Iab); iii) (¬Iab Eab); and iv) (¬Oab Aab).
(¬Eab Iab); iii) (¬Iab Eab); and iv) (¬Oab Aab).
2.  (¬Aab → Oab) (from 1 by Def O)
(¬Aab → Oab) (from 1 by Def O)
3.  (Oab → ¬Aab) (from 1 by Def O)
(Oab → ¬Aab) (from 1 by Def O)
4.  (¬Aab Oab) (i, from 2 and 3 by BIC)
(¬Aab Oab) (i, from 2 and 3 by BIC)
8.  (¬Eab → Iab) (from 6 and 7 by CW)
(¬Eab → Iab) (from 6 and 7 by CW)
9.  (¬¬Iab → ¬¬Eab) (from 5 by Def E)
(¬¬Iab → ¬¬Eab) (from 5 by Def E)
11.  (Iab → ¬Eab) (from 10 and 9 by CW)
(Iab → ¬Eab) (from 10 and 9 by CW)
12.  (¬Eab Iab) (ii, from 11 by BIC)
(¬Eab Iab) (ii, from 11 by BIC)
13.  ((¬Aab Oab) → (¬ Aab)) (by A0)
((¬Aab Oab) → (¬ Aab)) (by A0)
14.  (¬Oab Aab) (iv, from 4 and 13 by MP)
(¬Oab Aab) (iv, from 4 and 13 by MP)
The following derived rule is useful in conjunction with the assertoric oppositions.
So, for example, from  (Aab → (Abc → (¬Aad → ¬Acd))) infer
(Aab → (Abc → (¬Aad → ¬Acd))) infer  (Aab → (Abc → (Oad → Ocd))) by SE, given the oppositions Opp.
(Aab → (Abc → (Oad → Ocd))) by SE, given the oppositions Opp.
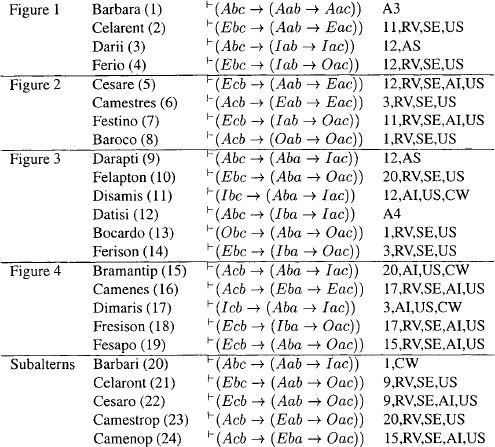
On table 1 assertions corresponding to the familiar two-premised syllogisms are listed. In the right column a method of deducing the assertion is given. So, for example, Barbara is trivially asserted by using axiom A3. Celarent is asserted since the assertion of 11 (Disamis) may be transformed into  (¬Iac → (Aba → ¬Ibc)) (by RV), which may be transformed into
(¬Iac → (Aba → ¬Ibc)) (by RV), which may be transformed into  (Eac → (Aba → Ebc)) (by SE, since
(Eac → (Aba → Ebc)) (by SE, since  (Eac ¬Iac) and
(Eac ¬Iac) and  (Ebc ¬Ibc)), which may be transformed into 2 (by US, putting ‘b’ in place of ‘a’ and ‘a’ in place of ‘b’). Darii is asserted since the assertion of 12 may be transformed into
(Ebc ¬Ibc)), which may be transformed into 2 (by US, putting ‘b’ in place of ‘a’ and ‘a’ in place of ‘b’). Darii is asserted since the assertion of 12 may be transformed into  (Abc → (Iab → Iac)) (by AS, since (Iab → Iba)).
(Abc → (Iab → Iac)) (by AS, since (Iab → Iba)).
1.1 Rejection in ŁA
Łukasiewicz uses the notion of “rejection” to develop his formal system.7 He shows that the invalid syllogistic forms expressed by “elementary wffs” may be rejected by augmenting his formal system for assertions by adding one rejection axiom and four transformation rules that generate rejections. We shall illustrate this claim but not give a full account of Łukasiewicz’s work on rejections, which would require showing that all wffs may be “reduced” to sets of elementary wffs.
Rejection transformation rules for ŁA
| Rr1 | (Rejection by uniform substitution, R-US) If  x and x is obtained from y by uniform substitution of terms for terms, then x and x is obtained from y by uniform substitution of terms for terms, then  y. y. |
| Rr2 | (Rejection by detachment (or Modus Tollens), R-D) From  (x → y) and (x → y) and  y infer y infer  x. x. |
| Rr3 | (Słupecki’s rejection rule, R-S) From  (x →z) and (x →z) and  (y →z) infer (y →z) infer  (x →(y →z)) provided: i) x and y have form ¬Apq or ¬Ipq; and ii) z has form (x1 → (x2 → (x3 → … xn)…) where each xi is a simple sentence. (x →(y →z)) provided: i) x and y have form ¬Apq or ¬Ipq; and ii) z has form (x1 → (x2 → (x3 → … xn)…) where each xi is a simple sentence. |
| Rr4 | (Definiens and definiendum interchange for rejections, R-DDI) From  (… α …) and α =df β infer (… α …) and α =df β infer  (…β…), and vice versa. (So, for example, from (…β…), and vice versa. (So, for example, from  (¬Aab → ¬Iab) infer (¬Aab → ¬Iab) infer  (Eab → Oab) by two uses of R-DDI, given definitions Def O and Def E.) (Eab → Oab) by two uses of R-DDI, given definitions Def O and Def E.) |
The following derived rules for rejections, which are counterparts of derived rules for assertions, are useful in simplifying presentations of rejection deductions — sequences of wffs in which each member of the sequence is either an (assertion or rejection) axiom or is entered by an (assertion or rejection) transformation rule, where the last member of the sequence is a rejection.
Proof: i) Suppose  (p → q). By A0 (or PC)
(p → q). By A0 (or PC)  ((¬q → ¬p) → (p → q)). By R-D
((¬q → ¬p) → (p → q)). By R-D  (¬q → ¬p). ii) Suppose
(¬q → ¬p). ii) Suppose  (p → (q → r)). By A0
(p → (q → r)). By A0  ((p → (¬r → ¬q)) → (p → (q → r))). By R-D
((p → (¬r → ¬q)) → (p → (q → r))). By R-D  (p → (¬r → ¬g)). Use similar reasoning for iii).
(p → (¬r → ¬g)). Use similar reasoning for iii).
Proof: Suppose  (p → (q → r)) and
(p → (q → r)) and  (q → s). By AO
(q → s). By AO  ((q → s) → ((p → (s → r)) → (p → (q → r)))). By MP
((q → s) → ((p → (s → r)) → (p → (q → r)))). By MP  ((p → (s → r)) → (p → (q → r))). By R-D
((p → (s → r)) → (p → (q → r))). By R-D  (p → (s → r)). Use similar reasoning for ii).
(p → (s → r)). Use similar reasoning for ii).
Proofs for the following two derived rules are easily constructed and will be omitted.
Given the above apparatus we are able to show how the four syllogisms referred to at Prior Analytics 26a2–9 are rejected in ŁA. This is Łukasiewicz’s translation from [1957, p. 67].
If the first term belongs to all the middle [Aba], but the middle to none of the last [Ecb], there will be no syllogism of the extremes; for nothing necessary follows from the terms being so related; for it is possible that the first should belong to all as well as to none of the last, so that neither a particular nor a universal conclusion is necessary. But if there is no necessary consequence by means of these premises, there cannot be a syllogism. Terms of belong to all: animal, man, horse; to none: animal, man, stone.
The four syllogisms are (Aba → (Ecb → x)), where x is Ica, Oca, Aca or Eca. We shall give rejection deductions to establish the rejection of the first two (AEI-1 and AEO-1) and then use derived rule R-CS to show the last two (AEA-1 and AEE-1) are rejected,8
1.  (Acb → (Aab → Iac)) (by R1)
(Acb → (Aab → Iac)) (by R1)
2.  (Iac → (Acb → (Aab → Iac))) (by A0)
(Iac → (Acb → (Aab → Iac))) (by A0)
5.  (Acc → Iac) (from 3 and 4 by R-II)
(Acc → Iac) (from 3 and 4 by R-II)
6.  (Acb → Iab) (from 5 by R-US)
(Acb → Iab) (from 5 by R-US)
7.  (Eab → Ocb) (from 6 by R-RV and R-SE)
(Eab → Ocb) (from 6 by R-RV and R-SE)
8.  (Acb → Iac) (from 5 by R-US)
(Acb → Iac) (from 5 by R-US)
9.  (Eac → Ocb) (from 8 by R-RV and R-SE)
(Eac → Ocb) (from 8 by R-RV and R-SE)
10.  (Eab → (Eac → Ocb)) (from 7 and 9 by R-S)
(Eab → (Eac → Ocb)) (from 7 and 9 by R-S)
1.  (Aba → (Ecb → Ice)) (by theorem 1.6)
(Aba → (Ecb → Ice)) (by theorem 1.6)
3.  (Aba → (Ecb → Aca)). (i, from 1 and 2 by R-CS)
(Aba → (Ecb → Aca)). (i, from 1 and 2 by R-CS)
4.  (Aba → (Ecb → Oca)) (by theorem 1.7)
(Aba → (Ecb → Oca)) (by theorem 1.7)
The following passage clearly shows that Ross favors Łukasiewicz’s method of rejecting the AEx-ls over Aristotle’s. On p. 302 of [1949] Ross says:
… [Aristotle] gives no reason (my italics) for this [claim that no conclusion is yielded by the premises of AEx-1], e.g. by pointing out that an undistributed middle or an illicit process is involved; but he often points to an empirical fact. …instead of giving the reason why All B are A, No C is B yields no conclusion, he simply points to one set of values for A, B, C (animal, man, horse) for which, all B being A and no C being B, all C is in fact A, and to another set of values (animal, man, stone) for which, all B being A and no C being B, no C is in fact A. Since in the one case all C is A, a negative conclusion cannot be valid; and since in the other case no C is A, an affirmative conclusion cannot be valid. Therefore there is no valid conclusion (with C as subject and A as predicate).
Aristotle is reasoning as follows. It is true that all men are animals, it is true that no horses are men, and it is true that all horses are animals (and thus false that no horses are animals and false that some horses are not animals). So neither Eca nor Oca is a logical consequence of Aba together with Ecb. Since it is true that all men are animals, it is true that no stones are men, and it is true that no stones are animals (and thus false that all stones are animals and false that some stones are not animals), it follows that neither Aca nor Ica is a logical consequence of Aba together with Ecb.
Łukasiewicz also objects to Aristotle’s reasoning, claiming in [1957, p. 72] that it:
introduces into logic terms and propositions not germane to it. ‘Man’ and ‘animal’ are not logical terms, and the proposition ‘All men are animals’ is not a logical thesis. Logic cannot depend on concrete terms and statements. If we want to avoid this difficulty, we must reject some forms axiomatically.
But Aristotle’s procedures have support among modern logicians. Robin Smith [1989, p. 114] regards Aristotle’s reference to animals, men and horses as a reference to a “countermodel” and says “countermodels are the paradigmatic means of proving invalidity for modern logicians.” In the surrounding text Smith refers to Jonathan Lear [1980, pp. 54–61 and pp. 70–75] who defends Aristotle’s techniques against criticisms by Łukasiewicz and Geach [1972]. In the following sections we shall make extensive use of formal countermodels to show the invalidity of apodeictic and contingent syllogisms. Such models may also be used to show the invalidity of assertoric syllogisms.
The following passage from the Prior Analytics 27b12–23, quoted and discussed by Łukasiewicz on p. 70 of [1957], illustrates another method Aristotle uses to reject inferences. Ross [1949, p. 304] calls it an argument “from the ambiguity of a particular proposition.” A better name for the reasoning is “rejection by premise weakening”. Ross points out that this method of rejection is also used by Aristotle at 26b14–20, 27b27–28, 28b28–31,29a6 and 35b11.
Let M belong to no N, and not to some X. It is possible then for N to belong either to all X or to no X. Terms of belonging to none: black, snow, animal. Terms of belonging to all cannot be found, if M belongs to some X, and does not belong to some X. For if N belonged to all X, and M to no N, then M would belong to no X; but it is assumed that it belongs to some X. In this way, then, it is not possible to take terms, and the proof must start from the indefinite nature of the particular premise. For since it is true that M does not belong to some X, even if it belongs to no X, and since if it belongs to no X a syllogism is not possible, clearly it will not be possible either.
Given the semantic consistency of {No snow is black, Some animals are not black, No animal is snow} we know by half of the “contrasted instances” argument that neither ‘Some animal is snow’ nor ‘All animals are snow’ is a logical consequence of ‘No snow is black’ together with ‘Some animals are not black.’ So, a “countermodel” is given for the inferences from Enm and Oxm to Ixn or Axn. To show that neither Oxn nor Exn is a semantic consequence of Enm and Oxm, Aristotle relies on two facts: i) neither Oxn nor Exn is a semantic consequence of Enm and Exm; and ii) Oxm is a semantic consequence of Exm.
In ŁA a purely syntactic rejection of the “implicational syllogisms” (Enm → (Oxm → Oxn)) and (Enm → (Oxm → Exn)) is given by using R-AW.
1.  (Aba → (Ecb → Ica)) (by theorem 1.6)
(Aba → (Ecb → Ica)) (by theorem 1.6)
2.  (Eca → (Ecb → Oba)) (from 1 by R-RV and R-SE)
(Eca → (Ecb → Oba)) (from 1 by R-RV and R-SE)
3.  (Ecb → Obc) (by Con(pa) and US)
(Ecb → Obc) (by Con(pa) and US)
4.  (Eca → (Obc Oba)) (from 2 and 3 by R-AW)
(Eca → (Obc Oba)) (from 2 and 3 by R-AW)
5.  (Eca → Eac) (by Con and US)
(Eca → Eac) (by Con and US)
6.  (Eac → (Obc → Oba)) (from 4 and 5 by R-AW)
(Eac → (Obc → Oba)) (from 4 and 5 by R-AW)
7.  (Enm → (Oxm → Oxn)) (i, from 4 by R-US)
(Enm → (Oxm → Oxn)) (i, from 4 by R-US)
Up to this point we have rejected elementary wffs of form (x1 → (x2 → … (xn → y)…) where n ≤ 2. For Łukasiewicz’s system to be fully Aristotelian he must show how elementary sentences, where n > 2, are rejected. We illustrate such a rejection.
1.  (Acb → (Aab → Iac)) (by R1)
(Acb → (Aab → Iac)) (by R1)
2.  (Acb → (Aba → Iac)) (by Bramantip)
(Acb → (Aba → Iac)) (by Bramantip)
3.  ((Acb → (Aba → Iac))mc(Acb → (Aab → Iac)) (from 2 and 1 by R-II)
((Acb → (Aba → Iac))mc(Acb → (Aab → Iac)) (from 2 and 1 by R-II)
4.  ((Aba → Aab) → ((Acb → (Aba → Iac))mc(Acb → (Aab → Iac))) (by A0)
((Aba → Aab) → ((Acb → (Aba → Iac))mc(Acb → (Aab → Iac))) (by A0)
5.  (Aba → Aab) (from 3 and 4 by R-D)
(Aba → Aab) (from 3 and 4 by R-D)
7.  (Aaa → (Aba → Aab)) (from 6 and 5 by R-II)
(Aaa → (Aba → Aab)) (from 6 and 5 by R-II)
8.  (Aaa → (Aaa → (Aba → Aab))) (from 7 and 5 by R-II)
(Aaa → (Aaa → (Aba → Aab))) (from 7 and 5 by R-II)
9.  (Aaa → (Aaa → (Ada → Aad))) (from 8 by R-US)
(Aaa → (Aaa → (Ada → Aad))) (from 8 by R-US)
Łukasiewicz’s system for the assertoric syllogistic has “100% Aristotelicity”, to use McCall’s expression. This means that every 2-premised syllogism deemed valid by Aristotle is asserted in Łukasiewicz’s system, and every 2-premised syllogism deemed invalid by Aristotle is rejected in Łukasiewicz’s system. We shall see below that McCall’s L-X-M calculus also has 100% Aristotelicity though his Q-L-X-M calculus does not.
2 Łukasiewicz’s Modal System, ŁM
Łukasiewicz developed his system for the assertoric syllogistic by using the non-modal propositional calculus, what he calls the “theory of deduction” as a “base logic”. Following the procedure used in Hughes and Cresswell’s [1968] and [1996], we simplified Łukasiewicz’s presentation of his system by simply using axiom A0 to provide his “basis”. Łukasiewicz’s approach to Aristotle’s modal logic is to develop a modal propositional logic (with quantifiers), which we refer to as the “ŁM system”, that will enable him to present Aristotle’s work on the modal syllogisms.9
The following sentences are tautologies in ŁM, modifying Łukasiewicz’s notation in a natural way: 1) ((p → q) → (Mp → Mq)) and 2) ((p → q) → (Lp → Lq)), reading M and L as ‘it is possible that’ and ‘it is necessary that’, respectively. The following passages on p. 138 of [Łukasiewicz, 1957] attempt to show that the “M-law of extensionality” (1) and the “L-law of extensionality” (2) are endorsed by Aristotle.
First it has to be said that if (if α is, β must be), then (if α is possible, β must be possible too).
If one should denote the premises by α, and the conclusion by β, it would not only result that if α is necessary, then β is necessary, but also that if α is possible, then β is possible.
A more natural reading of these passages is that they show that Aristotle endorsed both 3) (L(p Ł q) → (Mp → Mq)) and 4) (L(p → q) → (Lp → Lq)).10
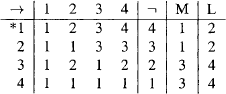
That l) – 4) are tautologies in ŁM is seen by considering the following four-valued truth tables.
Among the four truth values 1 to 4, 1 is the only designated value, marked with an asterisk in its entry in the first column on the table. A sentence x in the ŁM-system is a tautology iff for every input of values the output value is always the designated value 1.
Proof: Suppose ((p → q) → (Lp → Lq)) is assigned a value other than 1. Then i) (p → q) is not assigned 4 and ii) (Lp → Lq) is not assigned 1, and iii) the value assigned to (p → q) is not the value assigned to (Lp → Lq). By i) p is not assigned 1 and q is not assigned 4. By ii) Lp is not assigned 4 and thus p is assigned neither 3 nor 4. And by ii) Lp is not assigned the same value as Lq. So p is assigned the value 2 and q is assigned the value 3. Then (p → q) and (Lp → Lq) are assigned the same value, which conflicts with iii).
Proofs that 1), 3) and 4) are tautologies are not required for our purposes, and we omit the straightforward proofs.
McCall [1963, pp. 31–32] points out that Łukasiewicz’s use of the L-law of extensionality yields highly unAristotelian results. For example, using McCall’s notation, Camestres LXL (‘Necessarily all c are b; no a are b; so (necessarily) necessarily no a are c’), Baroco LXL (‘Necessarily all c are b; some a are not b; so necessarily some a are not c’), Barbara XLL (‘All b are c; necessarily a are b; so necessarily all a are c’) and Ferio XLL (‘No b are c; necessarily some a are b; so necessarily some b are c’), when construed as “implicational syllogisms”, are asserted in Łukasiewicz’s Ł-system even though Aristotle rejects all of them.
Following McCall we use ‘XXX’ after the name of a syllogism to indicate that the syllogism is a plain, assertoric syllogism. So, for example, Camestres XXX has form ‘All c are b; no a are b; so no a are c’. Camestres XXX, Baroco XXX, Barbara XXX and Ferio XXX are asserted in Łukasiewicz’s assertoric system. So, given the following theorem, Camestres LXL, Baroco LXL, Barbara XLL and Ferio XLL are asserted in Łukasiewicz’s Ł-system.
1.  ((q → r) → (Lq → Lr)) (by theorem 2.1)
((q → r) → (Lq → Lr)) (by theorem 2.1)
2.  (((q → r) → (Lq → Lr)) → ((p → (q → r)) → (p → (Lq → Lr))) (by A0)
(((q → r) → (Lq → Lr)) → ((p → (q → r)) → (p → (Lq → Lr))) (by A0)
3.  ((p → (q → r)) → (p → (Lq → Lr))) (i, from 1 and 2 by MP)
((p → (q → r)) → (p → (Lq → Lr))) (i, from 1 and 2 by MP)
4.  (((p → (q → r)) → (p → (Lq → Lr)) → ((q → (p → r)) → (Lq → (p → Lr))) (by A0)
(((p → (q → r)) → (p → (Lq → Lr)) → ((q → (p → r)) → (Lq → (p → Lr))) (by A0)
One of the virtues of McCall’s L-X-M calculus, discussed below, is that Camestres LXL, Baroco LXL, Barbara XLL and Ferio XLL are rejected in it. But before we examine McCall’s system we look briefly at some recent systems of modal predicate logic that have been used to attempt to understand Aristotle’s work on the modal syllogisms.
3 Modern Modal Predicate Logic
It is natural to try to view Aristotle’s modal logic through the eyes of modern modal monadic first order predicate logic.11 On pp. 18–22 McCall refers to Albrecht Becker’s [1933]12 and works by others who have tried to do this. On pp. 176–181 Patterson discusses Ulrich Nortmann’s [1990] attempt to do this. Patterson points out that the Kripkean “possible worlds semantics” used by Nortmann does not conform with Aristotle’s ontological principles. I agree. McCall argues that all uniform readings of Aristotle’s modal propositions as sentences in a modal first order predicate logic will make some valid Aristotelian syllogisms invalid or will make some invalid Aristotelian syllogisms valid. I also agree with McCall and will give some examples that support his position.
To illustrate how invalid Aristotelian inferences may be made valid consider Bocardo LXL, (that is, ‘LObe, Aba; so LOac’, using McCall’s notation). Suppose we translate it into modal predicate logic as: ‘∃x(Bx∧ ¬Cx); ∀x(Bx → Ax); so ∃x(Ax∧
¬Cx); ∀x(Bx → Ax); so ∃x(Ax∧ ¬Cx)’ (that is, ‘There is an x such that x is a B and x is necessarily not a C; for all x if x is a B then x is an A; so there is an x such that x is an A and x is necessarily not a C’). We are using one of Becker’s two methods for translating LO sentences. Using “singular sentences” such as Bm (read as m is a B, for ‘Max is a bear’, for example) and familiar rules such as Existential Instantiation (EI)13, Universal Instantiation (UI) and Existential Generalization (EG) together with propositional calculus (PC) inferences we may construct a deduction for Bocardo LXL, which Aristotle considered to be invalid.14
¬Cx)’ (that is, ‘There is an x such that x is a B and x is necessarily not a C; for all x if x is a B then x is an A; so there is an x such that x is an A and x is necessarily not a C’). We are using one of Becker’s two methods for translating LO sentences. Using “singular sentences” such as Bm (read as m is a B, for ‘Max is a bear’, for example) and familiar rules such as Existential Instantiation (EI)13, Universal Instantiation (UI) and Existential Generalization (EG) together with propositional calculus (PC) inferences we may construct a deduction for Bocardo LXL, which Aristotle considered to be invalid.14
To illustrate how valid Aristotelian inferences may be made invalid, consider Bocardo LLL, (that is, ‘LObc; LAba; so LOac’, using McCall’s notation). Using another Becker translation of LO sentences and a Becker translation of LA sentences the argument amounts to this: ∀x(Cx →  Bx); ∃x(
Bx); ∃x( Ax ∧
Ax ∧  ¬Bx); so ∃x(
¬Bx); so ∃x( Ax ∧
Ax ∧  ¬Cx), call it the “the MPredC argument”. Aristotle at [30a6–14] gives a proof by ecthesis to show that Bocardo LLL is valid. But using the semantics for the modal system, S5, the translated argument is S5-invalid. For suppose there are only two possible worlds w1 and w2, where each world “sees” each world (including itself). If “the MPredC argument” is S5-valid then the following modal propositional calculus argument is S5-valid, call it the “the MPropC argument”: ‘((Cm →
¬Cx), call it the “the MPredC argument”. Aristotle at [30a6–14] gives a proof by ecthesis to show that Bocardo LLL is valid. But using the semantics for the modal system, S5, the translated argument is S5-invalid. For suppose there are only two possible worlds w1 and w2, where each world “sees” each world (including itself). If “the MPredC argument” is S5-valid then the following modal propositional calculus argument is S5-valid, call it the “the MPropC argument”: ‘((Cm →  Bm) ∧ (Cn →
Bm) ∧ (Cn →  Bn)); ((
Bn)); (( Am ∧
Am ∧  ¬Bm) ∨ (
¬Bm) ∨ ( An ∧
An ∧  ¬Bn)); so ((
¬Bn)); so (( Am ∧
Am ∧  ¬Cm ∨ (
¬Cm ∨ ( An ∧
An ∧  ¬Cn))’. But then a countermodel is constructed by: i) letting Am, Bn and Cn be true in world w1; ii) letting Bm, Cm and An be false in w1; iii) letting Am, Cm and Bn be true in world w2; and iv) letting Bm, An and Cn be false in world w2. Then in w1 (Cm →
¬Cn))’. But then a countermodel is constructed by: i) letting Am, Bn and Cn be true in world w1; ii) letting Bm, Cm and An be false in w1; iii) letting Am, Cm and Bn be true in world w2; and iv) letting Bm, An and Cn be false in world w2. Then in w1 (Cm →  Bm) is true, (Cn →
Bm) is true, (Cn →  Bn) is true, (
Bn) is true, ( Am ∧
Am ∧  ¬Bm) is true,
¬Bm) is true,  Am ∧
Am ∧  ¬Cm) is false, and (
¬Cm) is false, and ( An ∧
An ∧  ¬Cn) is false. So “the MPropC argument” is S5-invalid. So “the MPredC argument” is invalid.
¬Cn) is false. So “the MPropC argument” is S5-invalid. So “the MPredC argument” is invalid.
The same countermodel may be used to invalidate the argument that results by replacing the premise ∀x(Cx →  Bx) in “the MPredC” argument with ∀x(Cx →
Bx) in “the MPredC” argument with ∀x(Cx →  Bx).
Bx).
Geach [1964, p. 202] makes the following remarks about McCall’s comments list of seven “Becker-type interpretations”:
Here McCall has not proved what he claims: namely that no Becker-type interpretation will secure simultaneously the validity of Barbara LLL and LXL, the invalidity of Barbara XLL, and the simple conversion of LI propositions (C LIab LIba). For all of these results are obtained if we combine reading (i) of LA from McCall’s list with reading (iii) or equivalently (iv) of LI.
McCall’s list on p. 21 of Becker type interpretations is given on table 3.
Table 3
Seven Becker-type interpretations
| Universal | Particular | |
| (i) | ∀x(Ax →  Bx) Bx) |
∃x(Ax ∧  Bx) Bx) |
| (ii) |  ∀x(Ax → Bx) ∀x(Ax → Bx) |
 ∃x(Ax ∧ Bx) ∃x(Ax ∧ Bx) |
| (iii) | ∀x (Ax → Bx) (Ax → Bx) |
∃x (Ax ∧ Bx) (Ax ∧ Bx) |
| (iv) | ∀x( Ax → Ax →  Bx) Bx) |
∃x( Ax ∧ Ax ∧  Bx) Bx) |
| (v) | ∀x( Ax → Ax →  Bx) Bx) |
∃x( Ax ∧ Ax ∧  Bx) Bx) |
| (vi) | ∀x( Ax → Bx) Ax → Bx) |
∃x( Ax ∧ Ax ∧  Bx) Bx) |
| (vii) | ∀x( Ax → Bx) Ax → Bx) |
∃x( Ax ∧ Bx) Ax ∧ Bx) |
McCall finds interpretations (i) and (ii) in [Becker-Freyseng, 1933], (ii) in [von Wright, 1951], (i) to (v) in [Sugihara, 1957a] and [Sugihara, 1957b], and all but (v) in [Rescher, 1963].
This is what McCall says about these seven interpretations:
None of these interpretations does justice to Aristotle’s system. Not one of them even simultaneously provides for the validity of Barbaras LLL, the invalidity of Barbara XLL, and the convertibility of the particular premise ‘Some A is necessarily B’ into ‘Some B is necessarily A’.
And McCall is correct. Geach is in effect proposing two more interpretations in addition to the seven on the list. Let us call one of them (viii), where LAab is translated as ∀x(Ax →  Bx) and LIab is translated as ∃x
Bx) and LIab is translated as ∃x (Ax ∧ Bx). As Geach says, the other one is essentially the same as it. But interpretation (viii) produces results that are not Aristotelian. For example, if Darii-LXL, valid for Aristotle, is translated using interpretation (viii) the resulting argument is S5-invalid. McCall is looking for an interpretation that provides “100% Aristotelicity”. Geach (p. 202) invites the reader to consider an interpretation of McCall’s LAab and LOab as sentences of an extended assertoric syllogistic, call it the “G-system”, that allows sentences to be formed by using complex terms, terms of form λp (necessarily p) and μp (possibly p), where p is a simple term. McCall’s LAab, LEab, LIab and LOab are translated into the G-system as Aaλb, Eaμb, Iλaλb and Oaμb respectively. Geach (p. 202) says:
(Ax ∧ Bx). As Geach says, the other one is essentially the same as it. But interpretation (viii) produces results that are not Aristotelian. For example, if Darii-LXL, valid for Aristotle, is translated using interpretation (viii) the resulting argument is S5-invalid. McCall is looking for an interpretation that provides “100% Aristotelicity”. Geach (p. 202) invites the reader to consider an interpretation of McCall’s LAab and LOab as sentences of an extended assertoric syllogistic, call it the “G-system”, that allows sentences to be formed by using complex terms, terms of form λp (necessarily p) and μp (possibly p), where p is a simple term. McCall’s LAab, LEab, LIab and LOab are translated into the G-system as Aaλb, Eaμb, Iλaλb and Oaμb respectively. Geach (p. 202) says:
A decision procedure for this calculus can easily be devised: write every formula so that λ-terms and μ-terms appear instead of categoricals prefaced with L, add an antecedent of the form CAλaa [that is, (Aλaa →] for each λ-term and one of the form C Aaμa [that is, (Aaμa →] for each μ-term, and apply Łukasiewicz’s decision procedure for the plain syllogistic to the resulting formula.
So, for example, to determine whether Bocardo LXL (that is, ‘LObc; Aba; so LOac’) is syntactically accepted or syntactically rejected we form the following sentence in the G-system: (Acμc → (Obμc → (Aba → Oaμc))). Following
Łukasiewicz’s decision procedure on pp. 121–126 of [1957], we form an elementary sentence consisting of affirmative simple sentences that is deductively equivalent to it: (Acμc → (Aaμc → (Aba → Abμc))) or (by interchanging terms) (Abμb → (Acμb → (Aac → Aaμb))). The latter sentence fits subcase (d) of the fifth case (p. 124):
The consequent is Aab, and there are antecedents of the type Aaf with f different from a. If there is a chain leading from a to b the expression is asserted on the ground of axiom 3 [our A3, above], the mood Barbara; if there is no such chain, the expression is rejected.
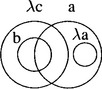
Since a is linked to b by the chain {Aac, Acμb}, (Abμb → (Acμb → (Aac → Aaμb))) is accepted. So Bocardo LXL is accepted in the G-system. But for Aristotle Bocardo LXL is valid.
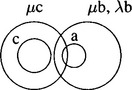
Since questions of validity in the G-system are reduced to questions of validity in the assertoric syllogistic, the familiar Euler diagrams provide a technique for determining whether or not arguments are valid. So, for example, the diagram in figure 1 displays the invalidity of Darii LXL, (LAbc → (Iab → LIac)). Since circle b is included in circle λc, LAbc is true. Since circle a overlaps circle b, Iab is true. Since circle λa does not overlap λc, LIac is false. When constructing such diagrams these conditions must be met: for every term x, the λx circle is included in or equal to the x circle, which is included in or equal to the μx circle. These conditions are natural since whatever is necessarily x is x, and whatever is x is possibly x.
The diagram in figure 2 displays the invalidity of Cesare LLL, (LEcb → (LAab → LEac)). LEcb is true since circle c does not overlap circle μb; LAab is true since circle a is included in circle λb, which is identical to circle μb; and LEac is false since circle a overlaps circle μc.
Geach does not claim that his G-system has “100 percent Aristotelicity”. He says on p. 203 of [1964] that it “can fit in most of Aristotle’s results about syllogisms de necessario”. But table 4 shows that the G-system does not get high marks. “V” occurs in a cell if and only if the relevant syllogism is valid for Aristotle, and “Gc” occurs in a cell if and only if the G-system’s judgment about the acceptance or rejection of the relevant syllogism is in conflict with Aristotle’s. So, for example, the “Gc” in the Darii/LXL cell means that Darii LXL is rejected in the G-system though Aristotle accepts it. The “Gc” in the Bocardo/LXL cell means that Bocardo LXL is accepted in the G-system though Aristotle rejects it. The G-system’s Aristotelicity is ((3 × 14) – 13) ÷ (3 × 14) or about 69%.
Geach’s G-system and Łukasiewicz’s ŁM illustrate two approaches to understanding Aristotle’s work on modal logic. Martha Kneale on p. 91 of [Kneale and Kneale, 1962] poses a dilemma for students of Aristotle given her belief that there are only two approaches to Aristotle’s work.
If modal words modify predicates [Geach’s de re approach is taken], there is no need for a special theory of modal syllogisms. For these are only ordinary assertoric syllogisms of which the premises have peculiar predicates. On the other hand, if modal words modify the whole statements to which they are attached [Łukasiewicz’s de dicto approach is taken], there is no need for a special modal syllogistic since the rules determining the logical relations between modal statements are independent of the character of the propositions governed by the modal words.
McCall agrees with Kneale that the two approaches described above are inadequate. And he devises a third approach that is designed to “catch the fine distinctions Aristotle makes between valid and invalid syllogisms (p. 96)”.
4 Mccall’s L-X-M System
The basis for L-X-M includes that of ŁA together with the following primitive symbols, formation rules, definitions, axioms and transformation rules. Only some of the rejection axioms are given here. The partial list is big enough to illustrate how rejection deductions are constructed in L-X-M. For the full list of rejection axioms see [McCall, 1963] or [Johnson, 1989].
Formation rules
| FR1’ | If Qu is a quantifier and x and y are term variables then Quxy is a categorical expression. |
| FR2’ | If p is a categorical expression then ¬p is a categorical expression and Lp is a wff. |
| FR3’ | Categorical expressions are wffs. |
| FR4’ | If p and q are wffs then ¬p and (p → q) are wffs. |
| FR5’ | The only wffs are those in virtue of FR1’ to FR4’. |
So, for example, Aab is a categorical expression by FR1’, so ¬Aab is a categorical expression by FR2’, so ¬¬Aab is a categorical expression by FR2’, so L¬¬Aab is a wff by FR2’, so ¬L¬¬Aab is a wff by FR4’. Note that LLAab is not a wff.
Assertion axioms
Use A0, A1, A3 and A4 from system ŁA. Change A2 for ŁA from  Iaa to
Iaa to  LIaa. Then add the following axioms.
LIaa. Then add the following axioms.
| A5 (Barbara LXL) |  (LAbc → (Aab → LAac)) (LAbc → (Aab → LAac)) |
| A6 (Cesare LXL) |  (LEcb → (Aab → LEac)) (LEcb → (Aab → LEac)) |
| A7 (Darii LXL) |  (LAbc → (Iab → LIac)) (LAbc → (Iab → LIac)) |
| A8 (Ferio LXL) |  (LEbc → (Iab → LOac)) (LEbc → (Iab → LOac)) |
| A9 (Baroco LLL) |  (LAcb → (LOeb → LOac)) (LAcb → (LOeb → LOac)) |
| A10 (Bocardo LLL) |  (LObc → (LAba → LOac)) (LObc → (LAba → LOac)) |
| A11 (LI conversion) |  (LIab → LIba) (LIab → LIba) |
| A12 (LA subordination) |  (LAab → Aab) (LAab → Aab) |
| A13 (LI subordination) |  (LIab → Iab) (LIab → Iab) |
| A14 (LO subordination) |  (LOab → Oab) (LOab → Oab) |
Assertion transformation rules
Use the assertion transformation rules AR1 to AR3 from ŁA and add the following rule.
| AR4 | (Assertions involving doubly negated categorical expressions, DN) From  (…p…) infer (…p…) infer  (…¬¬p…) and vice versa, if p is a categorical expression. (So, for example, from (…¬¬p…) and vice versa, if p is a categorical expression. (So, for example, from  (LAab → LAab) infer (LAab → LAab) infer  (LAab → L¬¬Aab) by DN. By using SE we may infer that (LAab → L¬¬Aab) by DN. By using SE we may infer that  (LAab → ¬¬LAab) given (LAab → ¬¬LAab) given  (LAab → LAab).) (LAab → LAab).) |
Rejection axioms
Use R1 from system ŁA and add the following rejection axioms.
 (LAaa →(LAcc →(MAac →(LAca →Aac))))15
(LAaa →(LAcc →(MAac →(LAca →Aac))))15
Page references are to McCall’s [1963]. McCall uses asterisks to refer to rejections.
Rejection transformation rules
Use rejection transformation rules R1–R4 as well as the following rule.
| R5 | (Rejections involving doubly negated categorical expressions, R-DN) From  (…p…) infer (…p…) infer  (…¬¬p…) and vice versa, if p is a categorical expression. (So, for example, from (…¬¬p…) and vice versa, if p is a categorical expression. (So, for example, from  L¬¬Iab infer L¬¬Iab infer  LIab.) LIab.) |
We imitate the discussion of Łukasiewicz’s ŁA system by proving various “immediate inferences”. Oppositions, conversions, subalternations and subordinations are listed.
Theorem 4.1: (Apodeictic oppositions, Ap-opp) i)  (¬LAab ↔ MOab); ii)
(¬LAab ↔ MOab); ii)  (¬MOab ↔ LAab); iii)
(¬MOab ↔ LAab); iii)  (¬LEab ↔ MIab); iv)
(¬LEab ↔ MIab); iv)  (¬MIab ↔ LEab); v)
(¬MIab ↔ LEab); v)  (¬LIab ↔ MEab); vi)
(¬LIab ↔ MEab); vi)  (¬MEab ↔ LIab); vii)
(¬MEab ↔ LIab); vii)  (¬LOab ↔ MAab); and viii)
(¬LOab ↔ MAab); and viii)  (¬MAab ↔ LOab).
(¬MAab ↔ LOab).
2.  (¬LAab ↔ ¬L¬¬Aab) (from 1 by DN)
(¬LAab ↔ ¬L¬¬Aab) (from 1 by DN)
3.  (¬LAab ↔ MOab) (i, from 2 by DDI, given Def M and Def O)
(¬LAab ↔ MOab) (i, from 2 by DDI, given Def M and Def O)
4.  (¬MOab ↔ ¬¬LAab) (from 3 by RV)
(¬MOab ↔ ¬¬LAab) (from 3 by RV)
6.  (¬MOab ↔ LAab) (ii, from 4 and 5 by SE)
(¬MOab ↔ LAab) (ii, from 4 and 5 by SE)
8.  (¬LEab ↔ ¬L¬¬Eab) (from 7 by DN)
(¬LEab ↔ ¬L¬¬Eab) (from 7 by DN)
9.  (¬LEab ↔ ¬L¬¬¬Iab) (from 8 by DDI, given Def E)
(¬LEab ↔ ¬L¬¬¬Iab) (from 8 by DDI, given Def E)
10.  (¬LEab ↔ ¬L¬Iab) (from 9 by DN)
(¬LEab ↔ ¬L¬Iab) (from 9 by DN)
11.  (¬LEab ↔ MIab) (iii, from 10 by DDI, given Def M)
(¬LEab ↔ MIab) (iii, from 10 by DDI, given Def M)
Use similar reasoning for the other four asserted biconditionals.
Theorem 4.2: (Apodeictic conversions, Ap-con) i)  (LEab → LEba); ii)
(LEab → LEba); ii)  (LIab → LIba); iii)
(LIab → LIba); iii)  (MEab → MEba); and iv)
(MEab → MEba); and iv)  (MIab → MIba).
(MIab → MIba).
Theorem 4.3: (Apodeictic subalternations, Ap-sub-a) i)  (LAab → LIab); ii)
(LAab → LIab); ii)  (LEab → LOab); iii)
(LEab → LOab); iii)  (MAab → mIab); and iv)
(MAab → mIab); and iv)  (MEab → MOab).
(MEab → MOab).
Theorem 4.4: (Apodeictic conversions per accidens, Ap-con(pa)) i)  (LAab → LIba); ii)
(LAab → LIba); ii)  (MAab → MIba); iii)
(MAab → MIba); iii)  (LEab → LOba); and iv)
(LEab → LOba); and iv)  (MEab → MOba).
(MEab → MOba).
Theorem 4.5: (Subordinations, Sub-o) i)  (LAab → Aab); ii)
(LAab → Aab); ii)  (Aab → MAab); iii)
(Aab → MAab); iii)  (LEab → Eab); iv)
(LEab → Eab); iv)  (Eab → MEab); v)
(Eab → MEab); v)  (LIab → Iab); vi)
(LIab → Iab); vi)  (Iab → MIab); vii)
(Iab → MIab); vii)  (LOab → Oab); and viii)
(LOab → Oab); and viii)  (Oab → MOab).
(Oab → MOab).
2.  (Aab → MAab) (ii, from 1 by RV, SE)
(Aab → MAab) (ii, from 1 by RV, SE)
3.  (Aaa → MAaa) (from 2 by US)
(Aaa → MAaa) (from 2 by US)
6.  (LEbc → (Iab → LOac)) (by A8)
(LEbc → (Iab → LOac)) (by A8)
7.  (MAac → (Iab → MIbc)) (from 6 by RV, SE)
(MAac → (Iab → MIbc)) (from 6 by RV, SE)
8.  (MAaa → (Iab → MIba)) (from 7 by US)
(MAaa → (Iab → MIba)) (from 7 by US)
9.  (Iab → MIba) (from 5 and 8 by MP)
(Iab → MIba) (from 5 and 8 by MP)
10.  (MIba → MIab) (by Ap-con, US)
(MIba → MIab) (by Ap-con, US)
Proofs of the other four subordinations are straightforward and are omitted.
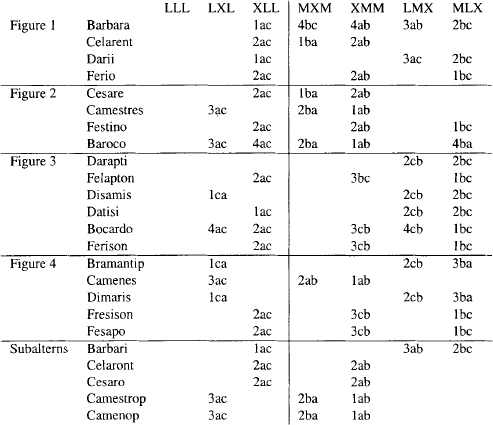
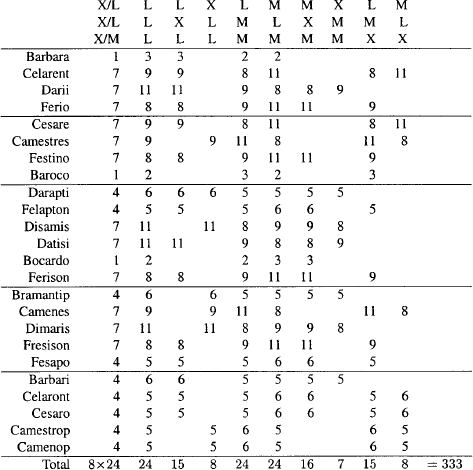
We show that all of the entries marked with ‘V’ on table 4 and all of the entries marked with a blank on table 5 correspond to asserted wffs in L-X-M. Proofs are streamlined by assuming immediate inferences established above and any immediate inferences obtainable from them by US. So, for example, in the proof of Barbari LXL from Barbara LXL by CW in theorem LXL the subalternation  (LAac → LIac) is assumed.
(LAac → LIac) is assumed.
Theorem 4.6: All unmarked LXL and XLL cells on table 5 represent asserted wffs.
1.  (LAbc → (Aab → LAac)) (Barbara LXL, by A5)
(LAbc → (Aab → LAac)) (Barbara LXL, by A5)
2.  (LAbc → (Aab → LIac)) (Barbari LXL, from 1 by CW)
(LAbc → (Aab → LIac)) (Barbari LXL, from 1 by CW)
3.  (Acb → (LAba → LIac)) (Bramantip XLL, from 2 by AI, CW, US)
(Acb → (LAba → LIac)) (Bramantip XLL, from 2 by AI, CW, US)
4.  (LAbc → (Iab → LIac)) (Darii LXL, by A7)
(LAbc → (Iab → LIac)) (Darii LXL, by A7)
5.  (LAbc → (Iba → LIac)) (Datisi LXL, from 4 by AS)
(LAbc → (Iba → LIac)) (Datisi LXL, from 4 by AS)
6.  (LAbc → (Aba → LIac)) (Darapti LXL, from 5 by AS)
(LAbc → (Aba → LIac)) (Darapti LXL, from 5 by AS)
7.  (Ibc → (LAab → LIac)) (Disamis XLL, from 5 by AI, CW, US)
(Ibc → (LAab → LIac)) (Disamis XLL, from 5 by AI, CW, US)
8.  (Icb → (LAba → LIac)) (Dimaris XLL, from 4 by AI, CW, US)
(Icb → (LAba → LIac)) (Dimaris XLL, from 4 by AI, CW, US)
9.  (Acb → (LAba → LIac)) (Darapti XLL, from 7 by AS)
(Acb → (LAba → LIac)) (Darapti XLL, from 7 by AS)
10.  (LEbc → (Iab → LOac)) (Ferio LXL, by A8)
(LEbc → (Iab → LOac)) (Ferio LXL, by A8)
11.  (LEcb → (Iab → LOac)) (Festino LXL, from 9 by AS)
(LEcb → (Iab → LOac)) (Festino LXL, from 9 by AS)
12.  (LEbc → (Iba → LOac)) (Ferison LXL, from 9 by AS)
(LEbc → (Iba → LOac)) (Ferison LXL, from 9 by AS)
13.  (LEbc → (Aba → LOac)) (Felapton LXL, from 11 by AS)
(LEbc → (Aba → LOac)) (Felapton LXL, from 11 by AS)
14.  (LEcb → (Iba → LOac)) (Fresison LXL, from 9 by AS)
(LEcb → (Iba → LOac)) (Fresison LXL, from 9 by AS)
15.  (LEcb → (Aba → LOac)) (Fesapo LXL, from 13 by AS)
(LEcb → (Aba → LOac)) (Fesapo LXL, from 13 by AS)
16.  (LEcb → (Aab → LEac)) (Cesare LXL, by A6)
(LEcb → (Aab → LEac)) (Cesare LXL, by A6)
17.  (LEbc → (Aab → LEac)) (Celarent LXL, from 15 by AS)
(LEbc → (Aab → LEac)) (Celarent LXL, from 15 by AS)
18.  (Acb → (LEab → LEac)) (Camestres XLL, from 16 by AI, CW, US)
(Acb → (LEab → LEac)) (Camestres XLL, from 16 by AI, CW, US)
19.  (Acb → (LEba → LEac)) (Camenes XLL, from 17 by AS)
(Acb → (LEba → LEac)) (Camenes XLL, from 17 by AS)
20.  (LEbc → (Aab → LEac)) (Celaront LXL, from 16 by CW)
(LEbc → (Aab → LEac)) (Celaront LXL, from 16 by CW)
21.  (LEcb → (Aab → LOac)) (Cesaro LXL, from 15 by CW)
(LEcb → (Aab → LOac)) (Cesaro LXL, from 15 by CW)
Theorem 4.7: All unmarked LLL cells on table 5 represent asserted wffs.
Proof: Use A9, A10 and AS with theorem 4.6. So, for example, Barbara LLL is asserted, since Barbara LXL is asserted and  (LAab → Aab). Disamis LLL is assserted, since Disamis XLL is asserted and
(LAab → Aab). Disamis LLL is assserted, since Disamis XLL is asserted and  (LIab → Iab).
(LIab → Iab).
Theorem 4.8: All unmarked MXM, XMM, LMX and MLX cells on table 5 represent asserted wffs.
Proof: Use theorem 4.6 and RV. So, for example, the assertion of Darii MXM is generated from the assertion of Ferison LXL as follows.  (MAbc → (Iab → MIac)) since
(MAbc → (Iab → MIac)) since  (LEac → (Iab → LObc)) (by RV and SE), since
(LEac → (Iab → LObc)) (by RV and SE), since  (LEbc → (Iba → LOac)) (by US). The assertion of Festino LMX is generated from the assertion of Celarent LXL as follows.
(LEbc → (Iba → LOac)) (by US). The assertion of Festino LMX is generated from the assertion of Celarent LXL as follows.  (LEcb → (MIab → Oac)) since
(LEcb → (MIab → Oac)) since  (LEcb → (Aac → LEab)) (by RV and SE), since
(LEcb → (Aac → LEab)) (by RV and SE), since  (LEbc → (Aab → LEac)) (by US). The assertion of Camenes MLX is generated from the assertion of Fresison LXL as follows.
(LEbc → (Aab → LEac)) (by US). The assertion of Camenes MLX is generated from the assertion of Fresison LXL as follows.  (MAcb → (LEba → Eac)), since
(MAcb → (LEba → Eac)), since  (Iac → (LEba → LOcb)) (by RV and SE), since
(Iac → (LEba → LOcb)) (by RV and SE), since  (LEba → (Iac → LOcb)) (by AI), since (LEcb → (Iba → LOac)) (by US).
(LEba → (Iac → LOcb)) (by AI), since (LEcb → (Iba → LOac)) (by US).
4.1 Rejections in L-X-M
To reject the syllogisms not marked with a “V” on table 4, as well as other invalid inferences, McCall adds twelve rejection axioms to the list of rejection axioms for the ŁA-system. We shall illustrate how some of these rejection axioms are used to reject some wffs.
Proof: Recall that R2 =  σ, where σ = (LAbb → (MAab → (Aac → (LAca → (LAbc → LAac))))).
σ, where σ = (LAbb → (MAab → (Aac → (LAca → (LAbc → LAac))))).
2.  ((Aac → (LAca → LAac)) → σ) (by A0)
((Aac → (LAca → LAac)) → σ) (by A0)
3.  (Aac → (LAca → LAac)) (from 1 and 2 by R-D)
(Aac → (LAca → LAac)) (from 1 and 2 by R-D)
4.  (Aac → (LAca → LAaa)) (by A5 and US)
(Aac → (LAca → LAaa)) (by A5 and US)
5.  ((Aac → (LAca → LAaa)) → ((Aac → (LAaa → LAac)) → (Aac → (LAca → LAac)))) (by A0)
((Aac → (LAca → LAaa)) → ((Aac → (LAaa → LAac)) → (Aac → (LAca → LAac)))) (by A0)
6.  ((Aac → (LAaa → LAac)) → (Aac → (LAca → LAac))) (from 4 and 5 by MP)
((Aac → (LAaa → LAac)) → (Aac → (LAca → LAac))) (from 4 and 5 by MP)
1.  (Abc → (LAab → LAac)) (by theorem 4.9)
(Abc → (LAab → LAac)) (by theorem 4.9)
2.  (Abc → (MOac → MOab)) (from 1 by theorem R-RV and R-SE)
(Abc → (MOac → MOab)) (from 1 by theorem R-RV and R-SE)
3.  (Acb → (MOab → MOac)) (Baroco XMM, from 2 by R-US)
(Acb → (MOab → MOac)) (Baroco XMM, from 2 by R-US)
Proof: Recall that R3 =  σ, where σ is (LAaa → (LAcc → (MAac → (LAca → Aac)))).
σ, where σ is (LAaa → (LAcc → (MAac → (LAca → Aac)))).
Proof: Recall that R4 =  σ, where σ = (LAaa →(LAbb →(LAcc →LAab →(MAba →(MAbc →(LAcb →Iac)))))).
σ, where σ = (LAaa →(LAbb →(LAcc →LAab →(MAba →(MAbc →(LAcb →Iac)))))).
2.  ((MAbc → (LAab → Iac)) → σ) (by A0)
((MAbc → (LAab → Iac)) → σ) (by A0)
3.  (MAbc → (LAab → Iac)) (Barbari MLX, from 1 and 2 by R-US)
(MAbc → (LAab → Iac)) (Barbari MLX, from 1 and 2 by R-US)
4.  (LAab → (MAbc → Iac)) (from 3 by R-AI)
(LAab → (MAbc → Iac)) (from 3 by R-AI)
6.  (LAab → (MAbc → Ica)) (from 4 and 5 by R-CS)
(LAab → (MAbc → Ica)) (from 4 and 5 by R-CS)
7.  (LAcb → (MAba → Iac)) (Bramantip LMX, from 6 by R-US)
(LAcb → (MAba → Iac)) (Bramantip LMX, from 6 by R-US)
8.  (Eac → (LAab → LObc)) (from 3 by R-RV and SE)
(Eac → (LAab → LObc)) (from 3 by R-RV and SE)
9.  (Ebc → (LAba → LOac)) (Felapton XLL, from 8 by R-US)
(Ebc → (LAba → LOac)) (Felapton XLL, from 8 by R-US)
Our purpose in this section has been to illustrate how McCall’s rejection apparatus works. In the next section we discuss this result: whatever is rejected by using McCall’s rejection apparatus may be shown invalid by using countermodels. McCall’s [1963] contains no discussion of models.
5 Semantics for L-X-M
In [Johnson, 1989] a semantics for McCall’s L-X-M is given. Validity is defined by using models, asserted wffs in L-X-M are shown to be valid (that is, system L-X-M is sound), and rejected sentences are shown to be invalid. So valid wffs in X-L-M are shown to be accepted (that is, system L-X-M is complete) since, as McCall shows, every wff in L-X-M is either accepted or rejected. The presentation of the semantics here will benefit from comments about it in Thom’s [1996] and Thomason’s [1993] and [1997].16
The semantics for L-X-M extends the familiar semantics for the assertoric syllogistic that assigns non-empty sets of objects to terms. To define the semantic notion of validity we refer to models and valuations relative to models.
Definition 5.1: (model)  is a model iff
is a model iff  = 〈W, n+, q+, n−, q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”, where +(x) is short for n+(x)∪q+(x), and x
= 〈W, n+, q+, n−, q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”, where +(x) is short for n+(x)∪q+(x), and x  y (x overlaps y) is short for x ∩ y ≠ Ø:
y (x overlaps y) is short for x ∩ y ≠ Ø:
| B1 | If f and g are any of the functions n+, q+, q− or n− and f ≠ g, then, for every term x, f (x) ∩ g(x) = Ø and for every x, n+ (x) ∪ q+ (x) ∪ q− (x) ∪ n− (x) = W |
| B2 | For every x, n+ (x) ≠ Ø |
| B3 | (Forevery x, y and z) if + (z) ⊆ n− (y) and + (x) ⊆ + (y) then + (x) ⊆ n− (z) |
| B4 | If + (y) ⊆ n + (z) and + (x)  + (y) then n+ (x) + (y) then n+ (x)  n+ (z) n+ (z) |
| B5 | If + (y) ⊆ n− (z) and + (x)  + (y) then n+ (x) + (y) then n+ (x)  n− (z) n− (z) |
| B6 | If + (z) ⊆ n+ (y) and n+ (x)  n− (y) then n+ (x) n− (y) then n+ (x)  n− (z) n− (z) |
For an intuitive grasp of the notion of a model think of W as the world, n+ (a) as the set of things in W that are essentially a, q+ (a) as the set of things in W that are contingently a and are a, n− (x) as the set of things in W that are essentially non-a, and q− (a) as the set of things in W that are contingently not a and are not a.
Definition 5.2: (valuation) A valuation V is a function that assigns t or f, but not both, to sentences, where: i) V(¬p) = t iff V(p) = f; and ii) V(p → q) = t iff V(¬p) = t or V(q) = f; and iii) V(L¬¬p) = t iff V(Lp) = t.
Definition 5.3: (valuation relative to model M) Let VM, a valuation relative to a model M, be a valuation that satisfies the following “superstructural conditions”:
| S1 | (For every x and y) VM(Axy) t iff + (x) ⊆ +(y) |
| S2 | VM(Ixy) = t iff + (x)  + (y) + (y) |
| S3 | VM (LAxy) = t iff + (x) ⊆ n+ (y) |
| S4 | VM (LIxy) = t iff n+ (x)  n+ (y) n+ (y) |
| S5 | VM (L¬Axy) = t iff n+ (x)  n− (y) n− (y) |
| S6 | VM (L¬Ixy) = t iff + (x) ⊆ n− (y) |
Definition 5.4: (valid) Let σ be an L-X-M sentence. σ is valid (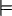 σ) iff, for every model M, every valuation relative to M assigns t to σ. σ is invalid iff σ is not valid.
σ) iff, for every model M, every valuation relative to M assigns t to σ. σ is invalid iff σ is not valid.
In this section we shall construct models that show the invalidity of all of the syllogisms that correspond to marked cells on table 5. Exactly four models suffice to show the invalidity of the invalid LXL and XLL models marked on these tables. Models constructed by interchanging rows in these four models suffice to invalidate the remaining invalid syllogisms mentioned on the table.
Table 5 agrees with table 7 on p. 43 of [McCall, 1963]. A cell on the former is marked if and only if it is unmarked on the latter. The marks on McCall’s table indicate the relevant syllogism is syntactically asserted in L-X-M. McCall’s discussion of L-X-M is totally syntactic. He gives no formal semantics and thus no formal definition of validity. But as shown in [1989], the syllogisms that are syntactically asserted in L-X-M are the syllogisms that are valid in L-X-M and vice versa. The above theorems 4.6 and 4.7 pertain to the unmarked cells on table 5.
We begin by constructing a model  1, presented by table 6, that shows the invalidity of Barbara LXL. When giving such tables we use the following conventions: set brackets are omitted when giving the range of a function, a blank cell indicates the range of the relevant function is the empty set, for terms x other than those explicitly mentioned on the table, n+(x) = n+ (a), q+ (x) = q+ (a), n− (x) = n− (a) and q− (x) = q− (a), and W = n+ (a) ∪ q+ (a) ∪ n− (a) ∪ q− (a).
1, presented by table 6, that shows the invalidity of Barbara LXL. When giving such tables we use the following conventions: set brackets are omitted when giving the range of a function, a blank cell indicates the range of the relevant function is the empty set, for terms x other than those explicitly mentioned on the table, n+(x) = n+ (a), q+ (x) = q+ (a), n− (x) = n− (a) and q− (x) = q− (a), and W = n+ (a) ∪ q+ (a) ∪ n− (a) ∪ q− (a).
So, for example, given table 6 the set of things that are essentially a has only one member, namely 1. The set of things that are c and are contingently c has two members: 1 and 2. The set of things that are essentially not b has no members. And the set of things that are not d and are contingently not d has 3 as its only member. W = {1, 2, 3}.
Table 6 expresses a model. Base conditions B1 and B2, here and below, do not require a comment. B3, B5 and B6 are trivially satisfied since, for every x and y, + (x)∩n− (y) = Ø. Suppose (y) ⊆ n+(z). Then z = b. For all x, n+(x)  n+(b). So B4 is satisfied.
n+(b). So B4 is satisfied.
Given model  1: i) V
1: i) V 1 (Abc) = t since +(b) ⊆ +(c); ii) VM1 (LAab) = t since + (a) ⊆ n+ (b); and iii) V
1 (Abc) = t since +(b) ⊆ +(c); ii) VM1 (LAab) = t since + (a) ⊆ n+ (b); and iii) V 1 (LAac) = f since +(a)
1 (LAac) = f since +(a)  n+(c). So V
n+(c). So V 1 (Abc → (LAaB → LAac)) = f. So
1 (Abc → (LAaB → LAac)) = f. So 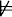 (Abc → (LAab → LAac)). So Barbara XLL is invalid. The invalidity of Barbara XLL is marked on table 5 by putting ‘1ac’ in the Barabara/XLL cell.
(Abc → (LAab → LAac)). So Barbara XLL is invalid. The invalidity of Barbara XLL is marked on table 5 by putting ‘1ac’ in the Barabara/XLL cell.
Aristotle’s informal counterexample for Barbara XLL at 30a28–30 uses terms ‘motion’, ‘animal’ and ‘man’. For Aristotle, Barbara XLL, construed as an inferential syllogism, is invalid given the inference ‘All animals are (accidentally) in motion; all men are necessarily animal; so all men are necessarily in motion’. Aristotle takes the premises to be true and the conclusion false, making Barbara XLL invalid.
By interchanging rows a and b in table 6 we may construct a model  1bc expressed by table 7 that shows that Ferio MLX invalid.
1bc expressed by table 7 that shows that Ferio MLX invalid.
In general, if a table satisfies conditions B1 to B6. so will a table that results from the interchanging of its rows. For none of these conditions requires a particular ordering of rows. Note that V 1bc (MEac) = t, V
1bc (MEac) = t, V 1bc (LIab) = t and V
1bc (LIab) = t and V 1bc (Obc) = f. So
1bc (Obc) = f. So 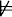 (MEac → (Llab → Oac)). That is, Ferio MLX is invalid.
(MEac → (Llab → Oac)). That is, Ferio MLX is invalid.
This is the recipe for constructing a table T2 for model  Nzxy (where x and y are a, b or c) from a table T1 for model
Nzxy (where x and y are a, b or c) from a table T1 for model  N (where T1 has rows a, b and c): make row a in T1 be row x in T2, make row c in T1 be row y in T2, and make row b in T1 be the third row in T2. Every row in T2 must be an a-row, a b-row or a c-row. So, for example, consider the Baroco/XMM cell on table 5, which is marked with ‘lab’. Use the recipe to construct table 8 for model
N (where T1 has rows a, b and c): make row a in T1 be row x in T2, make row c in T1 be row y in T2, and make row b in T1 be the third row in T2. Every row in T2 must be an a-row, a b-row or a c-row. So, for example, consider the Baroco/XMM cell on table 5, which is marked with ‘lab’. Use the recipe to construct table 8 for model  1ab, which invalidates Baroco XMM. (The a-row of table 6 becomes the a-row of table 8; the c-row of 6 becomes the b-row of table 8; and the b-row of 6 becomes the c-row of table 8.) Since
1ab, which invalidates Baroco XMM. (The a-row of table 6 becomes the a-row of table 8; the c-row of 6 becomes the b-row of table 8; and the b-row of 6 becomes the c-row of table 8.) Since  1ab (Acb) = t,
1ab (Acb) = t,  1ab (MOab) = t and
1ab (MOab) = t and  1ab (MOac) = f,
1ab (MOac) = f, 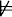 (Acb → (MOab → MOac)).
(Acb → (MOab → MOac)).
Model  2 expressed by table 9 may be used to show that Celarent XLL is invalid.
2 expressed by table 9 may be used to show that Celarent XLL is invalid.
Table 9 expresses a model. For all x and y, +x  n− (y). So conditions B3 and B5 are trivially satisfied. For all x and y if +(x)
n− (y). So conditions B3 and B5 are trivially satisfied. For all x and y if +(x)  +(y) then n+(x)
+(y) then n+(x)  +(y). So B4 is satisfied. For all x and y, if +(x) ⊆ n+(y) then n−(y) ⊆ n− (x). So B6 is satisfied.
+(y). So B4 is satisfied. For all x and y, if +(x) ⊆ n+(y) then n−(y) ⊆ n− (x). So B6 is satisfied.
Celarent XLL is invalid since: i) V 2 (Ebc) = t since +(b) does not overlap +(c); ii) V
2 (Ebc) = t since +(b) does not overlap +(c); ii) V 2 (LAab) = t since +(a) ⊆ n+(b); and iii) V
2 (LAab) = t since +(a) ⊆ n+(b); and iii) V 2 (LEac) = f since +(a)
2 (LEac) = f since +(a)  n−(c). So V
n−(c). So V 2 (Ebc → (LAab → LEac)) = f. So
2 (Ebc → (LAab → LEac)) = f. So 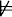 (Ebc → (LAab → LEac)).
(Ebc → (LAab → LEac)).
Model  3 expressed by table 10 may be used to show that Camestres LXL is invalid.
3 expressed by table 10 may be used to show that Camestres LXL is invalid.
Table 10 expresses a model. B3 and B5 are trivially satisfied since, for every x and y, + (x)  n−(y). For B4 note that if +(x)
n−(y). For B4 note that if +(x)  +(y) then n+(x)
+(y) then n+(x)  +(y). For B6 note that if + (z) ⊆ n+(y) then n−(y) ⊆ n−(z).
+(y). For B6 note that if + (z) ⊆ n+(y) then n−(y) ⊆ n−(z).
Camestres LXL is invalid since: i) V 3 (LAcb) = t since + (c) ⊆ n+(b); ii) V
3 (LAcb) = t since + (c) ⊆ n+(b); ii) V 3 (Eab) = t since + (a)∩+(b) = Ø and iii) V
3 (Eab) = t since + (a)∩+(b) = Ø and iii) V 3 (LEac) = f since + (a)
3 (LEac) = f since + (a)  n− (c). So V
n− (c). So V 3 (LAcb → (Eab → LEac) = f. So
3 (LAcb → (Eab → LEac) = f. So 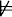 (LAcb → (Eab → LEac)).
(LAcb → (Eab → LEac)).
For Aristotle, Camestres LXL is invalid since Celarent XLL is invalid. A “semantic rule” that underwrites this reduction of an invalidity to an invalidity may be stated as follows.
is the semantic counterpart of the syntactic rule R-DR3, which is called rejection by antecedent weakening (R-AW). Given the rejection of Celarent XLL (Ebc → (LAab → LIac)) and the conversion principle  (Ebc → Ecb), Camestres LXL is rejected by R-AW. Likewise, given the invalidity of Celarent XLL and the semantic conversion principle
(Ebc → Ecb), Camestres LXL is rejected by R-AW. Likewise, given the invalidity of Celarent XLL and the semantic conversion principle  (Ebc → Ecb), Camestres LXL is invalid by R
(Ebc → Ecb), Camestres LXL is invalid by R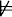 -AW.
-AW.
Semantic counterparts of other syntactic rejection rules may be put to use to establish invalidities. We illustrate this point by considering the semantic counterpart of R-RV.
By R -RV, since
-RV, since 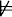 (Ebc → (LAab → LEac)) (Celarent XLL is invalid),
(Ebc → (LAab → LEac)) (Celarent XLL is invalid), 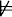 (Ebc → (¬LEac → ¬LAab)). By using semantic counterparts of other syntactic principles stated above it is easy to conclude that Festino XMM is invalid.
(Ebc → (¬LEac → ¬LAab)). By using semantic counterparts of other syntactic principles stated above it is easy to conclude that Festino XMM is invalid.
To show that Baroco XLL is invalid we use model  4, presented on table 11.17
4, presented on table 11.17
Table 11 expresses a model. Base conditions B3 and B5 are trivially satisfied since, for every x and y, +(x)  n−(y). B4 and B6 are trivially satisfied since, for every x and y, n+(x)
n−(y). B4 and B6 are trivially satisfied since, for every x and y, n+(x)  n+(y).
n+(y).
Given model  4: i) V
4: i) V 4 (Acb) = t since +(c) ⊆ +(b); ii) V
4 (Acb) = t since +(c) ⊆ +(b); ii) V 4 (LOab) = t since n+(a)
4 (LOab) = t since n+(a)  n−b; and iii) V
n−b; and iii) V 4 (LOac) = f since n+(a) does not overlap n−(c). So V
4 (LOac) = f since n+(a) does not overlap n−(c). So V 4 ((Acb → (LOab → LOac))) = f. So
4 ((Acb → (LOab → LOac))) = f. So 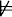 (Acb → (LOab → LOac)). Following the pattern indicated above we record on table 5 the invalidity of Baroco XLL by putting ‘4ac’ in the Baroco/XLL cell, where ‘4’ refers to model
(Acb → (LOab → LOac)). Following the pattern indicated above we record on table 5 the invalidity of Baroco XLL by putting ‘4ac’ in the Baroco/XLL cell, where ‘4’ refers to model  4 and ‘ac’ indicates that ‘a’ and ‘c’ are taken as minor and major terms, respectively.
4 and ‘ac’ indicates that ‘a’ and ‘c’ are taken as minor and major terms, respectively.
Aristotle’s counterexample for Baroco XLL is controversial. According to Thom on p. 148 of [1991] Aristotle used terms ‘animal’, ‘man’ and ‘white’, generating the purported counterexample: ‘All men are animals; some whites are necessarily not animals; so some whites are necessarily not men.’ Thom says:
The problem with this counter-example is not (as van Rijen supposes [1989]) that the major premise is necessarily true. It is that, if the minor is taken to be true then the conclusion will be true also.
In agreement with Thom, Aristotle did not provide a good counterexample for Baroco XLL. A better informal counterexample is found in [Johnson, 1993, p. 179]: ‘All things that are chewing are bears (Acb); some animals (dogs, say) are necessarily not bears (LOab); so some animals are necessarily not chewing (LOac)’. We do not follow Thom in developing formal systems that take Baroco XLL to be invalid.
Though models  1 to
1 to  4 and variants of them constructed by interchanging rows in them suffice to give countermodels for the invalid syllogisms marked on table 5, other models are needed to invalidate all of McCall’s rejection axioms and thus all of the invalid wffs. The model used in [1989] to invalidate McCall’s (LAbb →(LAff →(Aad →(LAda →(MAae →(LAcb →(LAbd →(LAce →(Aec →(LAfc →(MAdf →MAac))))))))))) (*5.41 on p. 59) has four members. It is presented on table 12.
4 and variants of them constructed by interchanging rows in them suffice to give countermodels for the invalid syllogisms marked on table 5, other models are needed to invalidate all of McCall’s rejection axioms and thus all of the invalid wffs. The model used in [1989] to invalidate McCall’s (LAbb →(LAff →(Aad →(LAda →(MAae →(LAcb →(LAbd →(LAce →(Aec →(LAfc →(MAdf →MAac))))))))))) (*5.41 on p. 59) has four members. It is presented on table 12.
An implication of [Johnson, 1989] is that every invalid L-X-M wff of form (p1 → (p2 → … → pn) …), where each pi (for 1 ≤ i ≤ n) is a simple wff or the negation of a simple wff, may be shown invalid by using a model 〈W,…〉 in which W has no more than 6 members.18
In the next section we shall examine valuable attempts by Thomason to improve on the semantics discussed in this section.
5.1 Thomason models
In [Thomason, 1993] three notions of models are defined that enable Thomason to obtain soundness and completeness results for McCall’s L-X-M calculus. In contrast to the soundness and completeness proofs given in [Johnson, 1989] no use is made of rejection axioms and rejection rules. One of these models comes close to the notion of a model defined above. We call it a “T3-model” (his “model3”) and define it as follows.
Definition 5.5: (T3-model)  is a T3-model iff
is a T3-model iff  = 〈W, n+, q+, n−, q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”, where + (x) is short for n+ (x) ∪ q+ (x):
= 〈W, n+, q+, n−, q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”, where + (x) is short for n+ (x) ∪ q+ (x):
| B1 | If f and g are any of the functions n+, q+, q− or n− and f ≠ g, then, for every term x, f(x) ∩ g(x) = Ø and for every x, n+(x) ∪ q+(x) ∪ q−(x) ∪ n−(x) = W |
| B2 | For every x, n+ (x) ≠ Ø |
| BT3 | (For every x and y) if + (x)  + (y) then +(x) + (y) then +(x)  n+ (y) n+ (y) |
| BT4 | If + (x) ⊆ n−(y) then+(y) ⊆ n−(x) |
| BT5 | If + (x) ⊆ n+(y) then n−(y) ⊆ n−(x) |
To define “valuation relative to a model” and “validity” Thomason uses the same superstructural conditions as used above.
Thomason, on p. 133 of [1997], says that in his [1993] he “tried to find simpler, and apparently weaker, requirements for models” than those given in [Johnson, 1989]. In the motivating section of [Thomason, 1993] he says “Johnson … provided a semantics that has the right validities, but the latter is in some sense contrived.” No doubt conditions BT3, BT4 and BT5 are more easily understood than B3, B4, B5 and B6 but Thomason is not correct in saying that the former, taken collectively, are weaker than the latter, taken collectively. We use the following theorem to show the relationship between T3-models and “J-models”, the models defined above that satisfy base conditions B1 to B6.
Proof: For i) suppose  is a T3-model. First, suppose + (z) ⊆ n−(y) and +(x) ⊆ +(y). Then, by BT4, +(y) ⊆ n−(z). Then +(x) ⊆ n−(z). Then
is a T3-model. First, suppose + (z) ⊆ n−(y) and +(x) ⊆ +(y). Then, by BT4, +(y) ⊆ n−(z). Then +(x) ⊆ n−(z). Then  satisfies B3. Next, suppose +(y) ⊆ n+(z) and +(x)
satisfies B3. Next, suppose +(y) ⊆ n+(z) and +(x)  +(y). Then +(y)
+(y). Then +(y)  +(x) and, by BT3, +(y)
+(x) and, by BT3, +(y)  n+(x). Then n+(x)
n+(x). Then n+(x)  n+(z). Then
n+(z). Then  satisfies B4. Next, suppose +(y) ⊆ n−(z) and +(x)
satisfies B4. Next, suppose +(y) ⊆ n−(z) and +(x)  + (y). Then, by BT3, n+(x)
+ (y). Then, by BT3, n+(x)  n+(z). Then
n+(z). Then  satisfies B5. Next, suppose + (z) ⊆ n+(y) and n+(x)
satisfies B5. Next, suppose + (z) ⊆ n+(y) and n+(x)  n−(y). Then, by BT5, n−(y) ⊆ n−(z). Then n+(x)
n−(y). Then, by BT5, n−(y) ⊆ n−(z). Then n+(x)  n−(z). Then
n−(z). Then  satisfies B6.
satisfies B6.
For ii) note that  4, specified in table 11, is a J-model but not a T3-model since condition BT3 is not satisfied. Note that + (a)
4, specified in table 11, is a J-model but not a T3-model since condition BT3 is not satisfied. Note that + (a)  + (b) but + (a) does not overlap n+ (b).
+ (b) but + (a) does not overlap n+ (b).
Though both T3-models and J-models, with the superstructural conditions defined above, will reveal the invalidity of any invalid syllogism with any finite number of antecedents (or premises), it is not clear that BT3 and BT5 are Aristotelian principles. Certainly BT4 is Aristotelian, given 25a27–28. And J-models may be simplified by replacing B3 with BT4, given the following theorem.
B4 (Darii LXL), B5 (Ferio LXL) and B6 (Baroco LLL) are Aristotelian given 30a37–b2 and 30a6–14 of the Prior Analytics.
5.2 Variants of the L-X-M system
Paul Thom in [1991, p. 137] points out that condition B2, used in the definitions of J-models and T3-models to guarantee that McCall’s axiom LIaa is valid, is unAristotelian. He says that it is unAristotelian to think that there are walkers that are essentially walkers and whites that are essentially white. Johnson’s [1993] and [1995] provide variants of McCall’s L-X-M that are sound and complete systems, where condition B2 is omitted. Both systems have 100% Aristotelicity. The systems deviate from McCall’s in that lines in deductions need not be axioms or lines that are ultimately derived from axioms by rules of inference. The systems are “natural deduction systems” rather than “axiomatic systems”. Proofs of completeness assume that the inferences under discussion satisfy what Smiley calls the “chain condition” in [Smiley, 1994, p. 27]. And the systems attempt to accommodate Aristotle’s proofs by ecthesis.19 In the remainder of this section we illustrate proofs by ecthesis and then discuss the chain condition in the next section.
In addition to sentences such as Abc and Labc discussed above we count m ∈ a (m is an a), m ∈n a (m is necessarily an a), m ∉n a (m is necessarily not an a), etc. The latter are singular sentences. In contrast to Thom’s view, to present proofs by ecthesis singular sentences are required.20 Consider this proof of Darapti XXX taken from Smith’s [1989, p. 9] with my additions in square brackets:
When they [terms] are universal, then when both P [that is, c] and R [that is, a] belong to every S [that is, b], it results of necessity that P will belong to some R. … It is … possible to carry out the demonstration through … the setting out [that is, by ecthesis]. For if both terms belong to every S, then if some one of the S’s is chosen (for instance N [that is, m], then both P and R will belong to this; consequently, P will belong to some R. (28a18–26)
Aristotle’s proof by ecthesis may be formalized as follows:
3. m ∈ b (By ecthesis from 1. Since all b are c there must be a b that may be referred to as m.)
4. m ∈ c (From 1 and 3. Since all b are c and m is a b it follows that m is a c.)
5. m ∈ a (From 2 and 3 by the reasoning for line 4.)
6. Iac (From 4 and 5 by “Existential Generalization” – if a particular object m is both an a and a c then something is both an a and a c.)
Aristotle proves that Baroco LLL is valid in the following passage, taken from Smith’s [1989, p. 13]:
… it is necessary for us to set out that part [m] to which each term [b and c] does not belong and produce the deduction about this [m]. For it will be necessary in application to each of these; and if it is necessary of what is set out, then it will be necessary of some part [a] of the former term (for what is set out is just a certain “that”. (30a9–15)
His proof by ecthesis may be formalized as follows:
1. LAcb (Premise. Whatever is c is necessarily b.)
2. LOab (Premise. There is something that is necessarily a but necessarily not b.)
4. m ∉n b (Lines 3 and 4 come from line 2 by ecthesis. This is a use of “Existential Instantiation”.)
5. m ∉n c (From 1 and 4. If whatever is c is necessarily b and m is necessarily not in c then m is necessarily not in c.)
6 The Chain Condition, Relevance Logic and The Ap System
The following remarks by Smiley from two of his papers show that Aristotle held views endorsed by contemporary “relevance logicians”.21
By building onto the propositional calculus Łukasiewicz in effect equates syllogistic implication with strict implication and thereby commits himself to embracing the novel moods corresponding to such theorems as ((Aab ∧ Oab) → Icd) or ((Aab ∧ Acd) → Aee). On the other hand Aristotle’s own omission of these syllogisms of strict implication, as they may be called can hardly be written off as an oversight. For they violate his dictum that a syllogism relating this to that proceeds from premises which relate this to that’ (41a6). This dictum is part of a principle which is absolutely fundamental to his syllogistic, namely the principle that the premises of a syllogism must form a chain of predications linking the terms of the conclusion. Thus his doctrine of the figures, which provides the framework for his detailed investigation of syllogistic, is founded on this principle (40b30 ff.) Not less important is that the chain principle is essential to the success of his attempt at a completeness proof for the syllogistic. By this I mean his attempt to show that every valid syllogistic inference, regardless of the number of premises, can be carried out by means of a succession of two-premise syllogisms. [Smiley, 1973, pp. 139–140]
Probably the easiest way to formulate this ‘chain condition’ is to use the notation AB to denote any of the forms a, e, i, o regardless whether the subject is A or B. Then the condition is that a valid argument must be of the form ‘AC, CD, DE, EF,…GH, HB; therefore AB’. The chain condition dramatically alters the character of the completeness problem (for a start, it excludes the possibility of anything following from an infinite number of premises) and it permits simple strategies for the proof that would otherwise be inconceivable. It is therefore not surprising that Aristotle’s proof should fail to fit the same picture as, for example, Corcoran’s own completeness proof for syllogistic logic without the chain condition [Corcoran, 1972].22 [Smiley, 1994, p. 27]
Aristotle’s case for the chain condition is redolent of relevance — the need for some overt connection of meaning between premises and conclusion as a prerequisite for deduction. [Smiley, 1994, p. 30]
Since McCall’s presentation of the L-X-M calculus imitates Łukasiewicz’s, it also embraces “novel moods” of the sort mentioned by Smiley. (LAab →(¬LAab →Icd)) is asserted in L-X-M even though neither c nor d occurs in the antecedent (and thus the consequent is irrelevant to the antecedents). This follows from the completeness result, mentioned above, for L-X-M. Note that for every model  either V
either V (LAab) = f or V
(LAab) = f or V (¬LAab = f. So
(¬LAab = f. So  (LAab → (¬LAab → Ide)). And (LEab → (LEcd → (LEef → Igg))) is asserted in L-X-M. For in every model
(LAab → (¬LAab → Ide)). And (LEab → (LEcd → (LEef → Igg))) is asserted in L-X-M. For in every model  , V
, V (Igg) = t. So
(Igg) = t. So  (LEab → (LEcd → (LEef → Igg))). So, by completeness,
(LEab → (LEcd → (LEef → Igg))). So, by completeness,  (LEab →(LEcd →(LEef →Igg))) even though g does not occur in any of the antecedents.
(LEab →(LEcd →(LEef →Igg))) even though g does not occur in any of the antecedents.
By using the chain condition in [1973], Smiley formulates an elegant decision procedure for the assertoric syllogistic. In [Johnson, 1994] a system is developed for Aristotle’s apodeictic syllogisms, call it the “AP system”, that uses the chain condition. A decision procedure is given for it that yields Smiley’s decision procedure as a corollary.23 Both decision procedures are given below.
Definition 6.1: (chain condition) Let Pri refer to “prefixes” of assertoric or apodeictic sentences: A, E, I, O, LA, LE, LI, LO, MA, ME, MI and MO. A chain is a set of sentences whose members can be arranged as a sequence 〈Pr1 [x1x2], Pr2[x2x3], …, Prn[xnx1] 〉, where Pri[xixj] is either Prixixj or Prixjxi and xi ≠ xj if i ≠ j.
So, for example, {LAab, MAcb, LIcd, Ead} and {Oba, LEbc, LEdc, LAda} are chains. But neither {LAaa} nor {LAab, Aba, MAac, Aca} is a chain.
Definition 6.2: (abbreviations for subsets of chains) X/LAxy refers to Axy or LAxy. X/LAx – y refers to Ø if x = y; otherwise, it refers to {X/LAz1z2, X/LAz2z3,…, X/LAzn-1 zn}, a subset of a chain, where x = z1, y = Zn and n > 1. LAx – y refers to Ø if x = y; otherwise it refers to X/LAx – z, LAzy, a subset of a chain. X/LExy refers to Exy or LExy. X/LIxy refers to Ixy or LIxy. And X/LOxy refers to Oxy or LOxy.
So, for example, LAab, LAbc, Acd has form X/LAa – d, but does not have form LAa – d. LAab, LAbc, Acd, LAd – e has form X/LAa – e and form LAa – e.
Definition 6.3: (contradictory of, cd) Let cd(Axy) = Oxy where ‘cd’ may be read as ‘the contradictory of’. Let cd(Ixy) = Exy, cd(LAxy) = MOxy, cd(LExy) = MIxy, cd(LIxy) = MExy, and cd(LOxy) = MAxy. And let cd(cd(x)) = x. So, for example, ad(Exy) = Ixy.
Theorem 6.4: (Johnson [1994], decision procedure for “AP-validity”) Suppose “validAP” (apodeictic syllogistic validity) is defined as in [1994]. Consider an inference in the “AP system” from premises P1, P2,…, Pn to conclusion C. This inference is validAP if and only if {P1, P2,…, Pn, cd(C)} is a chain that has one of the following eleven forms:
5. X/LAz-x, X/LAz-u, MAuv, X/LAv-y, LExy (or LEyx)
6. X/LAz-x, X/LAz-u, LAuy, MExy (or MEyx)
7. X/LAz-x, X/LAu-y, X/LIzu, X/LExy (or X/LEyx)
8. X/LAz-x, X/LAu-v, MAvw, X/LAw-y, X/LIzu (or X/LIuz), LExy (or LEyx)
9. X/LAz-x, X/LAu-y, MIzu, LExy (or LEyx)
11. X/LAz-x, X/LAu-v, LAvy, X/LIzu (or X/LIuz), MExy (or MEyx)
So, for example, {LAab, LAbc, Acd, cd(Aad)} has form 1. So ‘LAab, LAbc, Acd; so Aad’ is valid. {LAab, LAbc, Acd, cd(MAad)} has form 1. So ‘LAab, LAbc, Acd; so MAad’ is valid. {Aab, cd(Obc), Acd, Oad} has form 1. So ‘Aab, Acd, Oad; so Obc’ is valid. {MAac, LAcb, cd(MAab)} has form 2. So ‘MAac, LAcb; so MAab’ (Barbara LMM) is valid. {LAcb, Iac, cd(LIab)} has form 11. So ‘LAcb, Iac; so LIab’ (Darii LXL) is valid.
Notice that since ‘E’ occurs at most once in any of the forms, it follows that no valid syllogism, regardless of the number of premises, is such that ‘E’ occurs in two or more of its premises. A similar comment applies to occurrences of ‘M’.
The following result is a corollary of theorem 6.4.
Theorem 6.5: (Smiley [1973], decision procedure for “AS-validity”) Suppose “validAS” (assertoric syllogistic validity) is defined as in [1973]. Consider an inference in the assertoric syllogistic from premises P1, P2,…, Pn to conclusion C. This inference is validAS if and only if {P1, P2,…, Pn, cd(C)} is a chain that has one of the following three forms:
1. Ax-y, Oxy (restriction of form 1 of theorem 6.4)
2. Az-x, Az-y, Exy (restriction of form 4 of theorem 6.4)
3. XAz-x, Au-y, Izu, Exy (or Eyx) (restriction of form 7 of theorem 6.4)
So, for example, given form 2 of the corollary both ‘Aca, Acb; so Iab’ (Darapti) and ‘Aca, Eab; so Ocb’ (Celaront) are valid.
On table 13 a syllogism is marked as valid by referring by number to the form listed in theorem 6.4 in virtue of which it is valid. So, for example, the first occurrence of ‘1’ on the table indicates that Barbara XXX, XXM, XLX, XLM, LXX, LXM, LLX and LLM are valid in virtue of their relationship to {X/LAx — y, X/LOxy}. The 333 valid syllogisms marked on the table exactly match the 333 syllogisms that McCall accepts in his L-X-M system. See p. 46 of [McCall, 1963].
7 Contingent Syllogisms
A. N. Prior [1962, p. 188] gives a simple account of “the usual meaning of ‘contingent’” in the following passage:
In the De Interpretatione Aristotle remarks that the word ‘possible’ is ambiguous; we should sometimes say that ‘It is possible that p’ follows from ‘It is necessary that p’, but sometimes that it is inconsistent with it. In the former sense ‘possible’ means simply ‘not impossible’; in the latter sense, ‘neither impossible nor necessary’. It is for ‘possible’ in this second sense that the word ‘contingent’ is generally used. That is, ‘It is contingent that p’ means ‘Both p and not-p are possible’, KMpMNp [or (Mp ∧ M¬p)]. Contingency in this sense stands between necessity and impossibility, but in quite a different way from that in which the simply factual stands between the necessary and the possible. It is not that necessity implies contingency, and contingency impossibility; rather we have three mutually exclusive alternatives which divide the field between them — either a proposition is necessary, or it is neither-necessary-nor-impossible (i.e. contingent), or it is impossible.…
On p. 190 of [1962] Prior introduces the symbol ‘Q’ and reads ‘Qp’ as ‘It is contingent that p’. McCall adopts Prior’s use of ‘Q’ to refer to Aristotle’s contingency operator and Thom [1994, p. 91] refers to [McCall, 1963] to support his use of ‘Q’ in his discussions of contingency. In the discussion below, we shall also use ‘Q’.24
Thom makes the following remarks about contingency at the beginning of his article (p. 91):
Aristotle’s contingency syllogistic deals with the logic of derivations involving propositions that contain an expressed mode of contingency. The contingent is defined at I. 13, 32a 18–20, as that which is not necessary, but which being supposed does not result in anything impossible, i.e. as two-sided possibility.
Fitting Prior’s remarks, the two sides of contingency (Q) are necessity and impossibility. The one side of possibility (M) is impossibility.
McCall in [1963] diminishes and extends the L-X-M calculus, formulating the Q-L-X-M calculus. We give the basis for it.
Formation rules
Use the formation rules for L-X-M, amending FR2’ as follows.
| FR2’ | If p is a categorical expression then ¬p is a categorical expression and Lp and Qp are wffs. |
Assertion axioms
Use A0–A4 from system ŁA and A5–A14 from system L-X-M. So A2 is IAA. Add the following axioms.
| A15 (Barbara QQQ) |  (QAbc →(QAab →QAac)) (QAbc →(QAab →QAac)) |
| A16 (Darii QQQ) |  (QAbc →(QIab →QIac)) (QAbc →(QIab →QIac)) |
| A17 (QXQ-AAE, figure 1) |  (QAbc →(Aab →QEac)) (QAbc →(Aab →QEac)) |
| A18 (Darii QXQ) |  (QAbc →(Iab →QIac)) (QAbc →(Iab →QIac)) |
| A19 (Barbara XQM) |  (Abc →(QAab →MAac)) (Abc →(QAab →MAac)) |
| A20 (Celarent XQM) |  (Ebc →(QAab →MEac)) (Ebc →(QAab →MEac)) |
| A21 (Ferio XQM) |  (Ebc →(QIab →MOac)) (Ebc →(QIab →MOac)) |
| A22 (complementary conversion, QE-QA) |  (QEab →QAab) (QEab →QAab) |
| A23 (complementary conversion, QI-QO) |  (QIab →QOab) (QIab →QOab) |
| A24 (complementary conversion, QO-QI) |  (QOab →QIab) (QOab →QIab) |
| A25 (QI conversion) |  (QIab →QIba) (QIab →QIba) |
| A26 (QE-ME subordination) |  (QEab →MEab) (QEab →MEab) |
| A27 (QI-MI subordination) |  (QIab →MIab) (QIab →MIab) |
| A28 (QO-MO subordination) |  (QOab →MOab) (QOab →MOab) |
Assertion transformation rules
Use the assertion tranformation rules for L-X-M.
On p. 76 of [1963] McCall gives the following reason for changing A2 from LIaa to Iaa.
If we retain the axiom LIaa, we may, by means of the substitution CKQAacLIaaIac [((QAac ∧ LIaa) → Iac))] of Darii QLX (proved below), derive the implication CQAacIac [(QAac → Iac)], which is unAristotelian.
We shall present this reasoning systematically.
McCall devised his system Q-L-X-M so that it has this feature: (QEab → QEba) is not accepted. He wishes to reflect Aristotle’s view that universally negative contingent propositions are not convertible.25 McCall puts Aristotle’s argument for the non-convertibility of such propositions as follows:
… in 36b35-37a3, Aristotle gives what is in essence the following argument. We know that QAab implies QEab, and that QEba implies QAba [by complementary conversion]. Therefore if QEab implied QEba, QAab would imply QAba, which it does not. Hence QEab is not convertible.
But, unfortunately, McCall’s Q-L-X-M system is too strong. It forces us, for example, to accept (QAbc → (LAab → LAde)), which is clearly unAristotelian. It does not satisfy the chain condition mentioned above. After showing this, we shall lay out a system that is semantically consistent and maximizes Aristotelicity.
7.1 Overlooked acceptances in the Q-L-X-M system
McCall claims that Barbara QLX is not a thesis in his Q-L-X-M system. See table 13 on p. 92 of [1963]. But this result is a corollary of the following theorem.
1.  (Eca → (QAbc → MEba)) (by A20 and US)
(Eca → (QAbc → MEba)) (by A20 and US)
2.  (LAab → LIba) (by Ap-sub-a)
(LAab → LIba) (by Ap-sub-a)
3.  (MEba → MOab) (from 2 by RV and SE)
(MEba → MOab) (from 2 by RV and SE)
4.  (Eca → (QAbc → MOab)) (from 1 and 3 by CW)
(Eca → (QAbc → MOab)) (from 1 and 3 by CW)
5.  (QAbc → (LAab → Ica)) (from 4 by AI, RV and SE)
(QAbc → (LAab → Ica)) (from 4 by AI, RV and SE)
6.  (LAab → (Ice → LIcb)) (A7 and US)
(LAab → (Ice → LIcb)) (A7 and US)
7.  ((QAbc → (LAab → Ica)) → ((LAab → (Ica → LIcb)) → (QAbc → (LAab → LIcb)))) (by AO)
((QAbc → (LAab → Ica)) → ((LAab → (Ica → LIcb)) → (QAbc → (LAab → LIcb)))) (by AO)
8.  (QAbc → (LAab → LIcb)) (from 5, 6 and 7 by MP)
(QAbc → (LAab → LIcb)) (from 5, 6 and 7 by MP)
9.  (QAbc → QEbc) (by CC and US)
(QAbc → QEbc) (by CC and US)
10.  (QEbc → MEbc) (by A26 and US)
(QEbc → MEbc) (by A26 and US)
11.  (MEbc → MEcb) (by Ap-con and US)
(MEbc → MEcb) (by Ap-con and US)
12.  (QAbc → MEcb) (from 9, 10 and 11 by CW)
(QAbc → MEcb) (from 9, 10 and 11 by CW)
13.  (QAbc → ¬LIcb) (from 12 by SE)
(QAbc → ¬LIcb) (from 12 by SE)
14.  ((QAbc → (LAab → LIcb)) → ((QAbc → ¬LIcb) → (QAbc → (LAab → x)))) (by A0)
((QAbc → (LAab → LIcb)) → ((QAbc → ¬LIcb) → (QAbc → (LAab → x)))) (by A0)
The following theorem provides additional evidence that McCall’s Q-L-X-M system is too strong to be Aristotelian.
1.  (Eac → (QIba → MObc)) (by A21 and US)
(Eac → (QIba → MObc)) (by A21 and US)
2.  (QAab → QIba) (by A18, US, A2, MP)
(QAab → QIba) (by A18, US, A2, MP)
3.  (Eac → (QAab → MObc)) (from 1 and 2 by AS)
(Eac → (QAab → MObc)) (from 1 and 2 by AS)
4.  (LAbc → (QAab → Iac)) (from 3 by RV and SE)
(LAbc → (QAab → Iac)) (from 3 by RV and SE)
6.  (LAbc → (QAab → Ica)) (from 4 and 5 by CW)
(LAbc → (QAab → Ica)) (from 4 and 5 by CW)
7.  (QAab → (Ica → QIcb)) (by A18)
(QAab → (Ica → QIcb)) (by A18)
8.  ((LAbc → (QAab → Ica)) → ((QAab → (Ica → QIcb)) → (LAbc → (QAab → QIcb)))) (by AO)
((LAbc → (QAab → Ica)) → ((QAab → (Ica → QIcb)) → (LAbc → (QAab → QIcb)))) (by AO)
9.  (LAbc → (QAab → QIcb)) (from 6, 7 and 8 by MP)
(LAbc → (QAab → QIcb)) (from 6, 7 and 8 by MP)
10.  (QIcb → QIbc) (by A25 and US)
(QIcb → QIbc) (by A25 and US)
11.  (QIbc → QObc) (by A23 and US)
(QIbc → QObc) (by A23 and US)
12.  (QObc → MObc) (by A28 and US)
(QObc → MObc) (by A28 and US)
13.  (LAbc → (QAab → MObc)) (from 9, 10, 11 and 12 by MP)
(LAbc → (QAab → MObc)) (from 9, 10, 11 and 12 by MP)
14.  (LAbc → (QAab → ¬LAbc)) (from 13 by SE)
(LAbc → (QAab → ¬LAbc)) (from 13 by SE)
According to McCall’s table 13 on p. 92 of [McCall, 1963], sentences representing Barbara QLX, Barbara LQX, Barbara LQQ, Baroco QXM and Bocardo XQM are not accepted in the Q-L-X-M system, though they correspond to inferences that Aristotle considered to be valid. But it is an immediate consequence of theorems 7.1 and 7.2 that the first three sentences are accepted. That the last two are accepted may be seen as follows:
1.  (LAbc → (QAab → Aac)) (by theorem 7.2)
(LAbc → (QAab → Aac)) (by theorem 7.2)
2.  (Oac → (QAab → MObc)) (from 1 by RV and SE)
(Oac → (QAab → MObc)) (from 1 by RV and SE)
3.  (Obc → (QAba → MOac)) (Bocardo XQM, from 2 by US)
(Obc → (QAba → MOac)) (Bocardo XQM, from 2 by US)
4.  (QAbc → (LAab → Aac)) (by theorem 7.1)
(QAbc → (LAab → Aac)) (by theorem 7.1)
So McCall’s claim on p. 93 of [1963] that Q-L-X-M has 85% Aristotelicity needs to be modified. Instead of 24 “non-Aristotelian moods” out of 154 moods marked on his table 13, there are 29 out of 154. So the Aristotelicity of the Q-L-X-M system is about 81%.
When determining the Aristotelicity of a system, McCall only uses figures 1, 2 and 3 and none of the “subaltern moods” such as Barbari. Given theorems 7.1 and 7.2, the following wffs are accepted in Q-L-X-M, though they are not marked as accepted on McCall’s table 13: Bramantip QLQ, Camenes LQQ, Fesapo QLQ and Barbari LQQ.
In the following section we modify Q-L-X-M so that the resulting system, QLXM’, does not have the unAristotelian features that result from theorems 7.1 and 7.2. Given the data – that Aristotle regarded Barbara LQM as invalid and Bocardo QLM as valid, for example – it is a virtue of the modified system that it does not have 100% Aristotelicity. Note that if  (QObc → (LAba → MOac)) (Bocardo QLM) then
(QObc → (LAba → MOac)) (Bocardo QLM) then  (LAac → (QObc → MOba)) (Baroco LQM) by Reversal. In system QLXM’ both Barbara LQM and Bocardo QLM are invalid. In contrast, in system Q-L-X-M both are valid.
(LAac → (QObc → MOba)) (Baroco LQM) by Reversal. In system QLXM’ both Barbara LQM and Bocardo QLM are invalid. In contrast, in system Q-L-X-M both are valid.