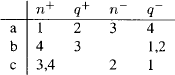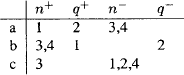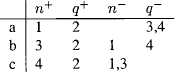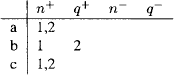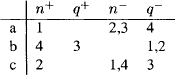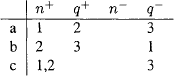8 Qlxm’
To ensure that theorems 7.2 and 7.1 may not be proven in system QLXM’ we exclude axioms A20 (Celarent XQM) and A21 (Ferio XQM). This decision is not difficult to make since, as McCall points out, Aristotle’s proofs of Celarent XQM and Ferio XQM are flawed. McCall shows that one who endorses such reasoning, thinking that “what is impossible cannot follow from what is merely false, but not impossible”, is committed to the absurd consequence that ‘Some B are A; all C are A; so some C are A’ is valid.
Only one other Q-L-X-M axiom is excluded to form QLXM′: delete axiom A28,  (QOab → MOab). This decision is a result of semantic considerations. For A28 to be validity preserving QOab and LAab must be semantically inconsistent. Since LAab is true iff + (a) ⊆ n+(b), we could make QOab and LAab contraries by fixing the semantics so that QOab is true iff + (a)
(QOab → MOab). This decision is a result of semantic considerations. For A28 to be validity preserving QOab and LAab must be semantically inconsistent. Since LAab is true iff + (a) ⊆ n+(b), we could make QOab and LAab contraries by fixing the semantics so that QOab is true iff + (a)  q(b). But then we are forced to say that Bocardo QLQ, for example, is valid even though Aristotle considered it to be invalid. (Suppose that V
q(b). But then we are forced to say that Bocardo QLQ, for example, is valid even though Aristotle considered it to be invalid. (Suppose that V (QOab) = t and V
(QOab) = t and V (LAac) = t. Then +(a)
(LAac) = t. Then +(a)  q(b) and +(a) ⊆ n+(c). Then n+(c)
q(b) and +(a) ⊆ n+(c). Then n+(c)  q(b). Then +(c)
q(b). Then +(c)  q(b). Then V
q(b). Then V (QOcb) = t.) Note, also, that if QOab is true iff +(a)
(QOcb) = t.) Note, also, that if QOab is true iff +(a)  q(b) then we would want to ensure that QIab is true iff +(a)
q(b) then we would want to ensure that QIab is true iff +(a)  q(b) to guarantee the soundness of the complementary conversion principles that Aristotle clearly supported. But then we would be forced to say that Disamis QLQ is valid even though Aristotle considered it to be invalid. (Suppose that V
q(b) to guarantee the soundness of the complementary conversion principles that Aristotle clearly supported. But then we would be forced to say that Disamis QLQ is valid even though Aristotle considered it to be invalid. (Suppose that V (QIbc) = t and V
(QIbc) = t and V (LAba) = t. Then +(b)
(LAba) = t. Then +(b)  q(c) and +(b) ⊆ n+(a). Then n+(a)
q(c) and +(b) ⊆ n+(a). Then n+(a)  q(c). Then +(a)
q(c). Then +(a)  q(c). Then V
q(c). Then V (QIac) = t.) Similar remarks may be made about Disamis QXQ, Datisi LQQ and Datisi XQQ.
(QIac) = t.) Similar remarks may be made about Disamis QXQ, Datisi LQQ and Datisi XQQ.
Rather than fixing the conditions for the truth of QOab as indicated above we may let QOab be true iff either QIab or QIba is true.26 To make A28 truth preserving we must ensure that if LAab is true then both QIab and QIba are false. Such a position does not fit the sorts of examples Aristotle uses. Suppose, for example, that all things that are sleeping are necessarily men. It does not follow that it is not true that some men are contingently sleeping.
We avoid the above difficulties by deleting axiom A28 when defining QLXM’.
In this system, as in Q-L-X-M, there are no rejection axioms and no rejection rules.
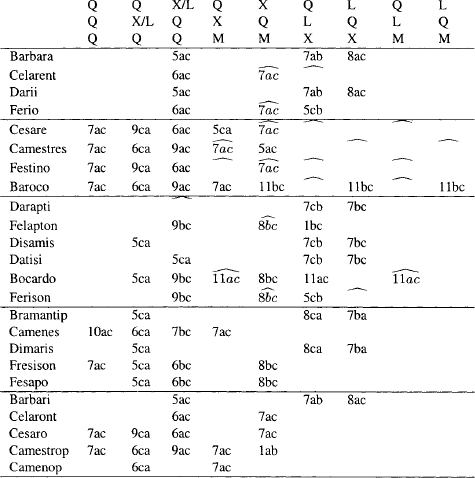
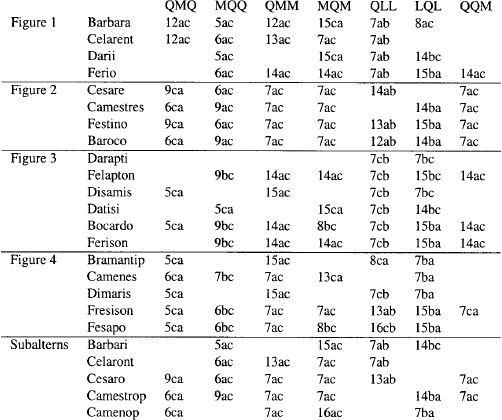
Before giving a semantics for QLXM’ we shall establish some immediate inferences that are conversions, subalternations or subordinations. With them we shall show the acceptance of various two-premised syllogisms indicated on table 15 by leaving a cell unmarked. After the semantics is given we shall show that sentences corresponding to the other cells, those in which numerals occur, are invalid. An occurrence of the “hat sign” in a cell in the table means the entry conflicts with Aristotle’s judgments about validity as recorded on McCall’s authoritative table 12 of [McCall, 1963].27
McCall follows Ross’s use of “complementary conversion” to refer to A22 to A24. On p. 298 of [Ross, 1949] Ross, in his discussion of 35a29–b1, identifies the following entailments, endorsed by Aristotle, as “complementary conversions”:
‘For all B, being A is contingent’ [QAba] entails ‘For all B, not being A is contingent’ [QEba] and ‘For some B, not being A is contingent’ [QOba]. ‘For all B, not being A is contingent’ [QEba] entails ‘For all B, being A is contingent’ [QAba] and ‘For some B, being A is contingent’ [QIba]. ‘For some B, being A is contingent’ [QIba] entails ‘For some B, not being A is contingent’ [QOba]. ‘For some B, not being A is contingent’ [QOba] entails ‘For some B, being A is contingent’ [QIba].
Given the following theorem and US, Ross’s six complementary conversions are asserted in QLXM’.
Theorem 8.3: (Complementary conversion, CC) i)  (QAab → QEab); ii)
(QAab → QEab); ii)  (QAab → QOab); iii)
(QAab → QOab); iii)  (QEab → QAab); iv)
(QEab → QAab); iv)  (QEab → QIab); v)
(QEab → QIab); v)  (QIab → QOab); and vi)
(QIab → QOab); and vi)  (QOab → QIab).
(QOab → QIab).
Proof: For i) use A17, US, AI, A1 and MP. For ii) use Q-sub-a, A23 and CW. iii) is A22. For iv) use iii), Q-sub-a and CW. v) is A23. vi) is A24.
Theorem 8.4: (Complementary conversions per accidens, CC(pa)) i)  (QAab → QIba); ii)
(QAab → QIba); ii)  (QAab → QOba); iii)
(QAab → QOba); iii)  (QEab → QIba); and iv)
(QEab → QIba); and iv)  (QEab → QOba).
(QEab → QOba).
Proof: For i) use Q-sub-a, Q-con, US and CW. For ii) use i), A23, US and CW. For iii) use i), A22 and AS. For iv) use iii), A23, US and CW.
Uses of AS or CW in proofs of the following theorems involve only those immediate inferences that have been proven above. So, for example, in the proof that Celarent QQQ is asserted AS is used with Q-sub-a and US ( (QEbc → QAbc)) and CW is used with Q-sub-a and US (
(QEbc → QAbc)) and CW is used with Q-sub-a and US ( (QAac → QEac)).
(QAac → QEac)).
Theorem 8.6: (asserted QQQs) The non-numbered QQQ cells on table 15 correspond to asserted sentences.
1.  (QAbc →(QAab →QAac)) (Barbara QQQ, by A17)
(QAbc →(QAab →QAac)) (Barbara QQQ, by A17)
2.  (QEbc →(QAab →QEac)) (Celarent QQQ, from 1 by AS, US, CW)
(QEbc →(QAab →QEac)) (Celarent QQQ, from 1 by AS, US, CW)
3.  (QAbc →(QIab →QIac)) (Darii QQQ, by A16)
(QAbc →(QIab →QIac)) (Darii QQQ, by A16)
4.  (QEbc →(QIab →QOac)) (Ferio QQQ, from 3 by AS, US, CW)
(QEbc →(QIab →QOac)) (Ferio QQQ, from 3 by AS, US, CW)
5.  (QAbc →(QAba →QIac)) (Darapti QQQ, from 3 by AS, US)
(QAbc →(QAba →QIac)) (Darapti QQQ, from 3 by AS, US)
6.  (QEbc →(QAba →QOac)) (Felapton QQQ, from 5 by AS, US, CW)
(QEbc →(QAba →QOac)) (Felapton QQQ, from 5 by AS, US, CW)
7.  (QAbc →(QIba →QIac)) (Datisi QQQ, from 3 by AS, US)
(QAbc →(QIba →QIac)) (Datisi QQQ, from 3 by AS, US)
8.  (QEbc →(QIba →QOac)) (Ferison QQQ, from 7 by AS, US, CW)
(QEbc →(QIba →QOac)) (Ferison QQQ, from 7 by AS, US, CW)
9.  (QIbc →(QAba →QIac)) (Disamis QQQ, from 7 by AI, CW, US)
(QIbc →(QAba →QIac)) (Disamis QQQ, from 7 by AI, CW, US)
10.  (QObc →(QAba →QOac)) (Bocardo QQQ, from 9 by AS, US, CW)
(QObc →(QAba →QOac)) (Bocardo QQQ, from 9 by AS, US, CW)
11.  (QIcb →(QAba →QIac)) (Dimaris QQQ, from 9 by AS, US)
(QIcb →(QAba →QIac)) (Dimaris QQQ, from 9 by AS, US)
12.  (QAcb →(QAba →QIac)) (Bramantip QQQ, from 11 by AS, US)
(QAcb →(QAba →QIac)) (Bramantip QQQ, from 11 by AS, US)
13.  (QEcb →(QAba →QOac)) (Fesapo QQQ, from 12 by AS, US, CW)
(QEcb →(QAba →QOac)) (Fesapo QQQ, from 12 by AS, US, CW)
14.  (QAbc →(QAab →QAac)) (Barbari QQQ, from 1 by CW, US)
(QAbc →(QAab →QAac)) (Barbari QQQ, from 1 by CW, US)
15.  (QEbc →(QAab →QEac)) (Celaront QQQ, from 2 by CW, US)
(QEbc →(QAab →QEac)) (Celaront QQQ, from 2 by CW, US)
16.  (QAcb →(QEba →QOac)) (Camenop QQQ, from 12 by AS, US, CW)
(QAcb →(QEba →QOac)) (Camenop QQQ, from 12 by AS, US, CW)
Theorem 8.7: (asserted QXQs and XQQs) The non-numbered QXQ and XQQ cells on table 15 correspond to asserted sentences.
1.  (QAbc →(Aab →QAac)) (Barbara QXQ, by A17, US, CW)
(QAbc →(Aab →QAac)) (Barbara QXQ, by A17, US, CW)
2.  (QEbc →(Aab →QEac)) (Celarent QXQ, from 1 by AS, US, CW)
(QEbc →(Aab →QEac)) (Celarent QXQ, from 1 by AS, US, CW)
3.  (QAbc →(Iab →QIac)) (Darii QXQ, by A18)
(QAbc →(Iab →QIac)) (Darii QXQ, by A18)
4.  (QEbc →(Iab →QOac)) (Ferio QXQ, from 3 by AS, US, CW)
(QEbc →(Iab →QOac)) (Ferio QXQ, from 3 by AS, US, CW)
5.  (QAbc →(Iba →QIac)) (Datisi QXQ, from 3 by AS, US)
(QAbc →(Iba →QIac)) (Datisi QXQ, from 3 by AS, US)
6.  (QEbc →(Iba →QOac)) (Ferison QXQ, from 5 by AS, US, CW)
(QEbc →(Iba →QOac)) (Ferison QXQ, from 5 by AS, US, CW)
7.  (QAbc →(Aba →QIac)) (Darapti QXQ, from 5 by AS, US)
(QAbc →(Aba →QIac)) (Darapti QXQ, from 5 by AS, US)
8.  (QEbc →(Aba →QOac)) (Felapton QXQ, from 7 by AS, US, CW)
(QEbc →(Aba →QOac)) (Felapton QXQ, from 7 by AS, US, CW)
9.  (QAbc →(Aab →QIac)) (Barbari QXQ, from 1 by US, CW)
(QAbc →(Aab →QIac)) (Barbari QXQ, from 1 by US, CW)
10.  (QEbc →(Aab →QOac)) (Celaront QXQ, from 2 by US, CW)
(QEbc →(Aab →QOac)) (Celaront QXQ, from 2 by US, CW)
11.  (Ibc →(QAba →QIac)) (Disamis XQQ, from 5 by AI, CW, US)
(Ibc →(QAba →QIac)) (Disamis XQQ, from 5 by AI, CW, US)
12.  (Abc →(QAba →QIac)) (Darapti XQQ, from 11 by AS)
(Abc →(QAba →QIac)) (Darapti XQQ, from 11 by AS)
13.  (Icb →(QAba →QIac)) (Dimaris XQQ, from 11 by AS)
(Icb →(QAba →QIac)) (Dimaris XQQ, from 11 by AS)
Theorem 8.8: (asserted QLQs and LQQs) The non-numbered QLQ and LQQ cells on table 15 correspond to asserted sentences.
Proof: Use theorem 8.7 and Sub-o.
So, for example,  (QAbc →(LAab →QAac)) since
(QAbc →(LAab →QAac)) since  (QAbc →(Aab →QAac)) by theorem 8.7 and since
(QAbc →(Aab →QAac)) by theorem 8.7 and since  (LAab →Aab) by Sub-o.
(LAab →Aab) by Sub-o.
Theorem 8.9: (asserted QXMs and XQMs) The non-numbered QXM and XQM cells on table 15 correspond to asserted sentences.
Proof: For non-numbered QXM and XQM cells referred to by names that do not end with ‘o’ use theorem 8.7 wherever possible with Q-sub-o and CW. So Barbara QXM is asserted since Barbara QXQ is assserted. And, by this reasoning, Celarent QXM, Darii QXM, Darapti QXM, Datisi QXM, Barbari QXM, Darapti XQM, Disamis XQM, Bramantip XQM, Camenes XQM, Dimaris XQM and Barbari XQM. For the remaining non-numbered cells use asserted MXM syllogisms from table 13 wherever possibile with Q-sub-o and AS. So, Ferio QXM is accepted since Ferio MXM is accepted. And, by this reasoning, Festino QXM, Felapton QXM, Disamis QXM, Ferison QXM, Bramantip QXM, Dimaris QXM, Fresison QXM, Fesapo QXM, Celaront QXM, Cesaro QXM, Darii XQM, Datisi XQM and Barbari XQM. The only remaining non-numbered QXM and XQM cells correspond to the axiom Barbara XQM (A21) and Camenop XQM, which is deduced from Camenes XQM by CW given Ap-sub-a.
Theorem 8.10: (asserted QLXs and LQXs) The non-numbered QLX and LQX cells on table 15 correspond to asserted sentences.
In the following proof the asterisks mark inconsistencies in the data as reported on McCall’s table 12 on pp. 84–85 of [1963].
Proof: Use theorem 8.9 with RV and SE. So i) Celarent QLX is asserted since Festino QXM is asserted; ii) Celaront QLX (is asserted) since Cesaro QXM (is asserted); iii)* Cesare QLX since Ferio QXM; iv) Camestres QLX since Darii QXM; v)* Festino QLX since Celarent QXM; vi)* Baroco QLX since Barbara QXM; vii) Cesaro QLX since Celaront QXM; viii) Camestrop QLX since Barbari QXM; ix) Camenes QLX since Dimaris XQM; x) Fresison QLX since Camenes XQM; xi) Fesapo QLX since Camenop XQM; xii) Camenop QLX since Bramantip XQM; xiii) Celarent LQX since Disamis XQM; xiv) Ferio LQX since Datisi XQM; xv) Celaront LQX since Barbari XQM; xvi) Cesare LQX since Datisi QXM; xvii)* Camestres LQX since Ferison QXM; xviii) Festino LQX since Disamis QXM; xix) Cesaro LQX since Darapti QXM; xx) Camestrop LQX since Felapton QXM; xxi) Felapton LQX since Barbari XQM; xxii) Bocardo LQX since Barbara XQM; xxiii)* Ferison LQX since Darii XQM; xxiv) Camenes LQX since Fresison QXM; xxv) Fresison LQX since Dimaris QXM; xxvi) Fesapo LQX since Bramantip QXM; and xxvii) Camenop LQX since Fesapo QXM.
Theorem 8.11: The non-numbered QLM and LQM cells on table 15 correspond to asserted sentences.
Proof: For the QLMs use: i) results for the accepted QXM syllogisms stated in theorem 8.9, Sub-o and AS; or ii) results for the accepted QLX syllogisms stated in theorem 8.10, Sub-o and CW. So, for example,  (QAbc → (LAab → MAac)) (Barbara QLM is asserted) since
(QAbc → (LAab → MAac)) (Barbara QLM is asserted) since  (QAbc → (Aab → MAac)) and
(QAbc → (Aab → MAac)) and  (LAab → Aab) given AS.
(LAab → Aab) given AS.  (QEcb → (LAab → MEac)) (Cesare QLM is asserted) since
(QEcb → (LAab → MEac)) (Cesare QLM is asserted) since  (QEcb → (LAab → Eac)) and
(QEcb → (LAab → Eac)) and  (Eac → MEac).
(Eac → MEac).
For the LQMs use results for the XQMs in theorem 8.9 or the LQXs in theorem 8.10 together with Sub-o, AS or CW. So, for example,  (LAbc → (QIab → MIac)) (Darii LQM is asserted) since
(LAbc → (QIab → MIac)) (Darii LQM is asserted) since  (LAbc → (QIab → Iac)) and
(LAbc → (QIab → Iac)) and  (Iac → MIac).
(Iac → MIac).  (LEbc → (QIab → MOac)) (Ferio LQM is asserted) since
(LEbc → (QIab → MOac)) (Ferio LQM is asserted) since  (LEbc → (QIab → Oac)) and
(LEbc → (QIab → Oac)) and  (Oac → MOac)).
(Oac → MOac)).
Theorem 8.12: The non-numbered QQMs on table 15 correspond to asserted sentences.
Proof: Obtain the assertion of Barbara QQM from the assertion of Barbara QQQ by using CW with Q-sub-o. Use similar reasoning for Celarent, Darii, Barbari, Darapti, Disamis, Datisi, Bramantip and Dimaris. We generate the remaining four QQMs as follows.
1.  (QEbc → (QAab → QEac)) (Celarent QQQ)
(QEbc → (QAab → QEac)) (Celarent QQQ)
3.  (MEac → MOac) (by Ap-sub-a)
(MEac → MOac) (by Ap-sub-a)
4.  (QEac → MOac) (from 2 and 3 by CW)
(QEac → MOac) (from 2 and 3 by CW)
5.  (QEbc → (QAab → MOac)) (Celaront QQM, from 1 and 4 by CW)
(QEbc → (QAab → MOac)) (Celaront QQM, from 1 and 4 by CW)
6.  (QAab → (QEbc → QEac)) (from 1 by AI)
(QAab → (QEbc → QEac)) (from 1 by AI)
8.  (QEac → MEca) (from 2 and 7 by CW)
(QEac → MEca) (from 2 and 7 by CW)
9.  (QAab → (QEbc → MEca)) (from 6 and 8 by CW)
(QAab → (QEbc → MEca)) (from 6 and 8 by CW)
10.  (QAcb → (QEba → MEac)) (Camenes QQM, from 9 by US)
(QAcb → (QEba → MEac)) (Camenes QQM, from 9 by US)
11.  (MEac → MOac) (Ap-sub-a and US)
(MEac → MOac) (Ap-sub-a and US)
12.  (QAcb → (QEba → MOac)) (Camenop QQM, from 10 and 11 by CW)
(QAcb → (QEba → MOac)) (Camenop QQM, from 10 and 11 by CW)
13.  (QEcb → (QAba → MOac)) (Fesapo QQM, from 12 by CC and AS)
(QEcb → (QAba → MOac)) (Fesapo QQM, from 12 by CC and AS)
8.1 Semantics for QLXM’
The semantics for QLXM’ is given by referring to Q-models.
Definition 8.13: (Q-model)  is a Q-model iff
is a Q-model iff  = 〈W, n+,q+,n−,q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”:
= 〈W, n+,q+,n−,q−〉, where W is a non-empty set and n+, q+, n−, and q− are functions that map terms into subsets of W and satisfy the following “base conditions”:
| BQ1 | If f and g are any of the functions n+,q+,q− or n− and f ≠ g, then, for every term x, f(x) ∩g(x) = Ø and for every x, n+(x) ∪q+(x) ∪ q− (x) ∪ n−(x) = W |
| BQ2 | (For every x and y) if + (x) ⊆ n−(y) then +(y) ⊆ n−(z) |
| BQ3 | If + (y) ⊆ n+(z) and +(x)  +(y) then n+(x) +(y) then n+(x)  n+(z) n+(z) |
| BQ4 | If + (y) ⊆ n−(z) and +(x)  + (y) then n+(x) + (y) then n+(x)  n− (z) n− (z) |
| BQ5 | If + (z) ⊆ n+(y) and n+(x)  n− (y) then n+(x) n− (y) then n+(x)  n− (z) n− (z) |
| BQ6 | If + (y) ⊆ q(z) and +(x) ⊆ q(y) then +(x) ⊆ q(z) |
| BQ7 | If + (y) ⊆ q(z) and + (x)  q(y) or q(x) q(y) or q(x)  +(y) then +(z) +(y) then +(z)  q(z) or q(z) & compfin; +(x) q(z) or q(z) & compfin; +(x) |
| BQ8 | If + (y) ⊆ +(z) and +(x) ⊆ q(y) then n+(x) does not overlap n− (z) |
Definition 8.14: (valuation relative to a Q-model) V is a valuation relative to a Q-model M
is a valuation relative to a Q-model M iff it is is a valuation that satisfies the following “superstructural conditions”:
iff it is is a valuation that satisfies the following “superstructural conditions”:
| S1 | (For every x and y) V (Axy) = t iff + (x) ⊆ + (y) (Axy) = t iff + (x) ⊆ + (y) |
| S2 | V (Ixy) = t iff + (x) (Ixy) = t iff + (x)  +(y). +(y). |
| S3 | V (LAxy) = t iff + (x) ⊆ n+(y) (LAxy) = t iff + (x) ⊆ n+(y) |
| S4 | V (LIxy) = t iff n+(x) (LIxy) = t iff n+(x)  n+(y) n+(y) |
| S5 | V (L¬Axy) = t iff n+(x) (L¬Axy) = t iff n+(x)  n−(y) n−(y) |
| S6 | V (L¬Ixy) = t iff + (x) ⊆ n−(y) (L¬Ixy) = t iff + (x) ⊆ n−(y) |
| S7 | V (QAxy) = t iff + (x) ⊆ q(y) (QAxy) = t iff + (x) ⊆ q(y) |
| S8 | V (QIxy) = t iff + (x) (QIxy) = t iff + (x)  q(y) or q(x) q(y) or q(x)  +(y) +(y) |
| S9 | V (Q¬Axy) = t iff + (x) (Q¬Axy) = t iff + (x)  q(y) or q(x) q(y) or q(x)  + (y) + (y) |
| S10 | V (Q¬Ixy) = t iff + (x) ⊆ q(y) (Q¬Ixy) = t iff + (x) ⊆ q(y) |
Definition 8.15: (Q-valid)  Q α (α is Q-valid) iff, for every Q-model
Q α (α is Q-valid) iff, for every Q-model  , VM (α) = t. α is Q-invalid (
, VM (α) = t. α is Q-invalid ( Q α) iff α is not Q-valid.
Q α) iff α is not Q-valid.
Proof: We need to show that i) if  α is an axiom of QLXM’ then
α is an axiom of QLXM’ then  Q α and ii) each assertion transformation rule of QLXM’ preserves Q-validity. Some examples of the reasoning needed are given. For A1,
Q α and ii) each assertion transformation rule of QLXM’ preserves Q-validity. Some examples of the reasoning needed are given. For A1,  Q Aaa since, for every Q-model
Q Aaa since, for every Q-model  , V
, V (Aaa) = t since +(a) ⊆ +(a). For A2,
(Aaa) = t since +(a) ⊆ +(a). For A2,  Q Iaa since, for every Q-model
Q Iaa since, for every Q-model  , V
, V ,(Iaa) = t since +(a)
,(Iaa) = t since +(a)  +(a). For A5, suppose there is a Q-model
+(a). For A5, suppose there is a Q-model  such that V
such that V (LAbc) = t, V
(LAbc) = t, V (Aab) = t and V
(Aab) = t and V (LAac) = f. Then +(b) ⊆ n+(c), +(a) ⊆ +(b) and +(a)
(LAac) = f. Then +(b) ⊆ n+(c), +(a) ⊆ +(b) and +(a)  n+(c), which is impossible. So
n+(c), which is impossible. So  Q (LAbc → (Aab → LAac)). For A15, suppose there is a Q-model
Q (LAbc → (Aab → LAac)). For A15, suppose there is a Q-model  such that V
such that V (QAbc) = t, V
(QAbc) = t, V (QAab) = t and V
(QAab) = t and V (QAac) = f. Then +(b) ⊆ q(c), +(a) ⊆ q(b) and +(a)
(QAac) = f. Then +(b) ⊆ q(c), +(a) ⊆ q(b) and +(a)  q(c), which is impossible given BQ6. So
q(c), which is impossible given BQ6. So  Q (QAbc → (QAab → QAac)). For AR1 suppose
Q (QAbc → (QAab → QAac)). For AR1 suppose  Q (…x…x…) but
Q (…x…x…) but  Q (…y…y…), where (…y…y…) is the result of replacing every occurrence of term x in (…x…x…) with term y. Then, for some Q-model
Q (…y…y…), where (…y…y…) is the result of replacing every occurrence of term x in (…x…x…) with term y. Then, for some Q-model  , V
, V (…y…y…) = f, where V
(…y…y…) = f, where V (y) is set S. Let V
(y) is set S. Let V (x) = S. Then V
(x) = S. Then V (…x…x…) = f. So it is impossible for AR1 not to preserve validity. For AR2 suppose a)
(…x…x…) = f. So it is impossible for AR1 not to preserve validity. For AR2 suppose a)  Q (p → q), b)
Q (p → q), b)  Q p and c)
Q p and c)  Q q. Then, for some Q-model
Q q. Then, for some Q-model  , V
, V (q) = f, given c). Then, by a), V
(q) = f, given c). Then, by a), V (p) = f, which conflicts with b). So AR2 preserves validity. Reasoning for the other axioms and rules is straightforward and is omitted.
(p) = f, which conflicts with b). So AR2 preserves validity. Reasoning for the other axioms and rules is straightforward and is omitted.
Given the soundness of QLXM’ every asserted sentence in Łukasiewicz’s ŁA is Q-valid since ŁA is a fragment of QLXMt. All of the L-X-M syllogisms marked as asserted on table 5 are Q-valid since all of them are asserted in QLXM’. And, given the following theorem, all of the syllogisms marked as invalid on table 5 are Q-invalid.
Proof: By earlier arguments the four models satisfy conditions BQ1 to BQ5. Consider  1. Suppose + (y) ⊆ q(z). Then z = c. So BQ6 is trivially satisfied. For all x, + (x)
1. Suppose + (y) ⊆ q(z). Then z = c. So BQ6 is trivially satisfied. For all x, + (x)  q(c). So BQ7 is satisfied. For all z, n−(z) = Ø. So BQ8 is satisfied. Consider
q(c). So BQ7 is satisfied. For all z, n−(z) = Ø. So BQ8 is satisfied. Consider  2. Suppose + (y) ⊆ q(z). Then y = a or y = b, and z = c. So BQ6 is trivially satisfied. For all x, + (x)
2. Suppose + (y) ⊆ q(z). Then y = a or y = b, and z = c. So BQ6 is trivially satisfied. For all x, + (x)  q(c). So BQ7 is satisfied. For all z, if + (c) ⊆+ (z) then z = c. Since n−(c) = Ø, BQ8 is satisfied. Consider
q(c). So BQ7 is satisfied. For all z, if + (c) ⊆+ (z) then z = c. Since n−(c) = Ø, BQ8 is satisfied. Consider  3. Suppose +(y) ⊆ q(z). Then y = b or y = c, and z = a. So BQ6 is trivially satisfied. For all x, + (a)
3. Suppose +(y) ⊆ q(z). Then y = b or y = c, and z = a. So BQ6 is trivially satisfied. For all x, + (a)  q (x). So BQ7 is satisfied. For all z, if + (a) ⊆ + (z) then z = a. Since n−(a) = Ø, BQ8 is satisfied. Consider
q (x). So BQ7 is satisfied. For all z, if + (a) ⊆ + (z) then z = a. Since n−(a) = Ø, BQ8 is satisfied. Consider  4. For all y and z, if + (y)
4. For all y and z, if + (y)  q(z). So BQ6, BQ7 and BQ8 are trivially satisfied.
q(z). So BQ6, BQ7 and BQ8 are trivially satisfied.
Table 16 expresses a model. BQ1 and BQ2, here and below, require no comment. For every y and z, if +(y) ⊆ n+(z) then z = c. For every x, n+(x)  n+(c). So BQ3 is satisfied. For every y and z, +(y)
n+(c). So BQ3 is satisfied. For every y and z, +(y)  n−(z). So BQ4 is trivially satisfied. If + (y) ⊆ n+(z) then z = c. For every x, y and z, if z ⊆ n+(y) then n+(x) does not overlap n−(y). So BQ5 is satisfied. For every x and y, if x ⊆ q(y) then x = a and y = b. So BQ6 is trivially satisfied. For all x, x
n−(z). So BQ4 is trivially satisfied. If + (y) ⊆ n+(z) then z = c. For every x, y and z, if z ⊆ n+(y) then n+(x) does not overlap n−(y). So BQ5 is satisfied. For every x and y, if x ⊆ q(y) then x = a and y = b. So BQ6 is trivially satisfied. For all x, x  q(b). So BQ7 is satisfied. For all z, +(a) does not overlap n−(z). So BQ8 is satisfied.
q(b). So BQ7 is satisfied. For all z, +(a) does not overlap n−(z). So BQ8 is satisfied.
Given Q-model  5,
5,  Q (LAbc → (QAab → LAac)). For, V
Q (LAbc → (QAab → LAac)). For, V 5(LAbc) = t since + (b) ⊆ n+(c). V
5(LAbc) = t since + (b) ⊆ n+(c). V 5(QAab) = t since +(a) ⊆ q(b). And V
5(QAab) = t since +(a) ⊆ q(b). And V 5 (QAac) = f since + (a)
5 (QAac) = f since + (a)  q(c). The occurrence of ‘4ac’ in the Barbara/LQQ cell indicates Q-model
q(c). The occurrence of ‘4ac’ in the Barbara/LQQ cell indicates Q-model  5 is a countermodel for Barbara LQQ, where ‘a’ is the minor term and ‘c’ is the major term. This method of listing minor and major terms will be followed below.
5 is a countermodel for Barbara LQQ, where ‘a’ is the minor term and ‘c’ is the major term. This method of listing minor and major terms will be followed below.
Table 17 expresses a model. For every y and z, if + (y) ⊆ n+(z) then y = z = c. For every x and y, if +(x)  +(y) then x = c. Since n+(c)
+(y) then x = c. Since n+(c)  n+(c), BQ3 is satisfied. For every y, if +(y) ⊆ n−(a) then y = b or y = c. For every x, if x
n+(c), BQ3 is satisfied. For every y, if +(y) ⊆ n−(a) then y = b or y = c. For every x, if x  +(b) or x
+(b) or x  +(c) then n+(x)
+(c) then n+(x)  n−(a). For every y, if + (y) ⊆ n−(b) then y = b. For every x, if x
n−(a). For every y, if + (y) ⊆ n−(b) then y = b. For every x, if x  +(b) then n+(x)
+(b) then n+(x)  n−(b). For every y, if +(y) ⊆ n− (c) then y = a or y = b. For every x, if x
n−(b). For every y, if +(y) ⊆ n− (c) then y = a or y = b. For every x, if x  +(a) or x
+(a) or x  +(b) then n+(x)
+(b) then n+(x)  n−(c). So B4 is satisfied. For every y and z, if + (z) ⊆ n+(y) then n−(y) ⊆ n−(z) (that is, Thomason’s BT5 is satisfied).28 So, BQ5 is satisfied. For every x and y, if +(x) ⊆ q(y) then x = a and q = b. So BQ6 is trivially satisfied. For all w, if + (w)
n−(c). So B4 is satisfied. For every y and z, if + (z) ⊆ n+(y) then n−(y) ⊆ n−(z) (that is, Thomason’s BT5 is satisfied).28 So, BQ5 is satisfied. For every x and y, if +(x) ⊆ q(y) then x = a and q = b. So BQ6 is trivially satisfied. For all w, if + (w)  q(a) or q(w)
q(a) or q(w)  +(a) then w = a or w = b. Since + (a)
+(a) then w = a or w = b. Since + (a)  q(b) and + (b)
q(b) and + (b)  q(b), BQ7 is satisfied. For every z, if + (b) ⊆ z then z = b. Since + (a) does not overlap n− (b), BQ8 is satisfied.
q(b), BQ7 is satisfied. For every z, if + (b) ⊆ z then z = b. Since + (a) does not overlap n− (b), BQ8 is satisfied.
Given Q-model  6, not
6, not  Q (LEac → (QAab → QObc)). For, VM6(LEac) = t since+(a) ⊆ n−(c). VM6(QAab) = t since +(a) ⊆ q(b). And VM6(QObc) = f since + (b) does not overlap q(c) and q(b) does not overlap +(c). The occurrence of ‘6bc’ in the Felapton/LQQ cell indicates that Q-model
Q (LEac → (QAab → QObc)). For, VM6(LEac) = t since+(a) ⊆ n−(c). VM6(QAab) = t since +(a) ⊆ q(b). And VM6(QObc) = f since + (b) does not overlap q(c) and q(b) does not overlap +(c). The occurrence of ‘6bc’ in the Felapton/LQQ cell indicates that Q-model  6 is a countermodel for Felapton LQQ, where ‘b’ is the minor term and ‘c’ is the major term.
6 is a countermodel for Felapton LQQ, where ‘b’ is the minor term and ‘c’ is the major term.
Table 18 expresses a Q-model. Since Thomason’s BT3 (if +(x)  +(y) then +(x)
+(y) then +(x)  n+(y)) is satisfied, both BQ3 and BQ4 are satisfied. Since BT5 is satisfied BQ5 is satisfied. If +(x) ⊆ q(y) then y = b and either x = a or x = c. Then BQ6 is trivially satisfied. If+ (z)
n+(y)) is satisfied, both BQ3 and BQ4 are satisfied. Since BT5 is satisfied BQ5 is satisfied. If +(x) ⊆ q(y) then y = b and either x = a or x = c. Then BQ6 is trivially satisfied. If+ (z)  q(a) or q(z)
q(a) or q(z)  +(a) and if + (z)
+(a) and if + (z)  q(c) or q(z)
q(c) or q(z)  +(c) then + (z)
+(c) then + (z)  +(b). So BQ7 is satisfied. If + (b) ⊆ +(z) then z = b. Since n−(b) = Ø, BQ8 is satisfied.
+(b). So BQ7 is satisfied. If + (b) ⊆ +(z) then z = b. Since n−(b) = Ø, BQ8 is satisfied.
Use Q-model  8 to show that Barbari LQX and others are invalid.
8 to show that Barbari LQX and others are invalid.
Table 19 expresses a Q-model. Suppose +(y) ⊆ n+(z). Then y = b or y = c, and z = c. Since n+(b)  n+(c) and n+(c)
n+(c) and n+(c)  n+(c), BQ3 is satisfied. Since there is no x such that n+(x)
n+(c), BQ3 is satisfied. Since there is no x such that n+(x)  n−(c), BQ5 is satisfied. Since, for every x and y, x
n−(c), BQ5 is satisfied. Since, for every x and y, x  y, BQ4 is trivially satisfied. Suppose + (y) ⊆ q(z). Then y = a and z = b. Then BQ6 is trivially satisfied. Since, for every x, + (x)
y, BQ4 is trivially satisfied. Suppose + (y) ⊆ q(z). Then y = a and z = b. Then BQ6 is trivially satisfied. Since, for every x, + (x)  q(b) or q(x)
q(b) or q(x)  +(b), BQ7 is satisfied. If + (b) ⊆ + (z) then z = b or z = c. Since, for all x, n+(x) does not overlap n−(b) and n+(x) does not overlap n−(c), BQ8 is satisfied.
+(b), BQ7 is satisfied. If + (b) ⊆ + (z) then z = b or z = c. Since, for all x, n+(x) does not overlap n−(b) and n+(x) does not overlap n−(c), BQ8 is satisfied.
Table 20 expresses a Q-model. If + (y) ⊆ n+(z) then y = c and either z = c or z = b. If + (x)  +(c) then x = b or z = c. Since n+(x)
+(c) then x = b or z = c. Since n+(x)  n+(z), BQ3 is satisfied. For every y, if+(y) ⊆ n−(a) then y = c. For every x, if x
n+(z), BQ3 is satisfied. For every y, if+(y) ⊆ n−(a) then y = c. For every x, if x  +(c) then n+(x)
+(c) then n+(x)  n−(a). There are no y such that y ⊆ n−(b). For every y, if +(y) ⊆ n− (c) then y = a. For every x, if x
n−(a). There are no y such that y ⊆ n−(b). For every y, if +(y) ⊆ n− (c) then y = a. For every x, if x  +(a) then n+(x)
+(a) then n+(x)  n−(c). So BQ4 is satisfied. If + (z) ⊆ n+(y) then z = c and either y = b or y = c. n+(x) does not overlap n−(b). If n+(x)
n−(c). So BQ4 is satisfied. If + (z) ⊆ n+(y) then z = c and either y = b or y = c. n+(x) does not overlap n−(b). If n+(x)  n−(c) then x = a or x = b. Since n+(a)
n−(c) then x = a or x = b. Since n+(a)  n−(c) and n+(b)
n−(c) and n+(b)  n−(c), BQ5 is satisfied. For every x and y, if x ⊆ q(y) then x = a and y = b. So BQ6 is trivially satisfied. For all z, if +(z)
n−(c), BQ5 is satisfied. For every x and y, if x ⊆ q(y) then x = a and y = b. So BQ6 is trivially satisfied. For all z, if +(z)  +(a) then z = a or z = b. Since +(a)
+(a) then z = a or z = b. Since +(a)  q(b) and +(b)
q(b) and +(b)  q(b), BQ7 is satisfied. For all z, if + (b) ⊆ +(z) then b = z. Since n−(z) = Ø, BQ8 is satisfied.
q(b), BQ7 is satisfied. For all z, if + (b) ⊆ +(z) then b = z. Since n−(z) = Ø, BQ8 is satisfied.
Table 21 expresses a Q-model. For every x and y, +(x)  n+(y). So BQ3 and BQ5 are satisfied. For all x and y, +(x)
n+(y). So BQ3 and BQ5 are satisfied. For all x and y, +(x)  n−(y). So BQ4 is satisfied. If +(x) ⊆ q(y) and + (y) ⊆ q(z) then x = a and z = c. So BQ6 is satisfied. For every x and y, +(x)
n−(y). So BQ4 is satisfied. If +(x) ⊆ q(y) and + (y) ⊆ q(z) then x = a and z = c. So BQ6 is satisfied. For every x and y, +(x)  q(y) or q(x)
q(y) or q(x)  +(y). So BQ7 is satisfied. If + (x) ⊆ q(y) then x = b or x = c. For all z, n+(b) does not overlap n−(z) and n+(c) does not overlap n−(z). So BQ8 is satisfied.
+(y). So BQ7 is satisfied. If + (x) ⊆ q(y) then x = b or x = c. For all z, n+(b) does not overlap n−(z) and n+(c) does not overlap n−(z). So BQ8 is satisfied.
Table 22 expresses a Q-model. Since BT3 is satisfied, BQ3 and BQ4 are satisfied. Since BT5 is satisfied, BQ5 is satisfied. For every x and y, x  y. So BQ6, BQ7 and BQ8 are trivially satisfied.
y. So BQ6, BQ7 and BQ8 are trivially satisfied.
8.2 Q-valid moods needed for completeness
Aristotle did not discuss any moods with possiblity, as opposed to contingency, premises (or antecedents). But, given the semantics proposed for QLXM’ we must recognize the Q-validity of some moods in which an M-wff is a premise (or an antecedent). In particular Darii QMQ is Q-valid. So, to move in the direction of obtaining completeness results for QLXM’ we shall amend the system by making Darii QMQ axiom 29 (A29).
Theorem 8.18: (soundness of amended QLXM’) Suppose QLXM’ is amended by making the assertion of Darii QMQ,  (QAbc → (MIab → QIac)) be an axiom. Leave everything else unchanged. Then the resulting system is sound.
(QAbc → (MIab → QIac)) be an axiom. Leave everything else unchanged. Then the resulting system is sound.
Proof: Suppose  is a Q-model, V
is a Q-model, V (QAbc) = t and V
(QAbc) = t and V (MIab) = t. Given the definition of a Q-model, at least one of these three conditions is met: i) + (a)
(MIab) = t. Given the definition of a Q-model, at least one of these three conditions is met: i) + (a)  +(b), ii) + (a)
+(b), ii) + (a)  q(b) or iii) +(a) ⊆ n−(b). If i)is met then +(a)
q(b) or iii) +(a) ⊆ n−(b). If i)is met then +(a)  q(c) and thus V
q(c) and thus V (QIac) = t. If ii) is met then +(a)
(QIac) = t. If ii) is met then +(a)  q(c) or q(a)
q(c) or q(a)  +(c) and thus V
+(c) and thus V (QIac) = t. If iii) is met then V
(QIac) = t. If iii) is met then V (MIab) = t and V
(MIab) = t and V (MIab) = f. Given this absurdity V
(MIab) = f. Given this absurdity V (QIac) = t. So
(QIac) = t. So  Q (QAbc → (MIab → QIac)).
Q (QAbc → (MIab → QIac)).
Assertions that are Q-valid correspond to unmarked cells on table 23. The marks in cells indicate how countermodels may be found for the Q-invalid syllogisms the table refers to.
For each unmarked cell we shall show how the indicated syllogism is asserted in the system.
Theorem 8.19: (asserted QMQs and MQQs) The non-numbered QMQ and MQQ cells on table 23 correspond to asserted wffs.
1.  (QAbc → (MIab → QIac)) (Darii QMQ, A29)
(QAbc → (MIab → QIac)) (Darii QMQ, A29)
2.  (QEbc → (MIab → QOac)) (Ferio QMQ, from 1 by CC, AS, CW)
(QEbc → (MIab → QOac)) (Ferio QMQ, from 1 by CC, AS, CW)
3.  (QAbc → (MIba → QIac)) (Datisi QMQ, from 1 by Ap-con, AS)
(QAbc → (MIba → QIac)) (Datisi QMQ, from 1 by Ap-con, AS)
4.  (QAbc → (MAba → QIac)) (Darapti QMQ, from 3 by Ap-con, AS)
(QAbc → (MAba → QIac)) (Darapti QMQ, from 3 by Ap-con, AS)
5.  (QEbc → (MIba → QOac)) (Ferison QMQ, from 3 by CC, AS, CW)
(QEbc → (MIba → QOac)) (Ferison QMQ, from 3 by CC, AS, CW)
6.  (QEbc → (MAba → QOac)) (Felapton QMQ, from 4 by CC, AS, CW)
(QEbc → (MAba → QOac)) (Felapton QMQ, from 4 by CC, AS, CW)
7.  (QAbc → (MAab → QIac)) (Barbari QMQ, from 1 by Ap-sub-a, AS)
(QAbc → (MAab → QIac)) (Barbari QMQ, from 1 by Ap-sub-a, AS)
8.  (QEbc → (MAab → QOac)) (Celaront QMQ, from 7 by CC, AS, CW)
(QEbc → (MAab → QOac)) (Celaront QMQ, from 7 by CC, AS, CW)
9.  (MIbc → (QAba → QIac)) (Disamis MQQ, from 3 by AI, Q-con, CW)
(MIbc → (QAba → QIac)) (Disamis MQQ, from 3 by AI, Q-con, CW)
10.  (MAbc → (QAba → QIac)) (Darapti MQQ, from 3 by Ap-sub-a, AS)
(MAbc → (QAba → QIac)) (Darapti MQQ, from 3 by Ap-sub-a, AS)
11.  (MIcb → (QAba → QIac)) (Dimaris MQQ, from 1 by AI, Q-con, CW, US)
(MIcb → (QAba → QIac)) (Dimaris MQQ, from 1 by AI, Q-con, CW, US)
12.  (MAcb → (QAba → QIac)) (Bramantip MQQ, from 11 by Ap-sub-a, AS)
(MAcb → (QAba → QIac)) (Bramantip MQQ, from 11 by Ap-sub-a, AS)
13.  (MAcb → (QEba → QOac)) (Camenop MQQ, from 12 by CC, AS, CW)
(MAcb → (QEba → QOac)) (Camenop MQQ, from 12 by CC, AS, CW)
Theorem 8.20: (asserted QMMs and MQMs) The non-numbered QMM and MQM cells on table 23 correspond to asserted sentences.
Proof: Use theorem 8.19 and Q-sub-o.
Theorem 8.21: (asserted QLLs and LQLs) The non-numbered QLL and LQL cells on table 23 correspond to asserted wffs.
Proof: Use theorem 8.20 and RV.
Theorem 8.22: (asserted QQMs) The non-numbered QQM cells on table 23 correspond to asserted wffs.
Proof: Use theorem 8.6, Q-sub-o and CW for cells other than Camenes, Fesapo, Celaront and Camenop QQM. For them use the following reasoning.
Table 24 expresses a Q-model. For every x and y, +(x)  n+(y). So BQ3 and BQ5 are trivially satisfied. For every x and y, +(x)
n+(y). So BQ3 and BQ5 are trivially satisfied. For every x and y, +(x)  n−(y). So BQ4 is trivially satisfied. Suppose +(y)
n−(y). So BQ4 is trivially satisfied. Suppose +(y)  q(z). Then y = b and z = c. So BQ6 is trivially satisfied. For every x, + (x)
q(z). Then y = b and z = c. So BQ6 is trivially satisfied. For every x, + (x)  q(b) or q(x)
q(b) or q(x)  +(b). So BQ7 is satisfied. If +(c) ⊆ z then z = c. Since n+(b) does not overlap n−(c), BQ8 is satisfied.
+(b). So BQ7 is satisfied. If +(c) ⊆ z then z = c. Since n+(b) does not overlap n−(c), BQ8 is satisfied.
Table 25 expresses a Q-model. Suppose +(y) ⊆ n+(z). Then y = a and z = c. If+(x)  +(a) then x = a or x = c. Since n+(a)
+(a) then x = a or x = c. Since n+(a)  n+(c), BQ3 is satisfied. Since n−(c) = Ø, BQ5 is trivially satisfied. For every x and y, +(x)
n+(c), BQ3 is satisfied. Since n−(c) = Ø, BQ5 is trivially satisfied. For every x and y, +(x)  n−(y). So BQ4 is trivially satisfied. Suppose +(y) ⊆ q(z). Then y = b and z = c. So BQ6 is trivially satisfied. For all x, +(c)
n−(y). So BQ4 is trivially satisfied. Suppose +(y) ⊆ q(z). Then y = b and z = c. So BQ6 is trivially satisfied. For all x, +(c)  q(x). So BQ7 is satisfied. Since n−(z) = Ø, BQ8 is satisfied.
q(x). So BQ7 is satisfied. Since n−(z) = Ø, BQ8 is satisfied.
Table 26 expresses a Q-model. For every x and y, if +(x) ⊆ n+(y) then x = a and y = c. If +(x)  +(a) then n+(x)
+(a) then n+(x)  n+(c). So BQ3 is satisfied. For every x and y, + (x)
n+(c). So BQ3 is satisfied. For every x and y, + (x)  n−(y). So BQ4 is satisfied. Since n−(c) = Ø, BQ5 is satisfied. For every x and y, if + (x) ⊆ q(y) then y = a or y = c. So BQ6 is trivially satisfied. For every z, z
n−(y). So BQ4 is satisfied. Since n−(c) = Ø, BQ5 is satisfied. For every x and y, if + (x) ⊆ q(y) then y = a or y = c. So BQ6 is trivially satisfied. For every z, z  q(a) or q(z)
q(a) or q(z)  +(a). And for every z, z
+(a). And for every z, z  q(c) or q(z)
q(c) or q(z)  +(c). So BQ7 is satisfied. For every z, if +(a) ⊆ +(z) then z = a. And for every z, if +(c) ⊆ +(z) then z = c. Since n− (a) = Ø and n− (a) = Ø, BQ8 is satisfied.
+(c). So BQ7 is satisfied. For every z, if +(a) ⊆ +(z) then z = a. And for every z, if +(c) ⊆ +(z) then z = c. Since n− (a) = Ø and n− (a) = Ø, BQ8 is satisfied.
Table 27 expresses a Q-model. Since BT3 is satisfied, both BQ3 and BQ4 are satisfied. Since BT5 is satisfied BQ5 is satisfied. Suppose +(y) ⊆ q(z). Then z = b. So BQ6 is trivially satisfied. For all x, x  q(b). So BQ7 is satisfied. If +(b) ⊆ +(x) then x = b. Since n−(b) = Ø, BQ8 is satisfied.
q(b). So BQ7 is satisfied. If +(b) ⊆ +(x) then x = b. Since n−(b) = Ø, BQ8 is satisfied.
Table 28 expresses a Q-model. Suppose +(y) ⊆ n+(z). Then z = c. Since, for all x, n+(x)  n+(c), BQ3 is satisfied. Since n−(c) = Ø, BQ5 is satisfied. Since, for all x and y, +(x)
n+(c), BQ3 is satisfied. Since n−(c) = Ø, BQ5 is satisfied. Since, for all x and y, +(x)  n−(y), BQ4 is trivially satisfied. Suppose +(y) ⊆ q(z). Then y = b and z = a. So BQ6 is trivially satisfied. For all x, x
n−(y), BQ4 is trivially satisfied. Suppose +(y) ⊆ q(z). Then y = b and z = a. So BQ6 is trivially satisfied. For all x, x  q(a). So BQ7 is satisfied. For all x, n−(x) = Ø. So BQ8 is trivially satisfied.
q(a). So BQ7 is satisfied. For all x, n−(x) = Ø. So BQ8 is trivially satisfied.
Note that the acceptance of all but two of the QLM and LQM moods is generated from acceptances involving the MLM and LMM moods.
9 The Aristotelicity of Qlxm’
Of the 154 first, second or third figure syllogisms referred to on table 15 there are exactly thirteen that are Q-valid but invalid for Aristotle. And there are exactly nine that are Q-invalid but are valid for Aristotle. So the Aristotelicity of QLXM’ system is about 86%. Of the twenty-two discrepancies seventeen are due to mistakes involving the use of Reversal. These mistakes are marked on table 14 by using pairs of numbers from 1 to 17. So, for example, on this table both Barbara QXM and Baroco QLX are marked with ‘1’, indicating that by Reversal both should be valid or both should be invalid. But Aristotle regarded only the former as valid. Both Ferison QLM and Camestres LQM are marked with ‘17’, indicating that by Reversal both should be valid or both should be invalid. Aristotle regarded only the former as valid.
So, there are five remaining discrepancies to account for. i) Darapti XQQ: Aristotle could have used Disamis XQQ to show its validity, ii) Darapti LQQ: Aristotle could have used Darapti XQQ to show its validity, iii) Festino QXM: As noted by McCall in [1963, p. 93], Aristotle could have used Festino MXM to show its validity. Given Reversal, Festino MXM is valid in virtue of Disamis XLL. iv) Celarent QLX: Aristotle could have used Reversal and Festino QXM to show it is valid, v) Felapton XQM: Aristotle properly regarded it as valid since he regarded Ferio XQM as valid. Given our interest in developing a formal system that would not have the unAristotelian results, noted in theorem 7.2, which are present in McCall’s Q-L-X-M system, we chose to regard Ferio XQM as Q-invalid.
10 Tally of the Two-Premised Q-Valid Syllogisms
The 333 syllogisms marked on Table 13 are the Q-valid apodeictic two-premised syllogisms in which no contingent wff is a premise or a conclusion. Table 15 and table 23 refer to some of the Q-valid 2-premised syllogisms that involve contingent wffs. To count all of them we need to take account of complementary conversions. Note, for example, that AEA QQQ-figure 1 (that is (QAbc → (QEab → QAac))) is Q-valid by complementary conversion since Barbara QQQ is Q-valid.29 In this section we shall count all of the 2-premised syllogisms that are Q-valid.
When counting the valid moods we shall use ‘[A]’ to mean that the premise or conclusion indicated may be either an A or an E wff. Similarly we shall use ‘[I]’ to mean the premise or the conclusion indicated may be either an I or an O formula. So, by saying that QQQ [A][A][A] in figure 1 is Q-valid, we are claiming the validity of eight figure 1 QQQ syllogisms: QQQ AAA (AAE, AEA, AEE, EAA, EAE, EEA, and EEE). By saying that QXQ [A]I[I] in figure 1 is Q-valid, we are claiming the Q-validity of four figure 1 QXQ syllogisms: QXQ AII (AIO, EII, and EIO).
figure 1: [a][a][a], [a][i][i], [a][a][i]
Figure 1: [A][A]A, [A][A]E, [A][I]I, [A][A]I, [A][A]O
There are 333 + 64 + 40 + 32 + 34 + 20 + 24 + 30 + 46 + 46 + 16 + 16 + 8 + 8 + 8 + 8 + 48 (that is, 781) Q-valid 2-premised syllogisms found in thirty five “general moods”: LLX, LLM, LXX, LXM, XLX, XLM, XXX, XXM, LLL, LXL, XLL, LMM, MLM, MXM, XMM, LMX, MLX, QQQ, QXQ, QLQ, XQQ, LQQ, QXM, XQM, QLX, LQX, QLM, LQM, QMQ, MQQ, QMM, MQM, QLL, LQL, and QQM.
11 Extensions
The most natural extension of the above work on QLXM’ would be to develop a Smiley-type decision procedure for validity for the n-premised syllogisms, for n ≥ 2, where these syllogisms meet the chain condition. Though Smiley’s decision procedure for the assertoric syllogistic pairs inconsistent sets of wffs with syllogisms construed as inferences, the pairing could also be between sets of wffs and syllogisms constructed as implications. The decision procedure would list Q-inconsistent sets such as {P1Ax1x2, P2Ax3x4,…, PnAx2n-1x2n,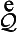 Ax1x2n}, where: i) each Pi, for 1 ≤ i < n, is X, L or Q; ii) Pn is Q; and iii)
Ax1x2n}, where: i) each Pi, for 1 ≤ i < n, is X, L or Q; ii) Pn is Q; and iii)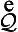 (the negation of Q) is a new quantifier. Given the decision procedure it would follow that (QAab → (Abc → (LAcd → (QAde → QAae)))), for example, is Q-valid.
(the negation of Q) is a new quantifier. Given the decision procedure it would follow that (QAab → (Abc → (LAcd → (QAde → QAae)))), for example, is Q-valid.
Though it is argued above that QLXM’ is more Aristotelian than McCall’s Q-L-X-M there are several other systems that could be developed to bring coherence into Aristotle’s discussions of modalities. For example, consider Barbara XQM. McCall points out that Aristotle’s defense of its validity is flawed, but McCall chooses to take it as an axiom in his Q-L-X-M. It is also an axiom in QLXM’. Dropping this axiom would mean that the semantics for the weaker system would be simpler.
Anderson, Alan Ross, Belnap, Nuel D., Jr., eds. Entailment: The Logic of Relevance and Necessity, volume I. London: Princeton University Press, 1975. and volume II, and 1992
Becker-Freyseng, Albrecht. Die Aristotelische Theorie der äglichkeits-schlüsse:eine logischphilologische Untersuchung der Kapitel 13–22 von Aristoteles Analytica priora I. Princeton: Junker and Dünnhaupt; 1933.
Bell, John L., DeVidi, David, Solomon, Graham. Logical Options: an Introduction to Classical and Alternative Logics. Berlin: Broadview; 2001.
Bochenski, I.M. Ancient Formal Logic. Peterborough: North-Holland; 1963.
Corcoran, John. The completeness of an ancient logic. Journal of Symbolic Logic. 1972;37:696–702.
Cresswell, M.J. Necessity and contingency. Studia Logica. 1988;47:145–149.
Fitting, Melvin, Mendelsohn, Richard L. First-order Modal Logic. Amsterdam: Kluwer; 1998.
In Peter Geach Frege, Gottlob. Negation. In: Black Max, ed. Translations from the Philosophical Writings of Gottlob Frege. second edition. Dordrecht: Blackwell; 1960:117–135.
1964 Geach, P.T. Review of McCall. Ratio. 1963;6:200–206.
Geach, P.T. Logic Matters. Oxford: Blackwell; 1972.
Rod, Girle. Modal Logics and Philosophy. Oxford: McGill-Queen’s University Press; 2000.
Hughes, G.E., Cresswell, M.J. An Introduction to Modal Logic. Montreal: Methuen; 1968.
Hughes, G.E., Cresswell, M.J. A New Introduction to Modal Logic. London: Routledge; 1996.
Johnson, Fred. Models for modal syllogisms. Notre Dame Journal of Formal Logic. 1989;30:271–284.
Fred, Johnson. Three-membered domains for Aristotle’s syllogistic. Studia Logica. 1991;14:181–1870.
Johnson, Fred. Modal ecthesis. History and Philosophy of Logic. 1993;14:171–182.
Johnson, Fred. Syllogisms with fractional quantifiers. Journal of Philosophical Logic. 1994;23:401–422.
Johnson, Fred. Apodeictic syllogisms: Deductions and decision procedures. History and Philosophy of Logic. 1995;16:1–18.
Johnson, Fred. Extended Gergonne syllogisms. Journal of Philosophical Logic. 1997;23:553–567.
Johnson, Fred. Parry syllogisms. Notre Dame Journal of Formal Logic. 1999;40:414–419.
Johnson, Fred. Rejection and truth-value gaps. Notre Dame Journal of Formal Logic. 1999;40:574–577.
Kneale, William, Kneale, Martha. The Development of Logic. London: Clarendon Press; 1962.
Lear, Jonathan. Aristotle and Logical Theory. Oxford: Cambridge University Press; 1980.
Lukasiewicz, Jan. Aristotle’s Syllogistic: From the Standpoint of Modern Formal Logic, second edition. Cambridge: Clarendon Press; 1957.
McCall, Storrs. Aristotle’s Modal Syllogisms. In: Studies in Logic and the Foundations of Mathematics. Oxford: North-Holland; 1963.
Meredith, C.A. The figures and models of the n-termed Aristotelian syllogisms. Dominican Studies. 1953;6:42–47.
Montgomery, H.A., Routley, F.R. Contingency and non-contingency bases for normal modal logics. Logique et Analyse. 1966;35–36:318–328.
Nortmann, Ulrich. Über die Stärke der Aristotelischen Modallogik. Erkenntnis. 1990;32:61–82.
Patterson, Richard. The case of the two Barbaras: basic approaches to Aristotle’s modal logic. Oxford Studies in Ancient Philosophy. 1989;7:1–40.
Patterson, Richard. Conversion principles and the basis of Aristotle’s modal logic. History and Philosophy of Logic. 1990;11:151–172.
Prior, A.N. Formal Logic, second edition. Amsterdam: Clarendon Press; 1962.
Rescher, Nicholas. Aristotle’s theory of modal syllogisms and its interpretation. In: The Critical Approach: Essays in honor of Karl Popper. Oxford: Free Press of Glencoe; 1963.
Ross, W.D. Aristotle’s Prior and Posterior Analytics. New York: Clarendon Press; 1949.
Routley, R., Montgomery, H. On systems containing Aristotle’s thesis. Journal of Symbolic Logic. 1968;33:82–96.
Rumfitt, Ian. The categoricity problem and truth-value gaps. Analysis. 1997;57:223–235.
Smiley, Timothy. On Lukasiewicz’s Ł-modal system. Notre Dame Journal of Formal Logic. 1961;2:149–153.
Smiley, Timothy. What is a syllogism. Journal of Philosophical Logic. 1973;2:136–154.
Smiley, Timothy. Aristotle’s completeness proof. Ancient Philosophy. 1994;14:25–38.
Smiley, Timothy. Rejection. Analysis. 1996;56:1–9.
Smith, Robin. What is Aristotelian ecthesis? History and Philosophy of Logic. 1982;3:113–127.
Hackett, Indianapolis Smith, Robin, Aristotle, Prior Analytics, 1989.
Sugihara, T. Necessity and possiblity in Aristotelian syllogistic. Memoirs of the Faculty of Liberal Arts, Fukui University. 1957;6:75–87.
Sugihara, T. Necessity and possiblity in Aristotelian syllogistic. Memoirs of the Faculty of Liberal Arts, Fukui University. 1957;7:15–22.
Thom, Paul. The two Barbaras. History and Philosophy of Logic. 1991;12:135–149.
Thom, Paul. Apodeictic ecthesis. Notre Dame Journal of Formal Logic. 1993;34:193–208.
Thom, Paul, Interpreting Aristotle’s contingency-syllogistic. Taylor, C.C.W., eds. Oxford Studies in Ancient Philosophy, volume 12. Clarendon Press: Oxford, 1994:91–109.
Thom, Paul, The Logic of Essentialism: An Interpretation of Aristotle’s Modal Syllogistic. The New Synthese Historical Library. Kluwer: Oxford, 1996.
Thomason, S.K. Semantic analysis of the modal syllogistic. Journal of Philosophical Logic. 1993;22:111–128.
Thomason, S.K. Relational models for the modal syllogistic. Journal of Philosophical Logic. 1997;26:129–141.
van Rijen, Jeroen. Aspects of Aristotle’s Logic of Modalities. Dordrecht: Reidel; 1989.
von Wright, G.H. An Essay in Modal Logic. Dordrecht: North-Holland; 1951.
1In [1964] P. T. Geach prefers ‘plain’ over ‘assertoric’.
2The manner of presentation of this system is heavily influenced by Hughes and Cresswell’s presentations of various systems in [1996].
3‘Cut’ is also used to refer to these rules.
4‘Transitivity’ and ‘Hypothetical syllogism’ are also used to refer to the first of these two rules.
5I. M. Boche ski, on p. 212 of [1963], states that the “law of accidental conversion of the universal negative is not in Aristotle”. He is not saying that Aristotle considered inference ii) to be invalid.
ski, on p. 212 of [1963], states that the “law of accidental conversion of the universal negative is not in Aristotle”. He is not saying that Aristotle considered inference ii) to be invalid.
6This rule is discussed, but not named, on p. 29 of [Hughes and Cresswell, 1996].
7Smiley, in his influential article [1996], points out that Carnap and Łukasiewicz were the first logicians to formalize the notion of rejection. Smiley attributes the shunning of rejection by most logicians to Frege’s [1960]. Smiley effectively argues that Frege’s rejection of rejection, using Occam’s razor, was unfortunate, and Smiley shows how rejection may be put to good use in ways other than those envisioned by Carnap or Łukasiewicz. For recent work on rejection that is stimulated by Smiley’s article see [Rumfitt, 1997] and [Johnson, 1999b].
8In the above passage Aristotle uses the semantic counterpart of this two-stage syntactic process. First, he shows by his counterexample that {Aba, Ecb, Aca} and {Aba, Ecb, Eca} are semantically consistent, from which it follows that neither of the particulars Oca and Ica is a semantic consequence of {Aba, Ecb}. Secondly, since the universal claims Eca and Aca are stronger than Oca and Ica, respectively, they cannot be a semantic consequence of {Aba, Ecb}. Aristotle is using what W. D. Ross [1949, p. 302] calls a “proof by contrasted instances,” to show a pair of premises is, in Jonathan Lear’s [1980, p. 54] terms, “semantically sterile”.
9See [1961] for Smiley’s extensions of Łukasiewicz’s work on ŁM.
10[Hughes and Cresswell, 1968, pp. 29–30] for a discussion of this sentence, an axiom in Robert Feys’s System T.
11For recent books that contain sections on modal predicate logic see [Hughes and Cresswell, 1996], [Fitting and Mendelsohn, 1998], [Girle, 2000] and [Bell et al., 2001].
12See [Boche ski, 1963, pp. 57–62] for a useful discussion of Becker’s work.
ski, 1963, pp. 57–62] for a useful discussion of Becker’s work.
13In [Johnson, 1993] Aristotle’s proofs by ecthesis are treated as essentially proofs by Existential Instantiation. For alternative accounts of proofs by ecthesis see [Thom, 1993] and [Smith, 1982].
14Paul Thom in [1991] argues that Aristotle made a mistake in regarding Bocardo LXL as valid. Thom contrasts his views with those in [Johnson, 1989], [Patterson, 1989], [Patterson, 1990] and [van Rijen, 1989].
15Correction: on p. 273 of [1989] change → LAac in *5.3 to → Aac.
16For example, I borrow Thom’s use of “base conditions” and “superstructural conditions” to present what he calls a “two-layered semantics”. And I borrow Thomason’s use of “VM” to refer to a valuation relative to a model.
17Thomason [1993, p. 127] uses this table to invalidate Baroco XLL and Bocardo LXL though his definition of “validity” is not identical to that which we are currently discussing. Thomason models are discussed below.
18[Johnson, 1991] shows that W does not require more than 3 members if all simple sentences are assertoric and all terms are “chained”.
19The systems proposed by [Łukasiewicz, 1957], [Corcoran, 1972] and [Smiley, 1973] do not attempt to accommodate Aristotle’s proofs by ecthesis. According to Thom’s [Thom, 1991] account of ecthesis both Baroco XLL and Bocardo LXL are valid, though Aristotle regarded them as invalid.
20For an alternative method of working with singular sentences in the context of syllogistic reasoning see [Johnson, 1999a].
21It is very surprising that Aristotle is scarcely mentioned in [Anderson and Belnap, 1975 and 1992], which provides authoritative discussions of relevance logic. See McCall’s discussion of “connexive implication” [1975 and 1992, pp. 434–452] for the one reference to Aristotle. In [Johnson, 1994] a syllogistic logic is developed that is a “connexive logic”. Pleasing relevance logicians, the logic satisfies both Aristotle’s thesis (If y is the logical consequence of a non-empty set of premises, X, then X is semantically consistent) and Boethius’s Thesis (If z is the logical consequence of a set of premises, X ∪ y, then z is not the logical consequence of a set of premises X ∪ y′, where y′ contradicts y). Ironically, neither Aristotle’s nor Boethius’s thesis holds for what is now known as the “classical propositional calculus”. In [Johnson, 1994] a theorem is proven that has as a corollary this interesting result due to C. A. Meredith in [1953]: The number of valid n-premised assertoric syllogisms (for n ≥ 2) is 3n2 + 5n + 2. There is no question that in Chapter 25 of Book I of the Prior Analytics Aristotle was looking for such a general result. Given the chain condition such counts are possible.
22Corcoran gives a Henkin-style completeness proof for the assertoric syllogistic. His system validates inferences such as ‘Eab; so Ace’, inferences eschewed by relevance logicians. This inference is valid for Corcoran since the conclusion is logically true, even though the premise is irrelevant to the conclusion.
23See [Johnson, 1994] and [Johnson, 1997] for other systems that yield Smiley’s decision procedure as a special case of a more general decision procedure.
24The following symbols are also found in the literature that formalizes contingency: ‘E’2 [Becker-Freyseng, 1933], ‘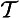 ’ [Łukasiewicz, 1957] and ‘P()’ [Smith, 1989]. Smith’s P(Aab) is McCall’s QAab, and Smith’s PAab is McCall’s MAab. Łukasiewicz used ‘
’ [Łukasiewicz, 1957] and ‘P()’ [Smith, 1989]. Smith’s P(Aab) is McCall’s QAab, and Smith’s PAab is McCall’s MAab. Łukasiewicz used ‘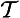 ’ instead of ‘Q’ since earlier in his book he used ‘Q’ for ‘is equivalent to’. McCall’s Barbara LQM is Ross’s [1949] An Ac Ap. Montgomery and Routley use xdtri; for contingency in [1966] and [1968]. And Cresswell uses
’ instead of ‘Q’ since earlier in his book he used ‘Q’ for ‘is equivalent to’. McCall’s Barbara LQM is Ross’s [1949] An Ac Ap. Montgomery and Routley use xdtri; for contingency in [1966] and [1968]. And Cresswell uses 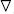 for contingency and
for contingency and  for non-contingency in [1988].
for non-contingency in [1988].
25On p. 198 of [1957] Łukasiewicz calls Aristotle’s view a ‘grave mistake’. Łukasiewicz says ‘He [Aristotle] does not draw the right consequences from his definition of contingency, and denies the convertibility of universally-negative contingent propositions, though it is obviously admissible.’ But, following McCall, one can attempt to formulate Aristotle’s contingency syllogistic without, in effect, defining QEab as (¬LEab ∧ ¬L¬Eab).
26Thom evaluates QOab in this way in [1993] and [1994].
27In the notes for table 12 McCall comments on tables in [Becker-Freyseng, 1933, p. 88] and [Ross, 1949, after p. 286].
28As noted above, BQ5 is a weaker condition than BT5. Replacing BQ5 with BT5 in the definition of a Q-model, forming a Q’ model, yields this highly unAristotelian result:  Q′, (QAab → Eab). For, suppose that for some Q′-model M, V
Q′, (QAab → Eab). For, suppose that for some Q′-model M, V (Eab) = f. Then V
(Eab) = f. Then V (Iab) = t. By S2 and BT5, +(a)
(Iab) = t. By S2 and BT5, +(a)  n+(b). By S9, V
n+(b). By S9, V (QAab) = f.
(QAab) = f.
29See Ross’s table in [1949, facing p. 286] for references to this as well as several other syllogisms that may be validated by using complementary conversion.