ANSWER EXPLANATIONS
Elite Questions for the SAT Reading Test
1. D
This passage is best described as a nontechnical discussion of a problematic way of thinking. The problematic way of thinking at the heart of the passage is the failure of many people to develop an appreciation of common large numbers (lines 1–2) and the correspondingly small probabilities associated with them (lines 27–28). This discussion is best described as nontechnical because it does not rely on any technical expertise or use any technical jargon; in fact, it uses several devices of popular exposition, such as humor and personal anecdote. Choice A is incorrect because the passage does not discuss any specific solutions to the problem of innumeracy. Choice B is incorrect because, although the author does mention a personal experience in the final paragraph, this does not serve as the focus of the passage as a whole. Choice C is incorrect because the passage is not focused on any particular policy, let alone any dangerous ones.
2. D
The question in lines 51–53 (“But with...that way?”) indicates that determining the precise mechanisms behind the origin of life is an intractable mystery, because we can’t travel back in time. Choice A is incorrect because although the question raises a doubt, it does not present refuting evidence. Choice B is incorrect because experiment cannot address the problem it indicates. Choice C is incorrect because it does not imply that scientists are confused about the matter.
3. C
The statement that astrophysicists can now trace the building blocks of life—carbon, nitrogen, and oxygen—to a spectacular birth inside ancient exploding stars (lines 58–61) directly implies that the origins of life are even deeper than we thought—that is, we have to look even further into the past than the times of the early Earth (line 46) to find the most basic building blocks of life. Choice A is incorrect because neither this paragraph nor the passage as a whole suggests that there is a possibility of extraterrestrial life. Choice B is incorrect because the power of scientific tools is not discussed. Choice D is incorrect because the elemental components listed are not complex molecules at all.
4. D
The main purpose of the passage is to present the hypothesis that Homo sapiens came to dominate Homo neanderthalensis because the physical frailty of humans forced them to exploit their intelligence. Choice A is incorrect because, although the passage does mention some unique features of Neanderthals, those features are not the focus of the passage. Choice B is incorrect because, although the diagram does indicate the common lineage of modern humans and Neanderthals, the passage does not explain their common origins. Choice C is incorrect because, although the passage does discuss spoken language in humans, it also indicates that this skill did not provide humans with an advantage over Neanderthals.
5. A
The central idea of the passage, as illustrated by the analogy given in the final paragraph, is that Homo sapiens came to dominate Neanderthals because we were able to take advantage of the need to exploit our minds (lines 45−46), giving us an evolutionary pathway that was denied to Neanderthals. Choice B is incorrect because, although the passage clearly states that Neanderthals may in fact have had the larger [brains] (lines 21−22), the analogy in the final paragraph does not suggest that this was an encumbrance to them. Choice C is incorrect because, although the passage states that Neanderthals were stronger than us (line 46) and could survive with their physical strength (lines 47–48), the central point of the analogy is that this physical superiority was not enough to help them survive to modern times. Choice D is incorrect because the previous paragraph makes it clear that the distinct advantage of Homo sapiens did not necessarily involve verbal language skill.
6. B
This passage is best described as a description of a useful mode of reasoning (specifically, “mechanistic explanation”) followed by caveats about its use. It begins by describing intellectual progress (line 1) as a journey from teleological to mechanistic explanation (lines 3–4), but then goes on to discuss the caveat that even the most scientific among us [are] still plagued by faulty intuitions (lines 11–12) as we try to apply this mode of reasoning. Choice A is incorrect because the evolution from teleological to mechanistic explanations is not framed in terms of any historical debate, and although this evolution is discussed in the context of explaining scientific phenomena like sunshine, rainfall, and fluid dynamics, this is done consistently throughout the passage and is not therefore part of any developmental progression. Choice C is incorrect because the essay is about the nature of different kinds of explanation, not the explanation of any particular phenomenon. Choice D is incorrect because, although the essay as a whole might be regarded somewhat as a refutation of teleological explanation (and an affirmation of mechanistic explanation), it does not characterize teleological explanation as a misconception, but rather as a widely used mode of reasoning that is flawed but has conversational utility.
7. C
In the second paragraph (lines 16–30), Kandinsky discusses the situation in which a revival of the external forms (lines 23–24) of a previous era can be achieved when there is a similarity of inner tendency in the whole moral and spiritual atmosphere (lines 18–20) of the two eras. In lines 25–30, Kandinsky states that [an] example of this today is our sympathy with the Primitives… [who, like] ourselves, … sought to express in their work only internal truths, renouncing in consequence all considerations of external form. In short, the revival of the external forms (lines 23–24) sought by the primitivists of Kandinsky’s era could not be achieved by considerations of external form (line 30). The similarity of form therefore is incidental rather than intentional. Choice A is incorrect because at no point in the passage does Kandinsky suggest that the Primitivist
movement is inevitable. Choice B is incorrect because Kandinsky indicates that the Primitivist movement can only be of short duration (line 52). Choice D is incorrect because Kandinsky indicates that those who try to follow the Greek methods (lines 8–9) create works that are not profound, but remain soulless for all time (line 10).
8. B
As indicated in the explanation given in the previous answer, the best evidence is in lines 27–30.
Elite Questions for the SAT Writing and Language Test
9.
The main verb is the sixth word in the sentence. To understand this sentence, we need to know that B/buffalo has three distinct meanings: (1) Buffalo (adj) is an adjective describing people or things from Buffalo, a city in New York; (2) to buffalo (v) means to intimidate; and (3) buffalo (n) are large wild oxen. We can also understand this sentence better by inserting some implied words: [The] Buffalo buffalo [that] Buffalo buffalo buffalo buffalo [the] Buffalo buffalo [that] Buffalo buffalo buffalo. The translation is The oxen from Buffalo that are intimidated by other oxen from Buffalo intimidate oxen from Buffalo that are intimidated by other oxen from Buffalo. (Chapter 5, Lesson 2: Parsing Sentences)
10. A
The original phrasing is correct. The pronoun themselves serves as an emphatic appositive (Lesson 12) and the verb were agrees with the plural subject surgeons and coordinates logically with the past tense verb assumed. Choice B is incorrect because they cannot serve as an appositive adjective. Choices C and D are incorrect because the present tense are does not coordinate logically with the past tense assumed. (Chapter 5, Lesson 12, Pronoun Case; Chapter 5, Lesson 4: Verb Agreement)
11. C
In order for sentence 5 (They promote “engagement” rather than empowered and critical thought) to make sense, its subject, they, must have a clear and logical antecedent. Of the options, only choice C provides a logical antecedent: online conversations. None of the other options provides a logical and unambiguous antecedent for this subject. (Chapter 5, Lesson 5: Developing and Coordinating Ideas; Chapter 5, Lesson 6: Transitions and References)
12. B
The second clause of the sentence, we will achieve our goal, is in the indicative mood, therefore the conditional clause should be in the indicative mood also, as in choice B. (Chapter 5, Lesson 17: Verb Mood)
13. B
The underlined portion must logically coordinate the main ideas of the two sentences. The first sentence states that low interest rates usually encourage businesses to take out loans. The second sentence, in contrast, indicates a situation in which low interest rates would not necessarily lead to increased borrowing. Since the two ideas contrast each other, the most logical coordinator is B, however. (Chapter 5, Lesson 6: Transitions and References)
14. D
A colon before an independent clause indicates that this clause explains the one preceding it. In choices A, C, and D, the clause after the colon is the same: our experiences affect our priorities and deepest values. What does this explain? It does not explain the fact that our principles motivate us, so choices A and C are incorrect. It does, however, explain how our principles can change, so D provides a logical phrasing. Choice B is incorrect because the fact that our principles often motivate us does not explain the fact that our experiences affect our priorities. (Chapter 5, Lesson 18: Punctuation)
15. B
The first two sentences describe a problem that has impeded biological research, and the third sentence describes a breakthrough that has solved the problem. Choice A, Fittingly, is incorrect because nothing in this paragraph indicates that the “clean room” solution is any more appropriate to the context than any other solution. Choice C, In turn, is incorrect because nothing indicates that the solution arose from an exchange or logical sequence of events. Choice D, Accordingly, is incorrect because nothing indicates that this solution corresponds to or results from any defined situation. Choice C is best because it is certainly fortunate to find a solution to a long-standing problem. (Chapter 5, Lesson 5: Developing and Coordinating Ideas; Chapter 5, Lesson 6: Transitions and References)
16. D
The subject and verb of this sentence is The (disappointing) thing was—. Therefore, the underlined portion should be a noun phrase, and not an independent clause. Therefore, choices A and B are incorrect. Choice C is incorrect because the pronoun they lacks a logical antecedent and the verb should not take the subjunctive mood. (Chapter 5, Lesson 2, Parsing Sentences; Chapter 5, Lesson 11: Pronoun Agreement; Chapter 5, Lesson 17: Verb Mood)
17. D
Choice A is incorrect because the adjective phrase that starts the sentence does not logically modify the subject of the sentence: a musical culture can’t be famous for its visual and performing arts scene. Choice B is incorrect because its lacks a logical antecedent. Choice C is incorrect because the sentence is not grammatical after the interrupting modifier has been trimmed. Choice D is best because it coordinates the two ideas logically and grammatically. (Chapter 5, Lesson 11: Pronoun Agreement; Chapter 5, Lesson 9: Using Modifiers Logically; Chapter 5, Lesson 5: Developing and Coordinating Ideas)
18. A
The original phrasing is best, even if it sounds strangely formal. The phrase need not is equivalent to do not need to. Choice B is redundant, because need to and have to are essentially synonyms. Choice C is wordy and implies illogically that plays can have human needs. Choice D is not idiomatic. (Chapter 5, Lesson 17: Verb Mood; Chapter 5, Lesson 15: Idiomatic Expression)
19. D
This sentence has an inverted syntax (Lesson 4), and the sentence can be parsed logically only if the underlined phrase is a noun or noun phrase that serves as the subject of the sentence. Choices C and D both provide gerundive (Lesson 7) noun phrases as subjects, but only choice D creates a logical and parallel comparison when “un-inverted”: Having to watch for avalanches at high altitudes was even more taxing than climbing without supplemental oxygen. (Chapter 5, Lesson 3: Trimming Sentences; Chapter 5, Lesson 7: Parallelism)
20. C
Choices A and D are incorrect because both commit comma splices, joining independent clauses with only a comma. Choice B is incorrect because which illogically refers to the vote, but clearly it is the delay that fueled resentment, not the vote. Choice C clarifies the source of the resentment. (Chapter 5, Lesson 18: Punctuation; Chapter 5, Lesson 11: Pronoun Agreement)
21. C
The original phrasing is incorrect because her’s is not a valid word. The two third-person singular feminine possessive pronouns in English are her (adj) and hers (n): her’s is not an acceptable construction. Choices B and D are incorrect because the context requires a possessive. Choice C provides a correct use of the possessive. (Chapter 5, Lesson 18: Punctuation; Chapter 5, Lesson 12: Pronoun Case)
22. A
Although the main clause is discussing a work of literature, it is making a historical claim about one of Jules Verne’s predictions, and therefore the main verb takes the historical past tense, predicted, rather than the artistic present. The underlined phrase indicates a fact that we might call retro-consequential: a future event (rather than a previous one) extends a consequence to a status. The proper form for this kind of “future-in-the-past” aspect is would not be invented, as in choice A. Choice B is incorrect because it uses the consequential aspect, which applies to a previous event rather than to a future one. Choice C is incorrect because it uses a subjunctive form, but the statement is not counterfactual or hypothetical. Choice D is incorrect because it uses the simple future tense, which is illogical in this context. (Chapter 5, Lesson 13: Verb Tense and Aspect; Chapter 5, Lesson 17: Verb Mood)
23. D
The sentence requires a verb that describes what blowback (unintended adverse results of a political action) does with regard to provocative comments. Choice A is incorrect because derive requires an indirect object and the preposition from, so this is an unidiomatic usage. Choice B is incorrect because blowback cannot pursue (chase). Choice C is incorrect because to advance is to move forward in a purposeful way, but blowback is unintended and negative. Choice D is correct because it is reasonable to expect that blowback would ensue (happen as a result) after provocative comments. (Chapter 5, Lesson 1: Writing and Language Question Types; Chapter 5, Lesson 5: Developing and Coordinating Ideas)
24. C
The core of this sentence is The reason is—. Therefore, the object in this clause must be a noun phrase that defines the reason. Choices A and D are incorrect because a phrase that begins with because is not a noun phrase. Choice B is incorrect because to perpetuate means to make (something) continue indefinitely, which is not what good marathon runners want to do with their pace. They only want to keep a steady pace until the end of the race. (Chapter 5, Lesson 1: Writing and Language Question Types; Chapter 5, Lesson 2: Parsing Sentences)
25. B
When you want to specify the primary function (a noun) that some device serves, the proper idiom is serves as (an object or action that serves that function). You may use the idiom serves (infinitive) if the infinitive specifies the purpose, as in This letter serves to notify you that…. However, the infinitive to be does not specify a purpose, so choice A is incorrect. Choice C is unidiomatic. Choice D is incorrect because the idiom serves for is used to indicate a period of service, as in Charles served for 12 years as a State Representative. (Chapter 5, Lesson 15: Idiomatic Expression; Chapter 5, Lesson 7: Parallelism)
26. A
The original provides the correct imperative phrasing. Since the verb suggested already indicates a command or suggestion, no auxiliary is necessary and the verb indicating the suggestion should use the infinitive form. Choice B is incorrect because it uses the indicative mood rather than the imperative mood. Choice C is incorrect because the auxiliary should is redundant, and the subject does not align with the parallel predicate that follows the underlined portion. Choice D is incorrect because its subject does not align with the parallel predicate that follows the underlined portion: our investments should not automate monthly transfers, but rather we should. (Chapter 5, Lesson 17: Verb Mood; Chapter 5, Lesson 7: Parallelism)
27. A
The original punctuation is correct. The title in quotes is an appositive title, and should be separated from the noun it modifies, woodcut, with a comma. In choice B, the comma is incorrect because it disrupts the participial phrase titled “Blue Things 1963-1970.” In choice C, the first comma serves no grammatical purpose. In choice D, the colon does not belong because it does not introduce an explanatory clause, specifier, or list. Notice that providing the name of the woodcut does not specify it, because the phrase Blackburn’s woodcut includes no indefinite determiner (a or an), and already refers specifically to “Blue Things 1963-1970.” (Chapter 5, Lesson 18: Punctuation)
Elite Questions for the SAT Math Test — No Calculator
28. A
You might approach this question by setting each expression equal to 1 and see if you can find a solution. For instance, you might start with choice A:
So, it seems that the first expression must equal 1 if b = 0, right? No! Proving that if A is true, then B is true is NOT the same thing as proving that if B is true, then A is true. Notice that if you plug b = 0 back into the expression, you get 0/0, which is undefined!
We can see why this expression can never equal 1 by distributing the division: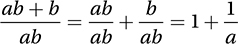 
But since 1/a can never equal zero (because its numerator is never 0), this expression can never equal 1! Notice that choice B equals 1 when a = 1 and b = 0, choice C equals 1 when a = 1 and b = 1, and choice D equals 1 when a = 3 and b = 1. Therefore, the correct answer is A. (Chapter 6, Lesson 3: Simplifying Expressions)
29. D
There is no need to do a lot of algebra here (which can be a bit tricky). Keep in mind that absolute values are never negative. Therefore, choice C can’t have a solution because a negative divided by a positive must be negative, and a negative can’t be greater than 1/2. It shouldn’t be hard to guess-and-check solutions for the other statements. For instance, x = 12 is a solution to both A and B, and x = 0 is a solution to D. (Chapter 6, Lesson 8: Absolute Values)
30. B
We just need to use the formula for the slope of a line and solve it for c.
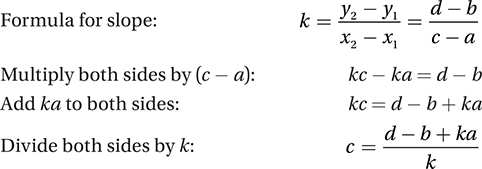
Therefore, the correct answer is B. (Chapter 6, Lesson 5: Constructing and Interpreting Linear Equations; Chapter 6, Lesson 7: Analyzing Linear Graphs)
31. D
There are several ways to approach this question, but perhaps the most straightforward is to use the slope formula to calculate the slope of the line that contains each point in the choices, and see which gives a slope that is outside the given range:
A)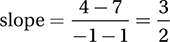 
B)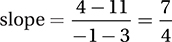 
C)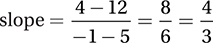 
D)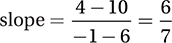 
Since 
is less than 1, the correct answer is D. (Chapter 7, Lesson 5: Constructing and Interpreting Linear Equations)
32. B
There is no need to do any calculation here. The mean of a distribution is its “center of mass” and the standard deviation is a measure of its “spread.” If you imagine rearranging the data for Class 1 so that it looks like the data for Class 2, you can see that you would have to move a bunch of points to the right. This means that the “center of mass” has moved to the right and therefore m1 < m2. It should also be clear by inspection that the data for Class 2 are more “bunched up” around the mean than are the data for Class 1, and so s1 > s2. (Chapter 7, Lesson 1: Averages; Chapter 7, Lesson 3: Data Spread)
33. C
Since the ratio of black marbles to white marbles is 9:14, we can say that the number of black marbles is 9n and the number of white marbles is 14n, where n is some positive integer. In other words, the number of black marbles is a multiple of 9 and the number of white marbles is a multiple of 14. Similarly, since the ratio of white marbles to red marbles is 18:13, the number of white marbles can be expressed as 18m and the number of red marbles can be expressed as 13m, where m is also positive integer. Since the number of white marbles must be both a multiple of 14 and a multiple of 18, the least possible number of white marbles is 126, which is the least common multiple of 14 and 18. (This is because 14 = (2)(7) and 18 = (2)(3)(3), so the smallest number with all the necessary factors is (2)(3)(3)(7) = 126.) This means that n = 9 and m = 7, so there are at least 9n = 9(9) = 81 black marbles and 13m = 13(7) = 91 red marbles. Therefore, the least possible number of marbles altogether is 126 + 81 + 91 = 298, and the correct answer is C. (Chapter 6, Lesson 1: Word Problems; Chapter 7, Lesson 6: Ratios)
34. A
Therefore, the correct answer is A. (Chapter 7, Lesson 9: Proportions and Scaling; Chapter 8, Lesson 4: Analyzing and Factoring Quadratics)
35. C
We can systematically complete the table by starting with the fact that there are 200 students in total. Since 125 of these students attend public colleges, 200 − 125 = 75 attend private colleges, and of these, 75 − 20 − 30 = 25 attend medium-sized private colleges. Also, 200 − 75 − 100 = 25 students attend small colleges, and therefore 25 − 20 = 5 of these attend small public colleges. Since 100 students attend large colleges, 100 − 30 = 70 attend large public colleges. Therefore, 125 − 70 − 5 = 50 students attend medium-sized public colleges. The completed table should look like this:
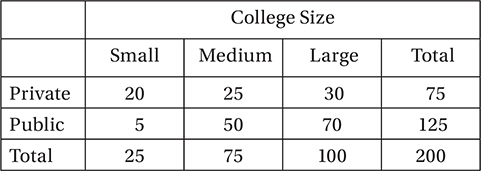
This means that 50 of the 75 students attending medium-sized colleges are attending public colleges, so this fraction is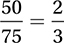 
. (Chapter 7, Lesson 10: Tables and Venn Diagrams; Chapter 7, Lesson 11: Conditional Probabilities from Tables)
36. B
A zero of a function is a value of x for which the function equals zero. Let’s define m as the missing zero. If the zeros of this quadratic are 9 and m, then according to the
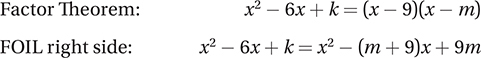
Since the left and right sides of this equation must be identical quadratics, the coefficients must match and so m + 9 = 6 and therefore m = −3. (Chapter 8, Lesson 4: Analyzing and Factoring Quadratics)
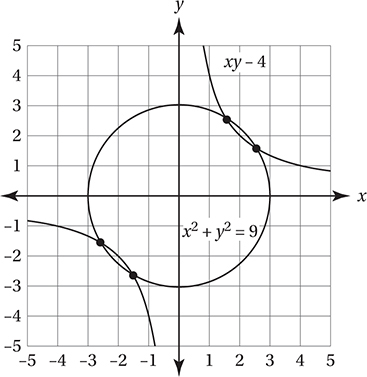
37. A
By direct substitution of x = 3 and consulting the graph, we get
A) g(3) = f(3 + 2) = f(5) = 0
B) g(3) = f(3 − 2) = f(1) = 2
C) g(3) = f(3) + 2 = 0 + 2 = 2
D) g(3) = f(3) − 2 = 0 − 2 = −2
Therefore, the correct answer is A. (Chapter 8, Lesson 1: Functions; Chapter 8, Lesson 2: Representing Functions)
38. D
If the vertex of the parabola is (3, −4), its axis of symmetry is x = 3. This means that the average of the zeros of the function must be 3. Since each quadratic function is given in factored form, we can use the Zero Product Rule to find the zeros of each function:
A) zeros: x = −3, x = 4; average of zeros: 1/2
B) zeros: x = 3, x = −4; average of zeros: −1/2
D) zeros: x = 1, x = 5; average of zeros: 3
Since both choices C and D have an axis of symmetry of x = 3, we must check to see which contains the point (3, −4). Substituting x = 3, we get
C) y = (3 − 2)(3 − 4) = (1)(−1) = −1
D) y = (3 − 1)(3 − 5) = (2)(−2) = −4
Therefore, the correct answer is D. (Chapter 8, Lesson 6: Analyzing Graphs of Quadratic Equations)
39. D
Since this quadratic equation is in the form ax2 + bx + c = 0, there is no need to find both solutions in order to find their sum. We can just use the fact that the sum of the solutions to any quadratic equation in standard form is −b/a. In this case, −b/a = −(−8)/3 = 8/3, and so the correct answer is D. (Chapter 8, Lesson 5: Solving Quadratic Equations)
40. B
The solution is the “overlap” of these three inequalities. All three are satisfied only if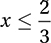 
, choice B.
(Chapter 6 Lesson 9: The Laws of Inequality)
41. C
The center of the circle is the midpoint of the diameter, so the center is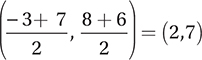 
. This means that the equation has the form (x − 2)2 + (y − 7)2 = r2, where r is the radius of the circle. Although we could find r by using the Distance Formula to find the distance from the center to one of the points on the circle, it is simpler to plug in either set of coordinates of the given points on the circle to find r2.
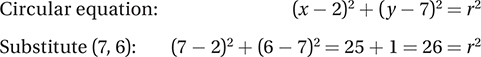
(Notice that substituting (−3, 8) gives the same result.)
Therefore, the equation is (x − 2)2 + (y − 7)2 = 26. (Chapter 9, Lesson 5: Circles)
42. 6
This system is nonlinear, so graphing the equations is a nightmare and solving the system algebraically is insane. But this question can still be solved simply by applying the Law of Combination.
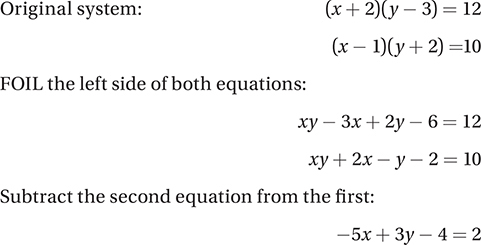
(Chapter 6, Lesson 11: Linear Systems; Chapter 6, Lesson 12: Solving Systems with Algebra)
43. 7
Both inequalities can be expressed as “sandwich” inequalities. For instance, |5a − 2| ≤ 8 can be expressed as
Since the greatest a can be is 2 and the least b can be is −5, the greatest possible value of a − b is 2 − (−5) = 7. (Chapter 6, Lesson 8: Absolute Values; Chapter 6, Lesson 9: The Laws of Inequality)
44. 12
You might start by substituting x = 2 and y = 14 into the function and seeing where it gets you.
Unfortunately, this leaves us with two unknowns, so we can’t solve for b just yet.
In order for the graph of this function to be linear, the denominator (x + 2) must be a factor of the numerator so that the two can “cancel” if x ≠ −2, to give a “first degree polynomial,” that is, a linear function. In other words, the function must be of the form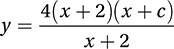 
, which, when x ≠ 2, is equivalent to y = 4(x + c). Now when we substitute the point (2, 14) we get
This means that a = 14 and b = 12. (Notice that these values confirm our first result that 2a + b = 40.) (Chapter 6, Lesson 3: Simplifying Expressions; Chapter 6, Lesson 5: Constructing and Interpreting Linear Equations)
BONUS: Why does the question specify that x must be greater than 0 ?
45. B.
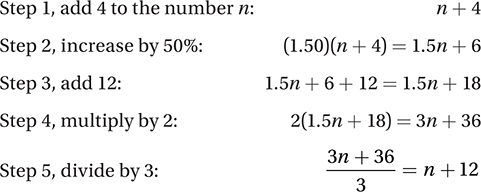
Since g is equivalent to adding 12, which is Step 3, the correct answer is B. (Chapter 8, Lesson 1: Functions)
46. C
For convenience, let’s define a new variable, z = x/2. Doubling both sides gives us x = 2z. If we use these equations to substitute into the original functions, we get f(z) = 2z + 1 and g(z) = 2z − 1. Since the name of the input variable doesn’t matter, this means that f(x) = 2x + 1 and g(x) = 2x − 1. Therefore, f(g(x)) = f(2x − 1) = 2(2x − 1) + 1 = 4x − 2 + 1 = 4x − 1 and so the correct answer is C. (Chapter 8, Lesson 1: Functions; Chapter 8, Lesson 3: Compositions and Transformations)
47. B
48. 15
By the definition of tangent,
Alternately, you might notice that the triangle BCE has sides in a 3-4-5 ratio. (Chapter 9, Lesson 9: Basic Trigonometry)
49. C
(Chapter 8, Lesson 10: The Laws of Exponentials)
BONUS: If the exponent in the first equation were changed from 12 to 24, but everything else about the question remained the same, this question would have no solution. Why not?
50. C
We can use direct substitution in the table to evaluate g(f(h(x))) for the values of x in the choices.
A) g(f(h(2))) = g(f(1)) = g(2) = −6
B) g(f(h(3))) = g(f(2)) = g(4) = 0
C) g(f(h(4))) = g(f(3)) = g(6) = 6
D) g(f(h(5))) = g(f(4)) = g(8) = 12
The only choice that gives an output of 6 is C. (Chapter 8, Lesson 3: Compositions and Transformations)
51. 43
Since ABCD is a parallelogram, angles ADB and DBC form an alternate interior pair (also known as a “Z” pair), and so they have equal measures.
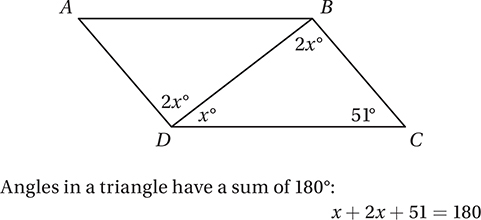
(Chapter 9, Lesson 1: Angles and Parallel Lines; Chapter 10, Lesson 2: Triangles)
52. A
The median of a set of 20 numbers is the average of the 10th greatest and 11th greatest numbers. Since only the 1st and the 20th greatest numbers have been changed, and the relative position of these two numbers in the set remains the same, the median of the new set must equal the median of the old set.
However, increasing the greatest number and decreasing the least number in the set increases the average “spread” of these numbers away from the mean. Therefore, the standard deviation of the new set must be greater than the standard deviation of the previous set. (Chapter 7, Lesson 1: Averages; Chapter 7, Lesson 2: Medians and Modes)
53. C
All the expressions may appear to simplify to 2x + y. However, when dividing, always remember that division by 0 is undefined. Can any of the denominators be 0? Yes: if x = 0 and y = 1, then the fraction in C equals 0/0, which is undefined, but all of the other expressions equal 1. The expression in C is equal to the other expressions except when x = 0. Therefore, the correct answer is C. (Chapter 6, Lesson 3: Simplifying Expressions)
54. B
The quadratic (Chapter 8, Lesson 4) on the left side of the equation can be factored with the basic factoring formulas (Chapter 6, Lesson 3):
x2 + 4x + 4 = (x + 2)(x + 2) = 0.
By the Zero Product Property (Chapter 8, Lesson 5), the only solution to this equation is x = −2, so the correct answer is B. (Chapter 6, Lesson 3: Simplifying Expressions; Chapter 8, Lesson 4: Analyzing and Factoring Quadratics; Chapter 8, Lesson 5: Solving Quadratic Equations)
55. B
Let’s call the positive number n. Decreasing the number by 10% is equivalent to multiplying it by 90%, or 0.90, so we can think of the question as which sequence of operations, when performed on n, yields 0.90n? The sequence in choice A yields n(1.20)(0.70) = 0.84n. The sequence in choice B yields n(0.10)(9) = 0.90n. The sequence in choice C yields (n/2)(1.40) = 0.70n. The sequence in choice D yields (n + 10)(0.8) = 0.80n + 8. Therefore, the correct answer is B. (Chapter 7, Lesson 7: Percentages; Chapter 7, Lesson 8: Percent Change)
Elite Questions for the SAT Math Test — Calculator
56. C.
Let’s define x as the original retail price of the laptop, in dollars. At 30% off, the discounted price is $0.70x:
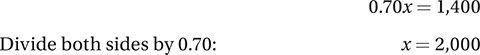
The final price including the additional discount is (0.85)(0.70)($2,000) = $1,190, so the difference is $2,000 − $1,190 = $810. (Chapter 7, Lesson 7: Percentages; Chapter 7, Lesson 8: Percent Change)
57. C
Your conversion should look like this:
Therefore, the correct answer is C. (Chapter 6, Lesson 4: Conversions)
58. B
Note that these equations are linear, and we only need two points to define a line. We are given two points: (0, 100) and (1000, 96.65), because BP must equal 100°C when x = 0 (at sea level), and BP must equal (100 − 3.35)°C = 96.65°C when x = 1,000. The equations in choices A, B, and D are all satisfied by the point (0, 100). However, only choice B is satisfied by (1000, 96.65).
Alternately, we can just calculate the slope from the two points: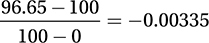 
, and see that only choice B is a linear equation with the correct slope. (Chapter 6, Lesson 5: Constructing and Interpreting Linear Equations)
59. C
The monthly streaming revenue can be calculated by multiplying the number of streaming customers by the monthly streaming fee that each customer pays. Let’s define r as the monthly streaming revenue before the change. If the monthly fee is increased by m% and the number of customers decreases by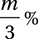 
, then the new revenue is 
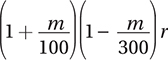, and the percent change is therefore 
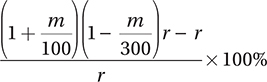, which simplifies to 
.
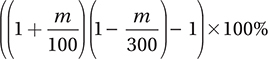and so the correct answer is C.
Alternatively, you can pick a convenient value for m that satisfies the conditions of the problem, calculate the percent increase from that, and compare this result to the answer choices. For instance, if you choose m = 6, then the percent change in revenue is 1 − (1.06)(0.98) = 0.0388 or 3.88%. Plugging m = 6 into the choices gives
A) −1.88%
B) −3.88%
C) 3.88%
D) 1.88%
So clearly only choice C matches. (Chapter 6, Lesson 1: Word Problems; Chapter 7, Lesson 7: Percentages; Chapter 7, Lesson 8: Percent Change)
60. B
Let’s graph what we know. We don’t know exactly where point B is, but it must be on the line x = −2. As the graph shows, there are two possible locations for B.
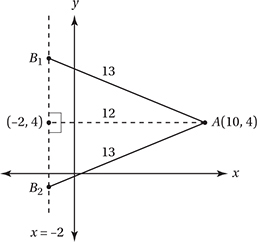
We can find the missing side of each right triangle with the Pythagorean Theorem, or just by noting that they are both 5-12-13 right triangles (52 + 122 = 132). Putting this information into the diagram shows us that B can therefore be at (−2, 9) or (−2, −1).
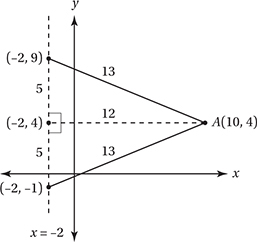
So the line we’re looking for contains (10, 4) and has a slope of either 5/12 or −5/12. Using the formula from Lesson 5, we can see that choice B has a slope of −5/12 and choice C has a slope of 5/12. However, only choice B is satisfied by the point (10, 4), so the correct answer is B. (Chapter 6, Lesson 7: Analyzing Linear Graphs; Chapter 9, Lesson 4: The Pythagorean Theorem)
61. A
This is essentially a conversion from gigabytes per month to minutes of gaming per day. Your conversion should look like this:
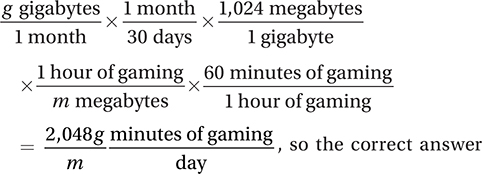
is A. (Chapter 6, Lesson 4: Conversions; Chapter 7, Lesson 5: Rate Problems)
62. C
The graphs of both equations are parabolas.
These equations show that the first parabola is “open down” with zeros at 2 and 8, and the second parabola is “open up” with zeros at 3 and 7. The average of both pairs of zeros is 5, so both parabolas have a line of symmetry at x = 5.
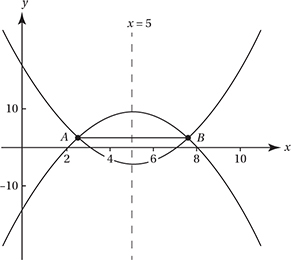
This means that the two points of intersection are also symmetric to the line x = 5, and therefore the length AB is just the absolute difference of their x-coordinates. If we combine the two equations by substitution, we can solve for these x-coordinates:
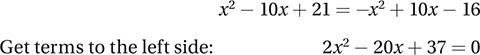
At this point, you could solve this quadratic and then subtract the two solutions, but as you can see by inspecting the Quadratic Formula, the difference between the two zeros of any quadratic in the form ax2 + bx + c = 0 is
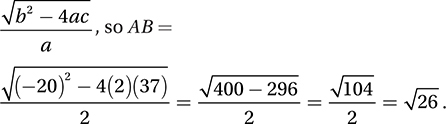
Notice that this value is slightly more than 5 but less than 6, which is confirmed nicely by our graph. (Chapter 8, Lesson 5: Solving Quadratic Equations; Chapter 8, Lesson 6: Analyzing Graphs of Quadratic Equations; Chapter 8, Lesson 8: Higher Order Systems)
63. D
Even though this is an inequality, let’s start with the corresponding equation |b + 3| = 2|b − 3|. The values of (b + 3) and (b − 3) are either the same sign or different signs. In other words, either (b + 3) = 2(b − 3) or (b + 3) = −2(b − 3). Let’s solve both of these: (b + 3) = 2(b − 3).
So b = 1 and b = 9 are the boundaries of the solution set. Now let’s test points in each of the three regions (b < 1, 1 < b < 9, and b > 9). Only values in the middle region (for instance, b = 3) satisfy the inequality, so the correct answer is D. (Chapter 6, Lesson 10: Graphing Inequalities)
64. A
The challenge here is to find equations that must be true about n, the number of components, and x, the pounds of carbon fiber left over. First, note that exactly A kilograms of aluminum is required to make n components, since no aluminum is left over. Since each component requires 70 kilograms of aluminum, 70n must equal exactly A. This equation is in both choice A and choice B, so we need to find another equation, this time involving x, the leftover pounds of carbon fiber. Since each component requires 25 kilograms of carbon fiber, n components require 25n kilograms of carbon fiber. Therefore the amount of carbon fiber left over must be x = C − 25n. If we add 25n to both sides of this equation we get C = x + 25n, and therefore the correct answer is A. (Chapter 6 Lesson 5: Constructing and Interpreting Linear Equations)
65.
y = 2/3 = 0.666 or 0.667 We could substitute for y in the first equation, but this would produce an annoying quadratic equation:
4(x + 4)(x + 1) = (x + 3)(x + 2)
But the question is asking for y, not x, so let’s be clever:
(Chapter 6, Lesson 12: Solving Systems with Algebra)
66. B
We don’t have enough information about the incomes of these athletes to calculate their average income or their median income precisely, but we do have enough information to do a basic comparison of their average and median incomes. Since there are 20 athletes, their median income must be the average of the 10th highest income and the 11th highest income, both of which must fall in the range of $250,000 to $750,000. Therefore, the greatest possible median income is $750,000.
We can also calculate the least possible average income by assuming that every athlete has the minimum income in her range. This gives us a lowest possible average of
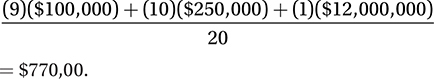
Since the least possible average income is greater than the greatest possible median income, the correct answer is B. (Chapter 7, Lesson 1: Averages; Chapter 7, Lesson 2: Medians and Modes)
BONUS: What do we call a data point like the $12,000,000 income in this set? What effect, generally, do such single large values have on the mean and median of the set?
67. B
For this one, we only need to know that standard deviation is a measure of “spread”: the more spread out the numbers are, on average, the larger the standard deviation. If we add 10 to each number in a set, for example, {2, 5, 8, 13} becomes {12, 15, 18, 23}, the set still has the same “spread”: each number is just as far from the mean as it was before. We can check: the average of the first set of numbers is (2 + 5 + 8 + 13)/4 = 7, and the average of the second set is (12 + 15 + 18 + 23)/4 = 17. So, in both sets, the “differences from the mean” are {−5, −2, 1, 6}. However, multiplying the numbers by 2 does change the spread. If we double all of the numbers in the first set, we get {4, 10, 16, 26}. The average of this set is (4 + 10 + 16 + 26)/4 = 14, and so the “set of differences to the mean” is {−10, −4, 2, 12}, which is double the previous spread. Therefore, the correct answer is B. (Chapter 7, Lesson 3: Data Spread)
68. A
But since k and m are arbitrary positive constants, km4 can be any positive number, such as 5. Therefore, the correct answer is A. (Chapter 7, Lesson 4: Direct and Inverse Variations)
69. B
Comparing the first two rows shows that doubling the concentration of A quadruples the rate of reaction. This means that the rate of reaction varies directly as the square of the concentration of A, and so the reaction is “second order in A.” This means that if we double the concentration of A again, as in the third trial, the rate of reaction should increase fourfold again, to 38.4. However, the rate of reaction in the third trial is half of that value: 19.2. This must be because the concentration of B was cut in half. Since cutting the concentration of B in half cuts the expected reaction rate in half, the reaction rate must vary directly as the concentration of B, and so it is “first order in B.” Therefore, the correct answer is B. (Chapter 7, Lesson 4: Direct and Inverse Variations; Chapter 7, Lesson 12: Analyzing Relations with Tables)
70. B
Let’s use m and v to represent the mass and volume, respectively, of asteroid B. This means that asteroid B has a kinetic energy of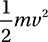 
. The problem tells us that asteroid A has a mass of 6m and a velocity of 
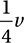, so it has a kinetic energy of 
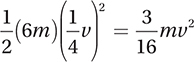. The ratio of these kinetic energies can be expressed as 
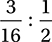, but we can simplify this ratio by multiplying both parts by 16 to get 3:8. (Chapter 7: Lesson 6: Ratios; Chapter 7, Lesson 7: Percentages; Chapter 7, Lesson 8: Percent Change)
71. C
If 5 kents is equivalent to 3 strones, then the conversion factor for converting strones to kents is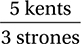 
and the conversion factor for converting kents to strones is 
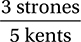. This means that 1 strone is equivalent to 
kent, and therefore 
.
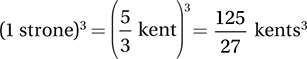(Chapter 6, Lesson 4: Conversions)
72. 48
Here’s a clever way to solve this problem. For a given distance, since 
, the time it takes to travel that distance is inversely proportional to the average speed (that is, the faster you go, the less time it takes). This means that if the ratio of her speeds is 45:30, the ratio of her times is 30:45, or 2:3. In other words, 2/5 of her total time is spent going to the interview and 3/5 of her total time is spent coming back from the interview. Since the total time of the trip is 120 minutes, it must have taken her (2/5)(120) = 48 minutes to get to the interview. (Chapter 7, Lesson 4: Direct and Inverse Variations; Chapter 7, Lesson 5: Rate Problems)
73. C
This problem is easy if you’ve memorized the translation key. If x is 0.06% of 1,000, then x = (0.06/100)(1,000) = 0.6. Therefore, 20% of x% of 1,000 is (20/100)(0.6/100)(1,000) = 1.2, so the correct answer is C. (Chapter 7, Lesson 7: Percentages)
74. 45
In the first 5 games, she made n shots out of 100, for an efficiency of n%. In the next 12 games, her efficiency increased to 1.20n%, so she made (0.012n)(200) = 2.4n shots out of 200. So, in the first 17 games, she made n + 2.4n = 3.4n shots out of 100 + 200 = 300 shots. If her shot efficiency for the first 17 games was 51%, she must have made (0.51)(300) = 153 shots altogether, so 3.4n = 153, and therefore n = 45. (Chapter 7, Lesson 5: Rate Problems; Chapter 7, Lesson 8: Percent Change)
75. C
A scaled image is similar (Chapter 9, Lesson 8) to its original image. If the corresponding lengths of similar figures have a ratio of a:b, then their areas have a ratio of a2:b2, and vice versa. The ratio of the areas is 3:192 = 1:64. Since the ratio of the lengths must be the square root of this ratio, the ratio of lengths is 1:8, so the diagonal of the new image is 8(3) = 24, and the correct answer is C. (Chapter 9, Lesson 8: Similarity)
76. A
Since quadratics and cubics have three or more parameters (the constants a, b, c, or d in the equations), any three points can be fit to one of these functions. However, the three points (1, 6), (2, 18), and (3, 54) are not collinear (check the slopes to confirm), so the correct answer is A. (Chapter 6, Lesson 5: Constructing and Interpreting Linear Equations; Chapter 8, Lesson 4: Analyzing and Factoring Quadratics; Chapter 8, Lesson 7: Higher Order Equations)
77. C
In the first 6 minutes, the population of Culture A increases from 200 to 1,400, which is an increase of 1,200, for an average rate of growth of 1,200/6 = 200 cells per minute. The population of Culture B increases from 400 to about 700, which is an increase of 300, for an average rate of growth of 300/6 = 50 cells per minute. Therefore, the population of Culture A increased 200/50 = 4 times faster over those 6 minutes, so the correct answer is C. (Chapter 7, Lesson 14: Nonlinear Relationships; Chapter 7, Lesson 15: Drawing Inferences from Graphs)
78. B
The rate of growth for Culture B is constant, so the divergence point must be when the rate of growth of Culture A is at a maximum. This is where the slope of its curve is steepest, which is somewhere between the 5-minute mark and the 6-minute mark. Therefore, the correct answer is B. (Chapter 7, Lesson 14: Nonlinear Relationships; Chapter 7, Lesson 15: Drawing Inferences from Graphs)
79. 33%
The total U.S. consumption of coal energy in 1990 was (0.27)(76.0 quadrillion) = 20.5 quadrillion BTU. In 2017, it was (0.14)(97.7 quadrillion) = 13.7 quadrillion BTU, which is a change of (13.7 − 20.5)/20.5 = −0.33, or a decline of 33%. (Chapter 7, Lesson 16: Pie Graphs)
80. D
According to the graph, from 1963 to 1993 the rate of violent crime per 100,000 capita increased from 150 to 750, and therefore increased at a rate of (750 − 150)/(1993 − 1963) = 20 crimes per 100,000 capita per year. If this rate of increase had continued for another 20 years beyond 1993, we would expect the incidence of violent crimes in 2013 to be (20)(20) = 400 greater per 100,000 capita than it was in 1993, or 750 + 400 = 1,150. However, the question is asking for the expected incidence per million capita, which is 10 times greater than the rate per 100,000 capita, or (1,150)(10) = 11,500 per million capita. (Chapter 7, Lesson 15: Drawing Inferences from Graphs)
81. C
Subtract 7 from both sides of the equation to express it in standard quadratic form: 6x2 + 4x − 7 = 0
Solve using the Quadratic Formula:
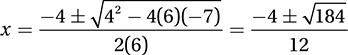
Since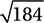 
is greater than 4, 
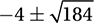will yield a positive real solution and a negative real solution, and so the correct answer is C. (Chapter 8, Lesson 5: Solving Quadratic Equations)
82. A
If f(g(x)) = x for all real values of x, then the functions f and g are inverses of each other, because performing them in succession on x just gets us back to x! If a function has an inverse, we can find it by just swapping x and y in its equation and solving for y.
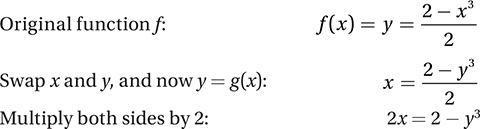
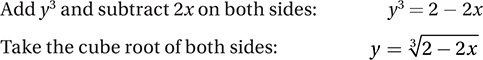
So the correct answer is A. (Chapter 8, Lesson 1: Functions; Chapter 8, Lesson 3: Compositions and Transformations)
83. C
Only choice C gives an x-intercept of 4, because shifting the graph down 5 units moves the point (4, 5) to (4, 0). (Chapter 8, Lesson 3: Compositions and Transformations)
84. 2.25
The graph contains the point (2.5, 2), so h(x) + 1 = 2.5, and so h(x) must equal 1.5. Therefore, x must be the input to h that gives an output of 1.5. According to the graph, this input is 2.25, because the graph contains the point (2.25, 1.5). (Chapter 8, Lesson 3: Compositions and Transformations)
85. 2
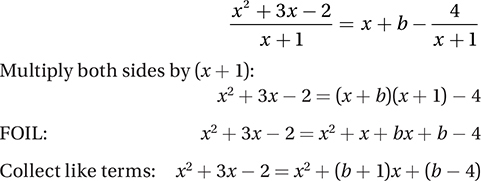
If the equation is true for all real values of x, then the coefficients must match and b + 1 = 3 and b − 4 = −2 must both be true, which they are only when b = 2. (Chapter 8, Lesson 12: Rational Expressions; Chapter 8, Lesson 13: Simplifying Rational Expressions)
86. C
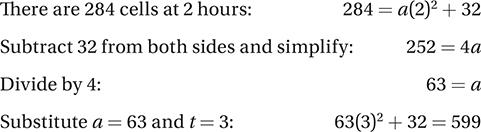
Therefore, the correct answer is C. (Chapter 8, Lesson 1: Functions; Chapter 8, Lesson 4: Analyzing and Factoring Quadratics)
87. B
One way to tackle this is to use the Quadratic Formula to find the solutions to the given quadratic, and then solve the equations in the choices and see which one has matching solutions.
However, it’s quicker to “complete the square.”
3x2 + 6x − 12 = 0
So the correct answer is B. (Chapter 8, Lesson 5: Solving Quadratic Equations)
88. B
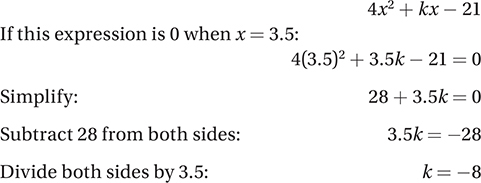
To find the minimum value we must find the y-coordinate of the vertex of y = 4x2 − 8x − 21. The axis of symmetry of this parabola is x = −b/2a = −(−8)/(8) = 1, so the x-coordinate of the vertex is 1 and the y-coordinate is 4(1)2 − 8(1) − 21 = −25. Therefore, the correct answer is B. (Chapter 8, Lesson 6: Analyzing Graphs of Quadratic Equations)
89. 5
By the Zero Product Property, if x + 4 is a factor, then x = −4 must be a zero of the expression. Substituting x = −4 into the expression and setting equal to 0 gives
Since this equation must be true for all values of y, k = 5. (Chapter 8, Lesson 5: Solving Quadratic Equations; Chapter 8, Lesson 7: Higher-Order Equations)
90. D
Although we can solve this system algebraically by substituting and solving a quadratic in x2, it is easier to draw a quick sketch to see that there are four solution points:
So the correct answer is D. (Chapter 8, Lesson 8: Higher-Order Systems; Chapter 9, Lesson 5: Circles)
91. 
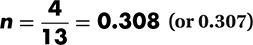
(Chapter 8, Lesson 8: The Laws of Exponentials; Chapter 8, Lesson 10: The Laws of Radicals)
92. 49
Just as an improper fraction like 
can be expressed as a mixed number,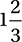 
, so an improper rational expression can be expressed as a “mixed” rational expression by long division. Let’s re-express the left side via long division:
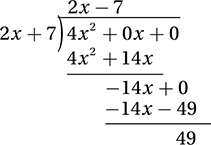
So, the correct answer is 49. (Chapter 8, Lesson 13: Simplifying Rational Expressions)
BONUS: We can also get the answer by substituting the zero of the denominator (x = −3.5) into the numerator: 4(−3.5)2 = 49.
93. B
We just need the percent change formula from Chapter 7, Lesson 8.
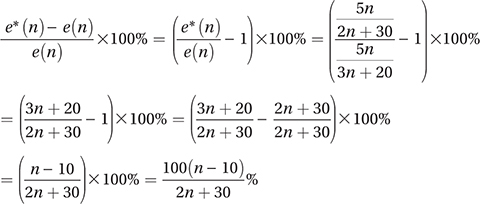
Therefore, the correct answer is B. (Chapter 7, Lesson 8: Percent Change)
94. A
Note the relationship that each angle has to the triangle in bold, and remember that the sum of angles inside a triangle is 180°:
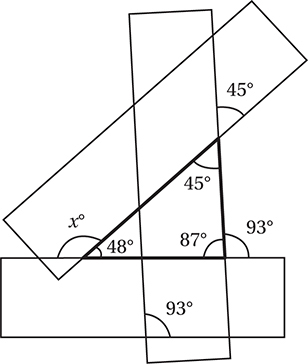
This shows that the x° angle is supplementary to the 48° angle, and so it must equal 180 − 48 = 132, and the correct answer is A. (Chapter 9, Lesson 1: Angles and Parallel Lines; Chapter 9, Lesson 2: Triangles)
95. B
Since h(9) = 0, the secant line must contain the point (9, 0). If we construct a line with slope −1 through (9, 0), we get a picture like this:
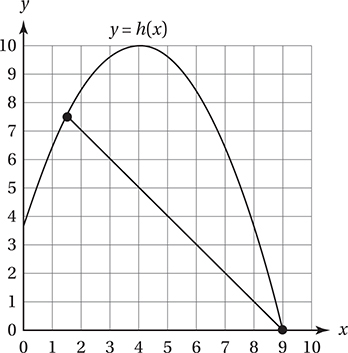
This shows that the y-coordinate of the other intersection point is somewhere between 1 and 2, so the correct answer is B. (Chapter 6, Lesson 5: Constructing and Interpreting Linear Equations)
96. B
To get this equation in standard circular form, we must complete the square, as we discussed in Chapter 8, Lesson 5.
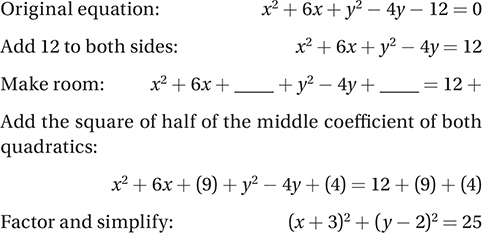
This is the equation of a circle with center (−3, 2) and a radius of 5. Therefore, its circumference is 2π(5) = 10π, and so the correct answer is B. (Chapter 8, Lesson 5: Solving Quadratic Equations; Chapter 9, Lesson 5: Circles)
97. B
Since the square has area 4, its sides must be length 2, so we can draw a triangle as shown:
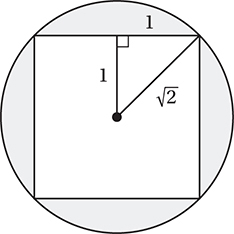
The shaded regions are just the area of the circle minus the area of the square, which is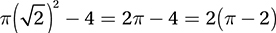 
, so the correct answer is B. (Chapter 9, Lesson 7: Areas and Volumes)
98. A.
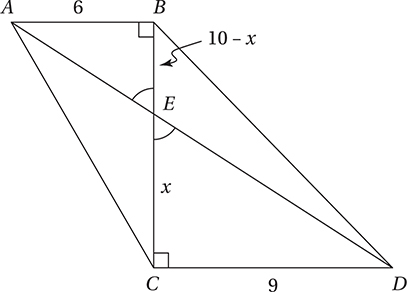
By the AA Theorem (Chapter 9, Lesson 8), triangles ABE and DCE are similar, and therefore their corresponding sides are proportional. Since BC = 10, if EC = x, then BE = 10 − x. Since these are corresponding sides of the triangles, 
, which gives us x = 6. Since triangle AEC has a base of EC and a height of AB, its area is (6)(6)/2 = 18, and so the correct answer is A. (Chapter 9, Lesson 7: Areas and Volumes; Chapter 9, Lesson 8: Similarity)
99. B
If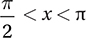 
< x < π, then x is in quadrant II:
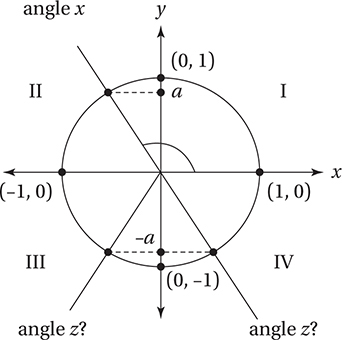
Since the sine of an angle corresponds to the y-coordinate of its point on the unit circle, angles with opposite sines correspond to points on the unit circle that are either reflections of each other over the x-axis or reflections of each through the origin. Since subtracting π radians (180°) from an angle is the same as reflecting it through the origin, the correct answer is B.
Alternatively, we can pick a value for x between π/2 (≈ 1.57) and π (≈ 3.14), such as x = 2. Since sin 2 ≈ 0.909 (remember to use radian mode on your calculator), we just need to find which angle among the choices has a sine of −0.909.
A) sin(π − 2) = 0.909
B) sin(2 − π) = −0.909
C) sin(2π + 2) = 0.909
D) sin(2 − π/2) = 0.416
So the correct answer is B. (Chapter 9, Lesson 9: Basic Trigonometry)
100. C
If in+1 = 1, then n + 1 is a multiple of 4, so n must be 1 less than a multiple of 4. We can just pick a number for n that is greater than 10 and that is 1 less than a multiple of 4, such as 20 − 1 = 19. This means that 6n = 6(19) = 114, which leaves a remainder of 2 when divided by 4 (because 114 = 28(4) + 2), and so the correct answer is C. (Chapter 9, Lesson 12: Imaginary and Complex Numbers)