2
THE CHANGELESS CHANGE
A new idea comes suddenly and in a rather intuitive way. That means it is not reached by conscious logical conclusions. But, thinking it through afterward, you can always discover the reasons which have led you unconsciously to your guess and you will find a logical way to justify it.
—ALBERT EINSTEIN
After many years spent developing my skills and ideas until they were good enough for publication in physics journals, I finally published my first independent paper in the Journal of High Energy Physics. My article made an iconoclastic claim: Einstein’s cherished idea of a constant speed of light could be violated in the early universe if our actual universe were a three-dimensional membrane orbiting a five-dimensional black hole. If this sounds like gobbledygook to you, in hindsight, it is. But twenty years ago, such subject matter was typical of what theorists worked on as they were trying to integrate cosmology and string theory. I was especially proud that the months of calculations I performed within the framework of string theory provided these new solutions.
And so there I was, excited to give my first professional talk at a picturesque university nestled in the mountains of Vancouver, Canada. They were my calculations I was going to talk about, so I knew them inside out, which contributed to my air of overconfidence. It didn’t last long. Within five minutes of my talk’s beginning, I was blasted with questions that soon transformed into a flood of criticism. Attempts to continue my talk ricocheted against random comments, delivered with a tone of unfriendliness, from the audience, attacking the premise of the talk: “Why should we believe our universe is a brane rotating around a 5D black hole?” I couldn’t help but feel unwelcome and alienated. By the middle of the talk I stood dejected, my fears of not being accepted as a peer erupting to the surface of my mind. Just because your paper gets published doesn’t mean that you will get into the club of physics. That day it felt obvious I hadn’t.
Then came a voice from the back of the room. The speaker was a distinguished Indian physicist in his seventies decked out in a well-groomed tweed suit. As soon as he began to speak, everyone shut up, as if a demigod commanded his minions to silence.
The old man stood up and said, “Let him finish! No one ever died from theorizing.”
It was the biggest lesson with the fewest words the audience and I could have learned about the art of theoretical physics. Those words would stay with me throughout my life as a theoretician. I took the old man’s admonition as a reminder to never be afraid of even the most absurd ideas, and to even embrace them. I finished my talk without further interruption and even got a round of applause afterward. Did I take my theory seriously years later? No, but the exercise of journeying into a theoretical territory and then journeying back has proven time and time again to be useful in surveying what’s possible and, hopefully, what describes and predicts the real universe. That moment was pivotal in my life and how I would engage the art of theoretical physics for the next twenty years.
A year after that talk, after many failed attempts, I landed a job as a postdoctoral researcher in theoretical physics at Imperial College in London. The department had been founded by Abdus Salam, who, along with Sheldon Glashow and Steven Weinberg, would win the Nobel Prize in Physics for discovering a unified theory of the weak nuclear interaction with electromagnetism. I was excited to be following in Salam’s footsteps along the road to becoming a research physicist. Yet somehow, despite my excitement, I quickly realized that road was not what I thought it would be.
At Imperial, weeks and then months of work could pass with little to show for it. If an idea did come to me, I invariably and quickly discovered that someone had already developed and published it. If I was performing a calculation, I would often hit a roadblock and have to learn new mathematical techniques in order to tackle it. By the time I learned the new math, someone would have already hit the finish line and published the result before me. These experiences forced me to wake up from my theory dreams to a reality in which the prospect of becoming a scientist seemed dim. My contract was for two years, but I relegated my expectations to another career, perhaps going on the road as a jazz musician or teaching high school physics, both admirable things to do. I would continue trying my best, but ideas simply weren’t coming, and I would continue to fake it and keep these frustrations to myself. I had everyone fooled.
Then one seemingly uneventful day, horror hit me. I received an email from our theory group administrator that simply said: “Professor Isham would like to speak with you.” I turned white like a ghost. Chris Isham was the head of our theory group and I feared that he had figured out that I was a fake. Everyone in our group revered Isham for his exceptional abilities in quantum gravity and mathematical physics. He was a tall Englishman with dark hair and piercing eyes and who walked with a slight limp. Like his friend and classmate Stephen Hawking, Isham suffered a rare neurological disorder that kept him in constant pain. I had kept away from him in fear of letting some gibberish slip out to ignite his physics bullshit detector. Now I suspected and feared that he had figured it out on his own, and my day had come to face him.
I decided to do a little preparation and read one of Isham’s papers. Perhaps I could appease him. To my dismay, many of his publications involved some of the most advanced concepts in math and physics, with inscrutable names such as topos theory, quantum logic, C-star algebras, and so on. I finally found a paper that he’d written two decades ago that I could grasp. It was about the behavior of quantum particles with half-integer spin, called fermions, in an expanding gravitational cosmology. Electrons, quarks, neutrinos, and most matter are examples of fermions, so it might seem a safe topic. Still, I set off nervously for the meeting.
I tensely walked into his large office filled with books, incomprehensible equations, and diagrams. On his desk an oddly placed small statue of an angel faced a visitor. After a brief hello, Isham didn’t waste time.
“Why are you here?”
I kept it real. “I want to be a good physicist.”
To my surprise, he said with a serious demeanor, “Then stop reading those physics books!” Then he pointed to an isolated bookshelf. “You see those books over there? They are the complete works of Carl Jung. Do you know that Wolfgang Pauli and Jung corresponded for decades? And Pauli’s dreams and analysis were key to his discovery of the quantum exclusion principle.”
Isham revealed that he had been studying Jung over the last fifteen years and had trained himself to do calculations in his dreams. I couldn’t believe that I was hearing this from one of the master mathematical physicists on the planet. Then he had a eureka smile and said, “You know what? How about you come to my office once a week? Write down your dreams and tell me about them.” He suggested that I read Jung’s Volume I, book 9 entitled Aion: Researches into the Phenomenology of Self as well as Atom and Archetype, a collection of two decades of letters between Jung and Pauli. At first, I was skeptical of the experiment. But I was also feeling isolated in the theory group, and Isham’s invitation to talk about my dreams was an opportunity to spend quality time with one of my physics idols.
Our weekly discussions started with me telling him about random dreams that had no apparent relation to physics, such as those about past relationships that continued to taunt me. During our time together, Isham would share his perspectives on some of the mysteries that our field faced. One of those was the problem of time in quantum gravity. While our physical (and psychological) experience of the flow of time is taken as fact, time disappears in the equations of quantum gravity. Isham worked on this problem and was a proponent of a new notion of time called internal time. It was no surprise to me to learn that these ideas were inspired by his exploration of psychology and mysticism.
As the weeks passed, I told Isham about what I thought was a trivial dream. In Jungian philosophy, dreams sometimes allow us to confront our shadows with the appearances of symbols called archetypes. I saw one here. I was suspended in outer space and an old, bearded man in a white robe—it wasn’t God—was silently and rapidly scribbling incomprehensible equations on a whiteboard. I admitted to the old man that I was too dumb to know what he was trying to show me. Then the board disappeared, and the old man made a spiraling motion with his right hand. Isham was captivated by this dream and asked, “What direction was he rotating his hands?” I was baffled as to why he was interested in this detail. But two years later, while I was a new postdoc at Stanford, I was working on one of the big mysteries in cosmology—the origin of matter in the universe—when the dream reappeared and provided the key insight to constructing a new mechanism based on the phenomenon of cosmic inflation, the rapid expansion of space in the early universe. The direction of rotation of the old man’s hand gave me the idea that the expansion of space during inflation would be related to a symmetry that resembled a corkscrew motion that elementary particles have called helicity. The resulting publication was key to earning me tenure and a national award from the American Physics Society. Chris Isham’s method proved to work for me. But he and I weren’t alone here. It turns out that some of the biggest breakthroughs in science were inspired by dreams, including Einstein’s theory of relativity.

Beginning when Einstein was a teenager hanging out in his father’s electric lighting company, he would play with imaginations about the nature of light. He would try to become one with a beam of light and wondered what he would see if he could catch up to a light wave. This matter found itself in the playground of Einstein’s subconscious and revealed a paradox in a dream. It is said that Einstein dreamt of himself overlooking a peaceful green meadow with cows grazing next to a straight fence. At the end of the fence was a sadistic farmer who occasionally pulled a switch that sent an electrical current down the fence. From Einstein’s birds-eye view he saw all the electrocuted cows simultaneously jump up. When Einstein confronted the devious farmer, there was a disagreement as to what happened. The farmer persisted that he saw the cows cascade in a wavelike motion. Einstein disagreed. Both went back and forth with no resolution. Einstein woke up from this dream with a paradox.
In the account of Einstein’s dream, and other accounts of the role of dreams in creative work, such as music, science, and visual art, there is a common theme: a paradox is revealed through imaginations that are contradictory in the awake state. It’s as if the mind’s eye can access an intuition beyond the waking state and not restrict our imaginations to the self-editing that our conditioning might impose during the waking state (unless you’re a great daydreamer). Perhaps dreams are an arena that can enable supracognitive powers to perform calculations and perceptions of reality that may be incomprehensible in our wake state. In my case, my paradox was making an equivalence between incomprehensible equations presented by the bearded man and his counterclockwise whirling hands. This counterclockwise motion turned out to summarize the mathematics that was obscuring the underlying physics to be unveiled.
My preoccupation with equations as the way to access deeper physical reality was confronted by this paradox. I discovered years later that I was not alone. My friend, virtual-reality pioneer, composer, multi-instrumentalist, and author Jaron Lanier told me that in his pre–virtual reality days, he used to hang out with Richard Feynman at Caltech. During that time Feynman was experimenting with other ways of doing physics, including using his body to intuit physics. This got the young Lanier thinking about how the human body could interact with computers in new ways and inspired what would become VR. Einstein’s paradox asks how it could be possible for both realities of light to be true. He ultimately resolved that paradox, and in doing so would uncover one of his most fundamental principles, one that was key in discovering not only his theories of special and general relativity but also the nature of all known four forces!
These thought experiments with light also led Einstein to other paradoxes, such as in James Clerk Maxwell’s theory of electromagnetism, which mathematically describes the motion of light waves. In this case, Einstein found inconsistencies that forbade absolute rest for a moving wave of light (an electromagnetic wave). In his groundbreaking 1905 paper On the Electrodynamics of Moving Bodies, Einstein resolves this inconsistency by elevating the role of principles in physical law. During Einstein’s time, physicists assumed that the universe is filled with a substance called the luminiferous ether that light could move through, like water waves moving through the medium of water. Mainly because of his intuition that an electromagnetic wave of light could never come to a complete stop, Einstein gave up the ether. Based on years wrestling with a handful of conundrums with electromagnetic theory, Einstein made an intuitive leap and postulated the principle of the invariance of light:
The Principle of Invariance of Light: The speed of light in empty space is the same for all inertial observers regardless of how fast they are moving relative to each other.
It’s worth saying a little about some of the physical reasoning that justified Einstein’s adoption of this principle. In his groundbreaking paper The Electrodynamics of Moving Bodies, Einstein finds a paradox in Maxwell’s equations that describe electric and magnetic fields. Both electric and magnetic fields exert forces on charged particles. It was well known since Galileo’s time that mechanical forces would be unchanged (invariant) for observers that are moving at constant speeds relative to each other. However, Einstein found that this was not the case for Maxwell’s equations. For example, different frames of reference would give different physical results for electric and magnetic forces. Einstein realized that this could be fixed if the electric and magnetic fields would also change into one another depending on the frame of reference.
Visible light is a manifestation of electromagnetic waves at a given set of frequencies that our eyes can detect. Einstein realized that if electric and magnetic waves traveled at a constant speed, the electric and magnetic force laws would remain intact. Einstein found that the transformations that related these moving observers, which are known as Lorentz transformations after the mathematician who first found them, did something surprising: they warped spatial and temporal measurements of relative observers. The consequence of Einstein’s insight is that we know electromagnetic waves are unified in four dimensions, three spatial and one temporal. And this relativity extended to all known laws.
Einstein realized that if time depended on the observer’s velocity it would be possible to retain the invariance of light in different moving frames. A similar argument was made for the length of objects in relative frames of reference. Therefore, both time and the sizes of objects are no longer absolute but are subject to change depending on how fast one is moving relative to another inertial frame of reference. The lesson here is that the invariance of the speed of light required time and space to be relative—we need relativity to have absolutes.
In our everyday experience, we simply do not experience time slowing down for us when we move faster. This is because the velocities we are used to are not large enough to see the relativity of time and space. Nevertheless, Einstein’s new theory made these bold predictions, and it was up to experimentalists to find a way to put them to the test. Not far from where I lived in Hanover, New Hampshire, when I was a member of Dartmouth’s physics department, the phenomenon of time dilation was finally confirmed by David Frisch and James Smith, who attacked the problem with the help of a particle called the muon. The muon is the cousin of the electron. Like the electron, a muon has a negative charge that we describe as −1, but there is a critical difference: a muon has two hundred times the electron’s mass. The muon is also unstable and will decay into an electron at a fixed rate of two-millionth of a second. Therefore, we can treat the decay of a muon as a standard clock. In 1941 Bruno Rossi and David Hall made use of the serendipitous fact that muons travel to Earth from outer space close to the speed of light to get a rough estimate of how moving at such a high speed dilates time. They measured the half-life of these rapid muons at high altitude and found, as Einstein had predicted, that these muons lived longer than muons that were at rest. In 1963 Frisch and Smith made much more rigorous measurements of the speed of extraterrestrial muons, which enabled an even more precise confirmation of how high speed warps time. These observations were refined and continued to be confirmed with the precise numerical predictions of Einstein’s theory of special relativity. But there is something even more special about special relativity.
Invariance isn’t just an empirical fact. The core idea behind invariance is based on the symmetry properties of geometric objects. The key insight in Einstein’s invariance principle is that physical entities like space-time and the other forces are in direct correspondence with geometry. It still baffles mathematical physicists why geometrical structures are linked with space-time and the building blocks of matter; no one has expressed this better than Nobel laureate Eugene Wigner, who wrote that “The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve.”
Consider the transformations of a square that leave it invariant. These are its symmetries. Rotate the square by ninety degrees and it looks the same. Rotate it again by ninety degrees and it still looks the same. Ultimately there are four successions of ninety-degree rotations that would leave the square looking the same. We can also flip the square about its horizontal center, and it looks the same. We can flip it about its vertical center and it also looks the same. We can flip the square across a diagonal line in two different ways and it looks the same. Therefore, there are eight different ways we can change the square and it looks the same. Said another way, there are eight transformations that leave the square invariant. The square is geometrically described as a two-dimensional object that has an eightfold symmetry. If I wanted to communicate with aliens that could not see, but knew numbers, I could describe many geometric objects by their symmetry transformations.
So, invariance captures an idea that science writer K. C. Cole describes as the differences that don’t make a difference. In the case of special relativity, I can move as fast or slow as I want, and the speed of light will not change. And this means that we can identify an underlying geometric symmetry. What would a world like that look like geometrically?
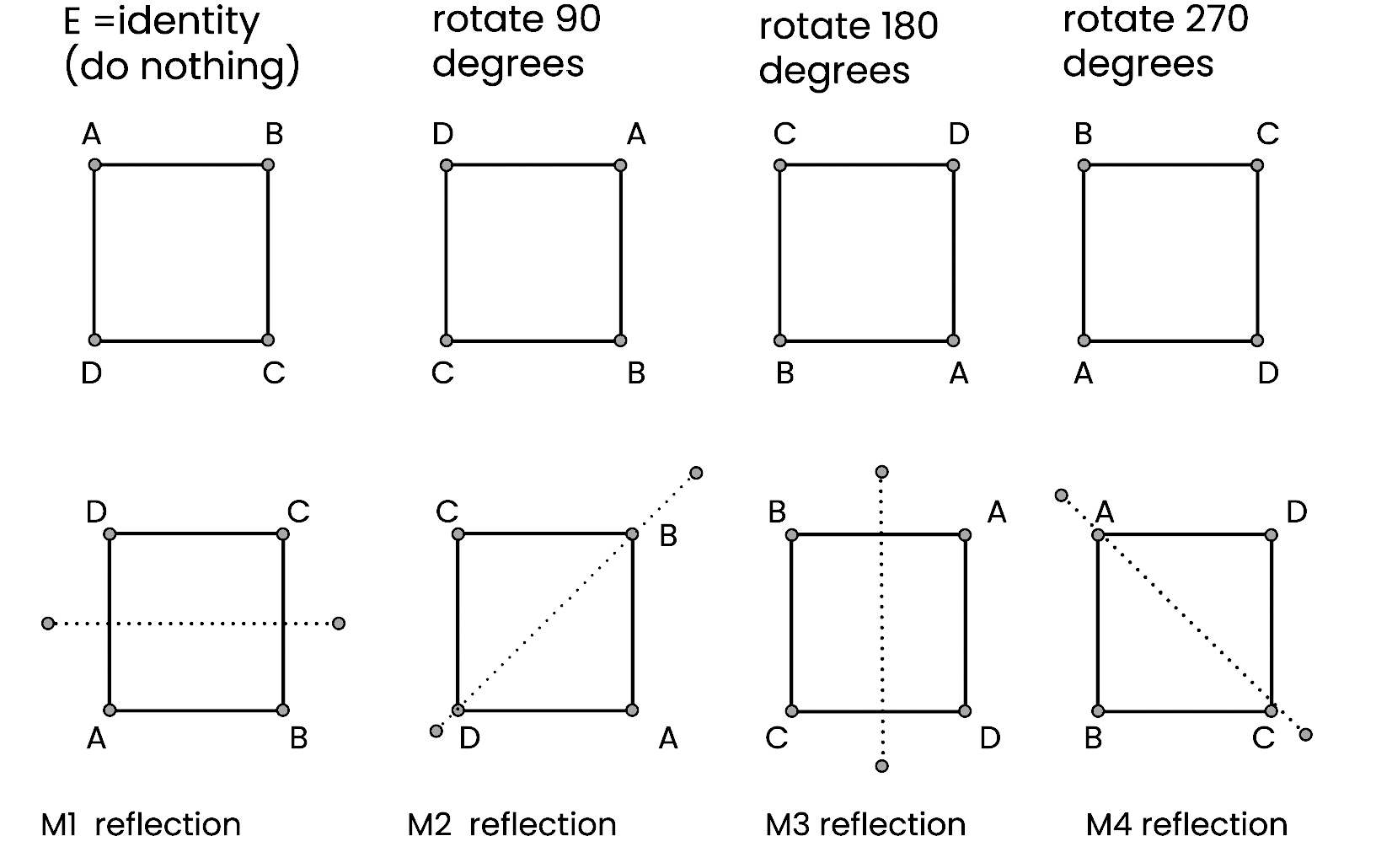
FIGURE 1: The eightfold symmetry transformations that leave the square invariant.
In special relativity Einstein found that there is a symmetry in all inertial coordinate systems that leaves the speed of light the same. The key to being able to enforce that the speed of light is the same in different inertial coordinate systems is to find the correct object, or observable, to relate coordinate systems to each other. The observables that we often use are distances and time. In three-dimensional space, distances alone are not sufficient because the position of a moving object can also have a direction. The mathematical object that describes distances with a direction is called a vector. Einstein realized that he could unite space and time into a four-dimensional vector, a space-time vector. This vector has a length and direction in both space and time. But to do this, we must put the time dimension on the same footing as a spatial dimension. The hack: multiply time by a velocity and we get a dimension of length.1 In this way the time dimension resembles a spatial dimension. Being equipped with a four-dimensional space-time vector enables us to relate them to each other in different coordinate systems. These relations or space-time vectors between different coordinates are exactly analogous to rotation transformations of points on a circle.
Consider an idealized Ferris wheel ride, where one person, Kolka, is on the Ferris wheel and another, Jim, is on the ground. Before the ride starts, both Kolka and Jim seem to share the same coordinate system, which they can label as points on an x-y plane. But as the Ferris wheel and Kolka start rotating, her coordinate system will be labeled by a rotating coordinate system. But even though both riders will disagree about their respective coordinates, they will agree on the invariant, which is the length of the radius of the Ferris wheel. In the same spirit, Einstein’s theory of invariance relates coordinates that differ from each other by relative velocities but retain their four-dimensional “radius” that remains unchanged by all observers. The compromise for preserving the four-dimensional radius is that observers that move at velocities comparable to the speed of light will experience the rate of time slowing down and lengths shrinking relative to observers that are at rest.
The four-dimensional space equipped for four-dimensional vectors was invented by Hermann Minkowski, who was inspired by his former student Einstein and realized that the system of relativity had an underlying geometry that is a four-dimensional space-time continuum that had a symmetry that left the speed of light as an invariant. The constant speed of light is formulated as the geometry of a cone embedded in a four-dimensional space. In this geometry a ray of light traces out the cone, and the slope of the cone represents the constant velocity. And just like the radius of a sphere remains the same length regardless of how one moves on the surface of the sphere, in this four-dimensional space-time the light cone would remain the same no matter what frame of reference is used.
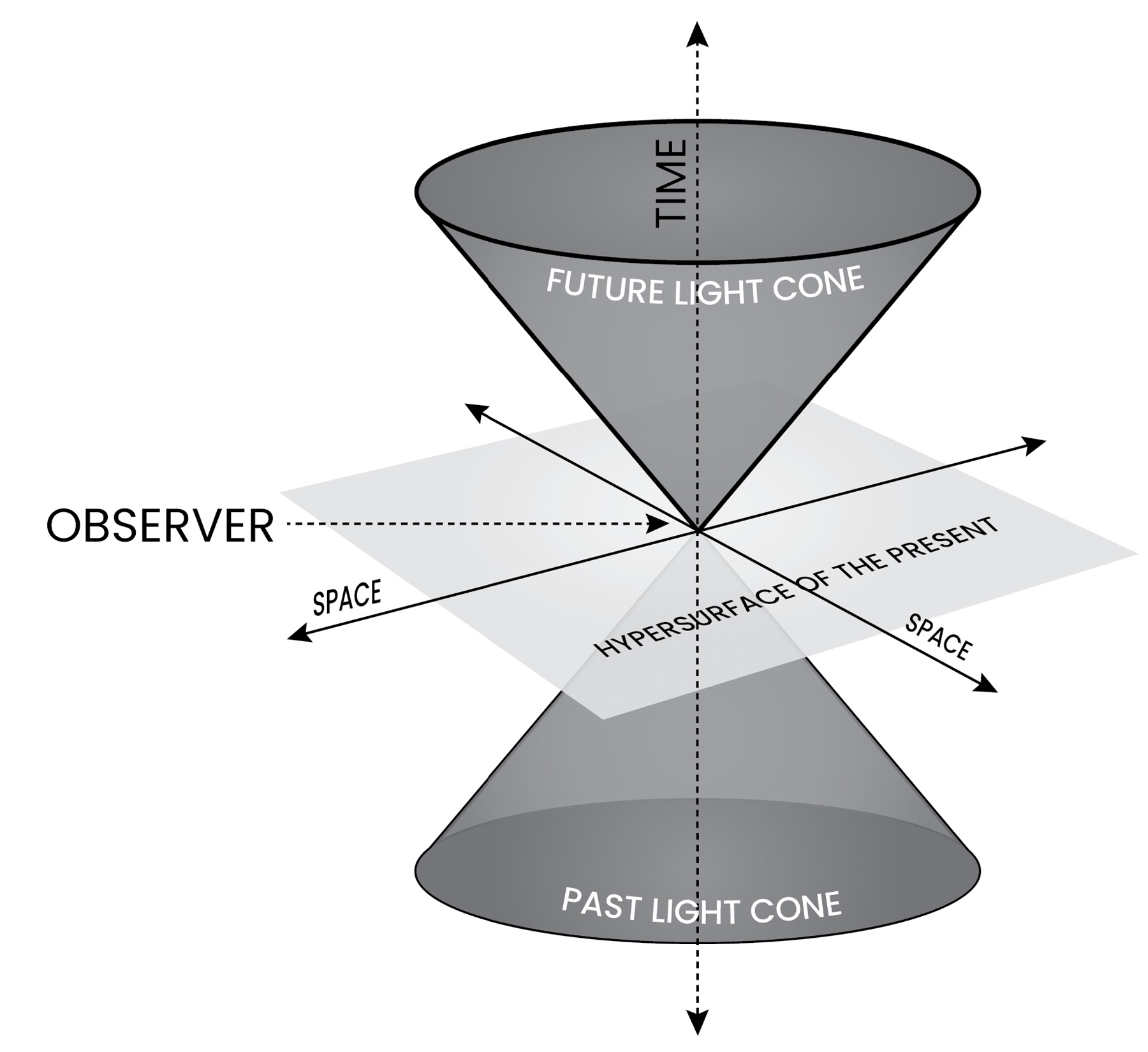
FIGURE 2: The light-cone structure of Minkowski space-time.
The triumph of special relativity was based on a simple and deep new principle of invariance, but the principle was so deep and universal that importance of the idea of invariance did not stop with special relativity. As we will soon see, the invariance principle became the master organizing principle behind all the physical forces, from all nuclear forces to gravity. Einstein further hypothesized that the laws of physics should not care about any relative state of motion, including those in which observers are accelerating relative to each other. If you are spinning in a rocket ship out in space or sitting still on a planet, the laws of physics will function identically. This led Einstein to perceive a reality beyond our five senses to discover a new law of gravity, the general theory of relativity, by deepening his invariance principle to observers undergoing any type of motion. He came to this realization by what he said was “the happiest thought of my life.”

General relativity is in hindsight a logical, but radical, step from its cousin, special relativity, which assumed the invariance of the laws of physics between observers that moved at constant speeds relative to each other: the jargon for this is that they are inertial observers. Those observers were all in reference to a fixed space-time structure, Minkowski space. But Einstein’s insight was to make the laws of gravity invariant for observers situated in wildly different space-time structures. This insisted that space-time can fold, warp, stretch, or generally be dynamical like an electric field. We are now ready for the master principle.
The General Principle of Invariance: All systems of reference are equivalent with respect to formulation of the fundamental laws of physics.
Einstein’s principle of invariance proved so powerful in the discovery and underpinning of special relativity that he used it to unearth the hidden reality of space-time and the gravitational force, which we know as the general theory of relativity, but it would also prove to be more influential again. As we will see, this turn of the tides, of placing symmetries as a central principle, would also become the driving force to writing down the other nuclear forces.
Einstein arrived at his theory of general relativity by a thought experiment—his happiest thought—by realizing that the experience of an accelerated person in the absence of a gravitational field (like a person inside a rocket ship accelerating in outer space) is the same as a person standing at rest on a planet with a gravitational field. The converse is also true. If you are in free fall in the presence of Earth’s gravitational field, your acceleration can “erase” the earth’s gravitational field. In other words, if a person is isolated in an elevator and is in free fall toward Earth, they would feel no gravitational forces.2 Einstein reasoned if acceleration could mimic the effect of a gravitational field, then gravity itself has to account for both acceleration and a gravitational field on the same footing. In other words, the law of gravity has to respect a symmetry between a constant gravitational field and accelerated motion without a gravitational field. How does one formulate such a symmetry? The strategy is to use what worked before, that is, special relativity.
General relativity requires invariance of the laws of physics regardless of the relative motion of observers. This requirement can be restated into a more general symmetry relating any type of coordinate transformation, called general covariance. For instance, a rotating observer will experience the laws of physics the same as a nonrotating observer.3 The compromise for putting all observers on the same footing gives two radical features of gravitation. The first is that the gravitational force is not a force in the way we’re used to thinking about it, but a feature of the curved space-time. In the Newtonian world an electric field could change the direction of a charged particle. In general relativity, particles will move in the straightest path possible. But in a curved surface, such as the surface of a sphere, the shortest distance between two points is not a straight line.
Imagine that you lived exactly at the equator of the earth and wanted to travel around the world using the shortest path to return home. The shortest path would be exactly a horizontal curve that circumscribes a great circle around the earth. This shortest path is not a straight line. Likewise, if space is curved then the shortest distance won’t necessarily be a straight line in flat space. These straightest paths are called geodesics, and what we call the gravitational force is simply a geodesic motion in a curved space that a star, for example, bends.4 The motion of Earth moving around the sun is nothing more than a geodesic due to the warping of space-time by the sun, and our planet is just moving around the contours of the curved space-time.
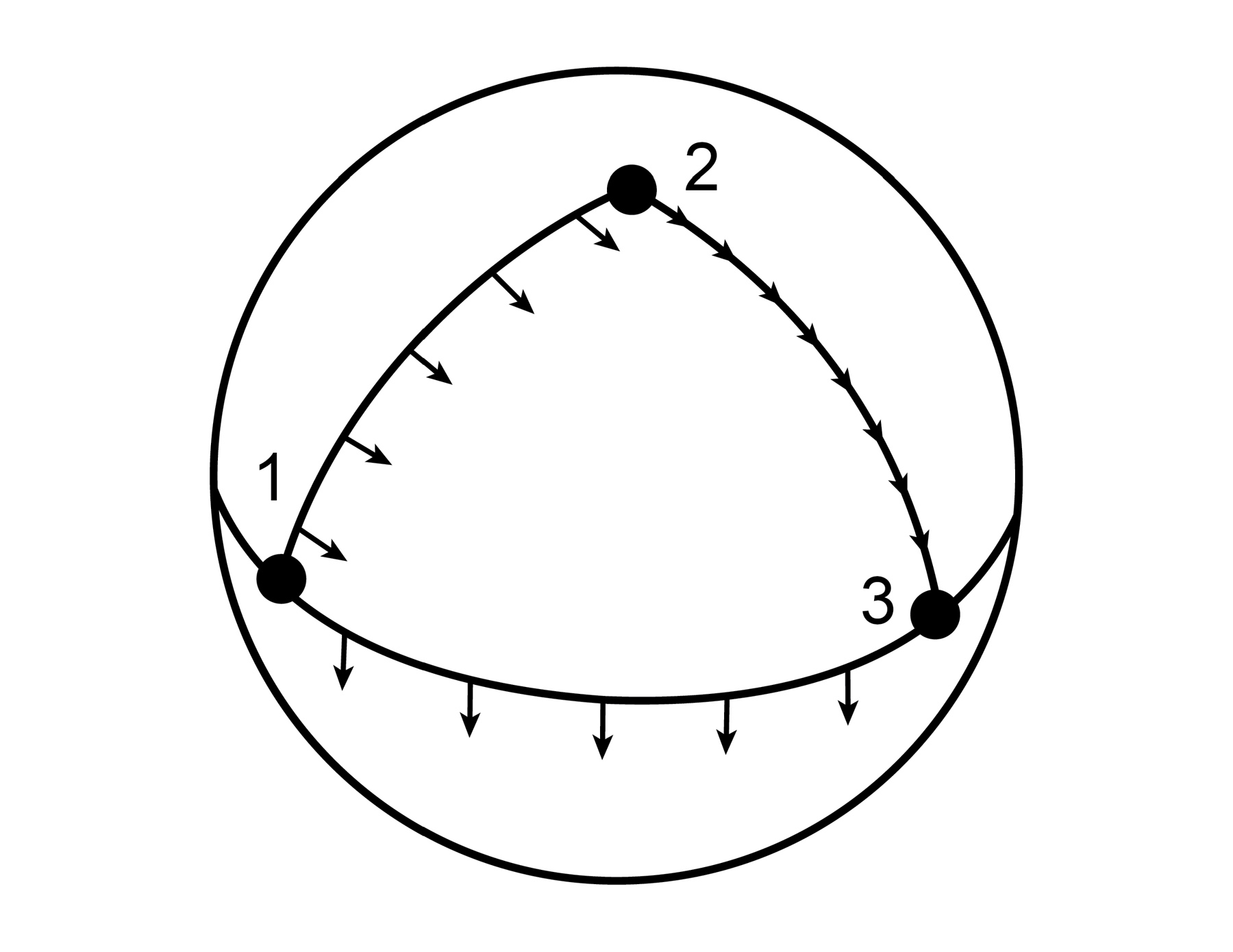
FIGURE 3: The intrinsic curvature on the surface of the sphere is measured by dragging and keeping parallel a flag around a closed circuit. The space is curved if the dragged flag fails to be aligned with its original orientation.
To do physics we need dynamical equations for the objects of relevance. For electromagnetism, the electric and magnetic fields obey a set of four equations codified by James Clerk Maxwell. The principle of invariance allows us to repackage all four equations into one equation that is invariant under the coordinate transformations of special relativity.5
I suffer from having a bad memory and always forget one of Maxwell’s four equations. So I was thrilled to realize that I can use the principle of invariance to write down one equation that contains all the other Maxwell equations.6 And using the same approach, Einstein figured out that there is an object that can codify the dynamics of space-time that respects the general coordinate transformations. Serendipitously this mathematical object was already discovered by mathematician Bernhard Riemann. The object, called the Riemann curvature tensor after its inventor, captures the dynamics of curved space-time in the presence of matter and energy. The famous Einstein equations of general relativity describe how the curvature of space-time is warped by matter and energy. And similar to the one Maxwell equation that contains others, the singular Einstein equation unpackages ten dynamical equations for the field of space-time.
Perhaps the most profound consequence of Einstein’s principle of invariance is that space-time itself is not some empty, fixed stage but rather is a dynamical field. But this leaves an interesting question. Since the gravitational field is space-time, when the gravitational field vanishes, does space-time itself cease to exist? In other words, what is no-space? We will revisit this question, but answering it will require that we meet our other principles first. Let’s jump into the quantum.

FIGURE 4: Three black holes affect the dynamics of space-time by warping the geometry of the space-time. This malleability of space-time has a range of physical effects including but not limited to gravitational forces and bending of light.