NOTES

Chapter 2: The Changeless Change

1. Mathematically we can define a space-time vector as 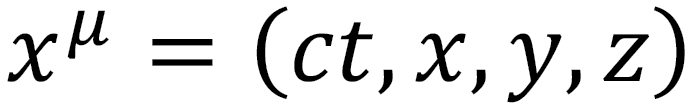where c is the speed of light and has dimensions 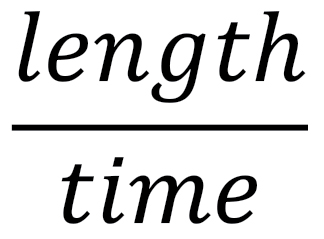. This gives the time axis a dimension of length since the dimensions of the time interval, 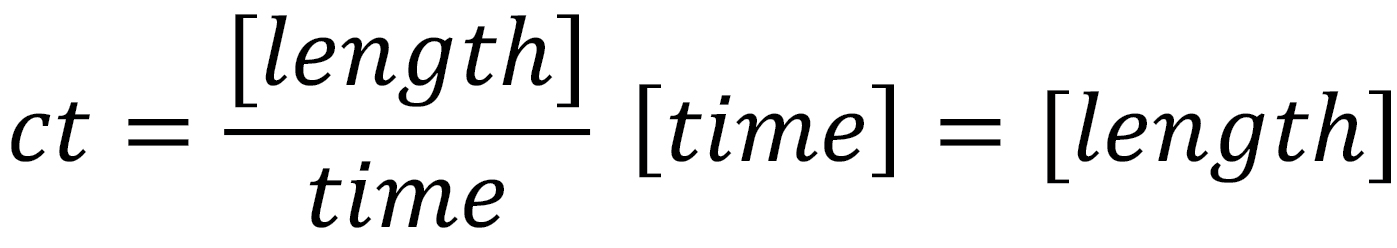, is length.

2. A local, freely falling observer in an exactly homogenous gravitational field experiences no forces. However, in a realistic situation there are gravitational field lines that are inhomogenous around the observer that will yield tidal forces.

3. Our direct experience of being in rotating environments seems different from being at rest, especially since rotation is a form of acceleration, which seems to mimic the effect of a force. We will soon see that this was part of Albert Einstein’s insight about the equivalence of acceleration and being subject to a gravitational field without accelerating.

4. A geodesic can be understood more geometrically with vectors that are tangent to a point on a curved space, called a tangent vector. If we take a tangent vector, 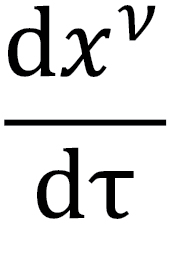, and transport it to a nearby region while keeping it parallel to itself, this amounts to satisfying the geodesic equation:

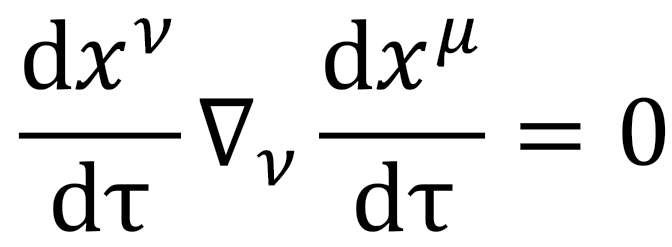
5. A solid example of a dynamical equation is that for how a pathogen like a virus grows in time:

Rate of growth of virus at a later time = (R-1)amount of virus at earlier time

Or symbolically

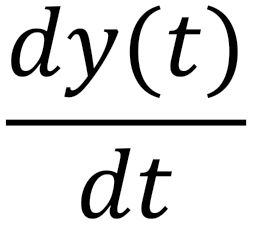 = (R-1)y(t)

Here R is famously known as the reproduction number. As I write this the COVID-19 virus has an average R of 2.3 in the United States. This leads to a solution of the number of infections to be exponentially growing in time .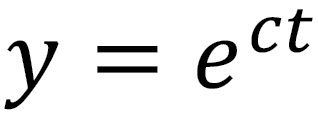

6. All four Maxwell equations are contained in one equation if we write it in a manifestly Lorentz covariant form: 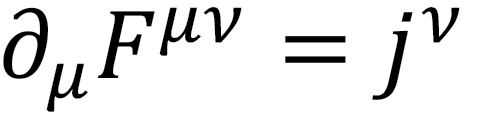. The left-hand side of the equation is the four-dimensional derivative of the field strength tensor that contains all electric and magnetic field information, and the right-hand side is the four-dimensional current, containing the electric charge and currents.

Chapter 3: Superposition

1. The concept of phase space was pioneered by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Phase space is a key tool in formulating thermodynamics and statistical mechanics and in identifying attractors in chaos theory.

2. The particles, like the photon, that communicate the forces between matter are called bosons and have integer spin. But half-integer spin belongs in Alice’s Wonderland. To get a feel, consider a child riding a merry-go-round. If the merry-go-round had half-integer spin, a child would have to go around two full rotations to ap-pear at his or her original position. Likewise, an electron needs to spin not 360 but 720 degrees to come back to its original spin orientation. M. C. Escher’s drawing of ants traversing a Möbius strip is an example of a space that requires two orbits to return to the same place. Another fundamental characteristic of an electron is that it never stops spinning.

3. I even used the concept of quantum entanglement in my role of science adviser for Disney’s A Wrinkle in Time, directed by Ava DuVernay.

4. Wave functions are vectors that live in a complex vector space called a Hilbert space. Said another way, a Hilbert space is a space of all possible wave functions and has all the usual properties of linear vector spaces commonplace to linear algebra.

Chapter 4: The Zen of Quantum Fields

1. Kensho is a Japanese word that translates to what Westerners call enlightenment, a liberating experience recorded by Siddhartha Gautama, the historical Buddha. According to the Buddha this potential to experience kensho is accessible to all humans. Similar accounts of the enlightenment experience were recorded by individuals across different cultures. Meister Eckhart calls it a breakthrough. The theologian St. Symeon calls it waking up. “I wasn’t there.” “There was only the tree.” “A sense of utter liberation and bliss.” “It is overwhelmingly positive.” “It’s like being drunk, but on reality.” “It’s more real than real.”

2. This cosmic ocean is called the vacuum state of quantum field theory. The vacuum state can both create and annihilate particles with quantum operators called creation and annihilation operators, respectively.

3. This “simple way” is a linear interaction between the photon vector potential and the fermion current. Such a linear interaction guarantees a local phase invariance for the electrons provided the gauge field simultaneously compensates the phase with its own phase transformation.

Chapter 5: Emergence

1. In modern times, solid-state physics is often called condensed-matter physics, which also involves the study of the various states of matter, such as liquid, gaseous, and crystalline, where many quantum particles interact quantum mechanically.

2. Kenneth Chang, “When Superconductivity Became Clear (to Some),” New York Times, January 8, 2008, https://www.nytimes.com/2008/01/08/science/08super.html.

Chapter 6: If Basquiat Were a Physicist

1. The electron can only have discrete (quantum) spin about its axis of rotation and never stops spinning. This is to be contrasted with a macroscopic spinning object, which can continuously change its spin orientation from up to down, such as when a top starts spinning and eventually falls to its surface. If the electron’s spin flips from up to down, it does so discretely, in a quantum unit of spin. And strangely, experiments seem to require one electron to coexist in a spin up and spin down state at the same time.

2. A conformal invariant theory is analogous to looking at features of a theory under a “magnifying glass.” This is equivalent to zooming in or rescaling the coordinates of the observables of the theory. If the predictions of the theory do not change under this zooming in, or zooming out, the theory is said to be scale-invariant. The microcosm has the same properties as the macrocosm. In some special cases, conformal invariance is the same as scale-invariance.

3. Thomas Kuhn, The Structure of Scientific Revolutions (Chicago: University of Chicago Press, 2012).

4. Du Bois wrote that “the Negro is a sort of seventh son, born with a veil, and gifted with second-sight in this American world,—a world which yields him no true self-consciousness, but only lets him see himself through the revelation of the other world. It is a peculiar sensation, this double-consciousness, this sense of always looking at one’s self through the eyes of others, of measuring one’s soul by the tape of a world that looks on in amused contempt and pity. One ever feels his twoness,—an American, a Negro; two souls, two thoughts, two unreconciled strivings; two warring ideals in one dark body, whose dogged strength alone keeps it from being torn asunder.” W. E. B. du Bois, The Souls of Black Folk (Orinda, CA: SeaWolf Press, 2020).

5. The conscience collective constitutes the shared social values within any social order; it regulates norms and activities in every social order, but it is not always well integrated; the values are not always consistent, and thus the social order might be poorly ordered. Here we might think about the conscience collective for both the larger society and for the community of physicists.

6. Phenomenologists sometimes call these cultural norms, which differentiate between sense and nonsense, the “lifeworld.” If the lifeworld is functioning effectively, it is tacit—we are unaware that we are seeing the world through it.

7. Durkheim recognized three functions of punishment. The first is the one usually discussed in the literature. Punishment creates an incentive to conform to social and cultural norms; it realigns what is in the interest of actors. Second, as noted in the text, punishment delineates the boundary of what is allowed. If a public violation of a normative expectation goes unpunished, it will undermine the clarity of the normative orientation; in contrast, the punishment of specific actions reinforces normative boundaries. Third is what we call the “sucker effect.” If conformity to a normative expectation continually disadvantages an actor, this will undermine her commitment to the relevant norm; she will feel like a sucker conforming while those who violate the norm are advantaged over her. If she knows, instead, that violators are likely to be punished for their violations, this enables her to sustain her sense of obligation.

8. There is a huge amount of sociological literature on deviance and marginality. Robert Ezra Park coined the term “marginal man,” but his usage was different than ours. Also relevant is Georg Simmel’s discussion of “the stranger.” Everett Hagen was one of the first to ask if deviance might be related to innovation. See his On the Theory of Social Change: How Economic Growth Begins (Homewood, IL: Dorsey Press, 1962), 573.

9. Eric Felisbret, “Legal Venues Celebrate Graffiti as an Art Form,” New York Times, July 18, 2014, https://www.nytimes.com/roomfordebate/2014/07/11/when-does-graffiti-become-art/legal-venues-celebrate-graffiti-as-an-art-form.

Chapter 7: What Banged?

1. The expanding universe model was independently discovered by

1. Alexander Friedmann et al., “Über die Krümmung des Raumes,” Zeitschrift für Physik A 10, no. 1 (1922): 377–86.

2. Georges Lemaître, “Expansion of the Universe, A Homogeneous Universe of Constant Mass and Increasing Radius Accounting for the Radial Velocity of Extra-Galactic Nebulæ,” Monthly Notices of the Royal Astronomical Society 91, no. 5 (March 1931): 483–90.

3. H. P. Robertson, “Kinematics and World Structure,” Astrophysical Journal 82 (November 1935): 284–301.

4. A. G. Walker, “On Milne’s Theory of World-Structure,” Proceedings of the London Mathematical Society, Series 2 42, no. 1 (1937): 90–127.

Chapter 8: A Dark Conductor of Quantum Galaxies

1. All observed galaxies have dark matter. See Jim Shelton, “New Studies Confirm Existence of Galaxies with Almost No Dark Matter,” YaleNews.com, March 29, 2019, https://news.yale.edu/2019/03/29/new-studies-confirm-existence-galaxies-almost-no-dark-matter.

2. The spatial anisotropy in the density of baryonic and dark matter deviates by approximately one part in ten thousand from the average homogeneous and isotropic cosmic microwave background thermal bath.

3. It was shown by Kris Pardo and David Spergel that it is difficult to reproduce the effects of dark matter in the CMB fluctuations in the early universe with MOND. See Kris Pardo and David Spergel, “What Is the Price of Abandoning Dark Matter? Cosmological Constraints on Alternative Gravity Theories,” Physical Review Letters 125 (October 19, 2020): https://arxiv.org/abs/2007.00555.

4. To be precise, dark matter is five times the density of baryonic (visible) matter.

5. Kaplan is known for producing the critically acclaimed film about the Large Hadron Collider, Particle Fever, which tells the story of the vision of the LHC and the physicists behind it. Coincidentally, I was the moderator for the world premier for the film at the NeueHouse in New York City.

6. Classical field theories have conserved quantities. For example, in electromagnetism the current is conserved. A quantized theory should also conserve all classical currents. However, there are some currents that are broken upon quantization. The amount of current that is broken is called an anomaly. However, a healthy quantum theory fixes these anomalies by realizing that topology needs to be considered in the quantum theory so as to reinstate the current conservation.

Chapter 10: Embracing Instabilities

1. The uncertainty principle can be conveniently written as 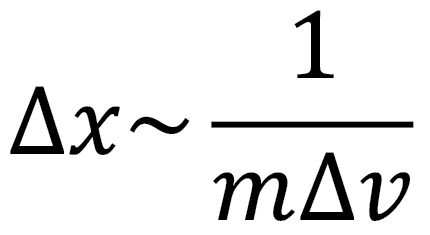, the uncertainty in the position of the particle in a harmonic oscillator is bounded by the size of the system. Therefore, the velocity can never be zero according to the uncertainty relation above.

2. General relativity provides an equation that relates energy and matter to the curvature of space-time. The configuration of the matter and energy should warp the space-time field in a specific dynamical manner dictated by the Einstein field equations similar to how a magnet emanates and bends a magnetic field surrounding it. Microscopically, a magnet emerges from interacting atomic spins in a metal. The cosmological constant interacts with the space-time in a manner that causes it to accelerate in its expansion without bound.

3. The Ashtekar variable is similar to QCD in that the dynamics of both theories are encoded in a gauge field connection. In QCD the connection enjoys a larger symmetry [SU(3)] than that Ashtekar connection, [SU(2)].

4. Stephon Alexander and Raúl-Rubio, “Topological Features of the Quantum Vacuum,” Physical Review D 101, no. 2 (2020); Stephon Alexander, Gabriel Herczeg, and Jinglong Liu, “Chiral Symmetry and the Cosmological Constant,” Physical Review D 102, no. 8 (2020).

Chapter 11: A Cosmologist’s View of a Quantum Elephant

1. I first spoke to Sir Roger Penrose, the inventor of twistor theory, who encouraged me to discuss the idea with Ashtekar. Twistors are maps from events in space-time to the celestial sphere that has close semblance to the symmetries enjoyed by the Ashtekar connection. I first thought that my idea behind parity violation and quantum gravity had to do with twistors.

Chapter 12: The Cosmic Biosphere

1. “John von Neumann Compares the Functions of Genes to Self-Reproducing Automata,” HistoryofInformation.com, http://www.historyofinformation.com/detail.php?id=682.

2. B. Jesse Shapiro et al., “Origins of Pandemic Vibrio cholerae from Environmental Gene Pools,” Nature Microbiology 2, article no. 16240 (2017).

As Salvador Almagro-Moreno communicated to me, “Virulence adaptive polymorphisms (VAPs) circulate in environmental populations and must be present in the genomic background of a bacterium before it can emerge as a successful pandemic clone.”

3. The entropy of a black hole is calculated to be .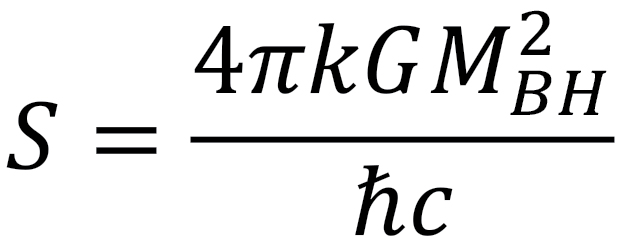

4. Ludwig Boltzmann, “The Second Law of Thermodynamics,” in Theoretical Physics and Philosophical Problems, ed. B. F. McGuiness (New York: D. Reidel, 1974).

5. One potential loophole to the low-entropy initial state is that there was a previous state what was actually even more entropic that reduced its entropy. For example, if the big bang started out dominated with black holes, then they could evaporate and produce the CMB radiation. If the massless radiation, such as photons, got homogeneously distributed then decayed into matter, then we would have a lower-entropy situation. However, the original entropy presumably in the form of black holes would have to get diluted. This idea can perhaps be implemented in a mechanism developed by Peter Mészáros and me where we postulated that primordial black holes that form after inflation could explain the CMB and dark matter if they undergo Hawking evaporation.

6. Fred C. Adams et al., “Constraints on Vacuum Energy from Structure Formation and Nucleosynthesis,” JCAP 03 (2017).

Chapter 13: Dark Ideas on Alien Life

1. A similar phenomenon happens with electrons and magnetic fields in the fractional quantum Hall effect.

Chapter 14: Into the Cosmic Matrix

1. Arvind Borde and Alexander Vilenkin demonstrated that even cosmic inflation is geodesically incomplete and does not escape the cosmic singularity. See Arvind Borde, Alan H. Guth, and Alexander Vilenkin, “Inflationary Spacetimes Are Incomplete in Past Directions,” Physical Review Letters 90, no. 15 (April 15, 2003).

2. To be precise, if x and p are position and momenta variables then quantization rules promote their Poisson brackets (curly brackets) to commutation (square brackets) 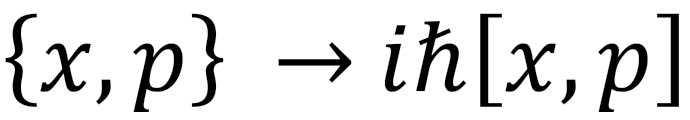. Classical dynamics of an observable is given by Hamilton’s equation, which states that the time evolution is generated by the Poisson brackets of the Hamiltonian and the observable of interest. For example, the classical time evolution of the position of a particle, x(t) is given by the Poisson bracket between the Hamiltonian and the position.

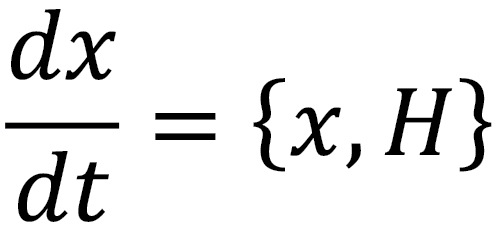
Whereas the time evolution of the position operator is given by the commutator between the Hamiltonian and position operators.

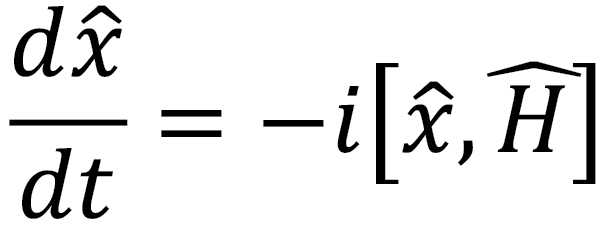
3. Here we are assuming that the spatial dimensions have the topology of circles whose local products are tori. These topologies admit one-cycles that strings can wind around without collapsing to a point.

4. This initial condition for string cosmology is an extension of the Copernican principle in the standard big bang, which states that there is no preferred vantage point in the universe. The Copernican principle is consistent with assuming homogeneity and isotropy not only in space but in the degrees of freedom that occupy the universe.

5. A cyclic BV mechanism was studied by Brian Greene, Daniel Kabat, and Stefanos Marnerides. They found that the BV mechanism can exhibit a cyclic cosmology if the theory incorporates higher derivative terms in the gravitational theory.

6. In a closed string theory we can add open strings that satisfy both von Neumann and Dirichlet boundary conditions.

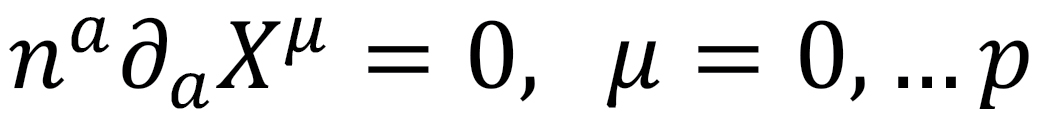
The above equation states that the derivate of the string ends on p space-time dimensions. This is a Dirichlet boundary condition. This p-dimensional hypersurface defines the worldvolume of a Dp-brane.

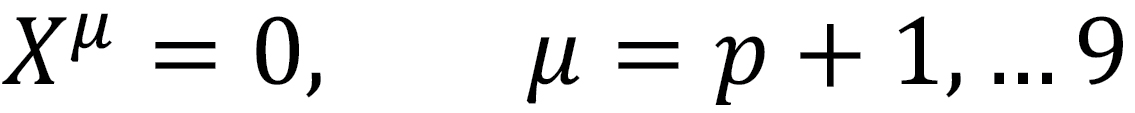
7. The above equation states that the string vanishes in the other dimensions.

Chapter 15: The Cosmic Mind and Quantum Cosmology

1. Deepak Chopra, MD, and Menas C. Kafatos, PhD, You Are the Universe: Discovering Your Cosmic Self and Why It Matters (New York: Harmony Books, 2017).

2. Kimbwandende Kia Bunseki Fu-Kiau, African Cosmology of the Bantu-Kongo: Principles of Life and Living (Brooklyn, NY: Athelia Henrieta Press, 2001), 17–54.

3. In general relativity the Hamiltonian is constrained to be zero. As a result the associated Schrödinger equation will no longer have time dependence. The state of the universe will therefore be timeless, which means that the universe as a whole is changeless. In order to obtain time dependence, one has to introduce an external clock relative to the rest of the universe, and matters of this sort are called the problem of time in quantum gravity.

4. Alexander Vilenkin, “Creation of Universes from Nothing,” Physics Letters B 117, no. 1–2 (November 1982): 25–28.

5. Andrei Linde, “Universe, Life, Consciousness,” https://static1.squarespace.com/static/54d103efe4b0f90e6ca101cd/t/54f9cb08e4b0a50e0977f4d8/1425656584247/universe-life-consciousness.pdf.

6. Vincent Jacques et al., “Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment,” Science 315, no. 5814 (February 16, 2007): 966–968, https://arxiv.org/abs/quant-ph/0610241.