8
A DARK CONDUCTOR OF QUANTUM GALAXIES
The energy in the undulations that grew under gravitational collapse some fourteen billion years ago needed an invisible form of matter to efficiently form the billions of galaxies including our own Milky Way.
We can measure the effects of dark matter in different ways. The rotation of stars in galaxies is the most direct. Today we see the striking presence of dark matter in all galaxies, which is inferred from an anomalous rotation.1 How is this? When we look at gravity at distances comparable to our galaxy, it fails to account for the motion of our sun and solar system around the Milky Way. The speed of a star like our sun around our galaxy is proportional to the amount of mass it contains. From this, we can infer from the sun’s velocity that about 85 percent of the mass is missing or invisible/dark. In other words, our sun is moving so fast that if there weren’t some hidden form of matter providing the necessary gravitational pull, it would fling off from the Milky Way into oblivion. We have even found that every galaxy is made up mostly of dark matter.
A second way we can measure the effects of dark matter is through a phenomenon called gravitational lensing. Similar to the bent lens of a magnifying glass, a gravitational lens is a region of warped space that causes light that traverses it to get distorted. Imagine that there is a massive blob of dark matter in front of a galaxy. Although we will be able to see a visible galaxy that lurks behind the dark blob, the image of the visible galaxy will appear to be distorted in a definite way according to general relativity. We can infer the mass of the dark blob from the lensed image of the visible galaxy.
So, we now know from observations that dark matter exists in individual rotating galaxies and clusters of galaxies that form a cosmic web of interconnected galaxies spanning cosmic distances. I fooled a neuroscientist who thought that a picture of this structure looked like how the brain is wired with neurons. There is invisible dark stuff that pervades the universe, and aside from being the cosmic glue that keeps stars like our sun in orbit, invisible things have a way of being taken for granted. So why are physicists and astronomers so interested in dark matter? We believe that unveiling dark matter is a puzzle piece that will help us understand the fundamental nature of our physical world. And we suspect that once we crack the dark matter code, we will come to know something unanticipated. After all, did Einstein ever imagine that the quantum nature of the photon would lead to solar cells? Ever since its discovery, we have been cooking up theories to account for dark matter, and despite our efforts, we have not been able to identify the one true model behind its mystery. We are not short of imagination, as there are hundreds of candidates for the identity of dark matter. Let’s say that you wanted to construct your dark matter model. There are some necessary criteria that it needs to satisfy.
Our standard big bang cosmology suggests that dark matter may have been born in the very early universe at least fourteen billion years ago along with the visible matter, and based on the observation of the cosmic microwave background radiation, both dark and visible matter were distributed across the universe soon after their creation. After the dark matter is created, it must remain stable throughout cosmic history, meaning that it cannot annihilate or decay so that it can cluster to form the scaffolding for the visible matter to form stars and galaxies. Second, for the dark matter to do its job to aid gravity in sculpting the cosmic structure, it must be cold, or equivalently, the dark particles must be motionless, which endows dark matter with the properties of a pressureless, frictionless fluid. The opposite of this is a gas of particles bouncing around so fast that their high momentum would make them hot, which would not allow structure to form.

FIGURE 14: An artist’s impression of the three-dimensional map of the network of large-scale distribution of dark matter in the universe. Apparent in the map are filaments of dark matter that continue to collapse under gravity to seed galaxies.
As a result, the pressureless dark matter fluid does not exert any preferential flow in any direction, so it would rather stay put—much like an invisible cosmic Silly Putty. The dark matter fluid, during the earliest stages of cosmic structure formation, does undergo localized undulations, creating distortions of attractive gravitational energy in the fluid. A correct understanding of the origin of these undulations of the dark matter is still a matter of research and will be discussed in the chapter on the physics of the very early universe. The energy in overdense regions of dark matter generates a gravitational attraction to enhance its gravitational pull on the nearby visible matter that was around in the early universe, such as electrons and photons. The visible matter will collapse around the center of the location of dark matter density, eventually forming the region for a protogalaxy. The process I just described is more complicated since it is quantitively described by a set of coupled differential equations describing how dark matter sources gravity, and how the visible matter exerts radiation pressure to create oscillations as it collapses.2 The system quickly becomes nonlinear and requires numerical physics to analyze thoroughly. But the takeaway is that once we specify the dark matter, visible matter, and general relativity, we get the correct predictions for the imprint of this physics in the observed temperature fluctuations in cosmic microwave background radiation.
So how do we make progress given the limited things we know about dark matter and the plethora of theoretical models on the market? Most models fall into two categories. One is that dark matter is simply a new particle that’s not found in the pattern of fields in our standard model. This dark particle/field will just interact very weakly with the visible matter. Recall that these patterns follow from symmetries that relate these fields to each other. The other theme for dark matter is that there is no dark matter, but the force of gravity changes in the contexts where we see the effects of dark matter. We call these models modified Newtonian dynamics, or MOND, a hypothesis created by the physicist Mordehai Milgrom.
The basic idea of MOND is that Newtonian gravity is valid on solar system scales. Still, as we go into the regime of galaxies, gravity gets modified to account for the observational fact that all spiral galaxies rotate at a universal acceleration that is proportional to the expansion rate of the universe. Galaxies are gravitationally bound and isolated systems that are decoupled from the expansion rate of the universe. A typical galaxy is on the order of one thousand parsecs, and a cosmic expansion occurs at distances around billions of parsecs. So how could galactic rotation communicate with the universe’s expansion rate? The jury is still out, but the scientific community leans toward dark matter being a new particle due to the observation of the bullet cluster—two galaxies that collided with each other—leaving in its wake a separation of dark matter and the visible matter of the two galaxies. This observation is tough (but not proven to be impossible) to be explained with MOND.3

During most of my college and graduate school years, I was a competitive 800-meter runner. I trained religiously for three hours five days a week to meet my goal of finishing the half-mile in one minute and 51 seconds. Over the years, I would coincidentally see the number 151 appear when I looked at the time, the number on a billboard, and many random places.
The number 151 seemed to appear at a frequency greater than any other number. I took this coincidence as an indication that one day I was bound to run that time, but twenty years have gone by and I still haven’t. These days my knees would not even get me through four hundred meters in two minutes. Had I not given so much significance to the coincidence of the number 151, I would have settled my goals on a more realistic 154 for the 800. But aside from sports and gambling, the seduction of coincidences also creeps up in physics.
One of the themes in attempting to solve a problem in theoretical physics appears in coincidences. In the dark matter world, a few coincidences are floating around. When we try to make progress using a coincidence, it’s crucial to be mindful of our tastes and prejudices. One of the most popular coincidences led to the possibility that dark matter could be detected directly from its interaction with matter subject to a weak nuclear interaction. The early universe is a hot thermal soup of particle species. If dark particles exist and interact, then they will also exist as a thermal soup as well because the density increases in the past universe. Most particles, including dark particles, come with their associated antiparticle that can annihilate into lighter and more stable particles like electrons and photons. Still, this process is suppressed as the universe cools and expands, since it is less likely for particles to find their antiparticles as they run away along with the expanding universe. There is a beautiful relationship between how the decay of a heavy particle into a light one will depend on the mass and energy, and this applies the same way for both dark and visible matter.

FIGURE 15: A schematic representation of the dark matter halo surrounding the Milky Way, with a supermassive black hole at the center.
What is the lightest mass and interaction strength necessary so that the decaying soup of heavy, dark particles can give the correct density of dark particles in the universe today? It turns out that the mass of the dark particle is related to that of the weak interaction of visible matter. This is a numerical coincidence and is famously called the WIMP (weakly interacting massive particle) miracle.
There is another good reason astrophysicists took the WIMP miracle seriously. One of the great successes of the standard model of particle physics is the Higgs mechanism, which endows mass to all the particles known to us. The Higgs field accomplishes this feat by breaking the symmetry associated with the weak interaction at the energy scale commensurate with the Higgs particle. A big reason for building the Large Hadron Collider was to search for new anticipated particles at the mass scale of the Higgs mass, which would give insight into the nature of electroweak symmetry breaking and the physics beyond the standard model.
WIMPs have created excitement because of their prospect for being directly detectable in particle colliders and other creative forms of direct detection here on Earth. For example, every once in a while, a WIMP can travel to Earth from a galactic halo and interact weakly with an atomic nucleus, which could give a detectable signal according to the specific type of WIMP particle and its interaction with the nucleus. My colleague Rick Gaitskell at Brown has been one of the pioneers of the quest to detect WIMPs and other dark particles directly. It’s been about forty years, but so far, and with ingenious and laser-sharp accuracy in detecting the faintest interaction with WIMPs, there has been no direct detection. These direct-detection experiments have allowed us to highly constrain and rule out a large class of WIMP models. Still, a number of models, predicting a variety of possible particles to fill the role of WIMPs, survive, and the hunt is still on to see which of those particles might actually exist. There are some interesting anomalies among the different experiments that suggest that WIMPs may be the culprit. I remember having lunch not too long ago with one of the co-inventors of the WIMP miracle model. She lamented to another dark matter theorist, “It’s been over thirty years; where are the damn WIMPs?” So, let’s assume that the dark matter is not a WIMP. Then what are we left with? For one thing, if it is not a particle, then what else could be in the sky?

One uneventful fall day after teaching my general relativity course, I noticed an email from my colleague David Spergel, a pioneering cosmologist, director of the Simons Center for Computational Astrophysics, and now president of the Simons Foundation. He said that he would be passing through Providence and would have a free half-hour to meet. Spergel was one of the first people to notice the WIMP miracle while he was a young graduate student and later with renowned cosmologist Katie Freese figured out an ingenious way to detect WIMPs. We decided to have a quick dinner close to the Amtrak station in downtown Providence.
I knew that Spergel was a tad frustrated that WIMPs had not been detected after decades of relentless searches, and I saw this as an opportunity to pursue viable alternatives with him. Over a course of Malaysian food, we wasted no time, and I asked him: Aside from the WIMP miracle, what was the most pressing observational mystery behind dark matter that needed to be addressed?
He reminded me of another coincidence, an observation that he was among the first to notice. The observed density of dark matter is the same magnitude as the visible matter density—and a fundamental explanation was lacking.4 This coincidence is even more striking because visible and dark matter don’t seem to interact with each other.
After going back and forth, we realized that the link between dark and visible matter could be addressed by their common origin in the early universe. The realization was fueled by the need to combine the quantum principle with the gravitational side of dark matter. As we will soon see, not only does dark matter gravitate but gravity plays a key role in the origin of dark matter, and this would have problems without quantum mechanics. A part of this issue was pursued and addressed by particle physicist David Kaplan in the 1980s.5
Kaplan is known to be one of the most creative particle physicists in his generation, and his idea called asymmetric dark matter was the first to connect creation of matter over antimatter to the creation of dark matter, attempting to explain the coincidence between their densities in the universe. But, how could it be that dark and visible matter can have a joint creation without ever “knowing” about each other? Plus, it is not enough to provide a candidate for dark matter that solely explains its properties in the current universe. It is useful to understand baryogenesis itself to answer the potential link behind dark and visible matter. Even if we were to understand the origin of the dark matter, David Spergel and I understood that our model was calling for something that was not a WIMP. It is first useful to understand how dark matter can be cocreated with the visible matter, otherwise known as baryogenesis—the origin of baryonic matter, such as protons and neutrons.
As it stands, there is no consensus among cosmologists about the creation of matter over antimatter in the universe. But there are some conditions that most of us agree on, which have to do with the known symmetries of the vacuum state of the quantum fields that give rise to all the matter and antimatter. The critical insight into baryogenesis is that special symmetries that related matter to antimatter had to be desecrated by new physics that operated in the very early universe. And as we will see, these symmetries are not cherished in our universe. In 1967 the Russian physicist Andrei Sakharov provided the necessary ingredients to accomplish baryogenesis—these were famously known as the Sakharov conditions. These conditions fit into the principle of emergence that I discussed earlier, where we see that the violation of invariance leads to a variety of complex, emergent, and physical properties. Baryogenesis transpires to be a most crucial cosmic example of the emergence of matter in space-time, but exactly how the universe does it remains a mystery.
To create matter over antimatter in the universe, dark or visible, Sakharov imagined that three symmetries would have to be disrupted. The vacuum of the quantum fields in the standard model has a symmetry that preserves the number of particles. So, if the universe starts empty, then it will remain barren unless there is a process that violates the conservation—this is called baryon number violation, or B. But even if we have a process that violates B, nothing stops that same process from producing antibaryons. This is seen in the following example: An electron and positron both democratically interact with a photon. If enough energy in the photon is imparted into the electron’s field, then its vibrational energy will enable the creation of an electron from the vacuum. But, even if you were a demigod trying to create a certain number of electrons in the universe this way, you would necessarily create just as many positrons as well. But if you want to create a universe like ours, there needs to be some way around this. This is Sakharov’s first condition: the baryon number cannot be conserved.
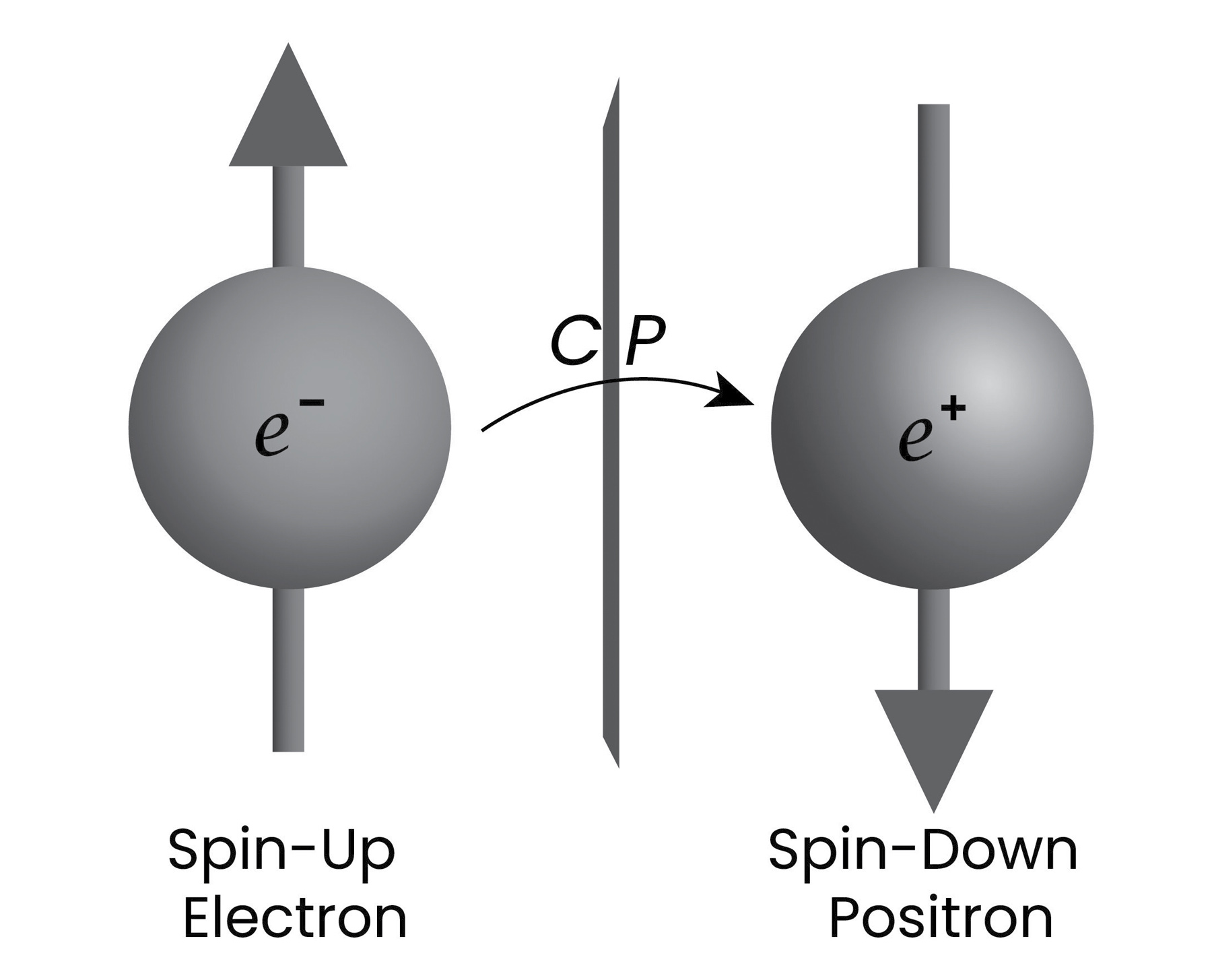
FIGURE 16: Representation of CP symmetry violation in a pair of electrons.
There is another symmetry between the electron field and the photon that also has to be violated. Called CP, where C and P stand for charge and parity inversion, this symmetry is similar to a mirror reflection. When you look in the mirror, there is a spatial reflection that inverts left and right—your left hand looks like your right hand under a mirror reflection. We can imagine CP inversion as a kind of mirror that reflects the charge and orientation of the electron. A spinning particle under a CP inversion sees itself looking like its antiparticle, the positron with its spin reversed. So, if we wanted to create matter over antimatter this CP symmetry would have to be violated. This is Sakharov’s second condition.
The third condition is that both charge asymmetry and particle creation would have to occur out of equilibrium, meaning that creating a particle would have to happen such that the particle would not encounter its antiparticle as they would demolish each other. But when in the history of the universe did these conditions occur for creating matter over antimatter? Attempting to understand the origin of both visible and dark matter points us to an earlier epoch in the early universe called cosmic inflation that had the correct physical ingredients to realize Sakharov’s conditions and a universe that is void of matter for all intents and purposes. We will get to how inflation works its magic creating “something” from “nothing,” but let us return to our discussion about dark matter genesis.
David Spergel and I teamed up with my postdoc and fellow cosmologist Evan McDonough to develop a new theory of dark matter that realizes the coincidence between dark and visible matter baryogenesis while being agnostic about the underlying field theory. We let a quantum consistency condition, known as anomalies, dictate what the nature of the dark matter would be and discovered two pleasant surprises.6 First, we discovered that the dark matter originated from a mirror world of the quarks in our visible world—dark quarks. After they are produced these quarks are close to zero temperature and condense, similar to how helium atoms condense to form a quantum fluid known as a superfluid. The dark quantum superfluid further clumps up under gravitational collapse to make galactic blobs that will differ from ordinary WIMP dark matter. We were surprised about this quantum mechanical result that our calculations revealed, but we were not the first to resort to dark matter as a galactic quantum phenomenon.
Two decades ago, my colleague and friend Wayne Hu, who did pioneering work on relating the CMB fluctuations to fundamental physics, made a quantum leap in our imagination of dark matter. This realization arose from paying attention to a dark secret about dark halos and how they act as a “conductor” for the motion of visible matter in galaxies. There is an entire research enterprise that uses supercomputers to simulate the formation and evolution of galaxies spanning billions of years. These so-called large N-body simulations computationally study the cosmic history of dark matter particles that lead to their formation into dark halos. Time and time again with unprecedented accuracy, large N-body simulations reveal that the distribution of the dark matter in these halos has a cuspyness in its concentration around the center of the galaxy, in disagreement with observations of real halos, whose dark matter distribution is smooth. Hu took this discrepancy seriously and asked what it would take to prevent the dark matter from clumping in the center of galaxies. And his answer was both simple and struck a conceptual resonance with how Newton connected the falling of the apple to the motion of the moon. Hu saw that the same wavelike property that stabilized the electrons’ orbit in the atom can prevent dark matter from forming cusps, if the dark matter had a quantum wavelength on the scale of a galaxy!
Recall that the de Broglie hypothesis says that a massive quantum particle should have a wavelength inversely proportional to its mass. This means an extremely light particle will have a long quantum wavelength. The reason we don’t see the wavelike properties of particles like electrons and protons is because their masses are large enough that their de Broglie wavelengths are microscopic. What Hu argued is that the dark matter can have a quantum wavelength on the scale of a galactic distance provided that it is light enough. And like a galactic electron the light dark matter will not collapse to the center of the galaxy.
Unlike the plethora of possible WIMP particles, so far there are only two potential candidates for superfluid dark matter, a particle that we’ll discuss later called the axion and the dark quark condensate. We are still trying to find new, clever ways of unveiling the true identity of dark matter, assuming that it is a form of matter that doesn’t interact with matter that we see. In the case of superfluid dark matter, we can exploit its quantum properties as a way of distinguishing its properties revealed in the sky. And one unique property of superfluids is that they produce quantum excitations called vortices, which have a mathematical pattern similar to how clouds spiral to make the eye of a storm. If galaxies have vortices in them then they would affect the gravitational lens effect and lead to an anomalous observable signature. Currently, research groups, including my own, are using machine learning to hunt for substructure such as vortices within dark halos as a smoking gun signature of the quantum nature of dark matter.