11

A COSMOLOGIST’S VIEW OF A QUANTUM ELEPHANT

We don’t have to get to some altered state of mind or enter a wormhole to see how mysterious the universe is—it’s right in front of our faces. Our electronic devices are controlled by quantum effects of electrons, and yet, we still don’t have a clue about what the ghostly electron is doing as it approaches the two open holes in the double slit experiment. It does something, but whatever it does, it seems like our mind’s eye is unable to visualize or conceptualize it. The uncomfortable picture is that the electron behaves like a wave when we are not looking at it, and not just a material wave but a wave of potentiality—it’s as if some invisible puppet master is playing tricks on us. If we try to interrogate the electron at the two open slits, where we expect it to be doing its witchcraft, it goes back to behaving like a particle, and the interference pattern is lost. Another equally weird situation is when two spinning electrons are entangled and separated at far distances. We still don’t know how one electron can instantaneously know that the other’s spin was measured to always have the opposite spin of its distant partner. Quantum theory predicts this spooky action at a distance but refuses to tell us how it happens. In other words, the math says that the spins should know about each other at infinite distances, but the math doesn’t simply provide a mechanism. These unresolved issues in quantum foundations have led some physicists, including Einstein himself, to believe that quantum mechanics is incomplete. However, as far as precision experiments can tell, all the predictions of quantum mechanics, no matter how bizarre, have been confirmed.

To me what is bizarre is how this real world, with planets, people, and falling apples, emerged from an underlying virtual quantum universe in the distant past. As I will soon discuss, we have strong evidence that our entire universe in its infancy was quantum, and it evolved to generate our macroscopic world. The paradox can be simply stated as: What measured the wave function of the universe? A first step to understanding the magical emergence of our classical world is to ask how quantum mechanics and Einstein’s description of gravity and space-time can be merged.

We discovered that when the gauge invariance principle is united with special relativity and quantum mechanics, we have a pathway to unify three of the four forces. We arrive at a unique quantum field theory called the standard model that puts all three forces on the same conceptual and mathematical footing. For decades physicists have been challenged in uniting gravity with quantum mechanics. Here is the elephant in the room: it is space-time that would be the state that will exhibit superposition. So, what does it mean for a region of space-time to have many superpositions? Despite this and a handful of potential conceptual questions, there is good reason to invite the quantum into space-time, since quantum mechanics has a history of resolving the singularities and instabilities found in classical physics. Classical general relativity, which is home to even worse black hole and cosmic singularities, seems to be begging for a quantum rescue. What is the culprit that makes quantum gravity so difficult? We must go into this abyss as we expect the final theory of quantum gravity, if it exists, to see what’s behind the black hole singularity and what happened before and at the birth of our universe. For me, quantum gravity holds the promise to give us a new view of our universe far beyond our current imaginations. Maybe we will be able to make sense of the hidden variables that Einstein was after.

First, it’s useful to understand the two main doorways into quantum gravity: background independence and emergence. Background independence is a strong version of the principle of invariance. Recall that the principle of invariance is a key concept in all four forces, but it has a special role in general relativity: invariance operates differently in gravity. The differences give us the first key as to why quantum gravity differs from the successful quantization of gauge field theories like the standard model.

We use coordinate systems to describe the position and motion of an object, but according to the equivalence principle, the reality of the object should not depend on the coordinate label given. We could use any other coordinate system to describe the same particle. Einstein realized that the laws of physics should not depend on the choice of a coordinate system—this is the principle of general covariance, an invariance principle for coordinate systems. The invariance of coordinates is analogous to the name given to a person. Suppose there is a person whose name is John. In Spanish, his name is Juan. In Portuguese it is João. Regardless of the various translations of the name, they are just labels for the actual person, who is independent of the translations. So, if we can describe the location of things with a coordinate system, then different “translations” or choices of these coordinates are all equivalent ways of describing the location of the thing. In principle, there is an invariance encoding the infinite number of ways we could label the position of an object at a point in space-time. We call this diffeomorphism invariance, and it is at the heart of the relativity principle.

Loop quantum gravity is a successful background-independent formulation of quantum gravity. It was pioneered by Abhay Ashtekar, Carlo Rovelli, and Lee Smolin, whose trick for quantizing gravity was to reformulate general relativity so that the background independence is formulated as a gauge theory (like the standard model of particle physics) and to implement similar gauge theory methods of quantizing as was done in the strong interactions of quarks—that is, in quantum chromodynamics. A gauge field can be quantized by having it wrap around a closed loop, like a lasso. The wrapping of a concentrated amount of gauge field flux around a loop is known as a Wilson loop, named after its inventor, Nobel laureate Kenneth Wilson, and it was used to understand how quarks confine in the strong interactions. We can think of Wilson loops as tubes that carry electric flux—lines of a concentrated electric field. The idea is that two quarks are attached to each other by a string of flux. Similarly, gravity is equipped with its own gauge field called the Ashtekar connection. This connection is the key ingredient behind quantizing gravity, and it leads to the remarkable conclusion that the basic building blocks of LQG are atoms of space-time called spin networks, invented by Roger Penrose. These networks join to make quanta of area and volume that have the size of the Planck length—a minuscule distance defined by quantum theory as roughly .0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​0​1​6 meters. If this is the case, then it points to a way to tame the ultraviolet infinities found in quantum field theory since quantized space has a minimal distance and energy.

Another interesting feature of spin networks is the quantum nature of time. When a spin network undergoes a quantum transition it corresponds to a change in time, which ticks as a quantum by a billionth of a trillionth of a trillionth of a trillionth of a second!

Since LQG is a fundamentally discrete structure, one of the big questions is how to recover the smooth space-time that we see in our macroscopic world—this is called the semiclassical limit. In ordinary quantum mechanics the Planck constant is the parameter that turns quantum effects on or off. So, by setting the Planck constant to zero we expect to obtain classical physics. However, this logic does not work in LQG, so some other scheme is needed to get back classical space-time. There have been a handful of proposals to get back classical general relativity from LQG, but it is still at the level of current research. I think that if LQG is to be a successful theory of quantum gravity it should not only tame the black hole and cosmological singularities and recover the good predictions that we already see in general relativity but also connect with some unsolved problems in particle physics.

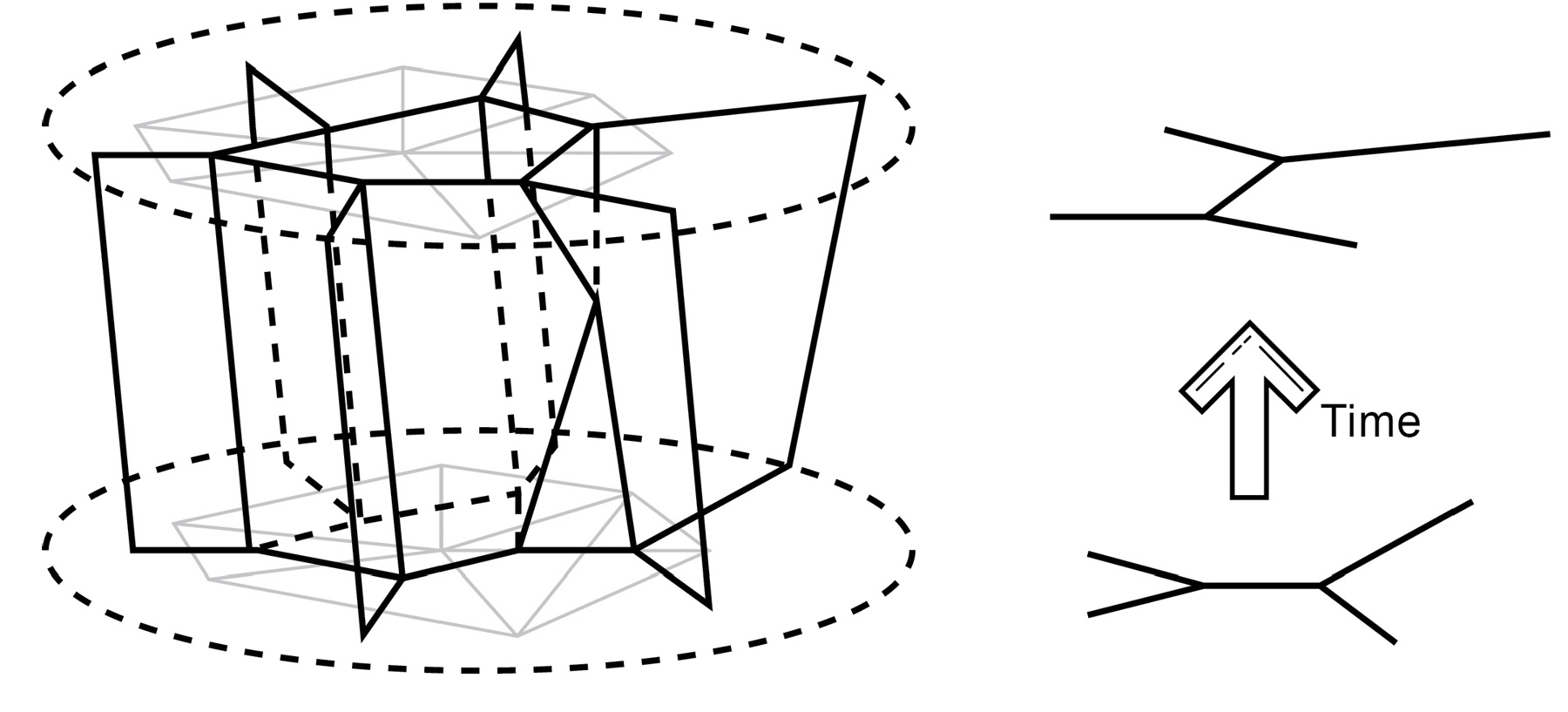
FIGURE 21: A spin-foam transition from one spin network to another depicting quantized time steps.

One question my colleagues and I have been pursuing is how to connect the classical limit of quantum gravity to be coincident with particle physics. One exciting prospect is the realization that the Ashtekar variable, a key ingredient in allowing classical gravity to become LQG, enjoys a broken symmetry that is identical to the weak force. Is this a coincidence? As I was reminded by my mentor, Nobel laureate Leon Cooper, “If we knew what we were talking about, we wouldn’t call it research.” I vividly remember the moment I realized this coincidence between the weak force and gravity as a young faculty member at the Institute for Gravitation and the Cosmos at Penn State. It was actually a simpleminded insight that related a coincidence that the symmetry group of the weak force and general relativity, in the Ashtekar formalism, were the same, though these two forces should have nothing to do with each other. But the genesis of the intrigue occurred during my days at the Stanford Linear Accelerator Center; I had always been puzzled about the origin of parity violation in the weak interaction.

Parity, as we saw when discussing baryogenesis, is a symmetry transformation that is analogous to looking in a mirror. When you look at your left hand in the mirror it is identical but gets converted to a right hand. Parity is a transformation that also inverts an object, turning it upside down. For example, parity would transform a spinning ice skater into an upside-down ice skater spinning in the opposite direction. All the forces were thought to be invariant under parity transformations. In other words, if we look at the scattering of a left-handed quark with a left-spinning gluon field it would occur at the same probability as a right-handed quark interacting with a right-spinning gluon field. The big surprise was that the weak interaction allowed interactions with one-handedness.

While it seems that the violation of parity is inconsequential, life would not exist without it. The parity violation in the weak interaction is at the heart of all nuclear decay processes as well as the chain of subnuclear reactions necessary for fusion. The sun relies on the nuclear fusion of two hydrogen atoms to make helium to provide the energy necessary for life on Earth. So, there would be no life as we know it without parity violation. Sheldon Glashow, Abdus Salam, and Steven Weinberg were awarded the Nobel Prize for constructing the correct theory of the weak interaction and uniting it with the electromagnetic force. However, in their model of the weak force the parity violation was assumed, and there was no deep reason as to why parity violation emerged from some deeper theory and how it would do so. My supposition from the resemblance of the Ashtekar connection of general relativity was that parity violation in the weak interaction came from quantum gravity itself.

So, what does one do when an idea appears that seems crazy and too speculative? Well at the time, my strategy was to go to the source, Abhay Ashtekar, the inventor of the Ashtekar variable.1 Ashtekar has a reputation for being an extremely technical and detail-oriented kind of theoretical physicist, which he combines with laser-sharp intuition. So, if you have an idea and take it to Ashtekar, expect to walk out with your idea in a coffin to be buried in mathematical soil. I knew of young physicists who would be very careful to iron out any technical details before talking with the master. But for some reason, Ashtekar always gave me a hall pass. He treated me as if I had something to say even though my ideas were often raw and inchoate. So, I felt comfortable telling him the idea. After a few minutes, he told me that he didn’t notice this connection between parity violation in gravity and the weak force and encouraged and challenged me to pursue the idea. After months of calculations and thought experiments, I developed a theoretical model to explain the weak interactions parity violation as a gravitational phenomenon.

One of the assumptions behind LQG is that the quantization of gravity does not immediately take matter into account, especially fermions. Recall that all known matter fields are fermions, and they are special because they obey the Pauli exclusion principle. Fermions have a geometric aspect to them since they also carry information about the twistiness of space-time, a quantity called torsion. In present versions of LQG, torsion is assumed to be negligible—what physicists call vanishing. But if LQG is to properly speak about fermions then it may have to relax the assumption of vanishing torsion. Fermions are special because the reason your hand does not go through a table is due to the exclusion principle, which states that no two fermions can occupy the same quantum state. So, macroscopic objects exist because fermions, like protons, neutrons, and electrons, completely evade occupying the same place. I believe that if LQG is to have a hope of having a semiclassical limit, it will come from the simultaneous emergence of the exclusion principle from a quantum foam where fermions are not exclusionary. In other words, space-time becomes fuzzy when fermions lose their special exclusionary powers, but some new, as yet to be discovered, physics makes the fermions transition from being nonexclusionary—“fuzzy”—to occupying different points in space-time, linking the fermions’ distribution to the emergence of classical space-time.

FIGURE 22: A representation of torsion in loop quantum gravity.

As I said, LQG isn’t the only way that I have tried to understand the elephant of quantum gravity. Recall that our access to the quantum world starts from first considering a classical system and applying quantization to it. As in the case of the standard model and LQG, we can quantize by writing down the relevant equations of the classical system and employing the rules of quantization given by Paul Dirac and Richard Feynman. In the case of string theory, which was first proposed to explain certain patterns in the strong interactions, a remarkable surprise presented itself. Take the description of a string of energy that sweeps out a two-dimensional sheet in space-time. We write a mathematical description of the energy for this string, and we can quantize it the same way we quantize a particle. Naturally, the quantum vibrations of the string come with a richer structure than its point-particle cousin. Like a point particle the quantum string will come in a superposition of vibrational states. However, the string will also have other types of oscillations that are unique to its extended nature.

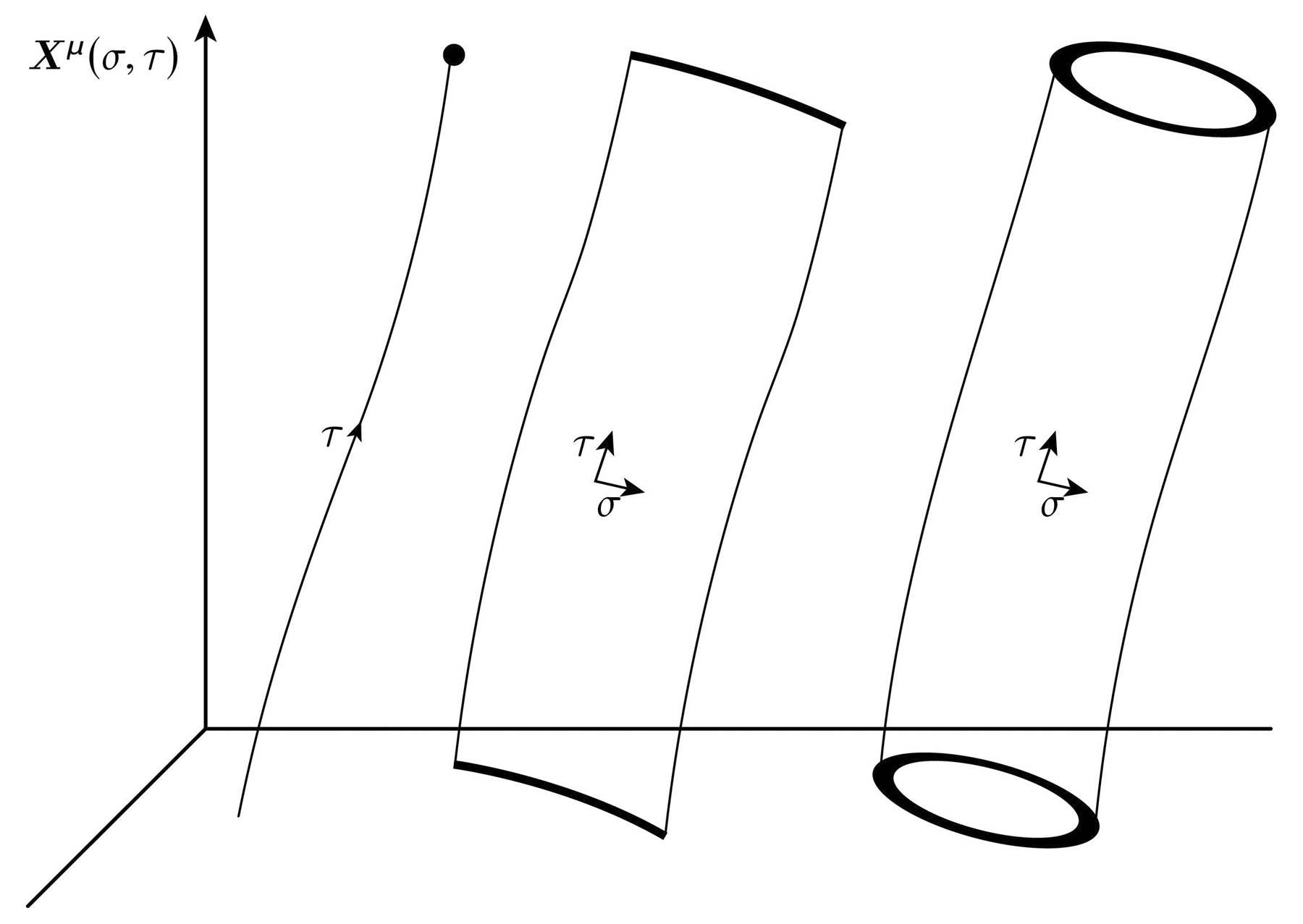
FIGURE 23: Three representations of the key entities in string theory. To the left, we have a point particle sweeping out a world line. In the middle, we have a world sheet of an open string. To the right, we have a world sheet of a closed string.

There are two types of string oscillations, massless and massive. The big surprise to the quantum gravity researchers was that the massless string oscillation includes a spin-2 particle. The only known massless particle with spin 2 is the quanta of the gravitational field, otherwise known as the graviton. This was the first indication that string theory is not what the early string theorist ordered—a theory of the strong interactions. String theory contains quantum gravity.

Even more remarkable is another stringy quantum effect. When a string moves, it can emit a string that propagates and rejoins the original string. This is known as a loop effect, which has a generic effect in quantum field theories to change the strength of interactions. In quantum electrodynamics, a loop effect changes the strength of the interaction between electrons, and this effect has been measured in the lab. In string theory, the same thing happens, but, unlike particle field theories, an invariance that is unique to strings is violated because of the loop effect.

String theory enjoys a symmetry that leaves the physics of the string invariant when we zoom in on the string with a magnifying glass. This symmetry, called conformal invariance, is analogous to the image of a fractal, a pattern that repeats itself regardless of how many times one zooms in or out of the pattern. This symmetry is sacred for strings and must remain intact when the string becomes quantized, otherwise the sacred conservation of probability is destroyed, rendering the underlying quantum theory to make nonsensical predictions. But when the quantum loop effect is considered in string theory, this scaling symmetry appears to be violated. Astonishingly, the loop effect in string theory generates Einstein’s theory of general relativity so as to restore the hallowed conformal symmetry of the string. Amazing! We start out with a theory of a string with no gravity, turn on quantum effects, and general relativity pops out. Master string theorist Edward Witten once said that if we knew nothing about general relativity and knew string theory, general relativity would be a prediction.

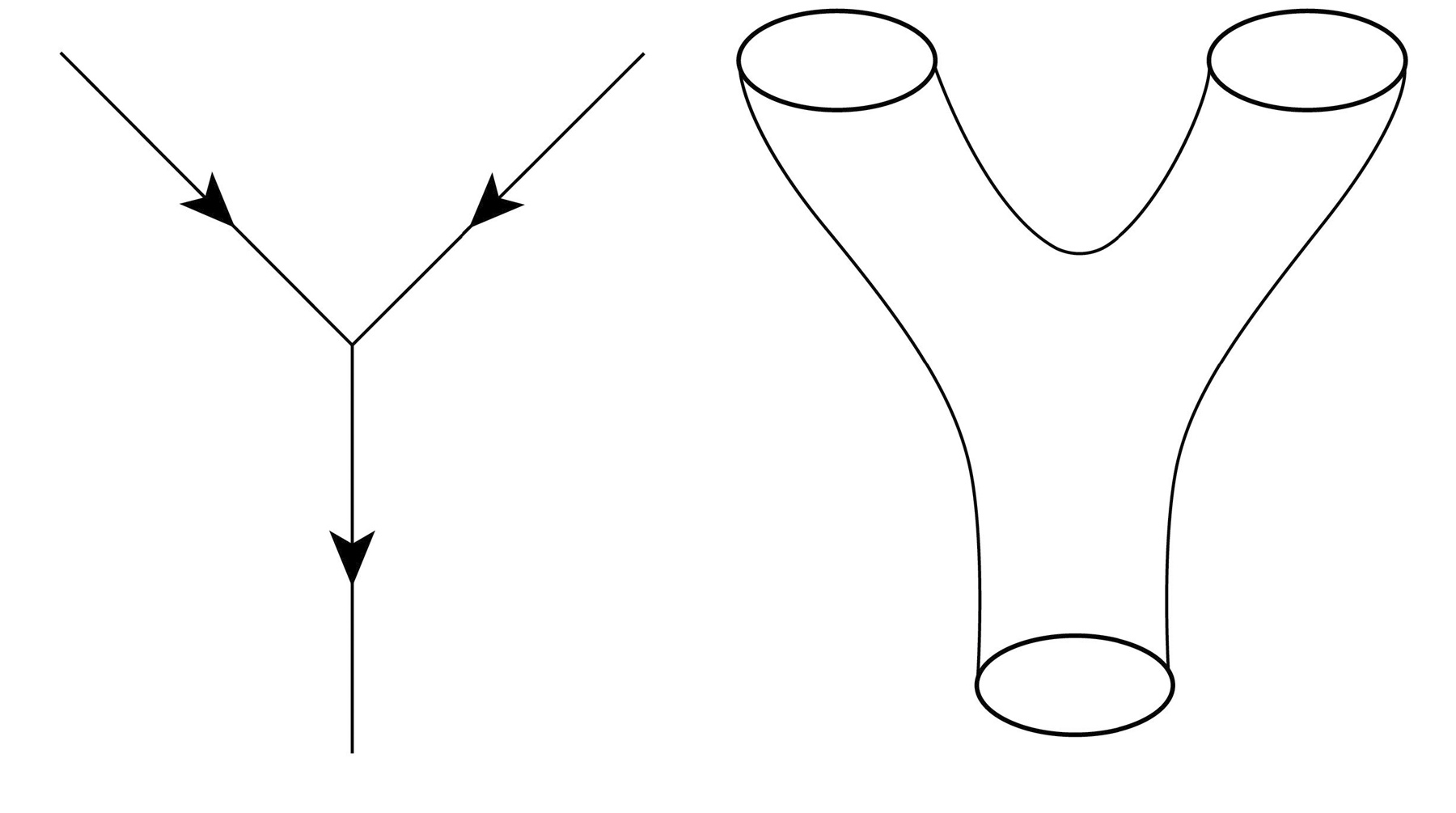
FIGURE 24: Schematic representation of gravity emerging from a string.

For string theory to be quantum mechanically consistent, the resulting theory of gravity must live in ten dimensions. Many physicists have lamented that we live in four dimensions, therefore string theory makes the wrong prediction about the dimension of space-time. However, the extra dimensions in string theory address another mystery found in general relativity and the standard model: What is the origin of the matter fields in our universe? One of Einstein’s final efforts for a unified field theory was to extend the notion of geometry of space-time for matter fields. He adopted an idea first developed by Theodor Kaluza and Oskar Klein, who showed in the 1920s that a five-dimensional theory of gravity seen from a four-dimensional perspective is equivalent to Einstein’s theory of gravity and electromagnetism. The electromagnetic field is realized as the fifth dimension curled up in a small circle. How does that work? The gauge field, whose quanta is the photon, contains all the information about electromagnetism and arises from an invariance of the photon moving on a circle, which is identified with the symmetry of the extradimensional circle. This is a wild idea—that space can cast itself as electromagnetic fields like a shadow in lower dimensions. Of course, the question of what sets the size and stabilizes the radius of this fifth dimension remains open, and we will return to this issue when we discuss the role of string theory in the early universe. Nevertheless, using the same logic as Kaluza and Klein, we see that the ten-dimensional gravity theory in string theory tells a similar story. The extra six dimensions will carry the information about both the matter and the three force carriers of the standard model.

Because common sense and experimental evidence so far both point to a four-dimensional world, string theory must somehow provide a way to understand why we cannot move through the extra six dimensions and why they are not visible. One criterion is that the extra dimensions are microscopically small. This condition leads to a rich set of predictions. Like the Kaluza-Klein theory, the geometry of the extra dimensions manifests itself as the fields of the standard model. String theory starts to look like both a theory of quantum gravity and a unified field theory. But there are some challenges that have faced string theory for decades. First, on top of the fields of the standard models, string theory also predicts a very large number of other fields called moduli that have not been observed. These moduli are fields that govern the sizes and shapes of the extra dimensions that we do not observe in our low-energy world. String theory comes very close to giving us the field contents and symmetries of the standard model. Recall that the standard model did not give us any information about the coupling constants and masses of the particles. Fortunately, string theory moduli can set the values of these parameters. Since these moduli are dynamical fields in string theory, then what kind of physical mechanism fixes them to the values that are observed in the standard model? If we are to believe that string theory is the answer to reality, then what became of these uncountably large moduli fields?

What I personally find very promising about string theory, despite its issues in giving us a realization of our four-dimensional world, is that it naturally encodes the emergence principle. As we saw earlier, we start with a theory of strings with no gravity and it spits out the equations of general relativity and gauge theories (albeit in ten dimensions) when the string experiences quantum corrections. Also, there are realizations in string theory (and loop quantum gravity) from which gravitational theories emerge holographically. Holography, invented by Gerard ‘t Hooft and Leonard Susskind, is the idea that physics is encoded in a space that is one dimension less than what is experienced. According to the holographic principle, our experience of this four-dimensional world is actually an illusion, and the information is encoded in a three-dimensional screen that lives at the boundary of the four-dimensional world. A good geometric realization of this is to imagine that our world is a three-dimensional, solid ball. Then by holography all the information about the ball is actually encoded in the two-dimensional surface of the ball, not in its volume. Exactly how the three-dimensional world is reconstructed depends on the exact nature of the model at hand. Hints of the holographic principle were inspired by laws of black hole mechanics discovered by Jacob Bekenstein and Stephen Hawking. They found that for a black hole the entropy did not depend on the volume within the black hole but the area of the horizon. The information of the relevant degrees of freedom was found to be residing on the two-dimensional surface of the black hole and did not care about its interior.

String theory realizes holography by using the correspondence principle that Niels Bohr argued for in quantum mechanics. In string theory there are two theories that are complementary, or dual, to each other. One theory is a nongravitational conformal field theory (CFT), actually a theory of gauge fields, like the ones found in the standard model but with a lot more symmetries. This gauge theory is complementary to a theory of gravity with maximal symmetry with a negative cosmological constant, known as AdS. Since its inception the duality has passed every nontrivial test of the equivalence between these two theories. Taken literally, this means that gravity emerges from the dynamics of the CFT—which itself has no gravity. The string theoretic realization of holography was invented by the Argentinian physicist Juan Maldacena. I remember when Maldacena, at the time a postdoc at Princeton, wrote this first groundbreaking paper in 1997 now referred to as the AdS/CFT correspondence. The AdS/CFT duality relates a gravitational theory to a space-time called AdS, which is a homogenous and isotropic space-time with a negative cosmological constant. I was a graduate student and wondered how he set up the string theory calculation to realize the holographic duality. The paper quickly got international acclaim, and up to today its impact and number of citations by others have not lost steam.

Whatever quantum gravity will look like, I’m convinced that holography will play a key role.