5
EMERGENCE
A handful of elements from the periodic table come together to create living things like you and me. Yet, the elements themselves are lifeless. How does life emerge from these building blocks? This question is at the heart of emergence. The first two principles we discussed, invariance and superposition, combined to give us the quantum fields we recognize as the building blocks of matter and subatomic forces. Following Paul Dirac’s prediction of the positron, new symmetries in nature were discovered as shorter distance scales, and these new symmetries were experimentally probed with high-energy particle colliders. And these symmetries also functioned to specify the nature of the interactions that fields exhibited with other fields and their associated zoo of particles.
Throughout the last century, physics has been dominated by the quest to identify the natures of those subatomic forces and a theory of everything that unifies them. The idea has been that one day we would be able to find all the fundamental building blocks of the universe, as well as the rules for their interactions. This approach is referred to as reductionism, and is essentially motivated by trying to figure out how to build the universe from the ground up. Superstring theory is an example of such a unified theory. In string theory, the basic building blocks are one-dimensional strings. However, even if we were able to discover such a unified theory, it isn’t clear that it would be able to explain phenomena such as life or consciousness. To the contrary: there’s a very good chance that the fundamental theory could not arise from a reductionist approach.
So we are at a crossroads. On one hand, a major program of twentieth-century physics took us down the successful road of reductionism. The symmetries that were discovered informed us about the patterns and relationships between the elementary forms of matter and the precise ways that they interacted with each other. Indeed, the notion that what is fundamental became synonymous with unveiling more symmetries, at least to some leaders in physics, and that perspective played a prominent role in my own career. I was just starting my dissertation work using the exotic symmetries in superstring theory to solve some of the problems in early universe cosmology. We know from astrophysical observations that the universe is expanding. At the earliest stages of the universe’s history, its environment was exceedingly energetic, hot and dense—conditions not at all unlike those at a collision of particles in a collider like the Large Hadron Collider (LHC). So, from the patterns found in collider experiments, we expect that these symmetries generated by superstrings were activated in the very early universe, where superstrings are expected to be the key players. My thesis exported a special symmetry from string theory into cosmology, called target space duality, or T-duality, which treats the physics in a large region of space and a small region of space as being the same. So, as we approach the big bang singularity, where the universe approached microscopic distances, we could avoid the big bang singularity with T-duality. The dream was to use cosmology to test unified theories like string theory, or other approaches to quantum gravity. Superstring cosmology is still an important topic in cosmology, and I still devote some of my research efforts in this direction. So far, the expectation to unveil more symmetries at the shortest distance scales works theoretically.
On the other hand, there were clear failures of the reductionist regime in particle physics. One of the most famous examples of emergence in quantum physics is superconductivity—really, it’s the poster child of emergence in physics. In 1911, Nobel laureate Heike Kamerlingh Onnes observed that when he lowered the temperature of a metal close to absolute zero, the electric current would flow with zero resistance. There was no reason to expect how and why the billions of electrons, which repel each other as well as experiencing impurities in the metal, should superconduct. After all, lowering the temperature does not seem to prevent the electrons from repelling each other or get rid of the impurities in the metal. Many great physicists, like Einstein, Schrödinger, Heisenberg, Lev Landau, and Feynman, worked on superconductivity. During this time, many thought that completely new physics was needed, perhaps a new law, to account for superconductivity. And it took forty-six years for the trio of John Bardeen, Leon Cooper, and John Robert Schrieffer (developers of the “BCS” theory) to show that good old quantum mechanics and electromagnetism were enough. Superconductivity doesn’t supplant them. It emerges from them.
The Principle of Emergence: Systems with interacting elementary constituents can exhibit novel properties that are not possessed by the constituents themselves.
The reason I am promoting the phenomenon of emergence to a principle is based on Einstein’s criteria for a principle, because, to borrow his words, “[A principle is realized by] perceiving in comprehensive complexes of empirical facts certain general features which permit of precise formulation.” What are the complexes of empirical facts in emergence that can transcend its context? There are many examples of disparate and seemingly unrelated physical and biological systems where we see emergence. Emergent behavior also happens in populations of living organisms. Groups of ants can collectively build a bridge of ants so that others can cross a barrier of water. The origin of life itself is argued to be an emergent phenomena. A unicellular bacteria has autonomous properties, such as motility, replication, and metabolism that its individual molecules, like proteins, do not exhibit.
But what is at the heart of emergence? How does a system “know” to exhibit novel collective behavior? These are hard questions that are currently being researched, and there are some partial answers. A universal aspect of emergence is the relationships between the emergent system and the parts that make it up. Although the emergent property is novel relative to its constituents, there is an interdependence between the emergence and the constituents. For example, the system of atoms that gives rise to an emergent liquid property depends on the collective behavior of the individual atoms. However, in the solid state, the atoms are on average located in a repeating array, forming a large-scale crystal. A simple example of emergence can be seen right in front of your face.
The renowned theoretical physicist Nigel Goldenfeld, who now directs an institute that focuses on finding links between emergence in physics and biology, has an experiment that we can all do to demonstrate an emergent phenomenon. Here is how it goes. First, push your hand forward in empty space. Second, get a chair and push the chair until it falls on the floor. The fact that the chair moved and fell on the floor is emergence at work.
This might sound strange, but it’s true. When you moved your hand, it was interacting with the air, which is actually a fluid made up of air molecules. The chair, on the other hand, is a solid. The atoms of the fluid and the solid obey the same laws of atomic interactions, yet, despite the sameness of their atomic interactions, the solid state has new emergent laws of physics. That is, it has new long-range forces, such as a rigid elastic response from your hand pushing against it. The origin of these new forces in the solid state arises from the statistical properties, or collective behavior, of the billions of atoms. If we work at the level of the description of the solid, we can’t deduce what the underlying interactions of the atoms are. At the level of the solid state, all we can deduce is that the continuum description, rigidity, elasticity, and so on emerges from the collective behavior of the atoms.
The same goes for superconductivity. What I find interesting in that story is how BCS hacked superconductivity, not just because it’s interesting science, but because it gives some guidance for current problems that we are trying to solve. After all, some of the problems that we consider to be impossible to solve have been around for a shorter period than superconductivity.
I had the good fortune to hear some of the story of superconductivity directly from Leon Cooper, who was my first PhD adviser before I changed fields to quantum cosmology. During my first year of graduate school, I didn’t know who Cooper was, and no one told me that he had won the Nobel Prize. He had the flair of a Shakespearean actor, wore fine Italian suits, and sported shades on a well-groomed head of jet black, wavy hair. During our weekly departmentwide talk, where famous researchers would present their results, Cooper would sit at the front of the room and ask what seemed to be naive questions, the type a schoolchild would ask. And this was exactly the quality of mind that, among other things, enabled him to access the ingenuous insight that would crack the nearly fifty-year-old problem of superconductivity.
Superconductivity was couched in the subfield of the physics of solids, known as solid-state physics.1 One of the leaders of the field, John Bardeen, who previously shared a Nobel Prize for the discovery of the transistor, had been tirelessly working on superconductivity for years with no luck. Bardeen was well aware of the decades of failed attempts to explain superconductivity, and he decided he had to get an outsider’s perspective and tools to bring new life to the problem. So, he sought out a theorist that had a fresh pair of eyes and wasn’t jaded by the biases that may be formed by experts in the field.
I remember the serendipitous early summer day I was driving from Hanover, New Hampshire, to New York City and decided to stop by Brown with the hopes of seeing Professor Cooper. It had been almost a decade since I had seen him in person. I caught wind that he was retiring (but still fully engaged in research, as he still is). During summers, many faculty are traveling to conferences, but when I got to the physics building at Brown, Cooper was there in his spacious office, filled with books and covered with blackboards, doing a calculation. We sat down for a chat. He immediately asked me what I was working on.
I thought that I was going to impress him with my new take on the matter-antimatter asymmetry in the universe. Cooper stopped me and said, “You should find a real problem and solve it. Many people put their hands up in surrender when a problem gets too hard and claim it’s impossible.” I took this to be both a challenge and validating. What might at face value look like Cooper’s rejection of my idea I took instead as him holding me to a higher standard and the expectation to solve a big problem. Even today, I try to live up to my former adviser’s version of tough love with my students—to recognize and help awaken their hidden talents. Up till that point, I was playing it safe and avoiding physics problems that I thought only the most able of physicists should have the permission to work on. I asked Cooper, “How did you solve superconductivity?” What he said gave me some strategies for approaching my own problems.
Cooper went on to tell me that he was trained in another field, theoretical particle physics, and had mastery of the techniques new to that field, such as Feynman diagrams. When he was invited to work with John Bardeen in condensed-matter physics, as the field working on superconductivity was known, he had an unsullied and less-biased take on the nature of the problems those physicists were facing. For one, as we’ve seen in this book, particle physics concerned itself with discovering the nature of subatomic forces by exploiting the quantum scattering processes between elementary and nuclear particles. Solid state environments concern the behavior of billions of interacting electrons in an environment filled with other atoms usually organized in the form of a periodic crystal lattice. Superconductivity was both a conceptual and mathematically technical dragon to slay. One major obstacle was that the problem seemed to require solving the Schrödinger equation for a wave function of billions of electrons interacting with a lattice of metallic atoms—the many-body wave function. No one working on the problem, no matter how technically skilled, has been able to surmount the mathematically crippling wall of solving the many-body wave function. According to Cooper, Bardeen “omitted to mention that practically every famous physicist of the 20th century had worked on the problem and failed.”2
Cooper quickly encountered the daunting and insurmountable equations. On a seventeen-hour trip to New York City, he tirelessly tried his extensive bag of mathematical tricks but got nowhere. He ran out of technical steam and started feeling that the equations were preventing him from seeing the root of the problem. So he decided to step back from the equations and think intuitively about the problem. And then he made a simple and ingenious guess. Part of his mental wizardry was to simplify the problem and avoid unnecessary details, decisions geared toward making the problem more tractable.
As a hint into Cooper’s insight, recall that electrons carry a tiny magnetic pole. This pole can also obstruct their motion, say when they are flowing in a current, due to the magnetic forces of surrounding electrons, which cause deflection and electrical resistance. It seemed that, if superconductivity were going to be possible, then the golden rule that electrons necessarily repelled each other had to be broken. Cooper realized that if the electrons could pair up, with their spins oppositely aligned, then the members of each pair would lose their identity as electrons, and their overall spin would vanish, mitigating the local resistance. An emergent phenomenon, the Cooper pair, was born. But the grouping doesn’t stop there. When all the electrons pair up, they clump together to collectively behave as one object and move in a ghostly fashion through obstructions in the metal. Cooper likened it to a line of ice-skaters, arm in arm: “If one skater hits a bump, she is supported by all the other skaters moving along with [the line].” In other emergent phenomena in condensed matter, this long-range order is a collective behavior of the individual electrons or atoms.
The formation of Cooper pairs led to a handful of other emergent properties in the superconductor. First, in order for the supercurrent to maintain itself, the superconducting environment would have to expel any magnetic field. This observation is known as the Meissner effect and is predicted by the BCS theory—it is the reason magnets levitate above superconductors. The underlying physics in superconductivity was later found in other systems, such as neutron stars. The extremely dense environment of neutron stars enables neutrons to Cooper pair and exhibit the collective behavior of a superconducting fluid, called a superfluid. Another Nobel Prize was awarded to Yoichiro Nambu, who applied the BCS theory to understand the emergence of particles called the pion, which was found to be a Cooper pair of quarks. BCS theory also inspired some of the architects of the standard model of particle physics to think about how mass could emerge from a similar type of symmetry breaking, and we will discuss this in an upcoming chapter.
In a seminal essay entitled “More Is Different,” Nobel laureate Philip Anderson puts emergence at center stage over reductionism in physics: “The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe.… At each stage of [emergence] entirely new laws, concepts, and generalizations are necessary.” Anderson goes on to identify the organizing principle that is behind most emergence in condensed-matter systems, that is, symmetry breaking. When we see symmetries, we often see an underlying pattern of phenomena. For example, in relativity, the space-time symmetry inherent in the laws of motion functions to give relative lengths and time for different moving observers. Emmy Noether proved that symmetries are linked with conservation laws. And symmetry breaking signals new properties that are hidden from the symmetric realm.
To see this, consider a piece of metal, like iron. Like a checkerboard is a repeating arrangement of black and red squares, all metals are repeating periodic arrangements of atoms with electrons waiting to easily flow from one site to the other. At each atomic site the electrons carry a tiny magnetic pole due to their quantum spin. Recall that the quantum spin can either be up or down, reflecting its quantum nature. At high temperatures the billions of the electron spins point in a random direction. If we add all the spins, because of the random orientations, the total spin of the system cancels out to zero. Since the total spin and magnetization is zero there is no preferred direction of all the spins and the system has a symmetry that is invariant under rotations. This means that the iron has a symmetry that is analogous to the symmetry of a sphere. However, as we lower the temperature to a critical value, the spins all on average spontaneously pick a direction, attaining a net magnetic field. This is like balancing a pencil on its tip. As a result, the spherical symmetry is broken by the emergence of magnetism. Not only is magnetism emergent, but the preferred direction that breaks the symmetry creates rigid directions that can support the transmission of magnetic waves. In all the examples in condensed-matter physics, the constituents, such as electrons or other fermions, exhibit cooperative behavior similar to the swarm of ants or bees that collectively perform a task that an individual member cannot accomplish alone.
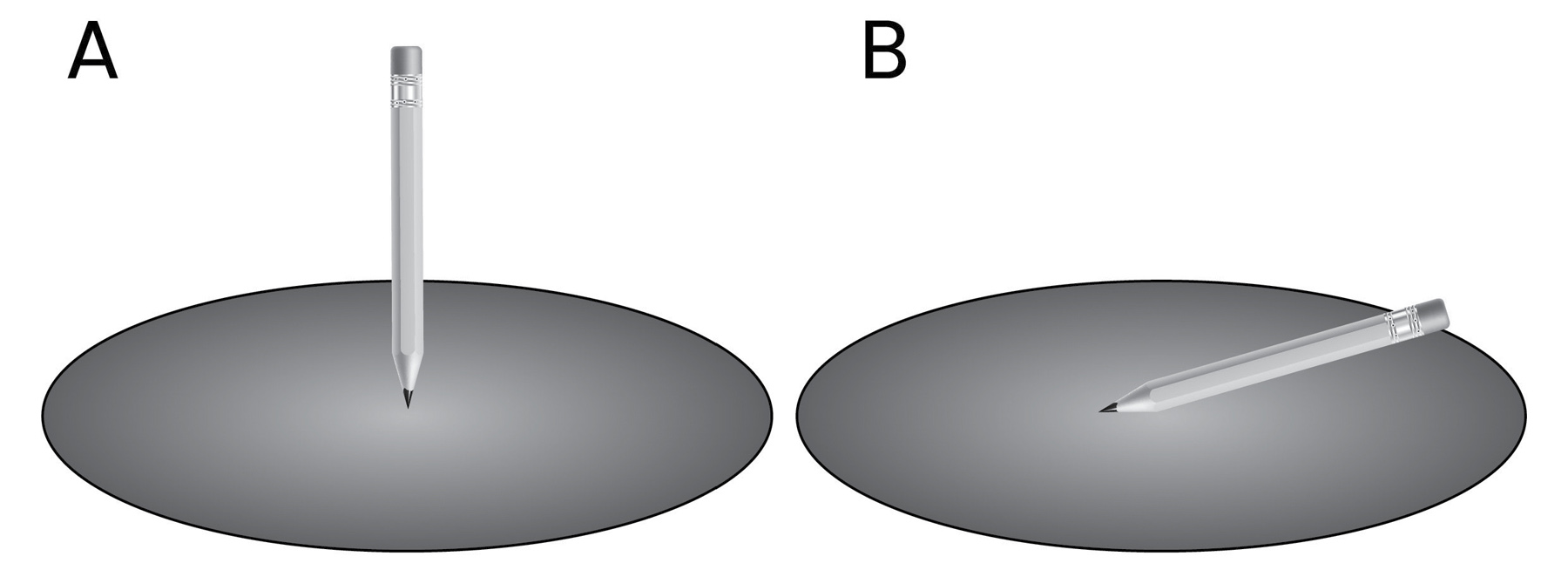
FIGURE 10: An example of spontaneous symmetry breaking. In image A the forces acting on the pencil have a rotational symmetry. However, this system is unstable because the gravitational force in the z-direction will break the symmetry. In image B the pencil picks a direction, which results in breaking the original rotational symmetry. Any direction could have been selected, and this randomness is a sign of the symmetry being spontaneously broken.
In hindsight it was also discovered that superconductivity emerged from the breaking of another type of symmetry, not related to space-time but closer to those found in the fundamental interactions, such as the strong and weak nuclear forces. The principle of emergence and symmetry breaking turns out to be at the heart of important matters in the fundamental forces. As we will explore in the next chapter, the nuclear interactions, such as the weak and strong forces, are governed by symmetries associated with the charges of elementary fields and particles. And the breaking of these symmetries also has essential properties, such as the origin of mass and the emergence of matter over antimatter in our universe. Even stranger is the idea that space and time are also emergent properties. By analogy, these are atoms of space and time whose collective behavior can give rise to the malleable space-time fabric that Einstein discovered.
There has always been a deep interplay between physics and other scientific disciplines like biology, chemistry, and the social sciences, where even more mysterious forms of emergence occur. Does the organizing principle of symmetry breaking seen in physical systems apply to understanding emergence in other domains? Are there other organizing principles that go beyond symmetry breaking? And maybe even beyond physics?