Chapter 6
Forecasting Demand
In This Chapter
 Getting acquainted with the fundamental rules of forecasting
Getting acquainted with the fundamental rules of forecasting
 Predicting demand using various methods
Predicting demand using various methods
 Finding and measuring forecasting error
Finding and measuring forecasting error
How wonderful life would be, especially in the world of operations management, if it were possible to gaze into a crystal ball and accurately predict future events and consumer behavior. Unfortunately, that kind of foresight just isn’t available. The next best thing is a well-developed forecast.
In business, a forecast refers to an estimate or prediction of what is likely to happen in the future. The key words here are estimate and prediction. Without the elusive crystal ball, forecasts, to some degree, are always inaccurate. At best, forecasting is an imprecise science, but not having a forecast to guide decisions about inventory, capacity, and production levels can be fatal to a business.
One of the biggest determinants of financial success is how accurately you can predict demand. If you forecast your demand too high, you may waste resources producing more products than customers will purchase. If you forecast demand too low, you may leave customers disappointed because they can’t purchase your product.
This chapter is all about forecasting demand. We start by introducing the general rules of forecasting and describing the basic types of forecasting models, and then we detail the most popular methods for measuring the error of a forecast.
Getting Savvy about Forecasts
Point forecasts, or single-number predictions of demand, are generally always incorrect. That’s why you need not only an expected value (what you think demand will be) but also a measure of your method’s forecasting error (see the section Acknowledging the Error of Your Ways later in this chapter).
Here are the fundamental tenets of forecasting:
 Aggregated forecasts are more accurate than disaggregated forecasts. Forecasting the demand for a product at a national level is more accurate than forecasting it at each individual retail outlet. The variation of demand at each sales point is smoothed when aggregated with other locations, providing a more accurate prediction. You can achieve a similar improvement by forecasting the aggregate demand for all the variations of a product combined instead of forecasting a single variation.
Aggregated forecasts are more accurate than disaggregated forecasts. Forecasting the demand for a product at a national level is more accurate than forecasting it at each individual retail outlet. The variation of demand at each sales point is smoothed when aggregated with other locations, providing a more accurate prediction. You can achieve a similar improvement by forecasting the aggregate demand for all the variations of a product combined instead of forecasting a single variation.
 Be prepared to change your forecasting model, but don’t overreact to random changes. Demand patterns can and do change, and when actual changes occur, you may need to change your forecasting technique. Measuring your forecasting error can alert you when changes occur; however, you need to verify that a sustainable change has actually occurred and that what you observed isn’t a random variation. (For more on forecasting error, see the section Acknowledging the Error of Your Ways later in the chapter.)
Be prepared to change your forecasting model, but don’t overreact to random changes. Demand patterns can and do change, and when actual changes occur, you may need to change your forecasting technique. Measuring your forecasting error can alert you when changes occur; however, you need to verify that a sustainable change has actually occurred and that what you observed isn’t a random variation. (For more on forecasting error, see the section Acknowledging the Error of Your Ways later in the chapter.)
 Don’t substitute forecasts for known information. Many companies can become blinded by their forecast and ignore what’s actually occurring in the business environment. If something changes, such as a weather occurrence, or more data becomes available, such as a sales order, be prepared to adjust your forecast to incorporate the new information.
Don’t substitute forecasts for known information. Many companies can become blinded by their forecast and ignore what’s actually occurring in the business environment. If something changes, such as a weather occurrence, or more data becomes available, such as a sales order, be prepared to adjust your forecast to incorporate the new information.
 If a simple technique yields acceptable accuracy, don’t use a more advanced technique. Use the simplest forecasting model that provides the desired accuracy. For example, don’t use a model for seasonality unless it gives you noticeably greater accuracy than a simple exponential smoothing model (we describe forecasting models in the next section).
If a simple technique yields acceptable accuracy, don’t use a more advanced technique. Use the simplest forecasting model that provides the desired accuracy. For example, don’t use a model for seasonality unless it gives you noticeably greater accuracy than a simple exponential smoothing model (we describe forecasting models in the next section).
 Select a forecasting technique that makes good use of the available data. The time-series forecasting methods discussed later in the chapter rely on having not only a large quantity of data but also relevant and accurate data. If you don’t have confidence in the amount or quality of the data, you may want to choose a qualitative method to forecast until data becomes available. For example, consider basing your forecasts on potential market size and adjusting based on experience. Applying sophisticated forecasting models to faulty data won’t improve the underlying quality of the data or the forecast.
Select a forecasting technique that makes good use of the available data. The time-series forecasting methods discussed later in the chapter rely on having not only a large quantity of data but also relevant and accurate data. If you don’t have confidence in the amount or quality of the data, you may want to choose a qualitative method to forecast until data becomes available. For example, consider basing your forecasts on potential market size and adjusting based on experience. Applying sophisticated forecasting models to faulty data won’t improve the underlying quality of the data or the forecast.
 Short-term forecasts are more reliable than long-term forecasts. The forecast horizon, or how long into the future the forecast predicts, has a direct impact on accuracy. In other words, predicting the sales for this month is easier than predicting the sales for a year from now. Many things can happen between now and next year, such as new competitors entering the market, customer preferences changing, or new technology causing shifts in demand. These changes become tougher to predict as the forecast horizon increases.
Short-term forecasts are more reliable than long-term forecasts. The forecast horizon, or how long into the future the forecast predicts, has a direct impact on accuracy. In other words, predicting the sales for this month is easier than predicting the sales for a year from now. Many things can happen between now and next year, such as new competitors entering the market, customer preferences changing, or new technology causing shifts in demand. These changes become tougher to predict as the forecast horizon increases.
 There is no single best forecasting technique. The important point is to compare different forecasting models and choose the one that best meets the needs of your situation and matches the data you have available.
There is no single best forecasting technique. The important point is to compare different forecasting models and choose the one that best meets the needs of your situation and matches the data you have available.
It’s important to note that, although disaggregate forecasts can be less accurate than aggregate forecasts, disaggregate forecasts are critical to production planning (see Chapter 9). For example, if a firm produces different models of TVs, production planning at the manufacturing floor level requires a detailed number of how many of each model to produce. By postponing a commitment to the details, the firm can make a more accurate disaggregate forecast (short-term forecasts are more accurate than long-term forecasts). Reducing flow times allows a firm to delay the decision on what exact models to produce, which improves its forecasts.
Building a Forecast to Predict Demand
You have many ways to build a business forecast, and this section describes a few different basic techniques. But before you can even begin building a forecast, you must get a handle on your demand patterns.
Recognizing demand variation
Demand isn’t always consistent; demand can vary for many reasons. Recognizing why demand varies helps you increase your forecast’s accuracy. Specifically, watch for these factors that may trigger variations in your demand:
 Cycles are wavelike occurrences that repeat over longer periods of time. They’re usually tied to economic conditions or the business cycle. Big-ticket items such as automobiles often display this type of pattern.
Cycles are wavelike occurrences that repeat over longer periods of time. They’re usually tied to economic conditions or the business cycle. Big-ticket items such as automobiles often display this type of pattern.
 Irregular variations are changes that result from a one-time event. They’re not representative of normal conditions. A celebrity using a product in public that spurs fans to go out and purchase in mass and the sale of water bottles before a major weather event are examples of irregular variations.
Irregular variations are changes that result from a one-time event. They’re not representative of normal conditions. A celebrity using a product in public that spurs fans to go out and purchase in mass and the sale of water bottles before a major weather event are examples of irregular variations.
 Random variations occur without any known reason or explanation. They’re the unforeseeable and unexpected changes in demand.
Random variations occur without any known reason or explanation. They’re the unforeseeable and unexpected changes in demand.
 Seasonal factors are regular variations that occur over and over and are related to some particular event. Products and services with significant seasonal demand include air conditioners and snow shovels (which vary by time of year) and back-to-school clothing and supplies (which vary according to certain events). Some industries have “seasonal” demand patterns that occur more frequently, such as the weekly increase in customers on Fridays and Saturdays at restaurants. Seasonal factors can sometimes be self-induced, as in end-of-quarter or end-of-year sales or promotions to help a firm make sales quotas.
Seasonal factors are regular variations that occur over and over and are related to some particular event. Products and services with significant seasonal demand include air conditioners and snow shovels (which vary by time of year) and back-to-school clothing and supplies (which vary according to certain events). Some industries have “seasonal” demand patterns that occur more frequently, such as the weekly increase in customers on Fridays and Saturdays at restaurants. Seasonal factors can sometimes be self-induced, as in end-of-quarter or end-of-year sales or promotions to help a firm make sales quotas.
 Trends are a long-term upward or downward movement in demand. When products experience a growth or decline in the market, trends tend to emerge. Examples include the growth of organic products in the supermarket and the decline in sales of paper books in favor of the electronic variety.
Trends are a long-term upward or downward movement in demand. When products experience a growth or decline in the market, trends tend to emerge. Examples include the growth of organic products in the supermarket and the decline in sales of paper books in favor of the electronic variety.
Looking to the past to predict the future
The most popular forecasting model for established products and services monitors demand over time, making predictions based on what’s happened in the past. This method requires past data for current metrics. Two basic techniques —the moving average and exponential smoothing — provide this kind of forecast, and you can modify the basic techniques to account for trends and seasonal fluctuations that often exist in demand patterns.
Tracking the average
The moving average method uses an average of a consistent number (n) of past occurrences to predict the future value. You update the average each time you observe a new occurrence. Calculate the moving average forecast with this equation:

Compute the moving average forecast MAn by summing the most recent past n actual observations (An, An, . . . An) and dividing by the number of observations summed (n).
To give a three-month moving average example, assuming that demand over the last three months has been 1,225, 1,365, and 1,415 units, your forecast for next month (month 4) would be 1,335 units.
As each new actual observation becomes available, update the forecast by adding the newest observation and dropping the oldest. Updating the previous example, if demand in month four is actually 1,455, then the forecast for month five using a three-month average is (1,365 + 1,415 + 1,455) ÷ 3 = 1,412.
An important decision is how many past observations to use in the moving average. The previous example uses three observations and is often referred to as an MA(3) forecast because it’s a moving average with three terms. Figure 6-1 shows the demand pattern for a product with its MA(3) and MA(5) forecasts.

Illustration by Wiley, Composition Services Graphics
Figure 6-1: Comparison of moving average forecasts.
In Figure 6-1, the MA(3) more closely follows the actual demand than the MA(5). This figure also shows that a moving average forecast follows behind the actual data series; the greater the number of observations (n) used in the forecast, the farther behind the actual demand the forecast will be.
Smoothing exponentially
Exponential smoothing addresses the major issues with moving average forecasting by accounting for the error in a forecast. In exponential smoothing, each new forecast (Ft) is simply the sum of the previous forecast (Ft –1) plus a percentage (α) of the difference between the previous forecast and what actually happened (At –1). α is often referred to as the smoothing constant and is always a value between 0 and 1.
This difference between what actually occurred and what was forecasted to occur is the forecast error. We talk more about forecast errors in the Acknowledging the Error of Your Ways section later in this chapter.
The general equation for the next forecast is

Figure 6-2 shows demand for the product that was referenced in Figure 6-1 as forecasted with a smoothing constant of 0.2 and 0.7. At time 25, the forecast for the α = 0.2 series (F25) is 9,120 and the actual observation (A25) is 8,764. The forecast for time 26 (F26) = 9,120 + (0.2)(8,764 – 9,120) = 9,049.
Figure 6-2 shows that the forecast always lags the actual data and that the larger the α is, the more responsive the forecast is to changes in demand. On the other hand, a larger α also makes you more prone to overreacting to random changes in demand.

Illustration by Wiley, Composition Services Graphics
Figure 6-2: Comparison of exponential smoothing forecasts.
Both moving average and exponential smoothing forecasting reveal the effects of changing n and α. When choosing the best technique and parameter value for your forecast, you can set up a spreadsheet with past demand values and calculate what your forecast would have been given different parameter values. Comparing the results of this forecast and what actually happened, you can determine the value that gives you the best forecast. The accuracy, however, relies on your demand pattern holding steady based on the past.
Accounting for trend
Many products experience an upward or downward trend in demand over time. Accurately forecasting demand requires you to recognize when this occurs. If you don’t, your forecast won’t keep up (or down) with the trend.
A popular technique for forecasting demand when a trend exists is trend-adjusted exponential smoothing. The forecast (Ft –1) consists of a smoothed forecast (St) and a trend factor (Tt).
To calculate a trend-adjusted forecast, use this formula: Ft + 1 = St + Tt
Calculate St as
St = Ft + α(At – Ft)
And solve for Tt:
Tt = Tt –1 + β(Ft – Ft –1 – Tt – 1)
You must choose two smoothing constants α for the average and a β for the trend. Be sure to use the same procedure as discussed in the preceding Smoothing exponentially section for choosing a β. You want to use different combinations of both α and β because there may be some interaction between the two. The optimal β can vary based on the chosen value of α.
Figure 6-3 shows the forecast for demand with an α of 0.3 and a β equal to 0.4. For example, at time 10, the forecast (F10) is 137.1 but actual demand (A10) turns out to be 151. From this, the smoothed forecast (S10) is 137.1 + (0.3)(151 – 137.1) = 141.3. You then need to find the trend at time 10 (T10). The trend at time 9 (T9) was 6.0, and the forecast at time 9 (F9) was 130.7. The trend at time 10 (T10) is 6.0 + (0.4)(137.1 – 130.7 – 6.0) = 6.2. From that, you can find that the forecast at time 11 (F11) is 141.3 + 6.2=147.5.
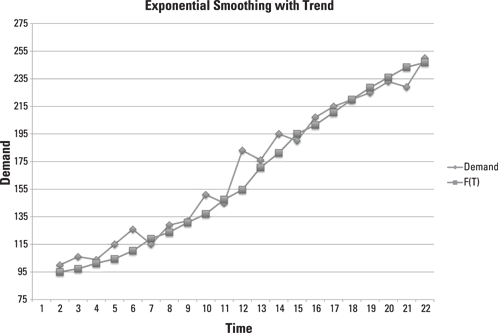
Illustration by Wiley, Composition Services Graphics
Figure 6-3: Exponential smoothing with a trend.
Facing seasonality
Seasonality is the upward or downward movements in demand that are associated with recurring events, such as weather and holidays. The time period for a season can be long or short. For example, sales at movie theaters are generally higher in the summer and around Christmas. Another example of seasonal effects — the use of the term seasonal can be a bit confusing — is the increased number of customers in movie theaters on Friday and Saturday.
When accounting for seasonality, you want to express demand in terms of how much the value varies from the total average. For the movie theater, over the course of one or more weeks, an average number of customers visit per day — X(average). Calculate this average by summing the number of customers over the course of a week and dividing that sum by 7 (the number of days open in the week). You may want to do this for more than one week to get an adequate sample. Then forecast X(average) using the moving average or exponential smoothing technique described in previous sections.
To calculate the movie theater’s seasonality index for each day of the week, take the average number of customers for any one day and divide that number by the X(average). For example, if the theater serves an average of 1,600 customers a day and the average for a Monday is 400, then the seasonality index for Monday is 0.25 (400 ÷ 1,600). On a Saturday, the theater serves 2,400 customers and has an index value of 1.5 (2,400 ÷ 1,600).
After you calculate the seasonal index, you can forecast demand for each day by multiplying the index by the average forecasted demand, X(average). Monitor X(average) to identify any trends you may need to consider for future forecasts and business planning.
Figure 6-4 shows the forecast for a time series that exhibits seasonality.

Illustration by Wiley, Composition Services Graphics
Figure 6-4: Forecasting with seasonality.
Lacking data: No problem
The forecasting methods described in the previous sections require past demand data. In many cases, this data isn’t available. For example, when you introduce a new product or enter a new market, no record of past demand exists for forecasts.
In this situation, you can use qualitative techniques and build causal models to build a forecast.
Relying on qualitative techniques
Without past data, you must rely on judgment and opinion to derive a forecast. The key is to get as close to the customer (or potential customer) as you can. Here are some methods you can utilize:
 Collaborative forecasting: Collaborative forecasting involves gathering information about the marketplace from personnel at all levels of the organization and supply chain. This method works well for long-range planning and new product development.
Collaborative forecasting: Collaborative forecasting involves gathering information about the marketplace from personnel at all levels of the organization and supply chain. This method works well for long-range planning and new product development.
 Customer surveys: Surveying current and potential customers can generate helpful information, but you must be careful when conducting the survey. Proper survey design and implementation could fill its own For Dummies book; it’s beyond the scope of this book. Just be aware that survey information can be misleading.
Customer surveys: Surveying current and potential customers can generate helpful information, but you must be careful when conducting the survey. Proper survey design and implementation could fill its own For Dummies book; it’s beyond the scope of this book. Just be aware that survey information can be misleading.
 Demand patterns of similar products: When introducing new products to the market, looking at demand patterns of similar products in the past can provide a good starting point. Particularly for electronics, most new products seem to follow a similar demand curve as previously launched products in a given category. See Chapter 18 for details on how to manage new product growth.
Demand patterns of similar products: When introducing new products to the market, looking at demand patterns of similar products in the past can provide a good starting point. Particularly for electronics, most new products seem to follow a similar demand curve as previously launched products in a given category. See Chapter 18 for details on how to manage new product growth.
 Direct customer contact: Your salespeople and customer service representatives are your lifeline into what customers are thinking. Direct input from customers provides the best information on potential demand when trying to forecast.
Direct customer contact: Your salespeople and customer service representatives are your lifeline into what customers are thinking. Direct input from customers provides the best information on potential demand when trying to forecast.
Identifying related variables
Another way to forecast demand for a product is to find correlations in demand between your product and other products. For example, demand for electric vehicles may exhibit a relationship with the price of gasoline.
Here, you can use a simple regression model which represents the statistical relationship between the two variables — in this case, electric vehicle demand and the price of gasoline. Figure 6-5 shows a sample relationship between the price of gasoline and the demand for electric cars.
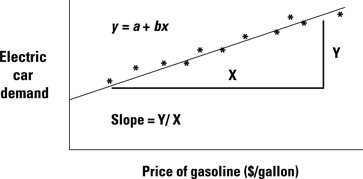
Illustration by Wiley, Composition Services Graphics
Figure 6-5: Causal relationship.
By plotting the variables, you can derive an equation that shows their relationship. The value of the second (or dependent) variable (y) is given by the following equation:
Y = a + bx
x is the value of the first (or independent variable), b is the slope of the line (the change in the y value divided by the change in the x value), and a is the value of y when x is 0.
For example, assume a is 40,000 cars and b is 10,000 cars per $1.00 increase in gasoline prices. If the price of gas (x) is $4.50, then the forecast for car sales is 40,000 + (10,000)(4.50) = 85,000 cars.
Acknowledging the Error of Your Ways
Forecasts tend to be inaccurate, and you need to find out how (in)accurate your forecasting model is. Forecasting error is the difference between the forecast and actual values. In this section, we point out the most common reasons that forecasts are inaccurate and give you metrics for determining how off target you are.
Hunting down the source of your error
Forecasts are inaccurate for many reasons. Here are some of the most common sources of errors:
 Incorrectly identifying the relationship between variables: In the Identifying related variables section earlier in the chapter, we give you a formula to identify the correlation between one variable and another. In reality, there may be more than one variable determining an outcome. For example, sales of electric automobiles can be related to not only the price of gasoline but also the price of the car itself and the availability of public charging stations in your town. Multivariate analysis is outside the scope of this book, but you should be aware that correctly identifying variables has an impact on your forecast.
Incorrectly identifying the relationship between variables: In the Identifying related variables section earlier in the chapter, we give you a formula to identify the correlation between one variable and another. In reality, there may be more than one variable determining an outcome. For example, sales of electric automobiles can be related to not only the price of gasoline but also the price of the car itself and the availability of public charging stations in your town. Multivariate analysis is outside the scope of this book, but you should be aware that correctly identifying variables has an impact on your forecast.
 Not recognizing trends in demand: When you fail to recognize trends (either upward or downward) and don’t account for them in your forecasting model, your forecast will significantly lag your actual demand. Trends can change quickly and be subtle and therefore be difficult to observe. Using the wrong trend line is a common mistake.
Not recognizing trends in demand: When you fail to recognize trends (either upward or downward) and don’t account for them in your forecasting model, your forecast will significantly lag your actual demand. Trends can change quickly and be subtle and therefore be difficult to observe. Using the wrong trend line is a common mistake.
 Not updating forecasting assumptions and techniques: You should monitor your forecasting method on a regular basis to detect any changes in demand patterns. Fundamental shifts in demand may require you to change your forecasting technique. By monitoring your forecasting error, you can quickly detect changes in your demand.
Not updating forecasting assumptions and techniques: You should monitor your forecasting method on a regular basis to detect any changes in demand patterns. Fundamental shifts in demand may require you to change your forecasting technique. By monitoring your forecasting error, you can quickly detect changes in your demand.

 Projecting past trends into the future: When you use the time-series methods (moving average and exponential smoothing), you’re making the assumption that past patterns will continue in the future. This can be dangerous, especially in rapidly changing markets, where products experience tremendous growth in demand or become obsolete quickly. For information on product life cycles, check out Chapter 18.
Projecting past trends into the future: When you use the time-series methods (moving average and exponential smoothing), you’re making the assumption that past patterns will continue in the future. This can be dangerous, especially in rapidly changing markets, where products experience tremendous growth in demand or become obsolete quickly. For information on product life cycles, check out Chapter 18.
 Reacting to random or special cause variations: Random variation is the natural shifts that occur from many minor sources. It’s the “noise” in your system that can’t be explained. Special cause variation is fluctuation that can be contributed to an event that doesn’t normally occur, such as a hurricane warning that forces evacuations and causes a rise in hotel stays in certain areas. Don’t react to these variations, because they’re unpredictable and nonrecurring. For more on the statistical nature of random variations, see Chapter 12.
Reacting to random or special cause variations: Random variation is the natural shifts that occur from many minor sources. It’s the “noise” in your system that can’t be explained. Special cause variation is fluctuation that can be contributed to an event that doesn’t normally occur, such as a hurricane warning that forces evacuations and causes a rise in hotel stays in certain areas. Don’t react to these variations, because they’re unpredictable and nonrecurring. For more on the statistical nature of random variations, see Chapter 12.
 Relying on biased information sources: Sales performance is often measured based on actual sales as compared to the forecast. If actual sales exceed the forecast, salespeople are often rewarded, so low forecasts offer them a greater chance of exceeding it. Production staff, on the other hand, tend to prefer high demand forecasts so they have more resources available to meet the forecasted demand. Be sure to consider the source of information for your forecasts. Avoid or minimize bias to create accurate forecasts.
Relying on biased information sources: Sales performance is often measured based on actual sales as compared to the forecast. If actual sales exceed the forecast, salespeople are often rewarded, so low forecasts offer them a greater chance of exceeding it. Production staff, on the other hand, tend to prefer high demand forecasts so they have more resources available to meet the forecasted demand. Be sure to consider the source of information for your forecasts. Avoid or minimize bias to create accurate forecasts.
 Using an insufficient number of data points: Using time-series data often requires a significant amount of data, especially if trends or seasonality conditions exist. What may look like a pattern in your data may actually be random variation in demand. Accurately identifying seasonal shifts in demand requires a significant amount of past data. You want to make sure you have enough points to observe the pattern over several seasons. Exactly how much past data you need depends on the nature of your business and product. Choosing the number you need requires statistical analysis beyond the scope of this book.
Using an insufficient number of data points: Using time-series data often requires a significant amount of data, especially if trends or seasonality conditions exist. What may look like a pattern in your data may actually be random variation in demand. Accurately identifying seasonal shifts in demand requires a significant amount of past data. You want to make sure you have enough points to observe the pattern over several seasons. Exactly how much past data you need depends on the nature of your business and product. Choosing the number you need requires statistical analysis beyond the scope of this book.
Measuring how inaccurate you are
A company makes many important decisions based on what it anticipates future demand to be. These decisions include how much capacity to purchase and maintain, how many people to hire, and how much inventory to hold. Making these decisions on an inaccurate forecast can be very costly to the bottom line. If the forecast overestimates demand, the firm can spend money on unnecessary capacity and can end up with an excess of inventory that it can’t sell. On the other hand, if the forecast underestimates demand, the company may find a growing backlog of orders or, worse yet, it may lose sales because of the unavailability of products. Because of the high stakes involved, it’s important to monitor the accuracy of the forecast.
You have a few different options for measuring how inaccurate your forecast is. This section describes some of these methods and points out when you should think about changing your forecasting model. The first two methods measure the average error of the forecast in terms of the demand being forecast. The second pair measures the error in percentage terms, which is probably more important to the typical user of forecasts. Finally, we describe a way for you to determine if any systematic bias exists in your forecast.
Mean absolute deviation (MAD) and mean squared error (MSE)
One of the most common ways to assess the mean absolute error is to find the mean absolute deviation (MAD) with this formula:

In this equation, you average the absolute value of the error over n periods.
Mean squared error (MSE) is the average squared error and is calculated as

Here, the error is squared.
The difference between these two measurements is that MAD weights all errors evenly, and MSE weights the errors by their squared values. Because of this squaring, MSE is more sensitive (gives more weight) to outliers, and the units are the square of the variable’s units, which is often confusing to interpret.
The primary use of these measures is to allow you to compare different forecasting methods. For example, you could forecast using exponential smoothing and compare the errors for different values of α, choosing the one that results in the lowest value of MAD or MSE.
Mean absolute percent error (MAPE)
One significant issue with MAD and MSE is that they produce a result in absolute terms, meaning that a product with greater demand gives a larger measure than a product with less demand. Mean absolute percent error (MAPE) takes care of this by providing the error in percentage terms. You calculate MAPE using this equation:
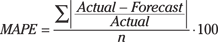
Tracking signal (TS)
Because of inevitable changes in demand patterns, it’s necessary to have a way to tell when your current forecasting method is no longer working. One option is to use control charts that monitor your error over time; another option is to use a tracking signal (TS). (Check out Chapters 12 and 13 for details on how to make and use a control chart.)
Here’s the equation for the tracking signal:

The TS shows bias that may exist in your forecast. Bias is the tendency for the forecast to always be greater or less than the actual value of the demand. If the TS exceeds a predetermined value, you want to consider changing your forecasting model.
 Forecasting demand — not sales — is the name of the game. If you forecast future sales based on past sales, you may miss significant demand for your product. Sales data doesn’t account for the fact that some potential customers may not have been able to purchase your product in the past because it wasn’t available. It also doesn’t account for a changing market size.
Forecasting demand — not sales — is the name of the game. If you forecast future sales based on past sales, you may miss significant demand for your product. Sales data doesn’t account for the fact that some potential customers may not have been able to purchase your product in the past because it wasn’t available. It also doesn’t account for a changing market size. In general, you want to choose a small
In general, you want to choose a small