As you prepare for the SAT Subject Test: Physics, you might need to review some of your graphing skills. You will need to be able to interpret linear and parabolic graphs, and find the slope of a line and the area under a curve.
A linear graph results when we plot two quantities that are proportional to each other. The change in the quantity on the y-axis is called the rise, and the change in the quantity on the x-axis is called the run. The rise divided by the run is a constant for a linear graph, and we call this constant the slope, denoted by the letter m. We write:
The slope of a linear graph is defined as the rate of change of y with respect to x.
Example: A simple circuit consisting of a power supply, wires of negligible resistance, and a resistor is connected, and several voltages and currents are measured. A graph of voltage (in volts) versus current (in amperes) for a simple circuit is plotted on the following page.
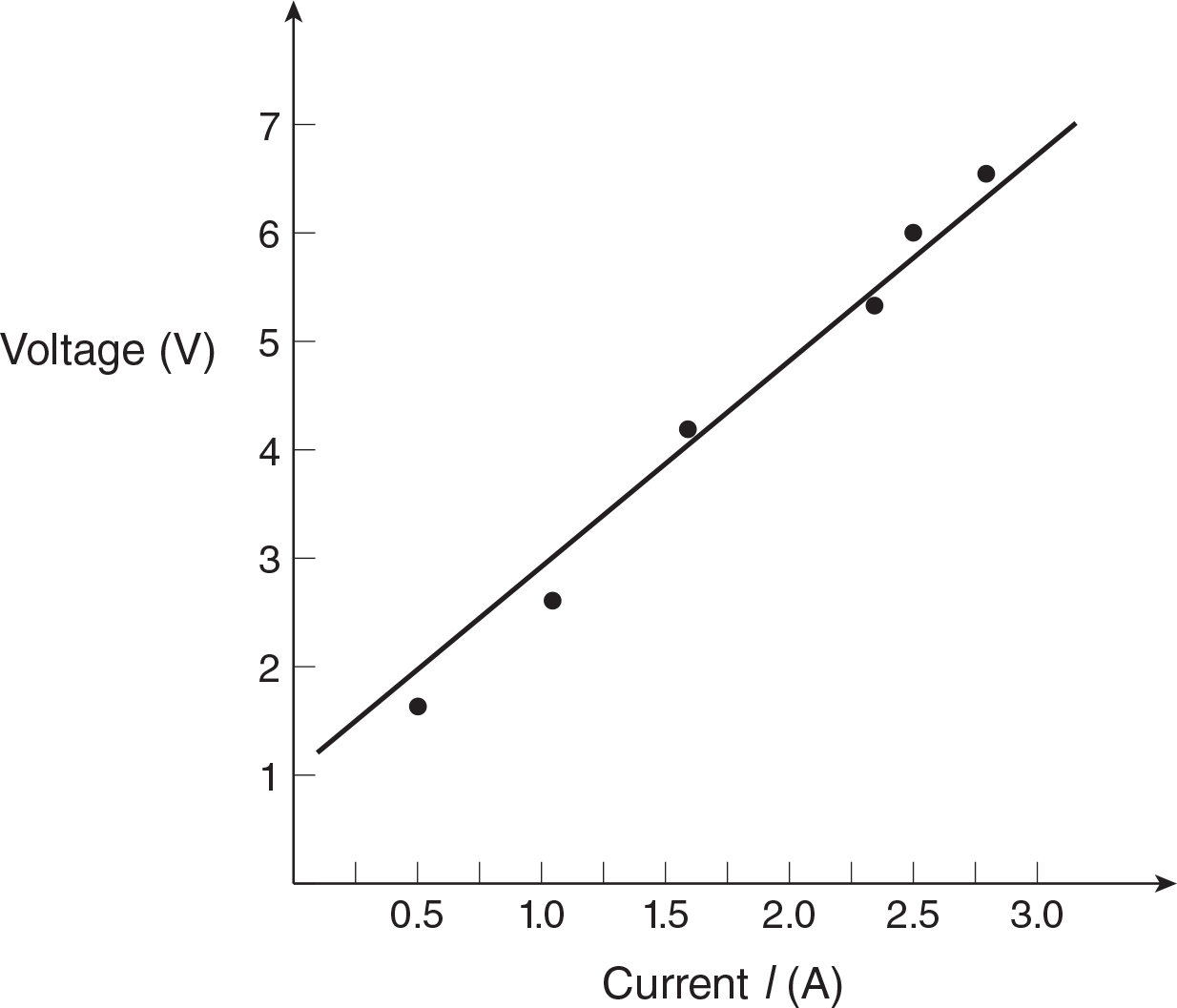
We see that we can draw the best-fit straight line through the data points. Remember, a best-fit line represents the average of the data, so points should be distributed evenly both above and below the line. The slope of the line can be found by choosing two points that are on the line. In this case, we have chosen the points (0.5 A, 2 V) and (2.5 A, 6 V):
The ratio of the voltage to the current is the resistance of the circuit. We say that voltage and current are proportional to each other, and the resistance is the slope of a voltage vs. current graph. We will return to circuits in chapter 12.
Another common way to analyze a graph is to find the area under the curve. Remember, a curve is a generic word for any line resulting from graphing two quantities, and can mean a curved line or a straight line. The area under a curve is equal to the product of the two quantities on the axes for a particular interval. For example, consider the graph of velocity (in meters per second) vs. time (in seconds) on the following page.
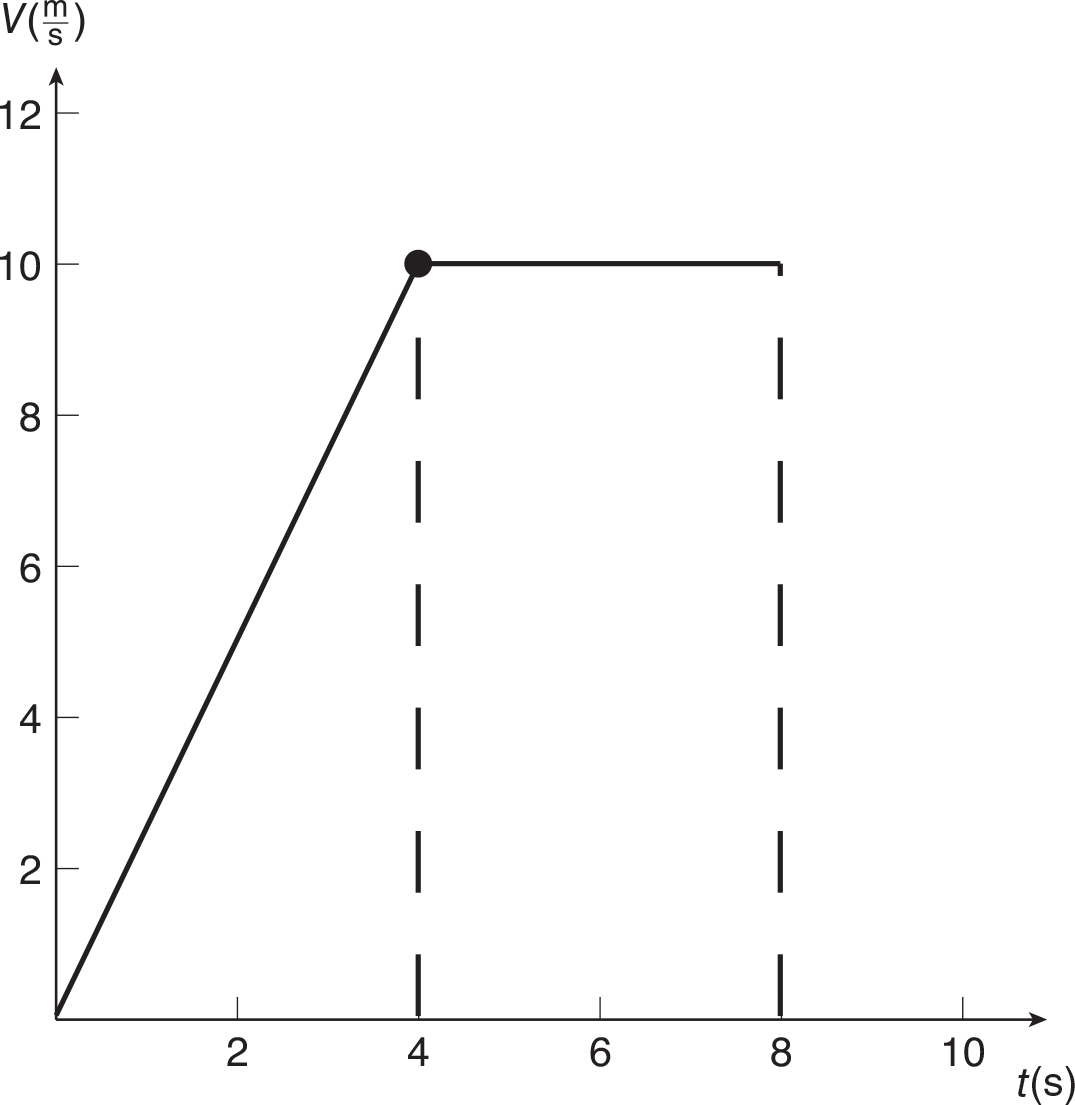
If we consider the time interval from 0 to 8 s, we can find the area under the curve (graph). The area from 0 to 4 s is the area of a triangle with a base of 4 s and a height of 10 m/s. The area from 4 s to 8 s is a rectangle with a base of 4 s and a height of 10 m/s. The total area under the graph is the sum of the area of the triangle and the area of the rectangle:
Note that the units for the area under the graph is meters, which indicates that the area under a velocity vs. time graph is displacement. Motion is discussed further in chapter 4.
Often, two quantities in physics are not proportional to each other, but one quantity depends on the square of the other. For example, for an object falling freely from rest, the total distance fallen is proportional to the square of the time it has been falling. The equation that relates distance fallen to the time of fall is
where g is the acceleration of the falling object due to gravity, about 10 m/s2. Since s is proportional to t2 (and not to t), the graph of s vs. t will be a parabola.
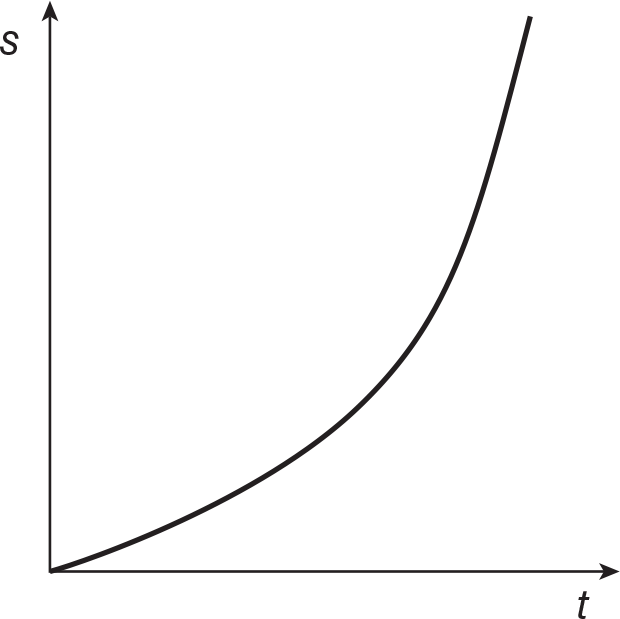
Of course, if we plotted s vs. t2, we would get a straight line with a slope of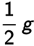 
. We will review several examples of parabolic relationships in later chapters.
