WHEN WE TALK of physics as patterns of organic energy, the word that catches our attention is “organic”. Organic means living. Most people think that physics is about things that are not living, such as pendulums and billiard balls. This is a common point of view, even among physicists, but it is not as evident as it may seem.
Let us explore this viewpoint with the aid of a hypothetical person, a young man named Jim de Wit who is the perpetual champion of the non-obvious.
“It is not at all true,” says Jim de Wit, “that physics is about nonliving things. This is evident from our discussion of falling bodies (see here). Even if some of them are the human kind, they all accelerate at the same rate in a vacuum. So physics does apply to living things.”
“But that is an unfair example,” we say. “Rocks have no choice in the matter of falling. If we drop them, they fall. If we don’t drop them, they don’t fall. Humans, on the other hand, exercise choice. Accidents excluded, humans ordinarily are not found in the act of falling. Why? Because they know that falling may hurt them and they have no desire to be hurt. In other words, humans process information (they know that they may be hurt) and they respond to it (by not falling). Rocks can do neither.”
“That is the way things appear,” says de Wit, “but it may not be the way they actually are. For example, by watching time-lapse photography we know that plants often respond to stimulae with human-like reactions. They retreat from pain, advance toward pleasure, and even languish in the absence of affection. The only difference is that they do it at a much slower rate than we do. So much slower, in fact, that it appears to the ordinary perception that they do not react at all.
“If this is so, then how can we say with certainty that rocks, and even mountain ranges, do not react also as living organisms, but with a reaction time so slow that to catch it with time-lapse photography would require millennia between exposures! Of course, there is no way to prove this, but there is no way of disproving it either. The distinction between living and nonliving is not so easy to make.”
“That’s clever,” we think, “but from a practical point of view, it cannot be observed that inert matter responds to stimulae, and there is no question that humans do.”
“Wrong again!” says de Wit, reading our thoughts. “Any chemist can verify that most chemicals (which usually come out of the ground as rocks) do react to stimulation. Under the right conditions, for example, sodium reacts to chlorine (by forming sodium chloride—salt), iron reacts to oxygen (by forming iron oxides—rust), and so on, just as humans react to food when they are hungry and to affection when they are lonely.”
“Well, this is so,” we admit, “but it hardly seems fair to compare a chemical reaction to a human reaction. A chemical reaction either happens or it does not happen. There is nothing in between. When two such chemicals are combined properly, they react; if they are not properly combined, they do not react. Humans are much more complex.
“If we offer food to a hungry person, he might eat it or he might not, depending upon his circumstances; and if he eats, he might eat his fill or he might not. Consider the person who is hungry and late for an appointment. If the appointment is important enough, he will go without eating, even though he is hungry. If a person knows that his food is poisonous, he will not eat, even though he is hungry. It is a matter of processing information and responding appropriately that distinguishes a human reaction from a chemical reaction. Chemicals have no options; they always must act one way or the other.”
“Of course,” beams Jim de Wit, “but how do we know that our responses are not as rigidly preprogrammed as those of a chemical, with the only difference being that our programs are enormously more complex? We may not have any more freedom of action than stones do, although, unlike stones, we deceive ourselves into thinking that we do!”
We have no way to dispute this argument. De Wit has shown us the arbitrary quality of our prejudices. We would like to think that we are different from stones because we are living and they are not, but there is no way we can prove our position or disprove his. We cannot establish clearly that we are different from inorganic substances. That means that, logically, we must admit that we may not be alive. Since this is absurd, the only alternative is to admit that “inanimate” objects may be living.
The distinction between organic and inorganic is a conceptual prejudice. It becomes even harder to maintain as we advance into quantum mechanics. Something is organic, according to our definition, if it can respond to processed information. The astounding discovery awaiting newcomers to physics is that the evidence gathered in the development of quantum mechanics indicates that subatomic “particles” constantly appear to be making decisions! More than that, the decisions they seem to make are based on decisions made elsewhere. Subatomic particles seem to know instantaneously what decisions are made elsewhere, and elsewhere can be as far away as another galaxy! The key word is instantaneously. How can a subatomic particle over here know what decision another particle over there has made at the same time the particle over there makes it? All the evidence belies the fact that quantum particles are actually particles.
A particle, as we mentally picture it (classically defined) is a thing which is confined to a region in space. It is not spread out. It is either here or it is there, but it cannot be both here and there at the same time.
A particle over here can communicate with a particle over there (by shouting at it, sending it a TV picture, waving, etc.), but that takes time, even if only milliseconds. If the two particles are in different galaxies, it could take centuries. For a particle here to know what is going on over there while it is happening, it must be over there. But if it is over there, it cannot be here. If it is both places at once, then it is no longer a particle.
This means that “particles” may not be particles at all (see here). It also means that these apparent particles are related with other particles in a dynamic and intimate way that coincides with our definition of organic.
Some biologists believe that a single plant cell carries within it the capability to reproduce the entire plant. Similarly, the philosophical implication of quantum mechanics is that all of the things in our universe (including us) that appear to exist independently are actually parts of one all-encompassing organic pattern, and that no parts of that pattern are ever really separate from it or from each other.
To understand these decisions and what makes them, let us start with a discovery made in 1900 by Max Planck. This year generally is considered the birthday of quantum mechanics. In December of that year, Planck reluctantly presented to the scientific community a paper which was to make him famous. He himself was displeased with the implications of his paper, and he hoped that his colleagues could do what he could not do: explain its contents in terms of Newtonian physics. He knew in his heart, however, that they could not, and that neither could anyone else. He also sensed, and correctly so, that his paper would shift the very foundations of science.
What had Planck discovered that disturbed him so much? Planck had discovered that the basic structure of nature is granular, or, as physicists like to say, discontinuous.
What is meant by “discontinuous”?
If we talk about the population of a city, it is evident that it can fluctuate only by a whole number of people. The least the population of a city can increase or decrease is by one person. It cannot increase by .7 of a person. It can increase or decrease by fifteen people, but not by 15.27 people. In the dialect of physics, a population can change only in discrete increments, or discontinuously. It can get larger or smaller only in jumps, and the smallest jump that it can make is a whole person. In general, this is what Planck discovered about the processes of nature.
Planck did not intend to undermine the foundations of Newtonian physics. He was a conservative German physicist. Rather, he inadvertently fathered the revolution of quantum mechanics by attempting to solve a specific problem dealing with energy radiation.
Planck was searching for an explanation of why things behave as they do when they get hot. Namely, he wanted to know how objects glow brighter as they get hotter, and change color when the temperature is increased or decreased.
Classical physics, which successfully had unified such diverse fields as acoustics, optics, and astronomy, which had all but satiated the scientific appetite, which had unraveled the enigmas of the universe and rearranged them in neat packages, held no sensible explanation of this commonplace phenomenon. It was, to use the parlance of the day, one of the few “clouds” on the horizon of classical physics.
In 1900 physicists pictured the atom as a nucleus that looked something like a plum to which were attached tiny protruding springs. (This was before the planetary model of the atom). At the end of each spring was an electron. Giving the atom a jolt, by heating it, for instance, caused its electrons to jiggle (oscillate) on the ends of their springs. The jiggling electrons were thought to give off radiant energy, and this was thought to account for the fact that hot objects glow. (An accelerating electrical charge creates electromagnetic radiation). (An electron carries an electrical charge (negative) and if it is jiggling, it is accelerating—first in one direction and then in the other).
Physicists thought that heating the atoms in a metal caused them to become agitated, and this in turn caused their electrons to jiggle up and down and emit light in the process. The energy that the atom absorbed when it was jolted (heated), the theory went, was radiated by the jiggling electrons. (You can substitute “atomic oscillators” if your friends won’t take “jiggling electrons” seriously).
This same theory also claimed that the energy absorbed by an atom was distributed equally to its oscillators (electrons) and that those electrons which oscillated (jiggled) at higher frequencies (faster) radiated their energy most efficiently.
Unfortunately, this theory didn’t work. It “proved” some very incorrect things. First, it “proved” that all heated objects emit more high-frequency light (blue, violet) than low-frequency light (red). In other words, even moderately hot objects, according to this classical theory, emit an intense blue-white color, just like objects which are white-hot, but in lesser amounts. This is incorrect. Moderately hot objects emit primarily red light. Second, the classical theory “proved” that highly heated objects radiate infinite amounts of high-frequency light. This is incorrect. Highly heated objects emit a finite amount of high-frequency light.
Do not be concerned with high frequencies and low frequencies. These terms will be explained shortly. The point is that Planck was exploring one of the last major problems of classical physics: its erroneous predictions concerning energy radiation. Physicists dubbed this problem “The Ultra-Violet Catastrophe”. This tongue in cheek description reflected a real concern with the fact that heated objects do not radiate large amounts of energy in the form of ultraviolet light (the highest-frequency light known in 1900) the way the classical theory predicted.
The name of the phenomenon that Planck was studying is black-body radiation. Black-body radiation is the radiation that comes from a nonreflecting, perfectly absorbing, flat (nonglossy) black body. Since black is the absence of color (no light is reflected or emitted), black bodies have no color unless we heat them. If a black body is glowing a certain color, we know that it is because of the energy that we have added to it and not because it reflects or emits that color spontaneously.
A “black body” does not always mean a solid body that is black. Suppose that we have a metal box that is completely sealed except for a small hole. If we look inside, what do we see? Nothing, because there is no light in there. (A little light may come in through the hole, but not that much).
Now suppose that we heat the box until it glows red and then look through the hole. What do we see? Red (of course). This is the kind of phenomenon that Planck studied.
All the physicists in 1900 assumed that after the electrons of an excited atom began to jiggle, they radiated their energy smoothly and continuously until they “ran down” and their energy was dissipated. Planck discovered that excited atomic oscillators do not do this. They emit and absorb energy only in specific amounts! Instead of radiating energy smoothly and continuously like a clock spring runs down, they radiate their energy in spurts, dropping to a lower energy level after each spurt until they stop oscillating altogether. In short, Planck discovered that the changes of nature are “explosive”, not continuous and smooth.fn1
Planck was the first physicist to talk about “energy packets” and “quantized oscillators”. He sensed that he had made a major discovery, one which ranked with the discoveries of Newton, and he was right. The philosophy and paradigms of physics never were to be the same, although it took another twenty-seven years for “quantum mechanics” to take form.
It is difficult today to understand how bold was Planck’s theory of quanta. Victor Guillemin, professor of physics at Harvard, put it this way:
[Planck] had to make a radical and seemingly absurd assumption, for according to classical laws, and common sense as well, it had been presumed that an electronic oscillator, once set in motion by a jolt, radiates its energy smoothly and gradually while its oscillatory motion subsides to rest. Planck had to assume that the oscillator ejects its radiation in sudden spurts, dropping to lesser amplitudes of oscillation with each spurt. He had to postulate that the energy of motion of each oscillator can neither build up nor subside smoothly and gradually but may change only in sudden jumps. In a situation where energy is being transferred to and fro between the oscillators and the light waves, the oscillators must not only emit but also absorb radiant energy in discrete “packets”. . . . He coined the name “quanta” for the packets of energy, and he spoke of the oscillators as being “quantized”. Thus, the trenchant concept of the quantum entered physical science.1
Planck is not only the father of quantum mechanics, he also is the discoverer of Planck’s constant. Planck’s constant is a certain number which never changes.fn2 It is used to calculate the size of the energy packets (quanta) of each light frequency (color). (The energy in each light quantum of a particular color is the frequency of the light multiplied by Planck’s constant).
All of the energy packets of each color have the same amount of energy. All of the energy packets of red light, for example, are the same size. All of the energy packets of green light are the same size. All of the energy packets of violet light are the same size. The energy packets of violet light, however, are larger than the energy packets of green light, and the energy packets of green light are larger than the energy packets of red light.
In other words, Planck discovered that energy is absorbed and emitted in little chunks and that the size of the chunks of a low-frequency light, like red, is smaller than the size of the chunks of a high-frequency light, like violet. This explains why hot objects radiate energy as they do.
When a black body is put over low heat, the first color it glows is red because the energy packets of red light are the smallest energy packets in the visible light spectrum. As the heat is increased, more energy is available to shake loose bigger energy packets. The bigger energy packets make the higher-frequency colors, such as blue and violet.
Why does the glow of hot metal seem to increase steadily in brightness as the temperature increases? Because the tiny “steps” upward and downward in brightness are so incredibly small that our eyes cannot discern them. Therefore, on the large scale, or macroscopic level, this aspect of nature is not evident. In the subatomic realm, however, it is the dominant characteristic of nature.
If this discussion of emission and absorption of energy packets reminds you of Niels Bohr (see here), you are right. However, Bohr was not to arrive at his theory of specific electron orbits for another thirteen years. By that time physicists had discarded the plum-with-jiggling-electrons model of the atom in favor of the planetary model, in which electrons revolve around a nucleus.fn3
Between Planck’s discovery of the quantum (1900) and Bohr’s analysis of the hydrogen spectrum (1913), a brilliant physicist burst upon the scene with a force seldom exerted by an individual. His name was Albert Einstein. In one year (1905), at twenty-six, Einstein published five significant papers. Three of them were pivotal in the development of physics, and, to a large extent, in the development of the West. The first of these three papers described the quantum nature of light. It won him a Nobel Prize in 1921. The second paper described molecular motion. The third paper set forth the special theory of relativity, which we will study later.fn4
Einstein’s theory of light was that it is composed of tiny particles. A beam of light, said Einstein, is analogous to a stream of bullets. Each bullet is called a photon. This is similar to what Planck proposed, but actually it is a leap beyond. Planck discovered that energy is absorbed and emitted in packets. He described the processes of energy absorbtion and emission. Einstein theorized that energy itself is quantized.
To prove his theory, Einstein referred to a phenomenon called the photoelectric effect. When light hits (impinges on) the surface of a metal, it jars electrons loose from the atoms in the metal and sends them flying off. With appropriate equipment, we can count these electrons and measure how fast they are traveling.
Einstein’s theory of the photoelectric effect was that each time one of the bullets, or photons, hits an electron, it knocks it away just as one billiard ball hitting another billiard ball knocks it away.
Einstein based his revolutionary theory on the experimental work of Philippe Lenard (who won the Nobel Prize in 1905). Lenard showed that the flow of electrons in the photoelectric effect begins immediately when the impinging light strikes the target metal. Turn on the light and out come the electrons. According to the wave theory of light, the electrons in a metal only start to jiggle when they are struck by light waves. They do not come out of the metal until they are moving fast enough. This takes several oscillations, like pumping a child’s swing higher and higher until it goes around the bar. In short, the wave theory of light predicts a delayed emission of electrons. Lenard’s experiments showed a prompt emission of electrons.
This prompt emission of electrons in the photoelectric effect is explained by Einstein’s particle theory of light. Every time a particle of light, a photon, strikes an electron, it immediately knocks it out of its atom.
Lenard also discovered that reducing the intensity of the impinging light beam (making it dimmer) did not reduce the velocity of the rebounding electrons, but it did reduce the number of the rebounding electrons. He found that the velocity of the rebounding electrons could be altered, however, by changing the color of the impinging light.
This also was explained by Einstein’s new theory. According to Einstein’s theory, each photon of a given color, like green, for instance, has a certain amount of energy. Reducing the intensity of a beam of green light only reduces the number of photons in the beam. Each remaining photon, however, still has the same amount of energy as any other photon of green light. Therefore, when any photon of green light strikes an electron, it knocks it away with a certain amount of energy which is characteristic of green-light photons.
Max Planck described Einstein’s theory this way:
. . . The photons (the “drops” of energy) do not grow smaller as the energy of the ray grows less; what happens is that their magnitude remains unchanged and they follow each other at greater intervals.2
Einstein’s theory also substantiated Planck’s revolutionary discovery. High-frequency light, like violet, is made of higher-energy photons than low-frequency light, like red. Therefore, when violet light, which is made of high-energy photons, strikes an electron, it causes the electron to rebound with a high velocity. When red light, which is made of low-energy photons, strikes an electron, it causes the electron to rebound at a low velocity. In either case, increasing or decreasing the intensity of the light increases or decreases the number of rebounding electrons, but only by changing the color of the impinging light can we change their velocity.
In short, Einstein demonstrated, using the photoelectric effect, that light is made of particles, or photons, and that the photons of high-frequency light have more energy than the photons of low-frequency light. This was a momentous achievement. The only problem was that one hundred and two years earlier an Englishman named Thomas Young had shown that light is made of waves, and no one, including Einstein, was able to disprove him.
Now we come to the matter of waves. A particle is something that is contained in one place. A wave is something that is spread out. Below are some types of waves.

We are concerned only with the last type of wave. Here is a more detailed picture of it.
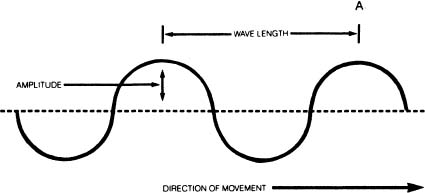
A wavelength is the distance between one crest of a wave and the next. The longest radio waves are over six miles long. X-rays, on the other hand, are only about one billionth of a centimeter long. Visible light has wavelengths in the neighborhood of four to eight one hundred thousandths of a centimeter.
The amplitude of a wave is the height of the wave crest above the dotted line. Here are three waves with different amplitudes. The one in the middle has the largest amplitude.
The frequency of the wave tells us how many crests pass a given point (like point A in the drawing at the top of the page) each second. If the wave is moving in the direction of the arrow and a crest passes point A each second, the frequency of the wave is one cycle per second. If ten and one half crests pass point A every second, the frequency of the wave is 10.5 cycles per second. If ten thousand crests pass the same point every second, the frequency of the wave is 10,000 cycles per second, and so on.
The velocity of the wave can be determined by multiplying the wavelength by the frequency. For example, if the wavelength of a wave is two feet and the frequency of the wave is one cycle per second, the wave is moving one wavelength (two feet) every second. Therefore, its velocity is two feet per second. If the wavelength is two feet and the frequency is three cycles per second, the velocity of the wave is six feet per second because the wave moves three wavelengths forward every second.
There is nothing complicated about this. We can determine how fast a man is running if we know the length of his stride and how many of them he takes in a second. By multiplying them together we get how far the man runs in a second. If his stride is three feet and he takes two strides per second, then he runs six feet per second (about four miles per hour). We do the same things with waves, except that we use wavelengths instead of strides.
Although the velocity of a light wave can be determined by multiplying its wavelength by its frequency, it is not necessary. Physicists have discovered that the velocity of light in empty space is always 186,000 miles per second. This applies to all electromagnetic waves, including light. Therefore, all light waves (blue ones, green ones, red ones, etc.) have the same velocity as radio waves, x-rays, and all the other forms of electromagnetic radiation. The speed of light is a constant. It is represented by the letter “c”.
The constant “c” is (approximately) 186,000 miles per second and it never varies (which is what makes it a “constant”). It does not matter whether light is going up or down, has a high frequency or a low frequency, a large wavelength or a small wavelength, is coming toward us or going away from us: Its velocity is always 186,000 miles per second. This fact led Albert Einstein to the theory of special relativity, as we shall see later.
It also permits us to know both the frequency and the wavelength of light if we know either one of them. This is because the product of the two is always 186,000 miles per second in empty space. The larger one of them is, the smaller the other must be. For example, if we know that by multiplying two numbers together we get 12 for an answer, and if we know that one of the numbers is 6, then we also know that the other number must be 2. If we know that one of the numbers is 3, then we know that the other number must be 4.
Similarly, the higher the frequency of a light wave, the shorter its wavelength must be; the lower the frequency of a light wave, the longer its wavelength must be. In other words, high-frequency light has a short wavelength and low-frequency light has a long wavelength.
Now we return to Planck’s discovery. Planck discovered that the energy of a light quantum increases with frequency. The higher the frequency, the higher the energy. Energy is proportional to frequency, and Planck’s constant is the “constant of proportionality” between them. This simple relation between frequency and energy is important. It is central to quantum mechanics. The higher the frequency, the higher the energy; the lower the frequency, the lower the energy.
When we put wave mechanics and Planck’s discovery together we get this: High-frequency light, such as violet light, has a short wavelength and high energy; low-frequency light, such as red light, has a long wavelength and low energy.
This explains the photoelectric effect. Photons of violet light knock electrons loose from the atoms of a metal and send them flying away at a higher velocity than photons of red light because the photons of violet light, which is a high-frequency light, have more energy than the photons of red light, which is a low-frequency light.
This all makes sense if you overlook the fact that we are talking about particles (photons) in terms of waves (frequencies) and waves in terms of particles, which, of course, makes no sense at all.
If you feel that you understand the last few pages, congratulations! You have mastered the most difficult mathematics in the book. If not, go back here and reread these pages. It is easy to dance with wavelengths and frequencies if you know how they are connected.
Waves are playful creatures that like to do dances of their own. For example, under certain conditions they bend around corners. When this happens it is called diffraction.
Imagine that we are in a helicopter hovering over the mouth of an artificial harbor. The mouth of the harbor is wide enough for two aircraft carriers to pass each other going through it. The sea is rough and the wind and waves are blowing straight into the mouth of the harbor. When we look down, this is the pattern that we see the waves making in the harbor:
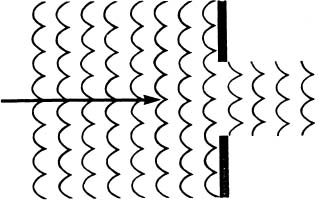
The waves are stopped cleanly by the walls of the harbor except at the harbor entrance, where they continue straight forward into the harbor until they are dissipated.
Now imagine that the mouth of the harbor is so small that a row-boat scarcely can pass through it. As we look down from the helicopter, the pattern we see is quite different.
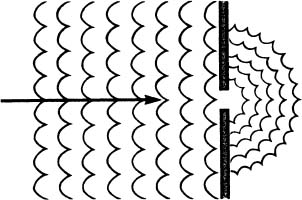
Instead of moving directly ahead into the harbor, the waves inside the harbor are spreading out from the mouth of the harbor almost as if it were a pond and we had dropped a rock into it at that point. This is diffraction.
Why does it happen? Why does reducing the size of the harbor mouth cause the wave pattern inside the harbor to spread out in semicircles?
The answer lies in comparing the size of the harbor mouth to the size of the wavelength of the incoming waves. In the first case, the size of the harbor mouth is considerably larger than the distance between the crests of the waves going through it, and the waves proceed directly through it into the harbor following a straight line (rectilinear propagation) as waves usually do.
In the second case, the size of the harbor mouth is about the same size, or smaller, than the wavelength of the incoming waves, and when this happens, it causes the characteristic pattern (diffraction) that we see in the drawing.
Whenever waves pass through an opening that is so small that the wavelength of the waves passing through it seems large in comparison, the waves passing through it diffract.
Since light is a wave phenomenon (according to the wave theory of light), it should behave in the same way, and it does. If we place a light source behind a cut-out like the one below, it casts a projection on the wall like this one:
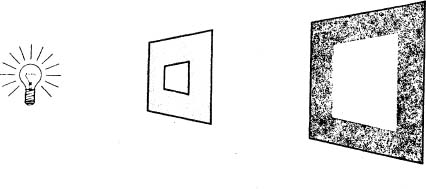
This is analogous to sea waves entering the large harbor mouth. The width of the cut-out is millions of times larger than the wavelength of the light. As a result, the light waves go straight through it, following straight lines and projecting onto the wall a figure with the same shape as the cut-out. Notice especially that this projection has distinct borders between the bright area and the dark area.
If we make the cut-out no larger than a razor slit so that its width is roughly as small as the wavelength of the incoming light, the light diffracts. Now the sharp boundary between the light area and the dark area disappears and we see a bright area that fades into darkness at the edges. Instead of proceeding in a straight line to the wall, the light beam has spread out like a fan. This is diffracted light.
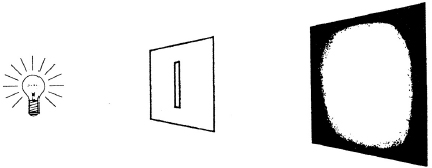
Now that you know what happens, here is the story.
In 1803, Thomas Young settled once and for all (he thought) the question of the nature of light. He used an experiment that was both simple and dramatic. In front of a light source (Young used sunlight coming through a hole in a screen) he placed a screen with two vertical slits in it. Each slit could be covered over with a piece of material.
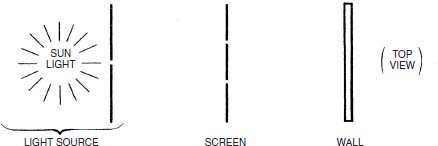
On the other side of the double-slit screen was a wall against which the light coming through the double slits could shine. When the light source was turned on and one of the slits was covered up, the wall was illuminated like the first drawing on the next page.
When both slits were uncovered, however, Young made history. The projection on the wall should have been the sum of the light from the two slits, but it wasn’t. Instead, the wall was illuminated with alternating bands of light and darkness! The center band was the brightest. On both sides of the center band of light were bands of darkness; then bands of light, but less intense than the center band; then bands of darkness, etc., as below.

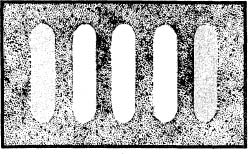
The simplicity of the answer is what makes this experiment a great one. The alternating light and dark bands are a well-known phenomenon of wave mechanics called interference. Interference results when the waves of light diffracting from the two slits interfere with each other. In some places these waves overlap and reinforce one another. In other places they cancel each other.
In areas where one wave crest overlaps another wave crest, the result is an intensification of light (the light bands). In areas where a crest meets a trough, they cancel each other and no light reaches the wall (the dark bands).
It is just as if we dropped two stones into a pond simultaneously and watched the waves spreading from their points of entry. The waves that the stones make interfere with each other. In places where the crests of the waves caused by one stone meet the crests of the waves caused by the other stone, large waves result. In places where the troughs of the waves caused by one stone meet the crests of the waves caused by the other stone, the water is calm.
In short, Young’s double-slit experiment showed that light must be wave-like because only waves can create interference patterns. The situation, then, was as follows: Einstein, using the photoelectric effect, “proved” that light is particle-like and Young, using the phenomenon of interference, “proved” that light is wave-like. But a wave cannot be a particle and a particle cannot be a wave.
That is just the beginning! Since Einstein “proved” that light is composed of photons, let us go back to Young’s double-slit experiment and run it with photons.fn5 (This has been done). Suppose that we have a light gun which can fire, in effect, one photon at a time. The experiment is set up as before, except that only one slit is open. Now we fire the photon, it goes through the open slit, and we mark where it hits the wall (using a photographic plate). Because we have done this experiment before, we notice that the photon has landed in an area that would be dark if the second slit were open. That is, if the second slit were open, no photons would be recorded in this area.
To make sure, we do the experiment again, but this time we leave both of the slits open. Just as we thought, there are no photons recorded now in the area where the photon hit in our first experiment. When both slits are open and interference is present, this area is in the middle of a dark band.
The question is, How did the photon in the first experiment know that the second slit was not open? Think about it. If both slits are open, there are always alternating bands of illuminated and dark areas. This means that there are always areas where the photons never go (otherwise there would not be any dark areas). If one of the slits is closed, there is no interference and the dark bands disappear; the whole wall becomes illuminated, including those areas which previously were dark when both slits were open.
When we fired our photon and it went through the first slit, how did it “know” that it could go to an area that must be dark if the other slit were open? In other words, how did the photon know that the other slit was closed?
“The central mystery of quantum theory,” wrote Henry Stapp,
is ‘How does information get around so quick?’ How does the particle know that there are two slits? How does the information about what is happening everywhere else get collected to determine what is likely to happen here?3
There is no definitive answer to this question. Some physicists, like E. H. Walker, speculate that photons may be conscious!
Consciousness may be associated with all quantum mechanical processes . . . since everything that occurs is ultimately the result of one or more quantum mechanical events, the universe is “inhabited” by an almost unlimited number of rather discrete conscious, usually nonthinking entities that are responsible for the detailed working of the universe.4
Whether Walker is correct or not, it appears that if there really are photons (and the photoelectric effect “proves” that there are), then it also appears that the photons in the double-slit experiment somehow “know” whether or not both slits are open and that they act accordingly.fn6
This brings us back to where we started: Something is “organic” if it has the ability to process information and to act accordingly. We have little choice but to acknowledge that photons, which are energy, do appear to process information and to act accordingly, and that therefore, strange as it may sound, they seem to be organic. Since we are also organic, there is a possibility that by studying photons (and other energy quanta) we may learn something about us.
The wave-particle duality was the end of the line for classical causality. According to that way of thinking, if we know certain initial conditions, we can predict the future of events because we know the laws that govern them. In double-slit experiments we know all that we can know about initial conditions and we still can’t predict correctly what happens to single photons.
In experiment one, for example (only one slit open), we know the origin of the photon (the lamp), its velocity (186,000 miles per second) and its direction just prior to passing through the open slit. Using Newton’s laws of motion, we can predict where the photon will land on the photographic plate. Let us suppose that we make these calculations.
Now let us consider experiment two (both slits open). Again we know the origin of the photon, its velocity, and its direction just prior to passing through the open slit. The initial conditions of the photon in experiment one are the same as those of the photon in experiment two. They both start from the same place, travel at the same speed, go to the same place, and therefore, are moving in the same direction just prior to passing through slit number one. The only difference is that in the second experiment, the second slit also is open. Again, using Newton’s laws of motion, let us calculate where the photon will land on the photographic plate.
Since we used the same figures and the same formulas in both cases, we get identical answers indicating that the photon in experiment one will impact in exactly the same place as the photon in experiment two. That is the problem. The photon in experiment two will not impact in the same area as the photon in experiment one because the photon in experiment one landed in an area that is a dark band in experiment two. In other words, the two photons do not go to the same place even though the initial conditions pertaining to both of them are identical and known to us.
We cannot determine the paths of individual photons. We can determine what the wave pattern on the wall will be, but in this case we are interested in a single photon, not waves of them. In other words, we know the pattern that large groups of photons will make, and their distribution in the pattern, but we have no way of knowing which photons will go where. All that we can say about a single photon is the probability of finding it in a given place.
The wave-particle duality was (is) one of the thorniest problems in quantum mechanics. Physicists like to have tidy theories which explain everything, and if they are not able to do that, they like to have tidy theories about why they can’t. The wave-particle duality is not a tidy situation. In fact, its untidiness has forced physicists into radical new ways of perceiving physical reality. These new perceptual frames are considerably more compatible with the nature of personal experience than were the old.
For most of us, life is seldom black and white. The wave-particle duality marked the end of the “Either-Or” way of looking at the world. Physicists no longer could accept the proposition that light is either a particle or a wave because they had “proved” to themselves that it was both, depending on how they looked at it.
Of course, Einstein was aware of the fact that his photon theory contradicted Young’s wave theory without disproving it. He speculated that photons were guided by “ghost waves”. Ghost waves were mathematical entities which had no actual existence. The photons seemed to follow paths which had all the mathematical characteristics of waves, but which in reality did not exist. Some physicists still view the wave-particle paradox this way, but for most physicists, this explanation seems too contrived. It is an answer which appears to make sense, but somehow doesn’t explain anything.
The wave-particle duality prompted the first real step in understanding the newly unfolding quantum theory. In 1924, Bohr and two of his colleagues, H. A. Kramers and John Slater, suggested that the waves in question were probability waves. Probability waves were mathematical entities by which physicists could predict the probability of certain events occurring or not occurring. Their mathematics did not prove correct, but their idea, which was unlike anything that had been proposed before, was sound. Later, with a different formalism (mathematical structure), the idea of probability waves developed into one of the distinguishing characteristics of quantum mechanics.
Probability waves, as Bohr, Kramers, and Slater thought of them, was an entirely new idea. Probability itself was not new, but this type of probability was. It referred to what somehow already was happening, but had not yet been actualized. It referred to a tendency to happen, a tendency that in an undefined way existed of itself, even if it never became an event. Probability waves were mathematical catalogues of these tendencies.
This was something quite different from classical probability. If we throw a die in a casino, we know, using classical probability, that the chances of getting the number that we want is one in six. The probability wave of Bohr, Kramers, and Slater meant much more than that.
According to Heisenberg:
It meant a tendency for something. It was a quantitative version of the old concept of “potentia” in Aristotelian philosophy. It introduced something standing in the middle between the idea of an event and the actual event, a strange kind of physical reality just in the middle between possibility and reality.5
By 1924, Planck’s discovery of the quantum was producing seismic effects in physics. It enabled Einstein to discover the photon, which caused the wave-particle duality, which led to probability waves. The physics of Newton was a thing of the past.
Physicists found themselves dealing with energy that somehow processed information (which made it organic), and unaccountably presented itself in patterns (waves). In short, physicists found themselves dealing with Wu Li—patterns of organic energy.
fn1 “. . . the hypothesis of quanta has led to the idea that there are changes in Nature which do not occur continuously but in an explosive manner.”—Max Planck, “Neue Bahnen der physikalischen Erkenntnis”, 1913, trans., F. d’Albe, Phil. Mag. vol. 28, 1914.
fn2 h = 6.63 × 10-27 erg-see
fn3 Bohr speculated that electronic orbits are arranged by nature at unvarying specific distances from the nucleus of the atom and that, when they absorb energy, the electrons in the atom jump outward from the orbit closest to the nucleus (the “ground state” of the atom) and eventually return to the innermost orbit, in the process emitting energy packets equal to the energy packets that they absorbed in jumping outward. Bohr proposed that when only a little energy is available (low heat), only small energy packets are absorbed by the electrons, and they do not jump out very far. When they return to their lowest energy level, they emit small energy packets, like those of red light. When more energy is available (high heat), larger energy packets are available, the electrons make bigger jumps outward and, on returning, they emit larger energy packets, like those of blue and violet light. Therefore, over low heat, metal glows red, and over high heat, it glows blue-white.
fn4 Each of Einstein’s major 1905 papers dealt with a fundamental physical constant: h, Planck’s constant (the photon hypothesis); k, Boltzmann’s constant (the analysis of Brownian movement); and c, the velocity of light (the special theory of relativity).
fn5 If we assume a particle aspect in the double-slit experiment we will violate the uncertainty relation unless we also assume non-locality.
fn6 An explanation other than “knowing” might be synchronicity, Jung’s acausal connecting principle.