THE IMPORTANCE OF nonsense hardly can be overstated. The more clearly we experience something as “nonsense”, the more clearly we are experiencing the boundaries of our own self-imposed cognitive structures. “Nonsense” is that which does not fit into the prearranged patterns which we have superimposed on reality. There is no such thing as “nonsense” apart from a judgmental intellect which calls it that.
True artists and true physicists know that nonsense is only that which, viewed from our present point of view, is unintelligible. Nonsense is nonsense only when we have not yet found that point of view from which it makes sense.
In general, physicists do not deal in nonsense. Most of them spend their professional lives thinking along well-established lines of thought. Those scientists who establish the established lines of thought, however, are those who do not fear to venture boldly into nonsense, into that which any fool could have told them is clearly not so. This is the mark of the creative mind; in fact, this is the creative process. It is characterized by a steadfast confidence that there exists a point of view from which the “nonsense” is not nonsense at all—in fact, from which it is obvious.
In physics, as elsewhere, those who most have felt the exhilaration of the creative process are those who best have slipped the bonds of the known to venture far into the unexplored territory which lies beyond the barrier of the obvious. This type of person has two characteristics. The first is a childlike ability to see the world as it is, and not as it appears according to what we know about it. This is the moral of the (child’s?) tale, “The Emperor’s New Clothes”. When the emperor rode naked through the streets, only a child proclaimed him to be without clothes, while the rest of his subjects forced themselves to believe, because they had been told so, that he wore his finest new clothing.
The child in us is always naive, innocent in the simplistic sense. A Zen story tells of Nan-in, a Japanese master during the Meiji era who received a university professor. The professor came to inquire about Zen. Nan-in served tea. He poured his visitor’s cup full, and then kept on pouring. The professor watched the overflow until he no longer could restrain himself.
“It is overfull. No more will go in!”
“Like this cup,” Nan-in said, “you are full of your own opinions and speculations. How can I show you Zen unless you first empty your cup?”
Our cup usually is filled to the brim with “the obvious”, “common sense”, and “the self-evident”.
Suzuki Roshi, who established the first Zen center in the United States (without trying, of course, which is very Zen), told his students that it is not difficult to attain enlightenment, but it is difficult to keep a beginner’s mind. “In the beginner’s mind,” he told them, “there are many possibilities, but in the expert’s there are few.” When his students published Suzuki’s talks after his death, they called the book, appropriately, Zen Mind, Beginner’s Mind. In the introduction, Baker Roshi, the American Zen Master, wrote:
The mind of the beginner is empty, free of the habits of the expert, ready to accept, to doubt, and open to all the possibilities . . .1
The beginner’s mind in science is wonderfully illustrated by the story of Albert Einstein and his theory of relativity. That is the subject of this chapter.
The second characteristic of true artists and true scientists is the firm confidence which both of them have in themselves. This confidence is an expression of an inner strength which allows them to speak out, secure in the knowledge that, appearances to the contrary, it is the world that is confused and not they. The first man to see an illusion by which men have flourished for centuries surely stands in a lonely place. In that moment of insight he, and he alone, sees the obvious which to the uninitiated (the rest of the world) yet appears as nonsense or, worse, as madness or heresy. This confidence is not the obstinacy of the fool, but the surety of him who knows what he knows, and knows also that he can convey it to others in a meaningful way.
The writer, Henry Miller, wrote:
I obey only my own instincts and intuition. I know nothing in advance. Often I put down things which I do not understand myself, secure in the knowledge that later they will become clear and meaningful to me. I have faith in the man who is writing, who is myself, the writer.2
The song-writer, Bob Dylan, told a press conference:
I just write a song and I know it’s going to be all right. I don’t even know what it’s going to say.3
An example of this kind of faith in the realm of physics was the theory of light quanta. In 1905, the accepted and proven theory of light was that light was a wave phenomenon. In spite of this, Einstein published his famous paper proposing that light was a particle phenomenon (see here). Heisenberg described this fascinating situation this way:
[In 1905] light could either be interpreted as consisting of electromagnetic waves, according to Maxwell’s theory, or as consisting of light quanta, energy packets traveling through space with high velocity [according to Einstein]. But could it be both? Einstein knew, of course, that the well-known phenomena of diffraction and interference can be explained only on the basis of the wave picture. He was not able to dispute the complete contradiction between this wave picture and the idea of the light quanta; nor did he even attempt to remove the inconsistency of this interpretation. He simply took the contradiction as something which would probably be understood much later.4
That is exactly what happened. Einstein’s thesis led to the wave-particle duality from which quantum mechanics emerged, and with it, as we know, a way of looking at reality and ourselves that is vastly different from that to which we were accustomed. Although Einstein is known popularly for his theories of relativity, it was his paper on the quantum nature of light that won him the Nobel Prize. It is also a fine example of confidence in nonsense.
What is nonsense and what is not, then, may be merely a matter of perspective.
“Wait a minute,” interrupts Jim de Wit. “My uncle, Weird George, believes that he is a football. Of course, we know that this is nonsense, but Uncle George thinks that we are mad. He is quite certain that he is a football. He talks about it constantly. In other words, he has abundant confidence in his nonsense. Does this make him a great scientist?”
No. In fact, weird George has a problem. Not only is he the only person who has this particular perspective, but also this particular perspective is in no way relative to that of any other observer, which brings us to the heart of Einstein’s special theory of relativity. (Einstein created two theories of relativity. The first theory is called the special theory of relativity. The second theory, which came later and is more general, is called the general theory of relativity. This chapter and the next are about the first theory, the special theory of relativity).
The special theory of relativity is not so much about what is relative as about what is not. It describes in what way the relative aspects of physical reality appear to vary, depending upon the point of view of different observers (actually depending upon their state of motion relative to each other), but, in the process, it defines the non-changing, absolute aspect of physical reality as well.
The special theory of relativity is not a theory that everything is relative. It is a theory that appearances are relative. What may appear to us as a ruler (physicists say “rod”) one foot long, may appear to an observer traveling past us (very fast) as being only ten inches long. What may appear to us as one hour, may appear to an observer traveling past us (very fast) as two hours. However, the moving observer can use the special theory of relativity to determine how our ruler and our clock appear to us (if he knows his motion relative to us) and, likewise, we can use the special theory of relativity to determine how our stick and our clock appear to the moving observer (if we know our motion relative to him).
If we were to perform an experiment at the same moment that the moving observer came past us, both we and the moving observer would see the same experiment, but each of us would record different times and distances, we with our rod and clock and he with his rod and clock. Using the special theory of relativity, however, each of us could transpose our data to the other’s frame of reference. The final numbers would come out the same for both of us. In essence, the special theory of relativity is not about what is relative, it is about what is absolute.
However, the special theory of relativity does show that appearances are dependent upon the state of motion of the observers. For example, the special theory of relativity tells us that (1) a moving object measures shorter in its direction of motion as its velocity increases until, at the speed of light, it disappears; (2) the mass of a moving object measures more as its velocity increases until, at the speed of light, it becomes infinite; and (3) moving clocks run more slowly as their velocity increases until, at the speed of light, they stop running altogether.
All of this is from the point of view of an observer to whom the object is moving. To an observer traveling along with the moving object, the clock keeps perfect time; ticking off sixty seconds each minute, and nothing appears to get any shorter or more massive. The special theory of relativity also tells us that space and time are not two separate things, but that together they form space-time, and that energy and mass are actually different forms of the same thing, mass-energy.
“This is not possible!” we say. “It is nonsense to think that increasing the velocity of an object increases its mass, decreases its length, and slows its time.”
Our cup runneth over.
These phenomena are not observable in everyday life because the velocities required to make them noticeable are those approaching the speed of light (186,000 miles per second). At the slow speeds that we encounter in the macroscopic world, these effects are virtually undetectable. If they were, we would discover that a car traveling down the freeway is shorter than it is at rest, weighs more than it does at rest, and that its clock runs slower than it does at rest. In fact, we even would find that a hot iron weighs more than a cold one (because energy has mass and heat is energy).
How Einstein discovered all of this is another version of “The Emperor’s New Clothes”.
Only Albert Einstein looked at two of the major puzzles of his day and saw them with a beginner’s mind. The result was the special theory of relativity. The first puzzle of Einstein’s time was the constancy of the speed of light. The second puzzle of Einstein’s time was the uncertainty, both physical and philosophical, about what it means to be moving or not moving.fn1
“Wait a minute,” we say. “What is uncertain about that? If I am sitting in a chair and another person walks past me, then the person walking past me is in motion, and I, sitting in my chair, am not in motion.”
“Quite right,” says Jim de Wit, appearing on cue, “but still, it is not that simple. Suppose that the chair in which you are sitting is on an airplane and that the person walking past you is a stewardess. Suppose also that I am on the ground watching both of you go by. From your point of view, you are at rest and the stewardess is in motion, but from my point of view, I am at rest and both of you are in motion. It all depends upon your frame of reference. Your frame of reference is the airplane, but my frame of reference is the earth.”
De Wit, as usual, has discovered the problem exactly. Unfortunately, he has not solved it. The earth itself hardly is standing still. Not only is it spinning on its axis like a top, it and the moon are revolving around a common center of gravity while both of them circle the sun at eighteen miles per second.
“That’s not fair,” we say. “Of course, it is true, but the earth does not seem to be moving to us who live on it. It is only in motion if we change our frame of reference from it to the sun. If we start playing that game, it is impossible to find anything in the entire universe that is ‘standing still’. From the point of view of the galaxy, the sun is moving; from the point of view of another galaxy, our galaxy is moving; from the point of view of a third galaxy, the first two galaxies are moving. In fact, from the point of view of each of them, the others are moving.”
“Nicely said,” laughs Jim de Wit, “and that is exactly the point. There is no such thing as something being absolutely at rest, unequivocally not moving. Motion, and the lack of it, is always relative to something else. Whether we are moving or not depends upon what frame of reference we use.”
The discussion above is not the special theory of relativity. In fact, the discussion above is a part of the Galilean relativity principle which is over three hundred years old. Any physical theory is a theory of relativity if, like Jim de Wit, it acknowledges the difficulty of detecting absolute motion or absolute non-motion. A theory of relativity assumes that the only kind of motion that we ever can determine is motion, or lack of it, relative to something else. Galileo’s principle of relativity says, in addition, that the laws of mechanics are equally valid in all frames of reference (physicists say “co-ordinate systems”) that move uniformly in relation to each other.
The Galilean relativity principle assumes that somewhere in the universe there exists a frame of reference in which the laws of mechanics are completely valid—that is, a frame of reference in which experiment and theory agree perfectly. This frame of reference is called an “inertial” frame of reference. An inertial frame of reference simply means a frame of reference in which the laws of mechanics are completely valid. All other frames of reference moving uniformly, relative to an inertial frame of reference, are also inertial frames of reference. Since the laws of mechanics are equally valid in all inertial frames of reference, this means that there is no way that we can distinguish between one inertial frame of reference and another by performing mechanical experiments in them.
Frames of reference moving uniformly, relative to each other, are co-ordinate systems that move with a constant speed and direction. In other words, they are frames of reference that move with a constant velocity. For example, if, by accident, we drop a book while standing in line at the library, the book falls directly downward in accordance with Newton’s law of gravity, and strikes the ground directly beneath the place from which it was dropped. Our frame of reference is the earth. The earth is moving at a fantastic speed on its trip around the sun, but this speed is constant.fn2
If we drop the same book while we are traveling on an ideally smooth train which is moving at a constant speed, the same thing happens. The book falls directly downward in accordance with Newton’s laws of gravitation, and strikes the floor of the train directly beneath the place from which it was dropped. This time, our frame of reference is the train. Because the train is moving uniformly, with no increases or decreases of speed, in relation to the earth, and because the earth is moving in a similar manner in relation to the train, the two frames of reference are moving uniformly relative to each other, and the laws of mechanics are valid in both of them. It does not matter in the least which of the frames of reference is “moving”. A person in either frame of reference can consider himself moving and the other frame of reference at rest (the earth is at rest and the train is moving) or the other way round (the train is at rest and the earth is moving). From the point of view of physics, there is no difference.
What happens if the engineer suddenly accelerates while we are doing our experiment? Then, of course, everything is upset. The falling book still will strike the floor of the train, but at a spot farther back since the floor of the train has moved forward beneath the book while it was falling. In this case, the train is not moving uniformly in relation to the earth, and the Galilean relativity principle does not apply.
Provided that all of the motion involved is uniformly relative, we can translate motion as perceived in one frame of reference into another frame of reference. For example, suppose that we are standing on the shore watching a ship move past us at thirty miles per hour. The ship is a frame of reference moving uniformly relative to us. There is a passenger, a man, standing on the deck of the ship, leaning against the railing. Since he is standing still, his velocity is the same as that of the ship, thirty miles per hour. (From his point of view, we are moving past him at thirty miles per hour).
Suppose now that the man begins to walk toward the front of the ship at three miles per hour. His velocity now, relative to us, is thirty-three miles per hour. The ship carries him forward at thirty miles per hour, and his walking adds three miles per hour to that. (You get to the top of an escalator faster if you walk).
Suppose that the man turns around and walks back toward the rear of the ship. His velocity relative to the ship is, again, three miles per hour, but his velocity relative to the shore is now twenty-seven miles per hour.
In other words, to calculate how fast this passenger moves relative to us, we add his velocity to the velocity of his co-ordinate system (the ship) if he is walking in the same direction that it is moving, and we subtract his velocity from the velocity of his co-ordinate system if he is walking in the opposite direction. This calculation is called a classical (Galilean) transformation. Knowing the uniform relative motion of our two frames of reference, we can transform the passenger’s velocity in reference to his own co-ordinate system (three miles per hour) into his velocity in reference to our co-ordinate system (thirty-three miles per hour).
The freeway provides abundant examples of classical transformations from one frame of reference to another. Suppose that we are driving at 75 miles per hour. We see a truck coming toward us. Its speedometer also reads 75 miles per hour. Making a classical transformation, we can say that, relative to us, the truck is approaching at 150 miles per hour, which explains why head-on collisions so often are fatal.
Suppose now that a car going in the same direction that we are going passes us. His speedometer reads 110 miles per hour. Again. making a classical transformation, we can say that, relative to us, he is departing our location at 35 miles per hour.
The transformation laws of classical mechanics are common sense. They say that, even though we cannot determine whether a frame of reference is absolutely at rest or not, we can translate velocities (and positions) from one frame of reference into velocities (and positions) in other frames of reference, provided that the frames of reference are moving uniformly, relative to each other. Furthermore, the Galilean relativity principle, from which Galilean transformations come, says that if the laws of mechanics are valid in any one frame of reference, they also are valid in any other frame of reference moving uniformly relative to it.
Unfortunately, there is one catch in all this. No one yet has found a co-ordinate system in which the laws of mechanics are valid!fn3
“But that’s impossible. What about the earth?”
Well, it is true that Galileo, who first probed the laws of classical mechanics, used the earth as a frame of reference, although not consciously. (The idea of co-ordinate systems did not come along until Descartes). However, our present measuring devices are more accurate than Galileo’s who occasionally even used his pulse (which means that the more excited he got, the more inaccurate his measurements became!). Whenever we reconstruct Galileo’s falling body experiments, we always find discrepancies between the theoretical results that we should get and the experimental results that we actually do get. These discrepancies are due to the rotation of the earth. The bitter truth is that the laws of mechanics are not valid for a co-ordinate system rigidly attached to the earth. The earth is not an inertial frame of reference. Since their very inception, the poor laws of classical mechanics have been left, so to speak, without a home. No one has discovered a co-ordinate system in which they manifest themselves perfectly.
This leaves us, from a physicist’s point of view, in a pretty mess. On the one hand, we have the laws of classical mechanics, which are indispensable to physics, and, on the other hand, these same laws are predicated upon a co-ordinate system which may not even exist.
This problem is related to relativity, which is the problem of determining absolute non-motion, in an intimate way. If such a thing as absolute non-motion were detected, then a co-ordinate system attached to it would be the long-lost inertial frame of reference, the co-ordinate system in which the classical laws of mechanics are perfectly valid. Then everything would make sense again because, given a frame of reference in which the classical laws of mechanics are valid, any frame of reference, the classical laws of mechanics at last would have a permanent mailing address.
Physicists do not enjoy theories with loose ends. Before Einstein, the problem of detecting absolute motion (or absolute non-motion—if we find one, we find the other), and the problem of finding an inertial co-ordinate system were, to say the least, loose ends. The entire structure of classical mechanics was based on the fact that somewhere, somehow, there must be a frame of reference in which the laws of classical mechanics are valid. The inability of physicists to find it made classical mechanics appear exactly like a huge castle built on sand.
Although no one, including Einstein, discovered absolute non-motion, the inability to detect it was a major concern of Einstein’s day. The second major controversy of Einstein’s day (not counting Planck’s discovery of the quantum) was an incomprehensible, logic-defying characteristic of light.
In the course of their experiments with the speed of light, physicists discovered something very strange. The speed of light disregards the transformation laws of classical mechanics. Of course, that’s impossible, but nevertheless, experiment after experiment proved just the opposite. The speed of light just happens to be the most nonsensical thing ever discovered. That is because it never changes.
“So light always travels at the same speed,” we ask, “what’s so strange about that?”
A physicist from the 1880’s might say, “You simply don’t understand the problem. The problem is that no matter what the circumstances of the measurement, no matter what the motion of the observer, the speed of light always measures 186,000 miles per second.”fn4
“Is this bad?” we say, beginning to sense that something is strange here.
“Worse,” says the physicist. “It’s impossible. Look,” he tells us, trying to calm himself, “suppose that we are standing still and that somewhere in front of us is a light bulb that also is standing still. The light bulb flashes on and off and we measure the velocity of the light that comes from it. What do you suppose that velocity will be?”
“186,000 miles per second,” we answer, “the speed of light.”
“Correct!” says the physicist, with a knowing look that makes us uncomfortable. “Now, suppose the light bulb still is standing still, but we are moving toward it at 100,000 miles per second. Now what will we measure the speed of the light to be?”
“286,000 miles per second,” we answer, “the speed of light (186,000 miles per second) plus our speed (100,000 miles per second).” (This is a typical example of a classical transformation).
“Wrong!” shouts the physicist. “That’s just the point. The speed of the light is still 186,000 miles per second.”
“Wait a minute,” we say. “That can’t be. You say that if the light bulb is at rest and we are at rest, the speed of photons emitted from it will measure the same to us as the speed of photons emitted from it when we are rushing toward the light bulb? That doesn’t make sense. When the photons are emitted, they are traveling at 186,000 miles per second. If we also are moving, and moving toward them, their velocity should measure that much faster. In fact, they should appear to be traveling with the speed at which they were emitted plus our speed. Their velocity should measure 186,000 miles per second plus 100,000 miles per second.”
“True,” says our friend, “but it doesn’t. It measures 186,000 miles per second, just as if we still were standing still.”
Pausing for that to sink in, he continues, “Now consider the opposite situation. Suppose that the light bulb still is standing still, and this time we are moving away from it at 100,000 miles per second. What will the velocity of the photons measure now?”
“86,000 miles per second?” we say, hopefully, “the speed of light minus our speed as we move away from the approaching photons?”
“Wrong, again!” exclaims our friend again. “It should, but it doesn’t. The speed of the photons still measures 186,000 miles per second.”
“This is very hard to believe. Do you mean that if a light bulb is at rest and we measure the speed of the photons emitted from it while we also are at rest, and if we then measure the speed of the photons from it while we are moving toward it, and lastly, if we measure the speed of the photons emitted from it while we are moving away from it, we get the same result in all three cases?”
“Exactly!” says the physicist. “186,000 miles per second.”fn5
“Do you have any evidence?” we ask him.
“Unfortunately,” he says, “I do. Two American physicists, Albert Michelson and Edward Morley, have just completed an experiment which seems to show that the speed of light is constant, regardless of the state of motion of the observer.”
“This can’t happen,” he sighs, “but it is happening. It just doesn’t make sense.”
The problem of absolute non-motion and the problem of the constancy of the speed of light converged in the Michelson-Morley experiment. The Michelson-Morley experiment (1887) was a crucial experiment. A crucial experiment is an experiment which determines the life or death of a scientific theory. The theory that was tested by the Michelson-Morley experiment was the theory of the ether.
The theory of the ether was that the entire universe lies in and is permeated by an invisible, tasteless, odorless substance that has no properties at all, and exists simply because it has to exist so that light waves can have something to propagate in. For light to travel as waves, according to the theory, something has to be waving. That something was the ether. The theory of the ether was the last attempt to explain the universe by explaining something. Interpreting the universe in terms of things (like the Great Machine idea) was the distinguishing characteristic of the mechanical view, which means all of physics from Newton until the middle 1800’s.
The ether, according to the theory, is everywhere and in everything. We live and perform our experiments in a sea of ether. To the ether, the hardest substance is as porous as a sponge to water. There are no doors to the ether. Although we move in the ether sea, the ether sea does not move. It is absolutely, unequivocally not moving.
Therefore, although the primary reason for the existence of the ether was to give light something to propagate through, its existence also solved the old problem of locating the original inertial co-ordinate system, that frame of reference in which the laws of mechanics are completely valid. If the ether existed (and it had to exist), the co-ordinate system attached to it was the co-ordinate system against which all others could be compared to see if they were moving or not.
The findings of Michelson and Morley gave a verdict of death to the theory of the ether.fn6 Equally important, they led to the mathematical foundations of Einstein’s revolutionary new theory.
The idea of the Michelson-Morley experiment was to determine the motion of the earth through the ether sea. The problem was how to do this. Two ships at sea can determine their motion relative to one another, but if only one ship moves through a smooth sea, it has no reference point against which to measure its progress. In the old days, seamen would throw a log overboard, and measure their progress relative to it. Michelson and Morley did the same thing, except that the log that they threw overboard was a beam of light.
Their experiment was conceptually simple and ingenious. If the earth is moving, they reasoned, and the ether sea is at rest, then the movement of the earth through the ether sea must cause an ether breeze. Therefore, a beam of light traveling against the ether breeze should have a slower velocity than a beam of light sent across the ether breeze. This is the essence of the Michelson-Morley experiment.
Every pilot knows that it takes longer to fly a given distance if one leg of the trip is against a head wind (even though the return leg is with a tail wind) than it takes to fly the same distance across the same wind. Similarly, thought Michelson and Morley, if the theory of the ether sea is correct, a light beam sent upstream against the ether breeze and then downstream with it will take longer to return to its starting point than a light beam sent back and forth across the ether breeze.
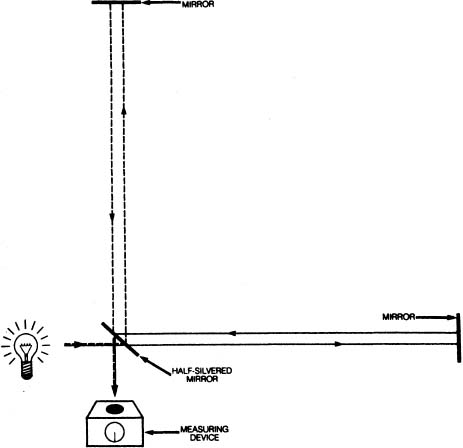
To establish and detect this difference in velocity, Michelson and Morley created a device called an interferometer (from the word, “interference”). It was designed to detect the interference pattern created by the two beams of light as they returned to a common point.

A light source emits a beam of light toward a half-silvered mirror (similar to the lenses in sunglasses that look like a mirror on one side, but are transparent from the other side). The original beam of light (![]() ) is split by the half-silvered mirror into two segments (
) is split by the half-silvered mirror into two segments (![]() ) (
) (![]() ), each of which travels an equal distance, but at right angles to each other, and back again. The two beams then reunite via the same half-silvered mirror and travel (
), each of which travels an equal distance, but at right angles to each other, and back again. The two beams then reunite via the same half-silvered mirror and travel (![]() ) into a measuring device. By observing the interference created by these converging beams in the measuring device, any difference in velocity between them can be determined accurately.
) into a measuring device. By observing the interference created by these converging beams in the measuring device, any difference in velocity between them can be determined accurately.
When the experiment was performed, not the slightest difference in velocity could be detected between the two beams of light. The interferometer was turned 90 degrees so that the beam going against the ether wind now was directed across it, and the beam going across the ether wind now was sent directly into it. Again not the slightest difference in velocity between the two beams could be detected.
In other words, the Michelson-Morley experiment had failed to prove the existence of the ether. Unless an explanation could be found, physicists would be faced with choosing between two unsettling alternatives: either (1) the earth is not moving (and Copernicus was wrong), or (2) the ether does not exist. Neither of these was very acceptable.
Michelson and Morley thought that perhaps the earth carried a layer of ether with it as it moved through the ether sea, just as it carries its atmosphere with it as it travels through space and, therefore, close to the surface of the earth, the ether breeze cannot be detected. No one had a better hypothesis until an Irishman named George Francis FitzGerald proposed (in 1892) an outrageous explanation.
FitzGerald reasoned that perhaps the pressure of the ether wind compresses matter just as an elastic object moving through water becomes shortened in the direction that it is traveling. If this were true, then the arm of the interferometer pointing into the ether wind would be somewhat shorter than the arm that is not pointing into it. Therefore, a reduction in the velocity of the light traveling into the ether wind and back might not be detected because the distance that the light travels also is reduced. In fact, if the amount by which the interferometer arm pointing into the ether wind is shortened just corresponds to the amount by which the velocity of the light traveling up that arm and back is reduced, then both beams of light in the experiment will reach the measuring device at exactly the same time (the beam with the higher velocity traversing a greater distance in the same time that the beam with the slower velocity traverses a lesser distance).
FitzGerald’s hypothesis had a major advantage over all the others. It was impossible to disprove. It said simply that there is a one-dimensional contraction (in the direction of motion) that increases as velocity increases. The catch is that everything contracts. If we want to measure the length of an object that is moving very fast compared to the speed of light, we have to catch up with it first, and when we do, according to the theory, the measuring stick that we are carrying with us also contracts. If the object measured seventeen inches at rest, it still would measure seventeen inches. Nor would anything look contracted because the lenses in our eyes also would contract, distorting them just enough to make everything look normal.
One year later a Dutch physicist, Hendrik Antoon Lorentz, while working on another problem, independently arrived at FitzGerald’s hypothesis. Lorentz, however, expressed his discovery in rigorous mathematical terms. This, of course, upgraded FitzGerald’s hypothesis to a position of respectability and it began to gain a surprising degree of acceptance, considering its fantasy-like quality. Lorentz’s mathematical formulations of the FitzGerald-Lorentz contraction became known as the Lorentz transformations.
The stage was now set. All of the scenery was in place. The failure to detect the ether. The Michelson-Morley experiment.fn7 The constancy of the speed of light. The FitzGerald-Lorentz contractions. The Lorentz transformations. These are the facts that continued to confuse physicists at the beginning of the century. All of them but Albert Einstein. When he looked at these pieces of scenery, what his beginner’s mind saw was the special theory of relativity.
fn1 Einstein’s point of departure for the special theory of relativity came from the conflict of classical relativity and Maxwell’s prediction of a light speed, “c”. An often-told story tells how Einstein tried to imagine what it would be like to travel as fast as a light wave. He saw, for example, that the hands on a clock would appear to stand still, since no other light waves from the clock would be able to catch up with him until he slowed down.
fn2 Although we do not experience it directly, the orbital motion of the earth is accelerating.
fn3 The fixed stars provide such a reference frame as far as defining non-rotation.
fn4 In a vacuum. The speed of light changes in matter depending upon the index of refraction of the matter: ![]()
fn5 The reverse situation (the source moves and the observer remains stationary) is explainable in terms of pre-relativistic physics. In fact, if light is assumed to be a wave phenomenon governed by a wave equation, it is expected that its measured velocity will be independent of the velocity of its source. The velocity of the sound waves reaching us from a jet plane, for example, does not depend upon the velocity of the aircraft. They propagate through a medium (the atmosphere) at a given velocity, from their point of origin, regardless of the motion of the plane (the frequency of the sound shifts as the source moves, e.g., the Doppler effect). Pre-relativity theory assumes a medium (like the atmosphere, for sound waves, or the ether, for light waves) through which the waves propagate. The paradox is that the measured velocity of light has been found (the Michelson-Morley experiment) to be independent of the motion of the observer. In other words, assuming a light wave propagating through a medium, how can we move through the same medium toward the approaching wave without increasing its measured velocity?
fn6 Quantum field theory resurrects a new kind of ether, e.g., particles are excited states of the featureless ground state of the field (the vacuum state). The vacuum state is so featureless and has such high symmetry that we cannot assign a velocity to it experimentally.
fn7 It is said that the reasoning process by which Einstein discpvered the special theory of relativity did not include the results of the Michelson-Morley experiment. However, the results of this well-publicized experiment were “in the air” for eighteen years prior to Einstein’s paper on special relativity (1905) and they led to the Lorentz transformations which became central to the mathematical formalism of special relativity.