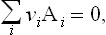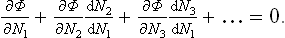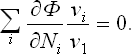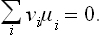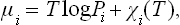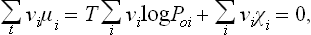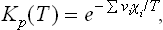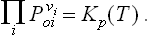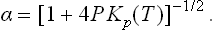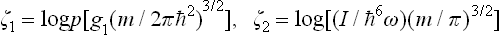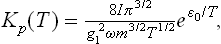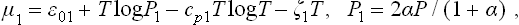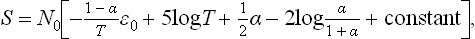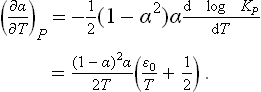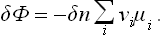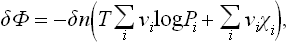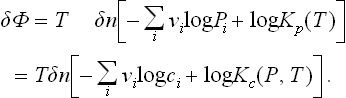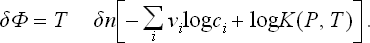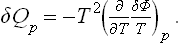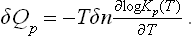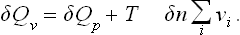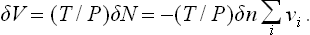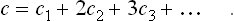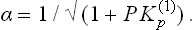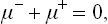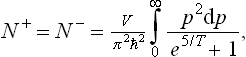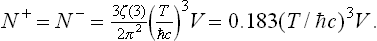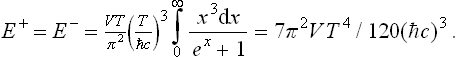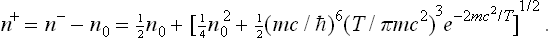CHEMICAL REACTIONS
Publisher Summary
A chemical reaction occurring in a mixture of reacting substances leads to the establishment of an equilibrium state in which the quantity of each of the substances that take part in the reaction no longer changes. This case of thermodynamic equilibrium is called chemical equilibrium. Any chemical reaction can take place in either direction; until equilibrium is reached, one direction predominates, but in equilibrium, the two opposite reactions occur at rates such that the total numbers of particles of each of the reacting substances remain constant. The object of thermodynamics as applied to chemical reactions is to study the chemical equilibrium and not the course of the reaction leading to that equilibrium. The state of chemical equilibrium is independent of how and under what conditions the reaction occurred; it depends on the conditions under which the mixture of reacting substances exists in equilibrium. In deriving the condition for chemical equilibrium, any desired assumptions concerning the course of the reaction can be made.
§ 101 The condition for chemical equilibrium
A CHEMICAL reaction occurring in a mixture of reacting substances ultimately leads to the establishment of an equilibrium state in which the quantity of each of the substances that take part in the reaction no longer changes. This case of thermodynamic equilibrium is called chemical equilibrium. Any chemical reaction can take place, in general, in either direction; until equilibrium is reached, one direction predominates, but in equilibrium the two opposite reactions occur at rates such that the total numbers of particles of each of the reacting substances remain constant. The object of thermodynamics as applied to chemical reactions is to study only the chemical equilibrium, not the course of the reaction leading to that equilibrium.
It is important to note that the state of chemical equilibrium is independent of how and under what conditions the reaction occurred;† it depends only on the conditions under which the mixture of reacting substances exists in equilibrium. In deriving the condition for chemical equilibrium, we can therefore make any desired assumptions concerning the course of the reaction.
First of all, we shall describe the method to be used for expressing the reaction. Chemical reactions are commonly written as symbolic equations, which, if all the terms are taken to one side, have the form
where the Al are the chemical symbols of the reacting substances, and the coefficients vi are positive or negative integers. For example, in the reaction 2H2+O2 = 2H2O or 2H2+O2-2H2O = 0 the coefficients are vHg = 2, vOg = 1, vHgO = −2.
Let us assume that the reaction occurs at constant temperature and pressure. In such processes the thermodynamic potential of the system tends to a minimum. In equilibrium, therefore, the potential Φ must have its least possible value (for given P and T). Let N1, N2, … be the numbers of particles of the various substances taking part in the reaction. Then the necessary condition for Φ to be a minimum can be written as the vanishing of the total derivative of Φ (for given P and T) with respect to one of the Ni, say N1:
The changes in the numbers Ni during the reaction are related by the reaction equation: it is clear that, if N1 changes by v1 each of the other Ni will change by vi, so that dNi = (vi/v1)dN1, dNi/dN1 = vi/v1. The foregoing equation may therefore be written
Finally, putting ∂Φ/∂N, = μi and multiplying by v1, we have
This is the required condition for chemical equilibrium. In order to obtain it, therefore, we must replace the symbols Ai by the corresponding chemical potentials μi in the equation of the chemical reaction. When several different reactions can occur in the mixture, the equilibrium condition will be a set of several equations such as (101.2), each obtained by the above method from the equation of the corresponding reaction.
It may be noted that the condition (101.2) retains its form even when the reacting substances are distributed in the form of solutes in two different phases in contact. This follows from the fact that in equilibrium the chemical potentials of each substance in either phase must be equal, in accordance with the conditions for phase equilibrium.
§ 102 The law of mass action
Let us apply the general condition for chemical equilibrium, derived in § 101, to reactions taking place in a gas mixture, assuming that the gas may be regarded as an ideal one.
The chemical potential of each gas in the mixture is (see § 93)
where Pi is the partial pressure of the ith gas in the mixture; Pi = ciP if P is the total pressure of the mixture and ci = Ni/N is the concentration of the gas in question, defined as the ratio of the number Ni of molecules of that gas to the total number N = ΣNi of molecules in the mixture.
It is now easy to write down the condition of chemical equilibrium for reactions in a mixture of gases. Substitution of (102.1) in (101.2) gives
where the P0i are the partial pressures of the gases in a state of chemical equilibrium.
we thus have
Instead of P0i we can substitute Pc0i, where the c0i are the concentrations of the gases in chemical equilibrium. Then
The quantity on the right of (102.3) or (102.4) is a function only of temperature and pressure, and does not depend on the initial amounts of the reacting gases: this quantity is called the chemical equilibrium constant, and the law expressed by formula (102.3) or (102.4) is called the law of mass action.
The dependence of the gas reaction equilibrium constant on the pressure is entirely determined by the factor P−Σvi on the right-hand side of equation 102.4; if the quantities of reacting substances are expressed in terms of their partial pressures, the equilibrium constant is independent of pressure. The determination of its dependence on temperature, however, requires further assumptions concerning the properties of the gases.
For example, if the gases have constant specific heats, a comparison of the expression (102.1) with formula (43.3) for the thermodynamic potential of such a gas shows that the functions χi(T) are of the form
where cpi is the specific heat and ζi the chemical constant of the gas. Substituting this expression in (102.2), we obtain for the equilibrium constant the formula
which is essentially an exponential function of temperature.
The law of mass action is valid also for reactions between solutes, provided that the solution may be regarded as weak. For the chemical potential of each solute has the form
The concentration ci is here defined as the ratio of the number of particles of the solute in question to the number of solvent particles (ci = ni/N). Substituting (102.7) in the equilibrium condition (101.2), we find in the same way
with the equilibrium constant
Unlike the case of gas reactions, the dependence of the equilibrium constant on the pressure here remains indeterminate.
If the reaction involves, as well as gases or solutes, substances in a pure condensed phase (i.e. not mixed with other substances), e.g. pure solids, then the equilibrium condition again leads to the law of mass action. Here, however, since the chemical potential of the pure phases depends only on the pressure and temperature, the left-hand side of the equation for the law of mass action will not involve the quantities of the pure phases, i.e. the product of the concentrations of the gases (or solutes) must be written as if the solids were absent. The latter affect only the dependence of the equilibrium constant on pressure and temperature.
If only gases and solids take part in the reaction, then, since the pressure of the gases is comparatively small, the chemical potential of the solids may be regarded as independent of the pressure, and the dependence of the equilibrium constant on the pressure remains the same as in (102.4). The sum Σvi in the exponent must of course denote only the sum of the coefficients of the gaseous substances in the reaction equation.
Finally, the law of mass action is valid also for reactions in weak solutions where the solvent as well as the solutes takes part in the reactions. For, when its chemical potential is substituted in the condition for chemical equilibrium, the small terms which contain the concentration may be omitted, and the potential then reduces to a quantity which depends only on temperature and pressure. Thus we again obtain the equation of the law of mass action, and its left-hand side again involves only the concentrations of the reacting solutes, not that of the solvent.
PROBLEMS
PROBLEM 1.
Find the degree of dissociation of a diatomic gas at high temperatures, if the gas molecule consists of identical atoms and has no spin or orbital angular momentum in the ground state.
SOLUTION.
The reaction has the form A2 = 2A. In these Problems, we shall use the suffixes 1 and 2 to denote quantities relating respectively to the atomic (A) and molecular (A2) components of the mixture. The degree of dissociation is defined as the ratio α = N1/2N0 of the number 
of dissociated molecules to the total number of molecules (that would exist in a non-dissociating gas) 
. In accordance with the law of mass action (102.3), we have
whence
The equilibrium constant KP is found by substituting in (102.6) the specific heats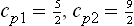 
the chemical constants
(see (45.4), (46.4), (49.8)), where m is the mass of the atom A, and g1 the statistical weight of the ground state of the atom A; at sufficiently high temperatures g1 = (2S+1) (2L+1), where S and L are the spin and orbital angular momentum of the atom.†
where 
=201−02 is the dissociation energy of the molecule.
SOLUTION.
The entropy of the gas may be calculated as the sum
the entropy of each component is expressed in terms of its chemical potential according to (43.6) and (43.3), and the equilibrium equation μ2 = 2μ1 is used. Expressing N1 and N2 in terms of N0 and α, writing the chemical potential as
and substituting the values of cp1 and cp2, we obtain
where the dissociation energy 0 is again used, and the constant represents the temperature-independent terms, which do not influence the required specific heat Cp = T(∂S/∂T)p. From (1) we calculate the derivative
with KP from (2). Now differentiating the entropy (3), we have finally
PROBLEM 3.
Determine the dependence of the concentration of hydrogen dissolved as H atoms in a metal on the pressure of H2 gas over the metal.
SOLUTION.
Regarding the process as a chemical reaction H2 = 2H, we can write the equilibrium condition as μH2=2μH; μH2 is written as the chemical potential of an ideal gas, μH2 = T log P + χ(T), and μH as that of the solute in a solution, μH = T log c + ψ. Since ψ depends only slightly on the pressure (cf. § 90), we find c = constant × √ P.
§ 103 Heat of reaction
A chemical reaction is accompanied by the absorption or evolution of heat. In the former case the reaction is said to be endothermic, and in the latter case exothermic. It is evident that, if any particular reaction is exothermic, the reverse reaction will be endothermic, and vice versa.
The amount of heat involved in a reaction depends on the conditions under which the reaction occurs. Hence, for instance, we must distinguish the heats of reaction at constant volume and at constant pressure (although the difference is usually quite small).
As in calculating the heat of solution (§ 91), we first find the maximum work which can be obtained by means of the chemical reaction. We call a reaction between one group of molecules as shown by the reaction equation an “elementary reaction”, and calculate the change in the thermodynamic potential of a mixture of reacting substances when a small number δn of elementary reactions take place, assuming that the reaction occurs at constant temperature and pressure. We have
The change in the number of molecules of the ith substance after δn elementary reactions is clearly δNi = − vi δn. Thus
In equilibrium δΦ/δn is zero, as we should expect.
Formula (103.1) is the general expression for the minimum work which must be done in order to bring about δn elementary reactions. It is also the maximum work which can be obtained from that number of reactions occurring in the reverse direction.
Let us first suppose that the reaction is between gases. Using the expression (102.1) for μi, we find
or, in terms of the equilibrium constant,
For reactions in solution we similarly find, using the expressions (102.7) and (102.9),
The sign of δΦ determines the direction in which the reaction takes place: since Φ tends to a minimum, for δΦ < 0 the reaction occurs in the forward direction (i.e. “from left to right” in the equation of the chemical reaction), while if δΦ > 0 the reaction will actually go in the opposite direction in the mixture concerned. It may be noted, however, that the direction of the reaction is also evident directly from the law of mass action: we form the product 
for the mixture in question and compare it with the value of the equilibrium constant for the reaction. If, for instance, we find that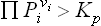 
, this means that the reaction will occur in the forward direction, so as to reduce the partial pressures of the original substances (which have positive vi in the reaction equation), and increase those of the reaction products (for which vi < 0).
We can now determine also the heat absorbed (or evolved, according to sign), again for δn elementary reactions. Formula (91.4) shows that this heat δQp is, for a reaction at constant temperature and pressure,
For reactions between gases we have, substituting (103.2),
We may note that δQp is simply proportional to δn and does not depend on the values of the concentrations at any instant. These formulae are therefore valid for any δn, whether small or not.
If Qp > 0, i.e. the reaction is endothermic, ∂ log K/∂T < 0, and the equilibrium constant decreases with increasing temperature. On the other hand, for an exothermic reaction (Qp < 0) the equilibrium constant increases with temperature. An increase in the equilibrium constant signifies that the chemical equilibrium is shifted back towards the re-formation of the initial substances— the reaction goes “from right to left”, so as to increase the product 
. Conversely, a decrease in the equilibrium constant signifies a shift of the equilibrium towards formation of the reaction products. In other words, we can formulate the following rule: heating shifts the equilibrium in the direction of the endothermic process, and cooling in the direction of the exothermic process. This rule is entirely in agreement with Le Chatelier’s principle.
For reactions between gases the heat of reaction at constant volume (and temperature) is also of interest. This quantity δQv is related in a simple manner to δQp. The quantity of heat absorbed in a process at constant volume is equal to the change in the energy of the system, whereas δQp is equal to the change in the heat function. Since E = W — PV, it is clear that δQv = = δQp - δ(PV) or, substituting PV = TΣNi and δNi = - vi δn,
Finally, let us determine the change in volume of a mixture of reacting substances as a result of a reaction occurring at constant pressure (and temperature). For gases, the problem is trivial:
In particular, reactions in which the total number of particles is unchanged (Σvi = 0) occur without change of volume.
For reactions in weak solutions we use the formula δV —∂δΦ/∂P and, substituting (103.3), we obtain
Thus a change in volume in the reaction is due to a pressure dependence of the equilibrium constant. In a similar way to the previous discussion of the temperature dependence, we easily deduce that an increase in pressure favours reactions in which the volume decreases (i.e. shifts the equilibrium in the direction of such reactions), and a decrease in pressure favours reactions which lead to an increase in volume, again in complete agreement with Le Chatelier’s principle.
§ 104 Ionisation equilibrium
At sufficiently high temperatures, collisions betwen gas particles may cause their ionisation. The existence of such thermal ionisation leads to the establishment of an equilibrium in which certain fractions of the total number of gas particles are in various stages of ionisation. Let us consider thermal ionisation of a monatomic gas; this is the most interesting case, since chemical compounds are usually completely dissociated before the onset of thermal ionisation.
Thermodynamically, ionisation equilibrium is a particular case of chemical equilibrium corresponding to a series of simultaneously occurring “ionisation reactions”, which may be written
where the symbol A0 denotes the neutral atom, A1, A2, … the singly, doubly, etc., ionised atoms and e− the electron. For these reactions the application of the law of mass action gives the set of equations
where c0 is the concentration of neutral atoms, c1, c2, … the concentrations of the various ions, and c the concentration of electrons (each defined as the ratio of the number of particles of the kind in question to the total number of particles, including electrons). To these equations we must add one which expresses the electrical neutrality of the gas as a whole:
Equation (104.2) and Equation (104.2) determine the concentrations of the various ions in ionisation equilibrium.
The equilibrium constants 
can be calculated without difficulty. All gases which take part in “reactions” (gases of neutral atoms, ions, or electrons) are monatomic and have constant specific heat 
, and their chemical constants are ζ = log [g(m/2πħ2)3/2], where m is the mass of a particle of the gas considered, and g the statistical weight of its ground state; for electrons, g = 2, while for atoms and ions g = (2L + 1)(2S + 1), where L and S are the orbital angular momentum and spin of the atom or ion.† Substituting these values in formula (102.6), we obtain the following expression for the required equilibrium constants:
(M. N. Saha, 1921) where m is the electron mass and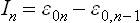 
the energy of the nth ionisation (nth ionisation potential) of the atom.
The degree of n-fold ionisation of the gas becomes of the order of unity as the temperature increases and the equilibrium constant 
decreases to a value of the order of unity. It is very important to note that, despite the exponential dependence of the equilibrium constant on temperature, this stage is reached not when T ˜ In but at considerably lower temperatures. The reason is that the coefficient of the exponential eIn/T is small: the quantity (P/T)(ħ2/mT)3/2 = (N/V) (ħ2/mT)3/2 is in general very small, being for T ˜ I of the order of the ratio of the atomic volume to the volume V/N per atom in the gas.
Thus the gas will be considerably ionised even at temperatures which are small compared with the ionisation energy, but the number of excited atoms in the gas will still be small, since the excitation energy of the atom is in general of the same order as the ionisation energy.
When T becomes comparable with the ionisation energy, the gas is almost completely ionised. At temperatures of the order of the binding energy of the last electron in the atom, the gas may be regarded as consisting of electrons and bare nuclei only.
The binding energy I1 of the first electron is usually much less than the subsequent ones In; there is therefore a range of temperatures in which the gas may be supposed to include only neutral atoms and singly charged ions. Defining the degree of ionisation α of the gas as the ratio of the number of ionised atoms to the total number of atoms, we have
and equation 104.2 gives 
, whence
This entirely determines the degree of ionisation as a function of pressure and temperature (in the temperature range considered).
§ 105 Equilibrium with respect to pair production
At extremely high temperatures, comparable with the rest energy† mc2 of the electron, collisions of particles in matter may be accompanied by the formation of electron-positron pairs. The number of particles itself then ceases to be a given quantity, and depends on the conditions of thermal equilibrium.
Pair production (and the reverse process, annihilation) can be regarded thermodynamically as a “chemical reaction” e+ + e− = γ, where the symbols e+ and e− denote a positron and an electron, and γ denotes one or more photons. The chemical potential of the photon gas is zero (§ 63). The condition of equilibrium for pair production is therefore
where μ− and μ+ are the chemical potentials of the electron and positron gases. It should be emphasised that μ here denotes the relativistic expression for the chemical potential, including the rest energy of the particles (cf. § 27), which plays an important part in pair production.
Even at temperatures T ˜ mc2, the number of pairs formed per unit volume is very large in comparison with the atomic electron density (see the next footnote). We can therefore suppose with sufficient accuracy that the number of electrons is equal to the number of positrons. Then μ− = μ+, and the condition (105.1) gives μ− = μ+ = 0, i.e. in equilibrium the chemical potentials of the electrons and positrons must be zero.
Electrons and positrons obey Fermi statistics; their number is therefore obtained by integrating the distribution (56.3) with μ = 0:
where is determined from the relativistic expression =c √(p2+m2c2).
For T « mc2, this number is exponentially small (∝ e− mc2/T). In the opposite case (T » mc2) we can put = cp, and formula (105.2) gives
The integral in this formula can be expressed in terms of the ζ function (see the second footnote to § 58), giving†
The energy of the positron and electron gases is similarly
This quantity is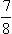 
of the energy of black-body radiation in the same volume.
PROBLEM
Determine the equilibrium density of electrons and positrons for T « mc2.
SOLUTION.
Using the expression (46.1a) for the chemical potential (to which mc2 must be added), we obtain
where n− = N−/V and n+ = N+/V are the electron and positron densities. If n0 is the initial electron density (in the absence of pair production), then n− = n+ + n0, and we find
†In particular, it is independent of whether a catalyst took part in the reaction.
†For reasons given below we may assume that all atoms and ions are in the ground state, even in a considerably ionised gas. If the atom (or ion) ground state has a fine structure, we assume that T is large compared with the intervals in this structure.
†The energy mc2 = 0.51×106 eV, so that the temperature mc2/k = 6×109 degrees.
†For T ˜ mc2 the volume per pair formed is ˜ (ħ/mc)3. This volume is very small in comparison with the atomic volume (the cube of the Bohr radius, (ħ2/me2)3).