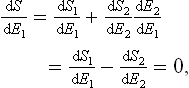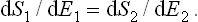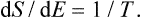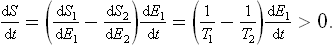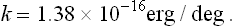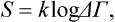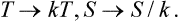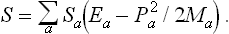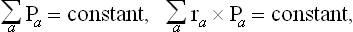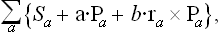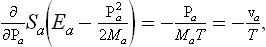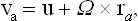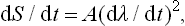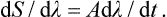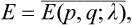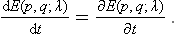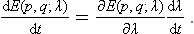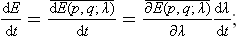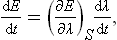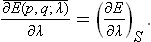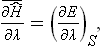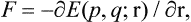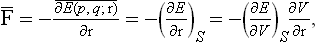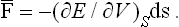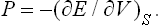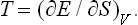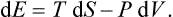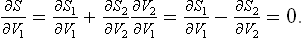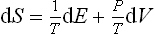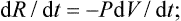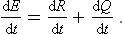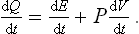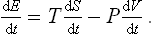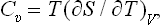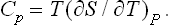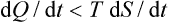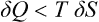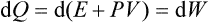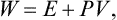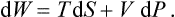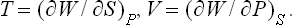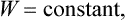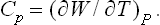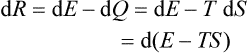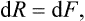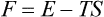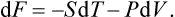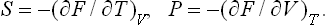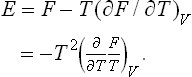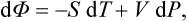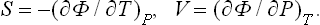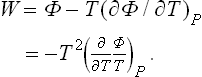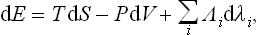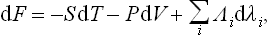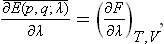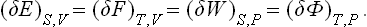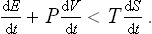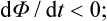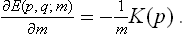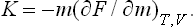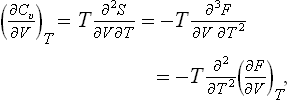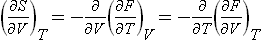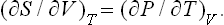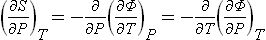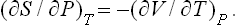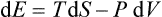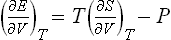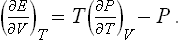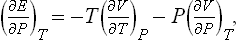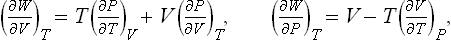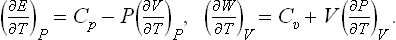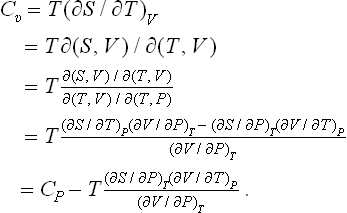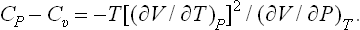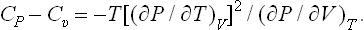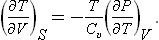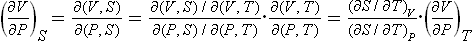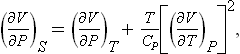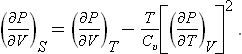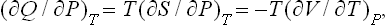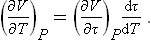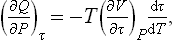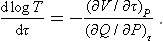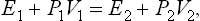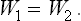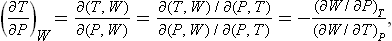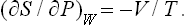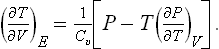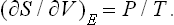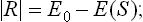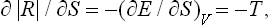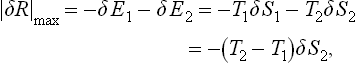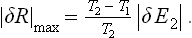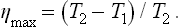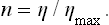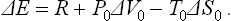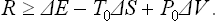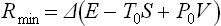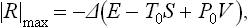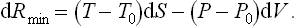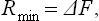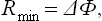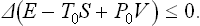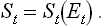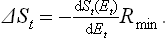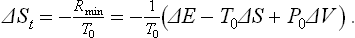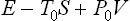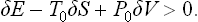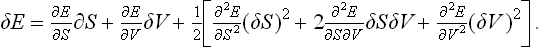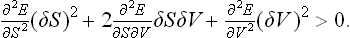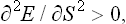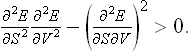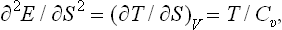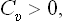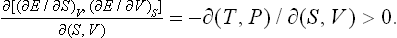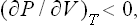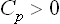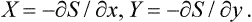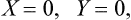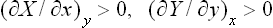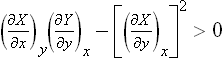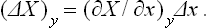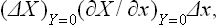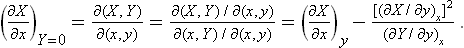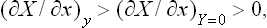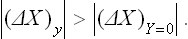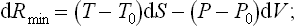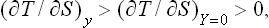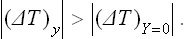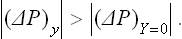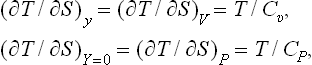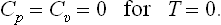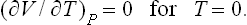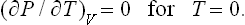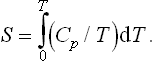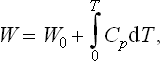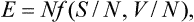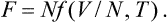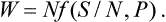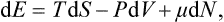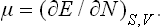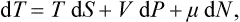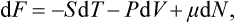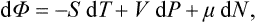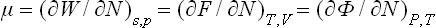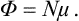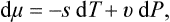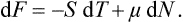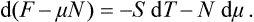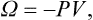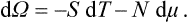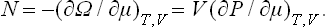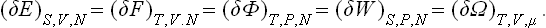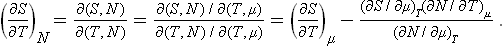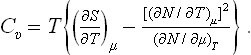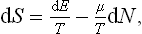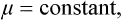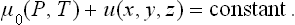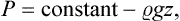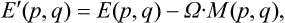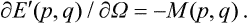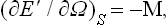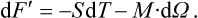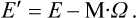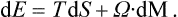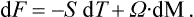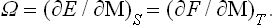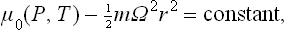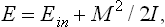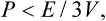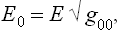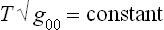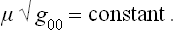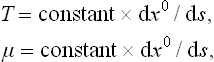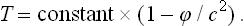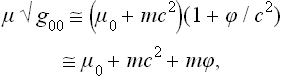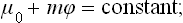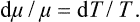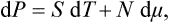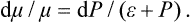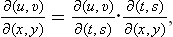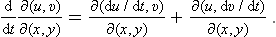THERMODYNAMIC QUANTITIES
Publisher Summary
Thermodynamic physical quantities describe macroscopic states of bodies. They include some which have a thermodynamic and a mechanical significance, such as energy and volume. This chapter discusses the thermodynamic relations. If a system is in a state of thermodynamic equilibrium, the derivative of the entropy with respect to the energy is the same for every part of it. The entropy is a dimensionless quantity. The temperature has the dimensions of energy and can be measured in energy units. Among the various kinds of external interactions to which a body is subject, those consisting in a change in the external conditions form a special group. In practice, the external conditions are determined by the fact that the body must have a prescribed volume. The chapter also describes the Joule-Thomson process and Nernst’s theorem.
§ 9 Temperature
Thermodynamic physical quantities are those which describe macroscopic states of bodies. They include some which have both a thermodynamic and a purely mechanical significance, such as energy and volume. There are also, however, quantities of another kind, which appear as a result of purely statistical laws and have no meaning when applied to non-macroscopic systems, for example entropy.
In what follows we shall define a number of relations between thermodynamic quantities which hold good whatever the particular bodies to which these quantities relate. These are called thermodynamic relations.
When thermodynamic quantities are discussed, the negligible fluctuations to which they are subject are usually of no interest. Accordingly, we shall entirely ignore such fluctuations, and regard the thermodynamic quantities as varying only with the macroscopic state of the body.†
Let us consider two bodies in thermal equilibrium with each other, forming a closed system. Then the entropy S of this system has its maximum value (for a given energy E of the system). The energy E is the sum of the energies E1 and E2 of the two bodies: E = E1+E2. The same applies to the entropy S of the system, and the entropy of each body is a function of its energy: S = S1(E1) + S2(E2). Since E2 = E—E1, E being a constant, S is really a function of one independent variable, and the necessary condition for a maximum may be written
whence
This conclusion can easily be generalised to any number of bodies in equilibrium with one another.
Thus, if a system is in a state of thermodynamic equilibrium, the derivative of the entropy with respect to the energy is the same for every part of it, i.e. is constant throughout the system. A quantity which is the reciprocal of the derivative of the entropy S of a body with respect to its energy E is called the absolute temperature T (or simply the temperature) of the body:
The temperatures of bodies in equilibrium with one another are therefore equal: T1 = T2.
Like the entropy, the temperature is seen to be a purely statistical quantity, which has meaning only for macroscopic bodies.
Let us next consider two bodies forming a closed system but not in equilibrium with each other. Their temperatures T1 and T2 are then different, in the course of time, equilibrium will be established between the bodies, and their temperatures will gradually become equal. During this process, their total entropy S = S1 + S2 must increase, i.e. its time derivative is positive:
Since the total energy is conserved, dE1/dt+dE2/dt = 0, and so
Let the temperature of the second body be greater than that of the first (T2 > T1). Then dE1/dt > 0, and dE2/dt < 0. In other words, the energy of the second body decreases and that of the first increases. This property of the temperature may be formulated as follows: energy passes from bodies at higher temperature to bodies at lower temperature.
The entropy S is a dimensionless quantity. The definition (9.1) therefore shows that the temperature has the dimensions of energy, and so can be measured in energy units, for example ergs. In ordinary circumstances, however, the erg is too large a quantity, and in practice the temperature is customarily measured in its own units, called degrees Kelvin or simply degrees. The conversion factor between ergs and degrees, i. e. the number of ergs per degree, is called Boltzmann’s constant and is usually denoted by k; its value is†
In all subsequent formulae the temperature will be assumed measured in energy units. To convert to the temperature measured in degrees, in numerical calculations, we need only replace T by kT. The continual use of the factor k, whose only purpose is to indicate the conventional units of temperature measurement, would merely complicate the formulae.
If the temperature is in degrees, the factor k is usually included in the definition of entropy:
instead of (7.7), in order to avoid the appearance of k in the general relations of thermodynamics. Then formula (9.1) defining the temperature, and therefore all the general thermodynamic relations derived subsequently in this chapter, are unaffected by the change to degrees.
Thus the rule for conversion to degrees is to substitute in all formulae
§ 10 Macroscopic motion
As distinct from the microscopic motion of molecules, the macroscopic motion is that in which the various macroscopic parts of a body participate as a whole. Let us consider the possibility of macroscopic motion in a state of thermodynamic equilibrium.
Let the body be divided into a large number of small (but macroscopic) parts, and let Ma, Ea and Pa denote the mass, energy and momentum of the ath part. The entropy Sa of each part is a function of its internal energy, i.e. the difference between its total energy Ea and the kinetic energy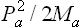 
of its macroscopic motion.‡ The total entropy of the body can therefore be written
We shall assume that the body is a closed system. Then its total momentum and angular momentum are conserved, as well as its energy:
where ra is the radius vector of the ath part. In a state of equilibrium, the total entropy S of the body as a function of the momenta Pa has a maximum subject to the conditions (10.2). Using the familiar Lagrange’s method of undetermined multipliers, we find the necessary conditions for a maximum by equating to zero the derivatives with respect to Pa of the sum
where a and b are constant vectors. Differentiation of Sa with respect to Pa gives,† by the definition of the temperature,
where va = Pa/Ma is the velocity of the ath part of the body. Differentiation of (10.3) therefore gives
or
where u = Ta and Ω = Tb are constant vectors.
This result has a simple physical significance. If the velocities of all the parts of a body are given by formula (10.4) with the same u and Ω, this means that we have a translational motion of the body as a whole with constant velocity u and a rotation of the body as a whole with constant angular velocity Ω. Thus we arrive at the important result that in thermodynamic equilibrium a closed system can execute only a uniform translational and rotational motion as a whole. No internal macroscopic motion is possible in a state of equilibrium.‡
In what follows we shall usually consider bodies at rest, and the energy E will accordingly be the internal energy of the body.
So far we have made use only of the necessary condition for a maximum of entropy as a function of the momenta, but not of the sufficient condition to be imposed on the second derivatives. It is easy to see that the latter condition leads to the very important result that the temperature must be positive: T > 0.† To deduce this, it is not in fact necessary to calculate the second derivatives; instead, we can argue as follows.
Let us consider a body forming a closed system, at rest as a whole. If the temperature were negative, the entropy would increase with decreasing argument. Since the entropy tends to increase, the body would spontaneously seek to break up into dispersing parts (with total momentum ΣPa = 0), so that the argument of each Sa in the sum (10.1) should take its least possible value. In other words, bodies in equilibrium could not exist with T < 0.
The following point should be noted, however. Although the temperature of a body or any part of it can never be negative, there may exist partial equilibria in which the temperature corresponding to a particular group of degrees of freedom of the body is negative. This is further discussed in § 73.
§ 11 Adiabatic processes
Among the various kinds of external interactions to which a body is subject, those which consist in a change in the external conditions form a special group. By “external conditions” we mean in a wide sense various external fields. In practice the external conditions are most often determined by the fact that the body must have a prescribed volume. In one sense this case may also be regarded as a particular type of external field, since the walls which limit the volume are equivalent in effect to a potential barrier which prevents the molecules in the body from escaping.
If the body is subject to no interactions other than changes in external conditions, it is said to be thermally isolated. It must be emphasised that, although a thermally isolated body does not interact directly with any other bodies, it is not in general a closed system, and its energy may vary with time.
In a purely mechanical way, a thermally isolated body differs from a closed system only in that its Hamiltonian (the energy) depends explicitly on the time: E = E(p, q, t), because of the variable external field. If the body also interacted directly with other bodies, it would have no Hamiltonian of its own, since the interaction would depend not only on the coordinates of the molecules of the body in question but also on those of the molecules in the other bodies.
This leads to the result that the law of increase of entropy is valid not only for closed systems but also for a thermally isolated body, since here we regard the external field as a completely specified function of coordinates and time, and in particular neglect the reaction of the body on the field. That is, the field is a purely mechanical and not a statistical object, whose entropy can in this sense be taken as zero. This proves the foregoing statement.
Let us suppose that a body is thermally isolated, and is subject to external conditions which vary sufficiently slowly. Such a process is said to be adiabatic. We shall show that, in an adiabatic process, the entropy of the body remains unchanged, i.e. the process is reversible.
We shall describe the external conditions by certain parameters which are given functions of time. For example, suppose that there is only one such parameter, which we denote by λ. The time derivative dS/dt of the entropy will depend in some manner on the rate of variation dλ/dt of the parameter λ. Since dλ/dt is small, we can expand dS/dt in powers of dλ/dt. The zero-order term in this expansion, which does not involve dλ/dt, is zero, since if dλ/dt = 0 then dS/dt = 0 also, because the entropy of a closed system in thermodynamic equilibrium must remain constant under constant external conditions. The first-order term, which is proportional to dλ/dt, must also be zero, since this term changes sign with dλ/dt, whereas dS/dt is always positive, according to the law of increase of entropy. Hence it follows that the expansion of dS/dt begins with the second-order term, i.e. for small dλ/dt we have
or
Thus, when dλ/dt tends to zero, so does dS/dλ, which proves that the adiabatic process is reversible.
It must be emphasised that, although an adiabatic process is reversible, not every reversible process is adiabatic. The condition for a process to be reversible requires only that the total entropy of the whole of a closed system be constant, while the entropies of its individual parts may either increase or decrease. In an adiabatic process, a stronger condition holds: the entropy of a body which is only a part of a closed system also remains constant.
We have defined an adiabatic process as one which is sufficiently slow. More precisely, we can say that the external conditions must change so slowly that at any instant the body may be regarded as being in a state of equilibrium corresponding to the prevailing external conditions. That is, the process must be slow in comparison with the processes leading to the establishment of equilibrium in the body concerned.†
We may derive a formula to calculate by a purely thermodynamic method various mean values. To do so, we assume that a body undergoes an adiabatic process, and determine the time derivative dE/dt of its energy. By definition, the thermodynamic energy is
where E(p, q; λ) is the Hamiltonian of the body, depending on λ as a parameter. We know from mechanics that the total time derivative of the Hamiltonian is equal to its partial time derivative (see Mechanics, § 40):
In the present case E(p, q; λ) depends explicitly on the time through λ(t), and we can therefore write
Since the operations of averaging over the statistical distribution and differentiating with respect to time can clearly be interchanged, we have
the derivative dλ/dt is a given function of time, and can be taken outside the averaging.
It is very important that, since the process is adiabatic, the mean value of the derivative ∂E(p, q; λ)/∂λ in (11.1) can be taken as the mean value over the statistical distribution corresponding to equilibrium for a given value of the parameter λ, i.e. for the external conditions prevailing at a given instant.
The derivative dE/dt can also be written in another form by regarding the thermodynamic quantity E as a function of the entropy S of the body and the external parameters λ. Since, in an adiabatic process, the entropy S remains constant, we have
where the subscript to the parenthesis indicates that the derivative is taken for constant S.
Comparison of (11.1) and (11.2) shows that
This is the required formula. It enables us to calculate thermodynamically the mean values (over the equilibrium statistical distribution) of quantities of the form ∂E(p, q; λ)/∂λ. Such quantities are continually encountered when studying the properties of macroscopic bodies, and in consequence formula (11.3) is of great importance in statistical physics. It appears in the calculation of various forces acting on a body (the parameters λ being the coordinates of a particular part of the body; see § 12), the calculation of the magnetic or electric moment of bodies (the parameters λ being the magnetic or electric field strengths), and so on.
The arguments given here for classical mechanics are entirely applicable to the quantum theory, except that the energy E(p, q; λ) must be everywhere replaced by the Hamiltonian operator Ĥ. Then formula (11.3) becomes
the bar denoting complete statistical averaging (which automatically includes the quantum averaging).
§ 12 Pressure
The energy E of a body, as a thermodynamic quantity, has the property of being additive: the energy of the body is equal to the sum of the energies of its individual (macroscopic) parts.† Another fundamental thermodynamic quantity, the entropy, also has this property.
The additivity of the energy and the entropy leads to the following important result. If a body is in thermal equilibrium, we can say that, for a given energy, the entropy depends only on the volume of the body, and not on its shape; the same is true of the energy for a given entropy.† For a change in the shape of the body can be regarded as a rearrangement of its individual parts, and so the entropy and energy, being additive, will remain unchanged. Here, of course, it is assumed that the body is not in an external field of force, so that the motion of the parts of the body in space does not involve a change in their energy.
Thus the macroscopic state of a body at rest in equilibrium is entirely determined by only two quantities, for example the volume and the energy. All other thermodynamic quantities can be expressed as functions of these two. Of course, because of this mutual dependence of the various thermodynamic quantities, any other pair could be regarded as the independent variables.
Let us now calculate the force exerted by a body on the surface bounding its volume. According to the formulae of mechanics, the force acting on a surface element ds is
where E(p, q; r) is the energy of the body as a function of the coordinates and momenta of its particles and of the radius vector of the surface element considered, which here acts as an external parameter. Averaging this equation and using formula (11.3), we obtain
where V is the volume. Since the change in volume is ds·dr, we have ∂V/∂r = ds, the surface element, and so
Hence we see that the mean force on a surface element is normal to the element and proportional to its area (Pascal’s law). The magnitude of the force per unit area is
This quantity is called the pressure.
In defining the temperature by formula (9.1) we were essentially considering a body which is not in direct contact with any other bodies, and in particular is not surrounded by any external medium. Under these conditions it was possible to speak of the change in energy and entropy of the body without making more specific the nature of the process. In the general case of a body in an external medium, or surrounded by the walls of a vessel, formula (9.1) must be made more precise. For if during the process the volume of the body changes, this will necessarily affect the state of the bodies in contact with it, and in order to define the temperature we should have to take into consideration at the same time all the bodies in contact (for example, both the body in question and the vessel containing it). If it is desired to define the temperature in terms of thermodynamic quantities for the given body only, its volume must be regarded as constant. In other words, the temperature is defined as the derivative of the energy of the body with respect to its entropy, taken at constant volume:
The equations (12.1), Equation (12.2) can also be written together as a relation between differentials:
This is one of the most important relations in thermodynamics.
The pressures of bodies in equilibrium with one another are equal. This follows immediately from the fact that thermal equilibrium necessarily presupposes mechanical equilibrium; in other words, the forces exerted on each other by any two of these bodies at their surface of contact must be equal in magnitude and opposite in direction, and thus balance.
The equality of pressures in equilibrium can also be derived from the condition of maximum entropy, in the same way as the equality of temperatures was shown in § 9. To do this, we consider two parts, in contact, of a closed system in equilibrium. One necessary condition for the entropy to be a maximum is that it should be a maximum with respect to a change in the volumes V1 and V2 of these two parts when the states of the other parts undergo no change (this means, in particular, that V1 + V2 remains constant). If the entropies of the two parts are S1 and S2, we have
From the relation (12.3) in the form
it is seen that ∂S/∂V = P/T, and so P1/T1 = P2/T2. Since the temperatures T1 and T2 are the same in equilibrium, we therefore find that the pressures are equal, P1 = P2.
It must be remembered that, when thermal equilibrium is established, the equality of pressures (i.e. mechanical equilibrium) is reached much more rapidly than that of temperatures, and so cases are often met with in which the pressure is constant throughout a body but the temperature is not. The reason is that the non-constancy of pressure is due to the presence of uncompensated forces; these bring about macroscopic motion so as to equalise the pressure much more rapidly than the equalisation of temperature, which does not involve macroscopic motion.
It is easy to see that the pressure must be positive in any equilibrium state: when P > 0 we have (∂S/∂V)E > 0, and the entropy could increase only by an expansion of the body, which is prevented by the surrounding bodies. If P < 0, however, then we should have (∂S/∂V)E < 0, and the body would spontaneously contract so as to increase its entropy.
There is, however, an important difference between the requirements of positive temperature and positive pressure. Bodies of negative temperature would be completely unstable and cannot exist in Nature. States (non-equilibrium) of negative pressure can exist in Nature with restricted stability. The reason is that the spontaneous contraction of the body involves “detaching” it from the walls of the vessel or the formation of cavities within it, that is, the formation of a new surface, and this leads to the possibility of the existence of negative pressures in what are called metastable states.†
§ 13 Work and quantity of heat
The external forces applied to a body can do work on it, which is determined, according to the general rules of mechanics, by the products of these forces and the displacements which they cause. This work may serve to bring the body into a state of macroscopic motion (or in general to change its kinetic energy), or to move the body in an external field (for instance, to raise it against gravity). We shall, however, be mainly interested in cases where the volume of a body is changed as a result of work done on it (i.e. the external forces compress the body but leave it at rest as a whole).
We shall everywhere regard as positive an amount of work R done on a given body by external forces. Negative work (R < 0) will correspondingly mean that the body itself does work (equal to | R |) on some external objects (for example, in expanding).
Bearing in mind that the force per unit area of the surface of the body is the pressure, and that the product of the area of a surface element and its displacement is the volume swept out by it, we find that the work done on the body per unit time when its volume changes is
in compression, dV/dt < 0, so that dR/dt > 0. This formula is applicable to both reversible and irreversible processes; only one condition need be satisfied, namely that throughout the process the body must be in a state of mechanical equilibrium, i.e. at each instant the pressure must be constant throughout the body.
If the body is thermally isolated, the whole of the change in its energy is due to the work done on it. In the general case of a body not thermally isolated, in addition to the work done, the body gains or loses energy by direct transfer from or to other bodies in contact with it. This part of the change in energy is called the quantity of heat Q gained or lost by the body. Thus the change in the energy of the body per unit time may be written
Like the work, the heat will be regarded as positive if gained by the body from external sources.
The energy E in (13.2) must, in general, be understood as the total energy of the body, including the kinetic energy of its macroscopic motion. We shall, however, usually consider the work corresponding to the change in volume of a body at rest, in which case the energy reduces to the internal energy of the body.
Under conditions where the work is defined by formula (13.1), we have for the quantity of heat
Let us assume that at every instant throughout the process the body may be regarded as being in a state of thermal equilibrium corresponding to its energy and volume at that instant; it must be emphasised that this does not mean that the process is necessarily reversible, since the body may not be in equilibrium with surrounding bodies. Then, from the relation (12.3), which gives the differential of the function E(S, V), the energy of the body in the equilibrium state, we can put
Comparison with (13.3) shows that
The work dR and the quantity of heat dQ gained by the body in an infinitesimal change of state are not the total differentials of any quantities.† Only the sum dQ + dR, i.e. the change in energy dE, is a total differential. We can therefore speak of the energy E in a given state, but not, for example, of the quantity of heat which a body possesses in a given state. In other words, the energy of the body cannot be divided into thermal and mechanical parts; this is possible only when considering the change in energy. The change in energy when a body goes from one state to another can be divided into the quantity of heat gained or lost by the body and the work done on it or by it. This division is not uniquely determined by the initial and final states of the body, but depends also on the nature of the process itself. That is, the work and the quantity of heat are functions of the process undergone by the body and not only of its initial and final states. This is seen particularly when the body undergoes a cyclic process, starting and finishing in the same state. The change in energy is then zero, but the body may gain or lose a quantity of heat or work. Mathematically this corresponds to the fact that the integral of the total differential dE around a closed circuit is zero, but the integral of dQ or dR, which are not total differentials, is not zero.
The quantity of heat which must be gained in order to raise the temperature of the body by one unit is called its specific heat. This clearly depends on the conditions under which the heating takes place. A distinction is usually made between the specific heat at constant volume Cυ and that at constant pressure Cp. Clearly
Let us consider cases where formula (13.4) for the quantity of heat is inapplicable, but at the same time it is possible to establish certain inequalities for this quantity. There exist processes in which the body is not in thermal equilibrium although the temperature (and pressure) are constant throughout the body; for example, chemical reactions in a homogeneous mixture of reactants. Owing to the irreversible process (the chemical reaction) occurring in the body, its entropy increases independently of the heat gained, and so we can say that the inequality
holds.
Another case where a similar inequality can be stated is an irreversible process in which the body goes from one equilibrium state to another neighbouring one but is not in equilibrium during the process.† Then the inequality
holds between the quantity of heat δQ gained by the body in this process and its entropy change δS.
§ 14 The heat function
If the volume of a body remains constant during a process, then dQ = dE, i.e. the quantity of heat gained by the body is equal to the change in its energy. If the process occurs at constant pressure, the quantity of heat can be written as the differential
of a quantity
called the heat function of the body.‡ The change in the heat function in processes occurring at constant pressure is therefore equal to the quantity of heat gained by the body.
It is easy to find an expression for the total differential of the heat function. Putting dE = T dS - P dV and d W = dE + P dV+ V dP, we have
From this it follows that
If the body is thermally isolated (which, it will be remembered, does not imply that it is a closed system), dQ = 0, and (14.1) shows that, in processes occurring at constant pressure and involving a thermally isolated body,
i.e. the heat function is conserved.
The specific heat Cυ can be written, using the relation dE = T dS – P dV, as
Similarly, we have for the specific heat Cp
We see that at constant pressure the heat function has properties similar to those of the energy at constant volume.
§ 15 The free energy and the thermodynamic potential
The work done on a body in an infinitesimal isothermal reversible change of state can be written as a differential:
or
where
is another function of the state of the body, called the free energy. Thus the work done on the body in a reversible isothermal process is equal to the change in its free energy.
Let us find the differential of the free energy. Substituting dE = T dS − P dV and dF = dE−TdS-S dT, we have
Hence it is evident that
Using the relation E = F + TS, we can express the energy in terms of the free energy as
Formulae (12.1), (12.2), (14.4) and (15.4) show that, if we know any of the quantities E, W and F as a function of the corresponding two variables and take its partial derivatives, we can determine all the remaining thermodynamic quantities. For this reason E, W and Fare called thermodynamic potentials (by analogy with the mechanical potential) or characteristic functions: the energy E with respect to the variables S, V; the heat function W with respect to S, P; the free energy F with respect to V, T.
We still lack a thermodynamic potential with respect to the variables P, T To derive this we substitute in (15.3) P dV = d(PV)–V dP, take d(PV) to the left-hand side of the equation, and obtain
with a new quantity
called the thermodynamic potential (in a restricted sense of the term).†
From (15.6) we clearly have
The heat function is expressed in terms of Φ in the same way as E in terms of F:
If there are other parameters λi besides the volume which define the state of the system, the expression for the differential of the energy must be augmented by terms proportional to the differentials dλi:
where the Λi are some functions of the state of the body. Since the transformation to other potentials does not affect the variables λi, it is clear that similar terms will be added to the differentials of F, Φ, W:
etc. Hence the quantities Λi can be obtained by differentiation with respect to λi, of any of these potentials (it must be remembered which other variables are treated as constant in the differentiation). Using also formula (11.3), we can write down the analogous relation
which expresses the mean value of the derivative of the Hamiltonian with respect to any parameter as the derivative of the free energy with respect to that parameter (and similar relations involving the derivatives of Φ and W).
The following point may be noted. If the values of the parameters λi, change slightly, the quantities E, F, W and Φ will also undergo small changes. It is evident that these changes will be equal if each is considered for the appropriate pair of constant quantities:
This statement, which we call the theorem of small increments, will be used several times below.
The free energy and the thermodynamic potential have an important property which determines the direction in which they change in various irreversible processes. From the inequality (13.7), substituting dQ/dt from (13.3), we obtain
Let us assume that the process is isothermal and occurs at constant volume (T = constant, V = constant). Then this inequality may be written
Thus irreversible processes occurring at constant temperature and constant volume are accompanied by a decrease in the free energy of the body.
Similarly, for P = constant and T = constant the inequality (15.13) becomes
that is, irreversible processes occurring at constant temperature and constant pressure are accompanied by a decrease in the thermodynamic potential.†
Correspondingly, in a state of thermal equilibrium the free energy and the thermodynamic potential have minimum values, the former with respect to all changes of state with T and V constant, and the latter with respect to changes of state with T and P constant.
PROBLEM
How can the mean kinetic energy of the particles in a body be calculated if the formula for its free energy is known?
SOLUTION.
The Hamiltonian function (or, in the quantum case, the Hamiltonian operator) may be written in the form E(p, q) = U(q)+K(p), where U(q) is the potential energy of interaction of the particles in the body, and K(p) their kinetic energy. The latter is a quadratic function of the momenta, inversely proportional to the particle mass m (for a body consisting of identical particles). Regarding m as a parameter, we can therefore write
Then, applying formula (15.11), we obtain the mean kinetic energy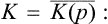 
§ 16 Relations between the derivatives of thermodynamic quantities
In practice the most convenient, and the most widely used, pairs of thermodynamic variables are T, V and T, P. It is therefore necessary to transform various derivatives of the thermodynamic quantities with respect to one another to different variables, both dependent and independent.
If V and T are used as independent variables, the results of the transformation can be conveniently expressed in terms of the pressure P and the specific heat Cυ (as functions of V and T). The equation which relates the pressure, volume and temperature is called the equation of state for a given body. Thus the purpose of the formulae in this case is to make it possible to calculate various derivatives of thermodynamic quantities from the equation of state and the specific heat Cυ.
Similarly, when P and T are taken as the basic variables the results of the transformation should be expressed in terms of V and Cp (as functions of P and T).
Here it must be remembered that the dependence of Cυ on V or of Cp on P (but not on the temperature) can itself be determined from the equation of state. It is easily seen that the derivative (∂Cυ/∂V)T can be transformed so that it is defined in terms of the function P(V, T). Using the fact that S = −(∂F/∂T)υ, we have
and since (∂F/∂V)T = −P, we have the required formula
formulae (15.8) being used in the calculation.
We shall show how some of the thermodynamic derivatives most often encountered may be transformed.
The derivatives of the entropy with respect to volume or pressure can be calculated from the equation of state by means of the following formulae, which are a direct consequence of the expressions for the differentials of the thermodynamic quantities. We have
or
Similarly
or
The derivative (∂E/∂V)T is calculated from the equation
as
or, substituting (16.3),
Similarly we can derive
Finally, we shall show how the specific heat Cυ may be calculated from the specific heat Cp and the equation of state, using T and P as the basic variables. Since Cυ = T(∂S/∂T)V, we have to transform the derivative (∂S/∂T)V to different independent variables. A transformation of this type is most simply effected by the use of Jacobians.† We write
Substituting (16.4), we obtain the required formula:
Similarly, transforming Cp = T(∂S/∂T)P to the variables T, V, we can derive the formula
The derivative (∂P/∂V)T is negative: in an isothermal expansion of a body, its pressure always decreases. This will be rigorously proved in § 21. It therefore follows from (16.10) that for all bodies
In adiabatic expansion (or contraction) of a body its entropy remains constant. The relation between the temperature, volume and pressure of the body in an adiabatic process is therefore determined by various derivatives taken at constant entropy. We shall derive formulae whereby these derivatives may be calculated from the equation of state of the body and its specific heat.
For the derivative of the temperature with respect to volume we have, changing to independent variables V, T,
or, substituting (16.3),
Similarly we find
These formulae show that, according as the thermal expansion coefficient (∂V/∂T)P is positive or negative, the temperature of the body falls or rises in an adiabatic expansion.†
Let us next calculate the adiabatic compressibility (∂V/∂P)S of the body, writing
or
The inequality Cp > Cυ therefore-implies that the adiabatic compressibility is always smaller in absolute value than the isothermal compressibility.
Using formulae (16.9) and (16.10), we can derive from (16.14) the relations
§ 17 The thermodynamic scale of temperature
We shall show how a thermodynamic scale of temperature may be constructed, at least in principle, using for this purpose an arbitrary body whose equation of state is not assumed known a priori. The problem is thus to establish by means of this body the relation T = T(τ) between the absolute scale of temperature T and some purely arbitrary scale τ defined by an arbitrarily calibrated “thermometer”.
To do this, we start from the following relation (in which all quantities refer to the body in question):
where (16.4) has been used. Since τ and T are in one-to-one relation, it does not matter whether the derivative is written for constant T or constant τ. The derivative (∂V/∂T)P may be written as
Then
or
The right-hand side involves quantities which can be measured directly as functions of the arbitrary temperature τ: (∂Q/∂P)τ is the quantity of heat which must be supplied to the body in order to maintain its temperature constant during expansion, and the derivative (∂V/∂τ)P is determined by the change in volume of the body on heating. Thus formula (17.1) gives the solution of the problem and can be used to determine the required relation T = T(τ).
Here it must be remembered that the integration of (17.1) determines log T only to within an additive constant. The temperature T is therefore determined only to within an arbitrary constant factor. This is as it should be, of course: the choice of the units of measurement of the absolute temperature remains arbitrary, which is equivalent to the presence of an arbitrary factor in the function T = T(τ).
§ 18 The Joule-Thomson process
Let us consider a process which consists in a gas (or liquid) at pressure P1 being steadily transferred to a vessel where its pressure is P2. By “steadily” we mean that the pressures P1 and P2 remain constant throughout the process. Such a process may be diagrammatically represented as a passage of the gas through a porous partition (a in Fig. 2), the constancy of pressure on either side of the partition being maintained by pistons moving inward and outward in an appropriate manner. If the holes in the partition are sufficiently small, the macroscopic flow velocity of the gas may be taken as zero. We shall also assume that the gas is thermally isolated from the external medium.
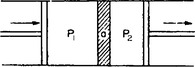
FIG. 2
This process is called a Joule-Thomson process. It must be emphasised that it is an irreversible process, as may be seen simply from the presence of the partition with very small holes, which creates a large amount of friction and destroys the velocity of the gas.
Let a quantity of gas, occupying a volume V1 at pressure P1, pass (thermally isolated) into the volume V2, the pressure becoming equal to P2. The change in energy E2−E1 of this gas is equal to the work P1V1 done on the gas to move it out of the volume V1, minus the work P2V2 done by the gas in occupying the volume V2 at pressure P2. Thus E2−E1 = P1V1−P2V2, or
that is,
Thus the heat function of the gas is conserved in a Joule-Thomson process.
The change in temperature caused by a small change of pressure in a Joule-Thomson process is given by the derivative ∂T/∂P taken with the heat function constant. We may transform this derivative to independent variables P and T:
whence, by means of formulae (14.7) and (16.7), we obtain
The change in entropy is given by the derivative (∂S/∂P)W. From the relation dW = T dS+V dP, written in the form dS = dW/T–V dP/T, we have
This quantity is always negative, as it should be: the change of a gas to a lower pressure by an irreversible Joule-Thomson process results in an increase in entropy.
We may add a few words concerning a process in which a gas originally in one of two communicating vessels expands into the other vessel; this process, of course, is not a steady one, the pressures in the two vessels varying until they become equal. When a gas expands into a vacuum in this way, its energy E is conserved. If, as a result of the expansion, the total volume is changed only slightly, the change in temperature is given by the derivative (∂T/∂V)E. On converting this derivative to independent variables V, T, we obtain the formula
The change in entropy is given by
The entropy increases on expansion, as it should.
§ 19 Maximum work
Let us consider a thermally isolated system consisting of several bodies not in thermal equilibrium with one another. While equilibrium is being established, the system may do work on some external objects. The transition to equilibrium may, however, occur in different ways, and the final equilibrium states of the system will also be different; in particular, its energy and entropy will be different.
Accordingly, the total work which can be got from a non-equilibrium system will depend on the manner in which equilibrium is established, and we may ask how the equilibrium state must be reached in order that the system should do the maximum possible amount of work. Here we are concerned with the work done because the system is not in equilibrium; that is, we must exclude any work done by a general expansion of the system, since this work could also be done by a system in equilibrium. We shall therefore assume that the total volume of the system is unchanged by the process (although it may vary during the process).
Let the original energy of the system be E0, and the energy in the equilibrium state, as a function of the entropy of the system in that state, be E(S). Since the system is thermally isolated, the work which it does is just the change in energy:
we write | R |, since R < 0 in accordance with convention if work is done by the system.
Differentiating | R | with respect to the entropy S of the final state, we have
where T is the temperature of the final state; the derivative is taken with the volume of the system in its final state constant (the same as in the initial state). We see that this derivative is negative, i.e. | R | decreases with increasing S. The entropy of a thermally isolated system cannot decrease, and the greatest possible value of | R | therefore occurs if S remains constant throughout the process.
Thus we conclude that the system does maximum work when its entropy remains constant, i.e. when the process of reaching equilibrium is reversible.
Let us determine the maximum work which can be done when a small quantity of energy is transferred between two bodies at different temperatures T1 and T2, with T2 > T1. First of all, it must be emphasised that, if the energy transfer occurred directly between the bodies on contact, no work would be done. The process would be irreversible, the entropy of the two bodies increasing by δE(1/T1−1/T2), where δE is the amount of energy transferred.
Consequently, in order to achieve a reversible transfer of energy and so maximise the work, some further body (the working medium) must be brought into the system and caused to execute a reversible cyclic process. This process must be carried out in such a way that the bodies between which direct transfer of energy occurs are at the same temperature. The working medium at temperature T2 is brought into contact with the body at that temperature and receives a certain amount of energy from it isothermally. It is then adiabatically cooled to T1, releases energy at this temperature to the body at T1, and finally is adiabatically returned to its original state. In the expansions involved in this process the working medium does work on external objects. The cyclic process just described is called a Carnot cycle.
To calculate the resulting maximum work, we first note that the working medium may be ignored, since it is returned to its initial state at the end of the process. Let the hotter body 2 lose an amount of energy − δE2 = − T2 δS2 and body 1 gain energy δE1 = T1 δS1. Since the process is reversible, the sum of the entropies of the two bodies remains constant, i.e. δS1 = − δS2. The work done is equal to the decrease in the total energy of the two bodies, i.e.
or
The ratio of the work done to the amount of energy expended is called the efficiency η. The maximum efficiency when energy is transferred from a hotter to a cooler body is, from (19.1),
A more convenient quantity is the utilisation coefficient n, defined as the ratio of the work done to the maximum work which can be obtained in given conditions. Clearly
§ 20 Maximum work done by a body in an external medium
Let us now consider a different formulation of the maximum-work problem. Let a body be in an external medium whose temperature T0 and pressure P0 differ from the temperature T and pressure P of the body. The body can do work on some object, assumed thermally isolated both from the medium and from the body. The medium, together with the body in it and the object on which work is done, forms a closed system. The volume and energy of the medium are so large that the change in these quantities due to processes involving the body does not lead to any appreciable change in the temperature and pressure of the medium, which may therefore be regarded as constant.
If the medium were absent, the work done by the body on the thermally isolated object, for a given change in state of the body (i.e. for given initial and final states) would be completely defined, and equal to the change in the energy of the body. The presence of the medium which also takes part in the process makes the result indefinite, and the question arises of the maximum work which the body can do for a given change in its state.
If a body does work on an external object in a transition from one state to another, then in the reverse transition from the second state to the first some external source of work must do work on the body. A transition in which the body does the maximum work | R |max corresponds to a reverse transition which requires the external source to do the minimum work Rmin. These must obviously be the same, so that the calculation of the one is equivalent to that of the other, and we shall speak below of the work done on the body by a thermally isolated external source of work.
During the process, the body may exchange heat and work with the medium. The work done on the body by the medium must of course be subtracted from the total work done on the body, since we are concerned only with the work done by the external source. Thus the total change ΔE in the energy of the body in some (not necessarily small) change in its state consists of three parts: the work R done on the body by the external source, the work done by the medium, and the heat gained from the medium. As already mentioned, owing to the large size of the medium its temperature and pressure may be taken as constant, and the work done by it on the body is therefore P0ΔV0, while the heat given up by it is − T0ΔS0 (the suffix zero indicates quantities pertaining to the medium, while those for the body have no suffix). Thus
Since the total volume of the medium and the body remains constant, ΔV0 = −ΔV, and the law of increase of entropy shows that ΔS + ΔS0 ≥ 0; the entropy of the thermally isolated source of work does not vary. Thus ΔS0 ≥ − ΔS. From R = ΔE−P0ΔV0+T0ΔS0 we therefore find
The equality occurs for a reversible process. Thus we again conclude that the change occurs with minimum expenditure of work, and the reverse change with maximum work, if it occurs reversibly. The value of the minimum work is
(T0 and P0, being constants, can be placed after Δ), i.e. this work is equal to the change in the quantity E−T0S+P0V. For maximum work the formula must be written with the opposite sign:
since the initial and final states are interchanged.
If the body is in an equilibrium state at every instant during the process (but not, of course, in equilibrium with the medium), then for an infinitesimal change in its state formula (20.2) may be written differently. Substituting dE = T dS−P dV in dRmin = dE−T0 dS+P0 dV, we find
Two important particular cases may be noted. If the volume and temperature of the body remain constant, the latter being equal to the temperature of the medium, (20.2) gives Rmin = Δ(E−TS), or
i.e. the minimum work is equal to the change in the free energy of the body. Secondly, if the temperature and pressure of the body are constant and equal to T0 and P0, we have
i.e. the work done by the external source is equal to the change in the thermodynamic potential of the body.
It should be emphasised that in both these particular cases the body concerned must be one not in equilibrium, so that its state is not defined by T and V (or P) alone; otherwise, the constancy of these quantities would mean that no process could occur at all. We must consider, for example, a chemical reaction in a mixture of reacting substances, a process of dissolution, or the like.
Let us now assume that a body in an external medium is left to itself and no work is done on it. Spontaneous irreversible processes will occur in the body and bring it into equilibrium. In the inequality (20.1) we must now put R = 0, and so
This means that the processes occurring in the body will cause the quantity E−T0S+P0V to decrease, and it will reach a minimum at equilibrium.
In particular, for spontaneous processes at constant temperature T = T0 and constant pressure P = P0, the thermodynamic potential Φ of the body decreases, and for processes at constant temperature T = T0 and constant volume of the body its free energy F decreases. These results have already been derived by a different approach in § 15. It may be noted that the derivation given here does not essentially assume that the temperature and volume (or pressure) of the body remain constant throughout the process: we may say that the thermodynamic potential (or free energy) of a body decreases as a result of any process for which the initial and final temperature and pressure (or volume) are the same (and equal to the temperature and pressure of the medium), even if they vary during the process.
Another thermodynamic significance may also be ascribed to the minimum work. Let St be the total entropy of the body and the medium. If the body is in equilibrium with the medium, St is a function of their total energy Et:
If the body is not in equilibrium with the medium, their total entropy differs from St(Et) for the same value of the total energy Et by some amount ΔSt < 0. In Fig. 3 the continuous line shows the function St(Et) and the vertical segment ab is − ΔSt. The horizontal segment bc is the change in the total energy when the body goes reversibly from the state of equilibrium with the medium to the state corresponding to the point b. In other words, this segment represents the minimum work which must be done by some external source to bring the body from the state of equilibrium with the medium to the state considered; the equilibrium state in question (the point c in Fig. 3) is, of course, not the same as that corresponding to the given value of Et (point a).
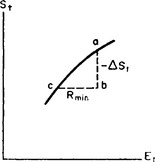
FIG. 3
Since the body is a very small part of the whole system, the processes involving it cause only a negligible relative change in the total energy and entropy. Figure 3 therefore shows that
But the derivative dEt/dSt is the equilibrium temperature of the system, i.e. the temperature T0 of the medium. Thus
This formula determines the amount by which the entropy of a closed system (body + medium) differs from its greatest possible value if the body is not in equilibrium with the medium; ΔE, ΔS and ΔV are here the differences between the energy, entropy and volume of the body and their values in a state of complete equilibrium.
§ 21 Thermodynamic inequalities
In deriving the conditions of thermal equilibrium from that of maximum entropy, we have so far considered only the first derivatives. By equating to zero the derivatives with respect to energy and volume, we have deduced in §§ 9 and 12 the equality of temperature and pressure in all parts of the body as the conditions of equilibrium. But the vanishing of the first derivatives is only a necessary condition for an extremum and does not ensure that the entropy is in fact a maximum. The determination of the sufficient conditions for a maximum involves, of course, an examination of the second derivative of the function.
Such an examination is, however, more conveniently carried out not from the condition of maximum entropy of a closed system but from another equivalent condition.† Let us consider some small but macroscopic part of the body concerned. With respect to this part, the remainder of the body may be regarded as an external medium. Then, as shown in § 20, we can state that in equilibrium the quantity
has a minimum, where E, S and V are the energy, entropy and volume of the part considered, and T0, P0 the temperature and pressure of the medium, i.e. of the remainder of the body. Clearly T0 and P0 are also the temperature and pressure of the part considered when in equilibrium.
Thus in any small deviation from equilibrium the change in the quantity E−T0S+P0V must be positive, i.e.
In other words, the minimum work which must be done to bring this part of the body from equilibrium to any neighbouring state is positive.
In what follows the equilibrium values will be implied for any coefficients appearing in the deviations of thermodynamic quantities from their equilibrium values, and the zero suffixes will therefore be omitted.
Expanding δE as a series (regarding E as a function of S and V), we have as far as the second-order terms
But ∂E/∂S = T, ∂E/∂V = −P, so that the first-order terms are T δS−P δV, and cancel when δE is substituted in (21.1). Thus we obtain the condition
If such an inequality holds for arbitrary δS and δV, two conditions must be satisfied:†
the condition (21.3) becomes T/Cυ > 0, or
i.e. the specific heat at constant volume is always positive.
The condition (21.4) may be written in terms of the Jacobian
Changing to the variables T and V, we have
Since Cυ > 0, this is equivalent to the condition
i.e. an increase in volume at constant temperature is always accompanied by a decrease in pressure.
The conditions (21.5) and (21.6) are called thermodynamic inequalities. States in which these conditions are not satisfied are unstable and cannot exist in Nature.
It has already been noted in § 16 that from the inequality (21.6) and formula (16.10) we always have Cp > Cυ. From (21.5) we can therefore conclude that
always.
The fact that Cυ and Cp are positive means that the energy is a monotonically increasing function of temperature at constant volume, and the heat function behaves similarly at constant pressure. The entropy increases monotonically with temperature at either constant volume or constant pressure.
The conditions (21.5), (21.6), which have been derived for an arbitrary small part of a body, are of course valid for the whole body also, since in equilibrium the temperatures and pressures of all parts of the body are the same. Here it is assumed that the body is homogeneous (only such bodies have been considered so far). It must be emphasised that the fulfilment of the conditions (21.5), (21.6) depends on the homogeneity of the body. We can, for example, consider a body whose particles are held together by gravitational forces. Such a body will clearly be inhomogeneous, having a higher density towards the centre, and the specific heat of the body as a whole may be less than zero, so that its temperature rises as its energy decreases. We may note that this does not contradict the result that the specific heat is positive for every small part of the body, since in these conditions the energy of the whole body is not equal to the sum of the energies of its parts; there is also the energy of the gravitational interaction between these parts.
The inequalities derived above are conditions of equilibrium, but their fulfilment is not sufficient for the equilibrium to be completely stable. There can exist states such that the entropy decreases for an infinitesimal deviation from the state and the body then returns to its initial state, whereas for a finite deviation the entropy may be greater than in the original state. After such a finite deviation the body does not return to its original state, but will tend to pass to some other equilibrium state corresponding to a maximum entropy greater than that in the original state. Accordingly, we must distinguish between metastable and stable equilibrium states. A body in a metastable state may not return to it after a sufficient deviation. Although a metastable state is stable within certain limits, the body will always leave it sooner or later for another state which is stable, corresponding to the greatest of the possible maxima of entropy. A body which is displaced from this state will always eventually return to it.
§ 22 Le Chatelier’s principle
Let us consider a closed system consisting of a body and a medium surrounding it. Let S be the total entropy of the system, and y a quantity pertaining to the body, such that the condition for S to be a maximum relative to y; i.e. ∂S/∂y = 0, signifies that the body itself is in equilibrium, though it is not necessarily in equilibrium with the medium. Also, let x be another thermodynamic quantity pertaining to the same body, such that if both ∂S/∂y = 0 and ∂S/∂x = 0 the body is not only in internal equilibrium but also in equilibrium with the medium.
In complete thermodynamic equilibrium the entropy S must be a maximum. For this, besides the conditions
the conditions
and
must be satisfied.
Let us now assume that the equilibrium of the body with the medium is destroyed by some small external interaction, the quantity x being somewhat changed and the condition X = 0 no longer satisfied; we assume that y is not directly affected by the interaction in question. Let the change in x be Δx. Then the change in X at the instant of interaction is
The change in x at constant y leads, of course, to a violation of the condition Y = 0 also, i.e. of internal equilibrium of the body. When equilibrium is again restored, the quantity X = ≡X will be
where the derivative is taken at constant Y(= 0).
To compare the two values of ΔX, using the properties of Jacobians, we have
The denominator of the second term in this expression is positive by the condition (22.3); using also (22.4), we find that
or
The inequality (22.5) or (22.6) forms the content of what is called Le Chatelier’s principle.
We shall regard the change Δx of the quantity x as a measure of the external interaction acting on the body, and ΔX as a measure of the change in properties of the body resulting from this interaction. The inequality (22.6) shows that, when the internal equilibrium of the body is restored after the external interaction which disturbed it, the value of δX is reduced. Thus Le Chatelier’s principle may be formulated as follows: an external interaction which disturbs the equilibrium brings about processes in the body which tend to reduce the effects of this interaction.
The above may be illustrated by some examples.
First of all, it is convenient to modify somewhat the definition of the quantities X and Y by using formula (20.8), according to which the change in entropy of the system (medium + body) is − Rmin/T0, where T0 is the temperature of the medium and Rmin the minimum work needed to bring the body from a state of equilibrium with the medium to the state in question. We can therefore write
For an infinitesimal change in the state of the body we have (see (20.4))
here and below all quantities without suffix relate to the body, and those with suffix 0 to the medium.
Let x be the entropy S of the body. Then X = (T−T0)/T0. The equilibrium condition X − 0 gives T = T0, i.e. the temperatures of the body and the medium are equal. The inequalities (22.5) and (22.6) become
The significance of these inequalities is as follows. The change in x (the entropy of the body) means that a quantity of heat is given to or taken from the body. This destroys the equilibrium of the body itself and, in particular, changes its temperature by (ΔT)y. The restoration of equilibrium in the body has the result that the absolute value of the change in temperature decreases, becoming (ΔT)Y=0, i.e. it is as if the result of the interaction which brings the body out of equilibrium were reduced. We can say that heating or cooling a body brings about processes in it which tend to lower or raise the temperature respectively.
Now let x be the volume V of a body. Then X = −(P−P0)/T0. In equilibrium X = 0, i.e. P = P0. The inequalities (22.5) and (22.6) give
If the body is disturbed from equilibrium by a change in its volume at constant temperature, then, in particular, its pressure is changed; the restoration of equilibrium in the body leads to a decrease in the absolute value of the change in pressure. Since a decrease in the volume of the body causes an increase in its pressure, and vice versa, we can say that decreasing or increasing the volume of a body brings about processes in it which tend to lower or raise the pressure respectively.
Later we shall meet with numerous applications of these results (to solutions, chemical reactions and so on).
It may also be noted that, if y in the inequalities (22.8) is taken to be the volume of the body, we have
since the condition Y = 0 then denotes P = P0, i.e. constant pressure. Thus we again obtain the already familiar inequalities Cp > Cυ > 0. Similarly, if in (22.10) y is taken as the entropy of a body, the condition Y = 0 implies that the temperature is constant, T = T0, and we find
another result already known.
§ 23 Nernst’s theorem
The fact that the specific heat Cυ is positive means that the energy is a monotonically increasing function of the temperature. Conversely, when the temperature falls the energy decreases monotonically, and therefore, when the temperature has its least possible value, i.e. at absolute zero, a body must be in the state of least possible energy. If we regard the energy of a body as the sum of the energies of the parts into which it may be imagined to be divided, we can say that each of these parts will also be in the state of least energy; it is clear that the minimum value of the sum must correspond to the minimum value of each term.
Thus at absolute zero any part of the body must be in a particular quantum state, the ground state. In other words, the tsatistical weights of these parts are equal to unity, and therefore so is their product, i.e. the statistical weight of the macroscopic state of the body as a whole. The entropy of the body, being the logarithm of its statistical weight, is therefore zero.
We consequently reach the important result that the entropy of any body vanishes at the absolute zero of temperature. This is called Nernst’s theorem (W. Nernst, 1906).†
It should be emphasised that this theorem is a deduction from quantum statistics, in which the concept of discrete quantum states is of essential importance. The theorem cannot be proved in purely classical statistics, where the entropy is determined only to within an arbitrary additive constant (see § 7).
Nernst’s theorem enables us to draw conclusions also concerning the behaviour of certain other thermodynamic quantities as T → 0.
For instance, it is easy to see that for T − 0 the specific heats Cp and Cυ both vanish:
This follows immediately from the definition of the specific heat in the form
When T → 0, log T → − ∞, and since S tends to a finite limit, namely zero, it is clear that the derivative tends to zero.
The thermal expansion coefficient also tends to zero:
For this derivative is equal to the derivative −(∂S/∂P)T (see (16.4)), which vanishes for T = 0, since S = 0 for T = 0 and any pressure.
The entropy usually vanishes, for T → 0, according to a power law, i.e. as S = aTn, where a is a function of pressure or volume. In this case, clearly, the specific heats and (∂V/∂T)P, (∂P/∂T)V will tend to zero in the same way (with the same value of n).
Finally, it may be seen that the difference Cp−Cυ tends to zero more rapidly than the specific heats themselves, i.e.
For let the entropy tend to zero as S ∝ Tn for T → 0. From formula (16.9) we then see that Cp−Cυ ∝ T2n+1, so that (Cp−Cυ)/Cp ∝ Tn+1; it should be borne in mind that the compressibility (∂V/∂P)T is in general finite and not zero when T = 0.
If the specific heat of a body is known for all temperatures, the entropy can be calculated by integration, and Nernst’s theorem gives the value of the constant of integration. For example, the dependence of the entropy on temperature for a given pressure is determined by
The corresponding formula for the heat function is
where W0 is the value of the heat function for T = 0. Similarly, for the thermodynamic potential Φ = W−TS we have
§ 24 The dependence of the thermodynamic quantities on the number of particles
As well as the energy and entropy, such thermodynamic quantities as F, Φ and W also have the property of additivity, as follows directly from their definitions if we bear in mind that the pressure and temperature are constant throughout a body in equilibrium. From this property we can draw certain conclusions concerning the manner in which each of these quantities depends on the number of particles in the body. Here we shall consider bodies consisting of identical particles (molecules); all the results can be immediately generalised to mixtures of different particles (see § 85).
The additivity of a quantity signifies that, when the amount of matter (and therefore the number N of particles) is changed by a given factor, the quantity is changed by the same factor. In other words, we can say that an additive thermodynamic quantity must be a homogeneous function of the first order with respect to the additive variables.
Let us express the energy of the body as a function of the entropy, volume, and number of particles. Since S and V are themselves additive, this function must be of the form
the most general homogeneous function of the first order in N, S and V.
The free energy F is a function of N, T and V. Since the temperature is constant throughout the body, and the volume is additive, a similar argument gives
In exactly the same way we have for the heat function W, expressed as a function of N, S and the pressure P,
Finally, the thermodynamic potential as a function of N, P and T is
In the foregoing discussion we have essentially regarded the number of particles as a parameter which has a given constant value for each body. We shall now formally consider N as a further independent variable. Then the expressions for the differentials of the thermodynamic potentials must include terms proportional to dN. For example, the total differential of the energy will be written
where μ denotes the partial derivative
The quantity μ is called the chemical potential of the body. Similarly we have
with the same μ. These formulae show that
i.e. the chemical potential can be obtained by differentiating any of the quantities E, W, F and Φ with respect to the number of particles, but the result is expressed in terms of different variables in each case.
Differentiating Φ in the form (24.4), we find that μ = ∂Φ/∂N = f(P, T), i.e.
Thus the chemical potential of a body (consisting of identical particles) is just its thermodynamic potential per molecule. When expressed as a function of P and T, the chemical potential is independent of N. Thus we can immediately write down for the differential of the chemical potential
where s and v are the entropy and volume per molecule.
If we consider (as we have usually done hitherto) a definite amount of matter, the number of particles in it is a given constant, while the volume is variable. Let us now take a certain volume within the body, and consider the matter enclosed therein; the number of particles N will now be variable, and the volume V constant. Then, for example, equation (24.8) reduces to
Here the independent variables are T and N. We may define a thermodynamic potential such that the second independent variable is μ, not N. To do so, we substitute μ, dN = d(μN)−N dμ, obtaining
But μN = Φ, and F−Φ = −PV. Thus the new thermodynamic potential (denoted by Ω) is just
and
The number of particles is obtained by differentiating Ω with respect to the chemical potential at constant temperature and volume:
In the same way as we proved the equality of small changes in E, W, F and Φ (with the appropriate pairs of quantities constant), we can easily show that the change (δΩ)T, μ, V at constant T, μ, V has the same property:
These equations refine and extend the theorem of small increments (15.12).
Finally, as in §§ 15 and 20 for the free energy and the thermodynamic potential, we may show that the work in a reversible process occurring at constant T, V and μ is equal to the change in the potential Ω. In a state of thermal equilibrium the potential Ω is a minimum with respect to any change of state at constant T, V, μ.
§ 25 Equilibrium of a body in an external field
Let us consider a body in an external field which is constant in time. The different parts of the body are in different conditions, and the body will therefore be inhomogeneous. One of the conditions of equilibrium of such a body is again that the temperature should be constant throughout it, but the pressure will now vary from point to point.
To derive the second condition of equilibrium, let us consider two adjoining volumes in the body and maximise their entropy S = S1 + S2 when the remainder of the body is in a fixed state. One necessary condition for a maximum is that the derivative ∂S/∂N1 should be zero. Since the total number of particles N1 + N2 in these two parts of the body is regarded as constant, we have
The equation dE = T dS + μ dN, written in the form
shows that the derivative ∂S/∂N for constant E and V is − μ/T. Thus μ1/T1 = μ2/T2. But in equilibrium T1 = T2, so that μ1 = μ2. We therefore conclude that in equilibrium in an external field, in addition to the constancy of temperature, we must have
i.e. the chemical potential of every part of the body must be the same. The chemical potential of each part is a function of its temperature and pressure, as well as of the parameters which define the external field. If there is no field, the constancy of μ and T necessarily implies that of the pressure.
In a gravitational field the potential energy u of a molecule is a function only of the coordinates x, y, z of its centre of gravity (and not of the arrangement of the atoms within the molecule). In this case the change in the thermodynamic quantities for the body amounts to adding to its energy the potential energy of the molecules in the field. In particular, the chemical potential (the thermodynamic potential per molecule) has the form μ = μ0+u(x, y, z), where μ0(P, T) is the chemical potential in the absence of the field. Thus the condition of equilibrium in a gravitational field may be written
In particular, in a uniform gravitational field u = mgz (where m is the mass of a molecule, g the acceleration due to gravity, and z the vertical coordinate). Differentiating equation (25.2) with respect to the coordinate z at constant temperature, we have v dP = − mg dz, where v = (∂μ0/∂P)T is the specific volume. For small changes in pressure, v may be regarded as constant. Substituting the density 
= m/v and integrating, we obtain
the customary formula for the hydrostatic pressure in an incompressible fluid.
§ 26 Rotating bodies
In a state of thermal equilibrium, as we have seen in § 10, only a uniform translational motion and a uniform rotation of a body as a whole are possible. The uniform translational motion needs no special treatment, since by Galileo’s relativity principle it has no effect on the mechanical properties of the body, nor therefore on its thermodynamic properties, and the thermodynamic quantities are unchanged except that the energy of the body is increased by its kinetic energy.
Let us consider a body in uniform rotation round a fixed axis with angular velocity Ω. Let E(p, q) be the energy of the body in a fixed coordinate system and E’(p, q) the energy in a coordinate system rotating with the body. We know from mechanics that these quantities are related by
where M(p, q) is the angular momentum of the body.†
Thus the energy E’(p, q) depends on the angular velocity Ω as a parameter, and
Averaging this equation over the statistical distribution and using formula (11.3), we obtain
where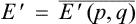 
, 
are the mean (thermodynamic) energy and angular momentum of the body.
From this relation we can write down the differential of the energy of a rotating body of given volume:
Similarly, for the free energy F’ = E’−TS (in the rotating coordinate system) we have
Averaging equation (26.1) gives
Differentiating this equation and substituting (26.3), we obtain the differential of the energy in the fixed coordinate system:
Correspondingly, for the free energy F = E−TS
Thus in these relations the independent variable is not the angular velocity but the angular momentum, and
As we know from mechanics, a uniform rotation is in a certain sense equivalent to the presence of two fields of force, centrifugal and Coriolis. The centrifugal forces are proportional to the size of the body, as they involve the distance from the axis of rotation; the Coriolis forces are independent of the size of the body. For this reason the effect of the Coriolis forces on the thermodynamic properties of a rotating macroscopic body is entirely negligible in comparison with that of the centrifugal forces, and the former can usually be neglected.† The condition of thermal equilibrium of a rotating body is therefore obtained by simply substituting for u(x, y, z) in (25.2) the centrifugal energy of the particles:
where μ0 is the chemical potential of the body at rest, m the mass of a molecule, and r the distance from the axis of rotation.
For the same reason, the total energy E of a rotating body may be written as the sum of its internal energy (here denoted by Ein) and its kinetic energy of rotation:
where I is the moment of inertia of the body with respect to the axis of rotation. It should be remembered that rotation in general changes the distribution of mass in the body, and so the moment of inertia and internal energy of the body are themselves in general functions of Ω (or of M). They may be regarded as constants independent of Ω only when the rotation is sufficiently slow.
Let us consider an isolated uniformly rotating solid with a given mass distribution. Since the entropy of a body is a function of its internal energy, we have in this case S = S(E−M2/21). Because the body is a closed system, its total energy and angular momentum are conserved, and the entropy must have the maximum value possible for the given M and E. We therefore conclude that the equilibrium rotation of the body takes place about the axis with respect to which the moment of inertia has the greatest possible value. This assumes that the axis of rotation is necessarily a principal axis of inertia of the body, but the latter result is evident: if the body rotates about an axis other than a principal axis of inertia, then, as we know from mechanics, the axis of rotation will itself precess in space, and the rotation will be non-uniform, and therefore not an equilibrium rotation.
§ 27 Thermodynamic relations in the relativistic region
Relativistic mechanics leads to a number of changes in the usual thermodynamic relations. Here we shall discuss the most interesting of these changes.
If the microscopic motion of the particles forming a body becomes relativistic, the general thermodynamic relations are unchanged, but there is an important inequality between the pressure and energy of the body:
where E is the energy of the body including the rest energy of the particles in it.†
The changes caused by the general theory of relativity in the conditions of thermal equilibrium, taking account of the gravitational field of the body itself, are of fundamental importance. Let us consider a macroscopic body at rest; its gravitational field is, of course, constant. In a constant gravitational field we must distinguish the conserved energy E0 of any small part of the body from the energy E measured by an observer situated at a given point. These two quantities are related by
where g00 is the time component of the metric tensor; see Fields, § 88, formula (88.9) with v = 0, mc2 = E. But, from the sense of the proof given in § 9 that the temperature is constant throughout a body in equilibrium, it is clear that the quantity obtained by differentiating the entropy with respect to the conserved energy E0 must be constant. The temperature T measured by an observer situated at a given point in space is, however, obtained by differentiating the entropy with respect to the energy E, and will therefore be different at different points in the body.
To derive a quantitative relation, we note that the entropy, by definition, depends only on the internal state of the body and so is unchanged by the presence of a gravitational field (provided that this field does not affect the internal properties of the body, a condition which is always satisfied in practice). The derivative with respect to entropy of the conserved energy E0 is therefore T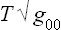
, and so one of the conditions of thermal equilibrium is that
throughout the body.
A similar change occurs in the second condition of equilibrium, the constancy of the chemical potential. The latter is defined as the derivative of the energy with respect to the number of particles. Since this number is of course unaffected by a gravitational field, we have for the chemical potential measured at any given point a relation of the same kind as for the temperature:
We may note that the relations (27.2), (27.3) may be written
which enable us to consider the body not only in the frame of reference in which it is at rest but also in those where it is moving (rotating as a whole). The derivative dx0/ds must be taken along the world line described by the point considered in the body.
In a weak (Newtonian) gravitational field, g00 = 1 + 2φ/c2, where φ is the gravitational potential (see Fields, § 87). Substituting this expression in (27.2) and taking the square root, we have to the same approximation
Since φ < 0, this shows that in equilibrium the temperature is higher at points in the body where | φ | is greater, i.e. within the body. In the limit of non-relativistic mechanics (c → ∞), (27.5) becomes T = constant, as it should.
We can similarly transform the condition (27.3), bearing in mind that the relativistic chemical potential, in the limit of classical mechanics, does not directly become the ordinary (non-relativistic) expression for the chemical potential in the absence of a field, which we now denote by μ0, but μ0+mc2, where mc2 is the rest energy of a particle of the body. Thus we have
so that the condition (27.3) becomes
this agrees with (25.2), as it should.
Finally, we may mention a useful relation which follows immediately from the conditions (27.2) and (27.3). Dividing one by the other, we find that μ/T = constant, and hence
From (24.12), at constant volume (equal to unity) we have
where S and N are the entropy and number of particles in unit volume of the body. Substituting dT = (T/μ) dμ and noting that μN+ ST = Φ + ST = ε + P, where ε is the energy per unit volume, gives†
†Fluctuations of thermodynamic quantities will be discussed in a separate chapter (Chapter XII).
†For reference, we may also give the conversion factor between degrees and electron-volts:
‡The fact that the entropy of a body is a function only of its internal energy follows at once from Galileo’s relativity principle; the number of quantum states, and therefore the statistical weight (whose logarithm is the entropy), must be the same in all inertial frames of reference, and in particular that in which the body is at rest.
†The derivative with respect to a vector is to be understood as another vector whose components are equal to the derivatives with respect to the components of the first vector.
‡To avoid misunderstanding, an important exception to this rule should be noted: superfluid liquid helium cannot rotate as a whole. This effect will be discussed elsewhere in the Course of Theoretical Physics. Here we shall only mention that the proof given above is invalid in that case, because the velocity distribution is subject to a further condition (the superfluid flow is a potential flow) and the entropy maximum is to be sought under this condition.
†The temperature T = 0 (absolute zero) corresponds to −273.15°C.
†In practice this may be a very weak condition, so that the “slow” adiabatic process may be quite a “fast” one. For example, in the expansion of a gas, say in a cylinder with a piston moving outwards, the speed of the piston need be small only compared with the velocity of sound in the gas, i.e. it may in practice be very large.
In general textbooks on physics an adiabatic expansion (or compression) is often defined as one which is “sufficiently rapid”. This refers to a different aspect of the problem: the process must occur so rapidly that the body cannot exchange heat with the surrounding medium. Thus the condition in question is one which will in practice ensure that the body is thermally isolated, and the condition of slowness compared with processes leading to the establishment of equilibrium is tacitly assumed satisfied.
†In so far as we neglect the energy of interaction of these parts; this is not permissible if we are interested in effects arising from the presence of interfaces between different bodies. Chapter XV deals with this topic.
†These statements are applicable in practice to liquids and gases but not to solids. A change in shape (deformation) of a solid involves the doing of work, so that the energy of the body is changed. This is because the deformed state of the solid is, strictly speaking, an incomplete thermodynamic equilibrium (but the relaxation time for the establishment of complete equilibrium is so long that in many respects the deformed body behaves as if in equilibrium).
†These are defined in § 21. Negative pressures are further discussed in the footnote following (83.1).
†In this sense the notation dR and dQ is not quite precise, and we therefore avoid it as far as possible.
†An example is the Joule-Thomson process (see § 18) with a small change in pressure.
‡Also called the enthalpy or heat content.
†In Western literature, the functions F and Φ are often called respectively the Helmholtz free energy and the Gibbs free energy.
†It should be remembered that in both cases the processes in question are those (such as chemical reactions) for which the body is not in equilibrium, so that its state is not uniquely defined by the temperature and the volume (or pressure).
†The Jacobian ∂(u, υ)/∂(x, y) is defined as the determinant
It clearly has the following properties:
The following relations also hold:
†In § 21 it will be shown rigorously that Cυ is always positive, and therefore so is Cp.
†As regards the dependence of the entropy on the momenta of macroscopic motion, we have already investigated the conditions to be imposed on both the first and the second derivatives (§ 10), obtaining in this way the conditions that internal macroscopic motions in the body be absent and that the temperature be positive.
†The special case where the equality sign holds in (21.4) will be discussed in § 152.
†To avoid misunderstandings we should emphasise that this refers to the temperature tending to zero with other conditions remaining unchanged−say at constant volume, or at constant pressure. If, on the other hand, the temperature of a gas tends to zero while its density decreases without limit, for example, the entropy need not tend to zero.
†See Mechanics, § 39. Although the derivation of formula (39.13) is based on classical mechanics, in quantum theory exactly the same relations apply to the operators of the corresponding quantities. Hence all the thermodynamic relations derived below are independent of which mechanics describes the motion of the particles in the body.
†It may be shown that in classical statistics the Coriolis forces do not affect the statistical properties of the body; see § 34.
†See Fields, § 35. It should be mentioned, however, that there is as yet no general proof of this inequality valid for all types of interaction (not only electromagnetic) which exist between particles in Nature.
†In the non-relativistic case, putting μ ≅ mc2, ε ≅ c2 » P (where is the density), we get dμ − v dP with v = m/ the volume per particle; this is as it should be for T = constant.