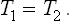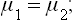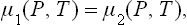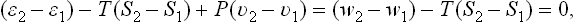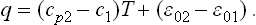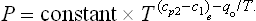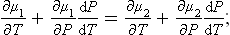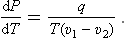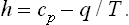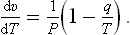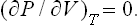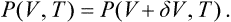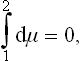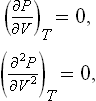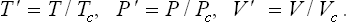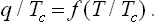PHASE EQUILIBRIUM
Publisher Summary
The equilibrium state of a homogeneous body is determined by specifying any two thermodynamic quantities. For a given volume and energy in thermal equilibrium, the body is not homogeneous, but separates into two homogeneous parts in contact, which are in different states. Such states of matter that can exist simultaneously in equilibrium with one another and in contact are described as different phases. The change from one phase to another is accompanied by the evolution or absorption of a certain quantity of heat, called the latent heat of transition or the heat of transition. According to the conditions of equilibrium, such a transition occurs at constant pressure and temperature. However, in a process occurring at constant pressure, the quantity of heat absorbed by the body is equal to the change in its heat function. The phase equilibrium curve may terminate at a certain point, called the critical point, where the corresponding temperature and pressure are the critical temperature and the critical pressure.
§ 81 Conditions of phase equilibrium
THE (equilibrium) state of a homogeneous body is determined by specifying any two thermodynamic quantities, for example the volume V and the energy E. There is, however, no reason to suppose that for every given pair of values of V and E the state of the body corresponding to thermal equilibrium will be homogeneous. It may be that for a given volume and energy in thermal equilibrium the body is not homogeneous, but separates into two homogeneous parts in contact which are in different states.
Such states of matter which can exist simultaneously in equilibrium with one another and in contact are described as different phases.
Let us write down the conditions for equilibrium between two phases. First of all, as for any bodies in equilibrium, the temperatures T1 and T2 of the two phases must be equal:
The pressures in the two phases must also be equal:
since the forces exerted by the two phases on each other at their surface of contact must be equal and opposite. Finally, the chemical potentials of the two phases must be equal:
this condition is derived for the two phases in exactly the same way as in § 25 for any two adjoining regions of a body. If the potentials are expressed as functions of pressure and temperature, and the common temperature and pressure are denoted by T and P, we have
whence the pressure and temperature of phases in equilibrium can be expressed as functions of each other. Thus two phases can not be in equilibrium with each other at all pressures and temperatures; when one of these is given, the other is completely determined.
If the pressure and temperature are plotted as coordinates, the points at which phase equilibrium is possible will lie on a curve (the phase equilibrium curve), and the points lying on either side of the curve will represent homogeneous states of the body. When the state of the body varies along a line which intersects the equilibrium curve, the phases separate at the point of intersection and the body then changes to the other phase. It may be noted that, when the state of the body changes slowly, it may sometimes remain homogeneous even when the phases should separate in complete equilibrium. Examples are supercooled vapours and superheated liquids, but such states are only metastable.
If the equilibrium of phases is plotted in a diagram with temperature and volume (of a fixed quantity of matter) as coordinates, then the states in which two phases exist simultaneously will occupy a whole region of the plane, and not simply a curve. This difference from the (P, T) diagram arises because the volume V, unlike the pressure, is not the same for the two phases. The resulting diagram is of the kind shown in Fig. 12. Points in the regions I and II on either side of the hatched area correspond to homogeneous first and second phases. The hatched area represents states in which the two phases are in equilibrium: at any point a the phases I and II are in equilibrium, with specific volumes given by the abscissae of the points 1 and 2 which lie on a horizontal line through a. It is easily deduced directly from the mass balance that the quantities of phases I and II are inversely proportional to the lengths of the segments a1 and a2; this is called the lever rule.
FIG. 12
In a similar way to the conditions for equilibrium of two phases, the equilibrium of three phases of the same substance is governed by the equations
If the common values of the pressure and temperature of the three phases are again denoted by P and T we have the conditions
These give two equations in the two unknowns P and T and their solutions are specific pairs of values of P and T. The states in which three phases are simultaneously present (called triple points) in the (P, T) diagram are represented by isolated points which are the points of intersection of the equilibrium curves of each pair of phases (Fig. 13, where regions I, II, III are those of the three homogeneous phases). The equilibrium of more than three phases of the same substance is clearly impossible.
FIG. 13
In the (T, V) diagram the neighbourhood of the triple point has the appearance shown in Fig. 14, where the hatched areas are those of equilibrium of two phases; the specific volumes of the three phases in equilibrium at the triple point (at the temperature Ttr) are given by the abscissae of the points 1, 2, 3.
FIG. 14
The change from one phase to another is accompanied by the evolution or absorption of a certain quantity of heat, called the latent heat of transition or simply the heat of transition. According to the conditions of equilibrium such a transition occurs at constant pressure and temperature. But in a process occurring at constant pressure the quantity of heat absorbed by the body is equal to the change in its heat function. The heat of transition q per molecule is therefore
where w1 and w2 are the heat functions per molecule of the two phases. The quantity q is positive if heat is absorbed by the body in changing from the first to the second phase, and negative if heat is evolved.
Since, for bodies consisting of a single substance, μ is the thermodynamic potential per molecule, we can write μ = 
−Ts+Pv (where , s, v are the molecular energy, entropy and volume). The condition μ1 = μ2 therefore gives
where T and P are the temperature and pressure of both phases; hence
We may note that this formula also follows directly from q = ∫ T ds with T constant; the latter formula is applicable here, since the transition is reversible: the two phases remain in equilibrium during the transition process.
Let the two curves in Fig. 15 represent the chemical potentials of the two phases as functions of temperature (at a given pressure). The point of intersection of the two curves gives the temperature T0 for which (at the given pressure) the two phases can exist in equilibrium. At any other temperature only one or the other phase can exist. It is easy to see that at temperatures below T0 the first phase exists, i.e. is stable, and at temperatures above T0 the second phase. This follows because the stable state is the one where μ is smaller, since the thermodynamic potential tends to a minimum for given P and T. At the point of intersection of the two curves, the derivative ∂μ1/∂T is greater than ∂μ2/∂T, i.e. the entropy of the first phase, s1 = −∂μ1/∂T, is less than that of the second phase, s2 = —∂μ2/∂T. The heat of transition q = T(s2—s1) is therefore positive. Thus we conclude that, if the body goes from one phase to another when the temperature is raised, heat is absorbed in the process. This result could also be derived from Le Chatelier’s principle.
FIG. 15
PROBLEMS
PROBLEM 1
Determine the temperature dependence of the saturated vapour pressure above a solid. The vapour is regarded as an ideal gas, and both the gas and the solid have constant specific heats.
SOLUTION
The chemical potential of the vapour is given by formula (43.3) and that of the solid by (65.6); since the saturated vapour pressure is relatively small, the quantity PV may be neglected for the solid, and ϕ taken as equal to F. Equating the two expressions, we find
where the suffix 1 refers to the solid and 2 to the vapour.
In the same approximation, the heat function of the solid may be taken as equal to its energy; the heat of transition (heat of sublimation) q = w2—w1 is
In particular, for T = 0 the heat of transition is q0 = 02—01, so that we can write
SOLUTION
The rate of evaporation into a vacuum is determined by the number of particles which leave unit surface area of the body per unit time. Let us consider a body in equilibrium with its saturated vapour. Then the number of particles leaving the surface is equal to the number which strike and “adhere to” this surface in the same time, i.e. 
, where P0 = P0(T) is the saturated vapour pressure, and R a mean reflection coefficient for gas particles colliding with the surface (see (39.2)). If P0 is not too large, the number of particles leaving the surface of the body is independent of whether there is vapour in the surrounding space, so that the above expression gives the required rate of evaporation into a vacuum.
§ 82 The Clapeyron-Clausius formula
Let us differentiate both sides of the equilibrium condition μ1(P, T) = μ2(P, T) with respect to temperature, bearing in mind, of course, that the pressure P is not an independent variable but a function of temperature determined by this same equation. We therefore write
since (∂μ/∂T)P = —s, (∂μ/∂P)T = v (see (24.12)), this gives
where s1, v1, s2, v2 are the molecular entropies and volumes of the two phases.
In this formula the difference s1—s2 may conveniently be expressed in terms of the heat of transition from one phase to the other. Substituting q = T(s2—s1), we obtain the Clapeyron-Clausius formula:
This gives the change in the pressure of phases in equilibrium when the temperature changes or, in other words, the change in pressure with temperature along the phase equilibrium curve. The same formula written as
gives the change in the temperature of the transition between phases (e.g. freezing point or boiling point) when the pressure changes. Since the molecular volume of the gas is always greater than that of the liquid, and heat is absorbed in the passage from liquid to vapour, it follows that the boiling point always rises when the pressure increases (dT/dP > 0). The freezing point may rise or fall with increasing pressure, according as the volume increases or decreases on melting.†
All these consequences of formula (82.2) are in full agreement with Le Chatelier’s principle. Let us consider, for example, a liquid in equilibrium with its saturated vapour. If the pressure is increased, the boiling point must rise, and so some of the vapour will become liquid; this in turn will cause a decrease in pressure, so that the system acts as if to oppose the interaction which disturbs its equilibrium.
Let us consider the particular case of formula (82.2) which relates to equilibrium between a solid or liquid and its vapour. Then formula (82.2) determines the change in the saturated vapour pressure with temperature.
The volume of a gas is usually much greater than that of a liquid or solid containing the same number of particles. We can therefore neglect the volume v1 in (82.2) in comparison with v2 (the second phase being taken to be a gas), i.e. write dP/dT = q/Tv2. Regarding the vapour as an ideal gas, we can express its volume in terms of the pressure and temperature by v2 = T/P; then dP/dT = qP/T2, or
We may note that, in temperature intervals over which the heat of transition may be regarded as constant, the saturated vapour pressure varies exponentially with the temperature (∝ e−q/T).
PROBLEMS
PROBLEM 1
Determine the specific heat of a vapour along the equilibrium curve of the liquid and its saturated vapour (i.e. the specific heat for a process in which the liquid is always in equilibrium with its saturated vapour). The vapour is regarded as an ideal gas.
SOLUTION
The required specific heat h = T ds/dT, where ds/dT is the derivative along the equilibrium curve:
Substituting the expression given by (82.3) for dP/dT, and v = T/P, we find
At low temperatures, h is negative, i.e. if heat is removed in such a way that the vapour is always in equilibrium with the liquid, its temperature can increase.
PROBLEM 2
Determine the change in the volume of a vapour with temperature in a process where the vapour is always in equilibrium with the liquid (i.e. along the equilibrium curve of the liquid and its vapour).
SOLUTION
We have to determine the derivative dv/dT along the equilibrium curve:
Substituting from (82.3), and v = T/P, we find
At low temperatures dv/dT < 0, i.e. the vapour volume decreases with increasing temperature in the process considered.
§ 83 The critical point
The phase equilibrium curve (in the PT-plane) may terminate at a certain point (Fig. 16), called the critical point; the corresponding temperature and pressure are the critical temperature and the critical pressure. At temperatures above Tc and pressures higher than Pc, no difference of phases exists, the substance is always homogeneous, and we can say that at the critical point the two phases become identical. The concept of the critical point was first used by D. I. Mendeleev (1860).
FIG. 16
In the coordinates T, V, when there is a critical point, the equilibrium diagram appears as in Fig. 17. As the temperature approaches its critical value, the specific volumes of the phases in equilibrium become closer, and at the critical point (K in Fig. 17) they coincide. The diagram in the coordinates P, V has a similar form.
FIG. 17
When there is a critical point, a continuous transition can be effected between any two states of the substance without its ever separating into two phases. To achieve this, the state must be varied along a curve which passes round the critical point and nowhere intersects the equilibrium curve. In this sense, when there is a critical point, the concept of different phases is itself arbitrary, and it is not possible to say in every case which states have one phase and which have the other. Strictly speaking, there can be said to be two phases only when they exist simultaneously and in contact—that is, at points lying on the equilibrium curve.
It is clear that the critical point can exist only for phases such that the difference between them is purely quantitative, for example a liquid and a gas differing only in the degree of interaction between the molecules.
On the other hand, such phases as a liquid and a solid (crystal), or different crystal modifications of a substance, are qualitatively different, since they have different internal symmetry. It is clear that we can say only that a particular symmetry property (symmetry element) exists or does not exist; it can appear or disappear only as a whole, not gradually. In each state the body will have one symmetry or the other, and so we can always say to which of the two phases it belongs. The critical point therefore cannot exist for such phases, and the equilibrium curve must either go to infinity or terminate by intersecting the equilibrium curves of other phases.
An ordinary phase transition point is not a mathematical singularity of the thermodynamic quantities of the substance. For each of the phases can exist (though in a metastable state) beyond the transition point; the thermodynamic inequalities are not violated at that point. At the transition point the chemical potentials of the two phases are equal: μ1(P, T) = μ2(P, T); but this point has no special property with respect to either one of the functions μ1(P, T) and μ2(P, T).†
Let us plot in the PV-plane an isotherm of the liquid and gas, i.e. the curve of P as a function of V in an isothermal expansion of a homogeneous body (abc and def in Fig. 18). According to the thermodynamic inequality (∂P/∂V)T < 0, P is a decreasing function of V. This slope of the isotherms must continue for some distance beyond their intersections (b and e) with the liquid-gas equilibrium curve; the segments be and ed of the isotherms correspond to metastable superheated liquid and supercooled vapour, in which the thermodynamic inequalities are still satisfied. (A complete-equilibrium isothermal change of state between the points b and e corresponds, of course, to the horizontal segment be, on which separation into two phases occurs.) If we use the fact that the points b and e have the same ordinate P, it is clear that the two parts of the isotherm cannot pass continuously into each other; there must be a discontinuity between them. The isotherms terminate at points (c and d) where the thermodynamic inequality ceases to hold, i.e.
FIG. 18
By constructing the locus of the points of termination of the isotherms of the liquid and gas, we obtain a curve AKB on which the thermodynamic inequalities are violated (for a homogeneous body), and which is the boundary of a region in which the body can never exist in a homogeneous state. The regions between this curve and the phase equilibrium curve correspond to superheated liquid and supercooled vapour.† It is evident that at the critical point the two curves must touch.
Of the points lying on the curve AKB itself, only the critical point K corresponds to an actually existing state of the homogeneous body; this is the only point where the curve reaches the region of stable homogeneous states.
It is worth mentioning that the condition (83.1) at the critical point can also be derived from the following simple considerations. Near the critical point, the specific volumes of the liquid and the vapour are almost the same; denoting them by V and V + ΔV, we can write the condition for equal pressures of the two phases as
Expanding the right-hand side in powers of ΔV and dividing by the small but finite quantity ΔV, we have
Hence we see that, when ΔV tends to zero, i.e. at the critical point, (∂P/∂V)T must tend to zero.
In contrast to the ordinary phase-equilibrium points, the critical point is a mathematical singularity of the thermodynamic functions of the substance (and the same applies to the whole curve AKB which bounds the region where homogeneous states of the body exist). The nature of this singularity and the behaviour of matter near the critical point will be discussed in § 153.
§ 84 The law of corresponding states
Van der Waals’ interpolation formula for the equation of state,
is in qualitative agreement with the properties of the liquid-vapour transition which have been described in the preceding sections. The isotherms determined by this equation are shown in Fig. 19. Curves passing above the critical point K represent monotonically decreasing functions P(V) for T > Tc. The isotherm that passes through the critical point has an inflexion there. At temperatures T < Tc, each isotherm has a minimum and a maximum, and between them is a section with (∂P/∂V)T > 0; these sections (shown by the broken lines in Fig. 19) do not correspond to any homogeneous states of matter that actually exist in Nature.
FIG. 19
As has been explained in § 83, a straight horizontal segment intersecting the isotherm corresponds to the equilibrium liquid-gas transition. The level at which this segment must be drawn is determined by the phase equilibrium condition μ1 = μ2, which we write as
the integral being taken along the path of the transition from a state of one phase to a state of the other phase. Integrating along the isotherm, we have d/μ, = v dP, and hence
Geometrically, this condition signifies that the areas shown hatched in Fig. 19 for one isotherm are equal (Maxwell’s rule).
The critical temperature, critical pressure and critical volume can be expressed in terms of the parameters a and b which appear in van der Waals’ equation. To do this, we differentiate (84.1) and put
which determine the point of inflexion on the isotherm. These equations with (84.1) give
We now use the reduced temperature, pressure and volume,
In terms of these quantities, van der Waals’ equation becomes
It contains only V′, P′ and T′, and not quantities pertaining to a given substance. equation 84.5 is therefore the equation of state for all bodies to which van der Waals’ equation is applicable. The states of two bodies for which their values of T′, P′, V′ are equal are called corresponding states (clearly the critical states of all bodies are corresponding states). It follows from (84.5) that, if two bodies have equal values of two of the three quantities T′, P′, V′, then the values of the third quantity are also equal, i.e. they are in corresponding states (the law of corresponding states).
The “reduced” isotherms P’ = P′(V′) given by equation 84.5 are the same for all substances. The positions of the straight segments which give the liquid-gas transition points are therefore also the same. We can therefore conclude that for equal reduced temperatures the following quantities must be the same for all substances: (1) the reduced saturated vapour pressure, (2) the reduced specific volume of the saturated vapour, (3) the reduced specific volume of the liquid in equilibrium with the saturated vapour.
The law of corresponding states can also be applied to the heat of transition from the liquid to the gaseous state. Here the “reduced heat of evaporation” must be represented by a dimensionless quantity, q/Tc. We can therefore write†
In conclusion, we may note that the law of corresponding states does not apply only to van der Waals’ equation. The parameters of a specific substance disappear when reduced quantities are used in any equation of state containing only two such parameters. The law of corresponding states, taken as a general theorem not pertaining to any specific form of the equation of state, is somewhat more accurate than van der Waals’ equation, but its applicability is in general very restricted.
†The liquid helium isotope He3 is an exception. Its heat of fusion is negative over a certain temperature range.
†It must be noted, however, that there is some degree of arbitrariness in these statements, due to an indeterminateness of μ(P, T) in the region of metastability. The metastable state is one of partial equilibrium, having a certain relaxation time, in this case for the process of formation of nuclei of a new phase (see § 162). The thermodynamic functions in such a state can therefore be defined only without taking account of these processes, and they cannot be regarded as the analytic continuation of the functions from the region of stability corresponding to the complete equilibrium states of the substance.
†The segment of the isotherm that corresponds to superheated liquid (bc in Fig. 18) may lie partly below the abscissa axis. Thus a superheated liquid may have a negative pressure. Such a liquid exerts an inward force on its boundary surface. Thus the pressure is not necessarily positive, and there can exist in Nature states (though only metastable ones) of a body with negative pressures, as already mentioned in § 12.
†At temperatures considerably below the critical temperature, the ratio q/Tc is approximately 10 (where q is the molecular heat of evaporation).