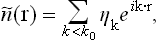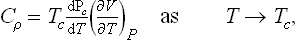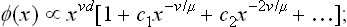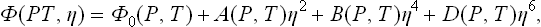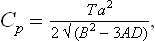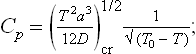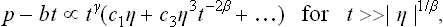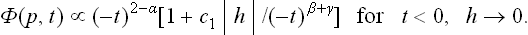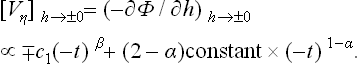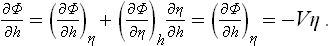PHASE TRANSITIONS OF THE SECOND KIND AND CRITICAL PHENOMENA
Publisher Summary
The transition between phases of different symmetry cannot occur in a continuous manner as is possible for a liquid and a gas. In every state, the body has either one symmetry or the other; therefore, it could be assigned to one of the two phases. The transition between different crystal modifications is effected by the means of a phase transition in which there is a sudden rearrangement of the crystal lattice and the state of the body changes discontinuously. To describe quantitatively the change in the structure of the body when it passes through the phase transition point, the order parameter can be defined in such a way that it takes nonzero values in the unsymmetrical phase and is zero in the symmetrical phase. The existing theory of phase transitions of the second kind is based on certain hypotheses that are plausible. It rests on the confirmation of these hypotheses by experimental results and by numerical calculations for certain simple models.
§ 142 Phase transitions of the second kind
IT HAS already been mentioned in § 83 that the transition between phases of different symmetry (crystal and liquid; different crystal modifications) cannot occur in a continuous manner such as is possible for a liquid and a gas. In every state the body has either one symmetry or the other, and therefore we can always assign it to one of the two phases.
The transition between different crystal modifications is usually effected by means of a phase transition in which there is a sudden rearrangement of the crystal lattice and the state of the body changes discontinuously. As well as such discontinuous transitions, however, another type of transition involving a change of symmetry is also possible.
To elucidate the nature of these transitions, let us consider a specific example. At high temperatures, BaTiO3 has a cubic lattice whose unit cell is as shown in FIG. 60 (the barium atoms are at the vertices, the oxygen atoms at the centres of the faces, and the titanium atoms at the centres of the cells). As the temperature decreases below a certain value, the titanium and oxygen atoms begin to move relative to the barium atoms parallel to an edge of the cube. It is clear that, as soon as this movement begins, the symmetry of the lattice is affected, and it becomes tetragonal instead of cubic.

FIG. 60
This example is typical in that there is no discontinuous change in state of the body. The configuration of atoms in the crystal† changes continuously. However, an arbitrarily small displacement of the atoms from their original symmetrical positions is sufficient to change the symmetry of the lattice. The resulting transition from one crystal modification to another is called a phase transition of the second kind, in contrast to ordinary phase transitions, which in this case are said to be of the first kind.‡
Thus a phase transition of the second kind is continuous in the sense that the state of the body changes continuously. It should be emphasised, however, that the symmetry, of course, changes discontinuously at the transition point, and at any instant we can say to which of the two phases the body belongs. But whereas at a phase transition point of the first kind bodies in two different states are in equilibrium, the states of the two phases are the same at a transition point of the second kind.
As well as cases where the change in symmetry of the body occurs by a displacement of the atoms (as in the example given above), the change in symmetry in a phase transition of the second kind may result from a change in the ordering of the crystal. It has already been mentioned in § 64 that the concept of ordering arises if the number of lattice points that can be occupied by atoms of a given kind exceeds the number of such atoms. We shall use the word “own” for the places occupied by atoms of the kind in question in a completely ordered crystal, in contrast to the “other” places which are taken by some of the atoms when the crystal becomes disordered. In many cases, which will be of interest in connection with transitions of the second kind, it is found that the “own” and “other” lattice sites are geometrically identical and differ only in that they have different probabilities of containing atoms of the kind in question.§ If now these probabilities become equal (they will not be unity, of course), all such sites become equivalent, and therefore new symmetry elements appear, i.e. the symmetry of the lattice is increased. Such a crystal will be said to be disordered.
The foregoing may be illustrated by an example. The completely ordered alloy CuZn has a cubic lattice with the zinc atoms at the vertices, say, and the copper atoms at the centres of the cubic cells (Fig. 61a; a simple cubic Bravais lattice). When the alloy becomes disordered, copper and zinc atoms change places, i.e. non-zero probabilities of finding atoms of either kind exist at every lattice site. Until the probabilities of finding copper (or zinc) atoms at the vertices and at the centres of the cells become equal (that is, while the crystal is not completely ordered), these sites remain non-equivalent, and the symmetry of the lattice is unchanged. But when the probabilities become equal, all sites become equivalent, and the symmetry of the crystal is raised: a new lattice vector appears, from a vertex to the centre of a cell, and the crystal acquires a body-centred cubic Bravais lattice (Fig. 61b).†
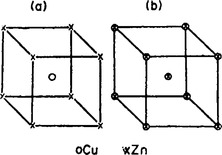
FIG. 61
So far we have discussed only transitions between different crystal modifications, but phase transitions of the second kind need not necessarily involve a change in symmetry of the configuration of atoms in the lattice. A transition of the second kind can also bring about a transformation between two phases differing in some other property of symmetry, as for example at the Curie points of ferromagnetic or antiferromagnetic substances. In this case there is a change in symmetry of the arrangement of the elementary magnetic moments in the body, or more precisely a disappearance of the currents j in it; see the first footnote to § 128. Other phase transitions of the second kind are the transition of a metal to the superconducting state (in the absence of a magnetic field) and that of liquid helium to the superfluid state. In both these cases the state of the body changes continuously, but it acquires a qualitatively new property at the transition point.
Since the states of the two phases are the same at a transition point of the second kind, it is clear that the symmetry of the body at the transition point itself must contain all the symmetry elements of both phases. It will be shown below that the symmetry at the transition point itself is the same as the symmetry everywhere on one side of that point, i.e. the symmetry of one of the phases. Thus the change in symmetry of the body in a phase transition of the second kind has the following very important general property: the symmetry of one phase is higher than that of the other.† It should be emphasised that in a phase transition of the first kind the change in symmetry of the body is subject to no restriction, and the symmetries of the two phases may be unrelated.
In the great majority of the known instances of phase transitions of the second kind, the more symmetrical phase corresponds to higher temperatures and the less symmetrical one to lower temperatures. In particular, a transition of the second kind from an ordered to a disordered state always occurs with increasing temperature. This is not a law of thermodynamics, however, and exceptions are therefore possible.‡
For brevity we shall arbitrarily call the more symmetrical phase simply the symmetrical one, and the less symmetrical phase the unsymmetrical one.
To describe quantitatively the change in the structure of the body when it passes through the phase transition point, we can define a quantity η, called the order parameter, in such a way that it takes non-zero (positive or negative) values in the unsymmetrical phase and is zero in the symmetrical phase. For instance, in transitions where the atoms are displaced from their positions in the symmetrical phase, η may be taken as the amount of this displacement For transitions with a change in the ordering of the crystal (e.g. in the CuZn alloy mentioned above), the parameter η may be defined as
where wCu and wZn are the probabilities of finding a copper atom and a zinc atom respectively at any given lattice site. For magnetic transitions, η may be taken as the macroscopic magnetic moment per unit volume of a ferromagnet or the magnetic moment of the sub-lattice for an antiferromagnet.
It must again be emphasised that the symmetry of the body is changed (namely, increased) only when η becomes exactly zero; any non-zero value of the order parameter, however small, brings about a lowering of the symmetry. A passage through a phase transition point of the second kind has a continuous change of η to zero.
The absence of any discontinuous change of state at a phase transition point of the second kind has the result that the thermodynamic functions of the state of the body (its entropy, energy, volume, etc.) vary continuously as the transition point is passed. Hence a phase transition of the second kind, unlike one of the first kind, is not accompanied by evolution or absorption of heat. We shall see, however, that the derivatives of these thermodynamic quantities (i.e. the specific heat of the body, the thermal expansion coefficient, the compressibility, etc.) are discontinuous at a transition point of the second kind.
We must remember that mathematically a phase transition point of the second kind is a singularity of the thermodynamic quantities, and in particular of the thermodynamic potential Φ; the nature of this singularity is discussed in §§ 148 and 149. In order to see this, let us first recall that a phase transition point of the first kind is not a singularity; it is a point at which the thermodynamic potentials Φ1(P, T) and Φ2(P, T) of the two phases are equal, and each of the functions Φ1 and Φ2 on either side of the transition point corresponds to an equilibrium (though possibly metastable) state of the body. In a phase transition of the second kind, however, the thermodynamic potential of each phase, if formally regarded on the far side of the transition point, corresponds to no equilibrium state, i.e. to no minimum of Φ; we shall see in § 143 that the thermodynamic potential of the symmetrical phase would indeed correspond to a maximum of Φ beyond the transition point.
This last result implies that superheating and supercooling effects are impossible in phase transitions of the second kind (whereas they can occur in ordinary phase transitions). In this case neither phase can exist beyond the transition point (here we ignore, of course, the time needed to establish the equilibrium distribution of atoms, which in solid crystals may be considerable).
PROBLEM
Let c be the concentration of atoms of one component of a binary solid solution, and c0 the concentration of these atoms’ “own” sites. If c ≠ c0 the crystal cannot be completely ordered. Assuming the difference c–c0 small and the crystal almost completely ordered, determine the concentration λ of atoms at “other” sites, expressing it in terms of the value λ0 which it would have at c = c0 for given P and T(C. Wagner and W. Schottky, 1930).
SOLUTION.
Considering throughout only the atoms of one component, we use the concentration λ of atoms at other sites and the concentration λ′ of their own sites not occupied by these atoms; concentrations are defined with respect to the total number of all atoms in the crystal. Clearly
We shall regard the crystal as a “solution” of atoms at other sites and of own sites not occupied by atoms, the “solvent” being represented by atoms at their “own” sites. The transition of atoms from “other” to their “own” sites can then be regarded as a “chemical reaction” between the “solutes” (with small concentrations λ and λ′) to form the “solvent” (with concentration ≅ 1). Applying to this “reaction” the law of mass action, we obtain λλ′ = K, where K depends only on P and T. For c = c0 we must have λ = λ′ ≡ λ0; hence  , and so
, and so
§ 143 The discontinuity of specific heat
The quantitative theory of phase transitions of the second kind is based on a consideration of the thermodynamic quantities of the body for given deviations from the symmetrical state (i. e. for given values of the order parameter η); we can represent the thermodynamic potential of the body, for example, as a function of P, T and η. Here it must of course be remembered that in the function Φ(P, T, η) the variable η is in one sense not on the same footing as the variables P and T; whereas the pressure and temperature can be specified arbitrarily, the value of η which actually occurs must itself be determined from the condition of thermal equilibrium, i.e. the condition that Φ is a minimum (for given P and T).
The continuity of the change of state in a phase transition of the second kind is expressed mathematically by the fact that the quantity η takes arbitrarily small values near the transition point. Considering the neighbourhood of this point, we expand Φ(P, T, η) in powers of η:
where the coefficients ∝, A, B, C, … are functions of P and T.
It must emphasised, however, that writing Φ as the regular expansion (143.1) does not take account of the fact already mentioned that the transition point is a singularity of the thermodynamic potential; the same is true of the later expansion of the coefficients in (143.1) in powers of the temperature. This section and §§ 144–146 are concerned with a theory† based on the validity of such expansions; the conditions for it to be applicable will be considered in § 146.
It can be shown (see § 144) that, if the states with η = 0 and η ≠ 0 are of different symmetry (as we assume), the first-order term in the expansion (143.1) is identically zero: ∝ ≡ 0. The coefficient A(P, T) in the second-order term is easily seen to vanish at the transition point, since in the symmetrical phase the value η = 0 must correspond to a minimum of Φ, and for this to be so it is evident that A > 0 is necessary, while on the other side of the transition point, in the unsymmetrical phase, non-zero values of η must correspond to the stable state (i. e. to the minimum of Φ), and this is possible only if A < 0; FIG. 62 shows the form of the function Φ(η) for A < 0 and A > 0. Since A is positive on one side of the transition point and negative on the other, it must vanish at the transition point itself.

FIG. 62
But if the transition point itself is a stable state, i. e. if Φ as a function of η is a minimum at η = 0, it is necessary that the third-order term should be zero and the fourth-order term positive there:
where the suffix c refers to the transition point.
The coefficient B, being positive at the transition point, is of course also positive in the neighbourhood of that point.
Two cases can occur. In one, the third-order term is identically zero owing to the symmetry of the body: C(P, T) ≡ 0. Then there remains at the transition point only the one condition A(P, T) = 0, which determines P as a function of T or vice versa. Thus in the PT-plane there is a line of phase transition points of the second kind.†
If, however, C is not identically zero, the transition points are determined by the two equations A(P, T) = 0, C(P, T) = 0. In this case, therefore, the continuous phase transitions can occur only at isolated points.†
The most interesting case is, of course, that where there is a line of continuous-transition points. In what follows we shall take the discussion of phase transitions of the second kind to refer only to this case, which will now be considered. It includes, in particular, transitions due to the appearance or disappearance of a magnetic structure. This is because of the symmetry under time reversal. The thermodynamic potential of the body cannot be altered by this transformation, whereas the magnetic moment (which here acts as the order parameter) changes sign. It is therefore clear that in such cases the expansion of Φ contains no odd-order terms.
We shall therefore suppose that C ≡ 0 and the expansion of the thermodynamic potential has the form
Here B > 0, while the coefficient A > 0 in the symmetrical phase and A < 0 in the unsymmetrical phase; the transition points are determined by the equation A(P, T) = 0.
In the theory given here, it is assumed that the function A(P, T) has no singularity at the transition point, so that it can be expanded near this point in integral powers of the “distance” from the transition:
where Tc = Tc(P) is the transition temperature. The coefficient B(P, T) may be replaced by B(P, Tc). The expansion of the thermodynamic potential therefore becomes
with B(P) > 0.
The dependence of η on the temperature near the transition point, in the unsymmetrical phase, is determined from the condition for Φ to be a minimum as a function of η. Equating the derivative ∂Φ/∂η to zero, we obtain η(A + 2Bη2) = 0, and hence
the solution η = 0 with A < 0 corresponds to a maximum of Φ, not a minimum. It should be noted that the configuration of the two phases on the temperature scale depends on the sign of a: for a > 0 and a < 0, the unsymmetrical phase corresponds to the temperatures T < Tc and T > Tc respectively. We shall assume below the particular case where the symmetrical phase is at T > Tc, as happens in the great majority of cases, and accordingly that a > 0.
Neglecting higher powers of η, we find for the entropy
the term containing the temperature derivative of η is zero, because ∂Φ/∂η = 0. In the symmetrical phase, η = 0 and S = S0; in the unsymmetrical phase,
At the transition point itself, this expression becomes S0, and the entropy is therefore continuous, as it should be.
Finally, let us determine the specific heats Cp = T(∂S/∂T)P of the two phases at the transition point. For the unsymmetrical phase we have, differentiating (143.7),
For the symmetrical phase S = S0, and therefore Cp = Cp0. Thus the specific heat is discontinuous at a phase transition point of the second kind. Since B > 0, Cp > Cp0 at the transition point, i.e. the specific heat increases in going from the symmetrical to the unsymmetrical phase, whatever their respective positions on the temperature scale.
Other quantities besides Cp are discontinuous: Cv, the thermal expansion coefficient, the compressibility, etc. There is no difficulty in deriving relations between the discontinuities of all these quantities. First of all we note that the volume and the entropy are continuous at the transition point, i.e. their discontinuities ΔV and ΔS are zero:
We differentiate these equations with respect to temperature along the curve of transition points, i.e. assuming the pressure to be the function of temperature given by this curve. The result is
since (∂S/∂P)T = —(∂V/∂T)P. These two equations relate the discontinuities of the specific heat Cp, the thermal expansion coefficient and the compressibility at a phase transition point of the second kind (W. H. Keesom and P. Ehrenfest, 1933).
Differentiating along the curve of transition points the equations ΔS = 0 and ΔP = 0 (the pressure is, of course, unchanged in the transition), but with temperature and volume as independent variables, we find
It may be noted that
so that the discontinuities of the specific heat and the compressibility have the same sign. From the previous statement about the discontinuity of the specific heat, it follows that the compressibility decreases discontinuously on going from the unsymmetrical to the symmetrical phase.
To conclude this section, let us return to the first part and consider the meaning of the function Φ(P, T, η).
The formal introduction of this function for any values of η does not, in general, require the possible existence of actual macroscopic states (partial equilibria) corresponding to such values. We must emphasise, however, that such states do in fact exist near a phase transition point of the second kind: as the transition point is approached, the minimum of Φ as a function of η becomes steadily flatter. This means that the “restoring force” that tends to bring the body to the state having the equilibrium value of η becomes steadily weaker, so that the relaxation time for the establishment of equilibrium with respect to the order parameter increases without limit (and certainly becomes much longer than the time for equalisation of pressure throughout the body).
PROBLEM
Find the relation between the discontinuities of specific heat and heat of solution in a transition of the second kind in a solution (I. M. Lifshitz, 1950).
SOLUTION.
The heat of solution per molecule of solute is given by q = ∂W/∂n—w′0, where W is the heat function of the solution and w′0 the heat function per particle of the pure solute. Since w′0 is not affected by the phase transition in solution, we have for the discontinuity of q
where we have used the fact that the chemical potential μ′ = ∂Φ/∂n is continuous at the transition. On the other hand, differentiation of the equation Δ(∂Φ/∂T) = 0 (continuity of entropy) along the curve of the transition temperature as a function of the concentration c at constant pressure gives
Hence we have the required relation
We may note that in the derivation of this relation no assumption has been made concerning the concentration of the solution.
§ 144 Effect of an external field on a phase transition
Let us now consider how the properties of a phase transition change when the body is subjected to an external field whose action depends on the value of the parameter η. Without specifying the physical nature of this field, we may formulate in general terms the assumptions made about it. These amount to asserting that the application of the field is described by the appearance in the Hamiltonian of the body of a perturbing operator having the form
which is linear in the field “strength” h and in the operator  of the quantity μ V is the volume of the body.† If the thermodynamic potential is defined as a function of P, T and h, the mean (equilibrium) value of η is given by
of the quantity μ V is the volume of the body.† If the thermodynamic potential is defined as a function of P, T and h, the mean (equilibrium) value of η is given by
according to the theorem of differentiation with respect to a parameter; cf. (11.4) and (15.11).
In order to ensure that this relation is satisfied in the Landau theory, we must add to the expansion (143.5) a term —ηhV:
with the notation t = T—Tc(P).‡
We may note first of all that any field, however weak, has the result that the parameter η becomes different from zero at every temperature. Thus the field reduces the symmetry of the more symmetrical phase, and so the difference between the two phases disappears. Accordingly, the discrete phase transition point also disappears; the transition is “smoothed out”. In particular, instead of the sharp discontinuity of the specific heat, there is an anomaly spread over a range of temperatures. The order of magnitude of this range can be estimated from the condition ηhV ˜ atη2; taking η from (143.6), we then find
For a quantitative investigation of the transition, we write the equilibrium condition (∂Φ/∂η)T,h = 0:†
The dependence of η on the field h is different for temperatures above and below Tc. It will be recalled that we agreed to take a > 0, so that the temperatures t > 0 (T > Tc) correspond to the symmetrical phase (η = 0 for h = 0)
For t > 0, the left-hand side of equation (144.4) increases monotonically with η (Fig. 63a). The equation therefore has for any given value of h just one (real) root, which vanishes when h = 0. The function η(h) is single-valued, and the sign of η is the same as that of h (Fig. 64a).

FIG. 63

FIG. 64
If t < 0, however, the left-hand side of (144.4) is not a monotonic function of η (Fig. 63b), and so the equation has three different real roots over a certain range of values of h, and η(h) is no longer single-valued (Fig. 64b). This range evidently has limits given by the condition
and is — ht, < h < ht, where
It is easy to see, however, that the whole section of the curve BB′ on which (∂η/∂h)T < 0 corresponds to thermodynamically unstable states: differentiating equation (144.4) with respect to h, we find
hence we see that (∂2Φ/∂η2)T,h < 0 when (∂η/∂h)T < 0, i.e. Φ has a maximum here, not a minimum.
In the sections AB and A′B′ the thermodynamic potential is a minimum, but its value is greater than for the minima corresponding to the sections A′D′ and AD respectively, as is easily seen by direct calculation, although it is also obvious a priori: since the field h appears in Φ as the term –ηhV, it is certainly more favourable thermodynamically for the sign of η to be the same as that of h. Thus the sections AB and A′B′ correspond to metastable states of the body, and the true equilibrium form of the function η(h) is given by the continuous curve DAA′D′ in FIG. 64b, all points of which correspond to thermodynamically stable states. If at a given temperature t < 0 the field is varied, a phase transition of the first kind occurs when it passes through h = 0: at this point phases with values of η = ±(a|t|/2B)1/2 opposite in sign are in equilibrium together.
The susceptibility is determined as the derivative
Differentiation of (144.4) gives
and substitution (as h → 0) of η2 = 0 for t > 0 and η2 = —at/2B for t < 0 leads to the result
The infinite value of χ as t → 0 is a natural consequence of the fact (already mentioned at the end of § 143) that the minimum of Φ(η) becomes steadily flatter as the transition point is approached. Because of this, even a slight perturbation has a great effect on the equilibrium value of η.
gives the value of the field at which the field-induced parameter ηind ˜ χh becomes of the same order of magnitude as the characteristic value of the spontaneous (zero-field) ηsp ˜ (a|t|/B)1/2. Fields h « h1 are “weak” in the sense that they do not affect the thermodynamic quantities of the body in the first approximation. Fields h » h1 are “strong” fields for which the thermodynamic quantities have values determined by the field in the first approximation; evidently, when t = 0, any field is strong in this sense.
In strong fields, the order parameter is
It is also easily verified that in this limit the specific heat Cp is independent of the field.
§ 145 Change in symmetry in a phase transition of the second kind
In the theory given in the preceding sections we have considered a phase transition of the second kind with some definite change in symmetry of the body, assuming a priori that such a transition is possible. Such a theory, however, does not say whether a given change of symmetry can in fact occur by a transition of the second kind. The theory developed in the present section is designed to answer this question; it starts from a different statement of the problem, whereby a certain symmetry of the body at the transition point itself is specified, and we ask what symmetry is possible on either side of this point.
For definiteness, we shall speak of phase transitions involving a change in structure of the crystal lattice, i.e. a change in the symmetry of the configuration of atoms in it. Let ρ(x, y, z) be the density function (defined in § 128), which gives the probability distribution of various positions of the atoms in the crystal. The symmetry of the crystal lattice is the set or group of all transformations of the coordinates under which the function ρ(x, y, z) is invariant. Here we mean, of course, the complete symmetry of the lattice, including rotations, reflections and also the infinite (discrete) set of all possible parallel displacements (translations); that is, we are concerned with one of the 230 space groups.
Let G0 be the symmetry group of the crystal at the transition point itself. As we know from group theory, an arbitrary function ρ(x, y, z) can be represented as a linear combination of several functions ϕ1, ϕ2, … having the property of being transformed into combinations of one another by all the transformations in the group concerned. In general the number of these functions is equal to the number of elements in the group, but when the function ρ itself has a certain symmetry the functions ϕi may be fewer in number.
Bearing this in mind, we write the density function ρ(x, y, z) of the crystal as the sum
where the functions ϕi are transformed into combinations of one another by all transformations in the group G0. The matrices of these transformations form a representation of the group G0. The choice of the functions ϕi is not unique; they can obviously be replaced by any linear combinations of themselves. The functions ϕi can always be so chosen as to form a number of independent sets containing the minimum number of functions, the functions in each set being transformed only into combinations of one another by all transformations in the group G0. The matrices of the transformations of the functions in each of these sets form irreducible representations of the group G0, and the functions themselves are the basis of these representations. Thus we can write
n being the number of the irreducible representation and i the number of the function in its basis. In what follows we shall assume the functions  to be normalised in some definite manner.
to be normalised in some definite manner.
The functions  always include one which is invariant under all the transformations in the group G0 and gives what is called the unit representation of the group. Thus this function (which we denote by ρ0) has the symmetry of G0. Denoting the remaining part of
always include one which is invariant under all the transformations in the group G0 and gives what is called the unit representation of the group. Thus this function (which we denote by ρ0) has the symmetry of G0. Denoting the remaining part of  by δ
by δ , we can write
, we can write
where now the unit representation is excluded from the summation (as indicated by the prime to the summation sign). The function δρ has a lower symmetry than that of G0, since δρ may also remain invariant under some transformations in this group but certainly does not do so under all. We may note that the symmetry G of the function ρ (which clearly is the symmetry of δρ) has, strictly speaking, been assumed from the start to be lower than G0, since otherwise the sum (145.1) would include only one term, the function ρ itself, which gives the unit representation.†
Since the physical quantity δρ must be real and must remain real under all transformations, we must assume physically irreducible representations whose base functions can be taken as real (§ 135); accordingly the functions  are taken to be real.
are taken to be real.
The thermodynamic potential Φ( ) of a crystal whose density function
) of a crystal whose density function  is given by (145.2) is a function of temperature, pressure and the coefficients
is given by (145.2) is a function of temperature, pressure and the coefficients  (and depends, of course, on the specific form of the functions
(and depends, of course, on the specific form of the functions  themselves). The actual values of the
themselves). The actual values of the  as functions of P and T are determined thermodynamically from the conditions of equilibrium, i.e. the conditions for Φ to be a minimum. This determines also the symmetry G of the crystal, since it is clear that the symmetry of the function (145.2), with functions
as functions of P and T are determined thermodynamically from the conditions of equilibrium, i.e. the conditions for Φ to be a minimum. This determines also the symmetry G of the crystal, since it is clear that the symmetry of the function (145.2), with functions 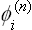 whose laws of transformation are known, is determined by the values of the coefficients in the linear combination of the
whose laws of transformation are known, is determined by the values of the coefficients in the linear combination of the  .
.
If the crystal is to have the symmetry G0 at the transition point itself, it is necessary that all the  should be zero there, i.e. δρ = 0, ρ = ρ0. Since the change in state of the crystal in a phase transition of the second kind is continuous, δρ must tend continuously to zero at the transition point, not discontinuously, i.e. the coefficients
should be zero there, i.e. δρ = 0, ρ = ρ0. Since the change in state of the crystal in a phase transition of the second kind is continuous, δρ must tend continuously to zero at the transition point, not discontinuously, i.e. the coefficients  must tend to zero through arbitrarily small values near the transition point. Accordingly, we can expand the potential Φ(P, T,
must tend to zero through arbitrarily small values near the transition point. Accordingly, we can expand the potential Φ(P, T,  ) in powers of the
) in powers of the  near the transition point.
near the transition point.
First of all let us note that, since the functions  (belonging to the basis of each irreducible representation) are transformed into combinations of one another by the transformations in the group G0, these transformations can be regarded as transforming (in the same manner) the coefficients
(belonging to the basis of each irreducible representation) are transformed into combinations of one another by the transformations in the group G0, these transformations can be regarded as transforming (in the same manner) the coefficients  instead of the functions
instead of the functions  . Next, since the thermodynamic potential of the body must obviously be independent of the choice of coordinates, it must be invariant under any transformation of the coordinate system. If such a transformation converts ρ = ρ0 + δρ into ρ′ = ρ′0 + δρ′, then
. Next, since the thermodynamic potential of the body must obviously be independent of the choice of coordinates, it must be invariant under any transformation of the coordinate system. If such a transformation converts ρ = ρ0 + δρ into ρ′ = ρ′0 + δρ′, then
Now let the transformation belong to the group G0, which leaves ρ0 invariant. Then
Thus, if the potential Φ is regarded as a functional of δρ only, with a given function ρ0, it will be invariant under transformations of the group G0, and only them. Thus the expansion of Φ in powers of the  can contain in each term only an invariant combination of the
can contain in each term only an invariant combination of the  that is of the appropriate power.
that is of the appropriate power.
No linear invariant can be formed from quantities which are transformed according to a (non-unit) irreducible representation of a group, for otherwise that representation would contain the unit representation, i.e. would be reducible. Only one second-order invariant exists for each representation: a positive-definite quadratic form in the  , which can always be reduced to a sum of squares.
, which can always be reduced to a sum of squares.
Thus the leading terms in the expansion of Φ are of the form
where the A(n) are functions of P and T.
At the transition point itself, the crystal must have the symmetry G0, i.e. the equilibrium values of the  must be zero. It is evident that Φ can have a minimum when every
must be zero. It is evident that Φ can have a minimum when every  only if all the A(n) are nonnegative.
only if all the A(n) are nonnegative.
If all the A(n) were positive at the transition point, they would also be positive near that point, so that the  would remain zero and there would be no change of symmetry. For some
would remain zero and there would be no change of symmetry. For some  to be non-zero, one of the coefficients A(n) must change sign, and this coefficient must therefore vanish at the transition point.† (Two coefficients A(n) can vanish simultaneously only at an isolated point in the PT-plane, which is the intersection of more than one line of transitions of the second kind.)
to be non-zero, one of the coefficients A(n) must change sign, and this coefficient must therefore vanish at the transition point.† (Two coefficients A(n) can vanish simultaneously only at an isolated point in the PT-plane, which is the intersection of more than one line of transitions of the second kind.)
Thus on one side of the transition point all the A(n) > 0, and on the other side one of the coefficients A(n) is negative. Accordingly, all the  are always zero on one side of the transition point, and on the other side non-zero
are always zero on one side of the transition point, and on the other side non-zero  appear. We conclude, therefore, that on one side of the transition point the crystal has the higher symmetry G0, which is retained at the transition point itself, while on the other side of the transition point the symmetry is lower, and so the group G is a sub-group of the group G0.
appear. We conclude, therefore, that on one side of the transition point the crystal has the higher symmetry G0, which is retained at the transition point itself, while on the other side of the transition point the symmetry is lower, and so the group G is a sub-group of the group G0.
The change in sign of one of the A(n) causes the appearance of non-zero  belonging to the nth representation. Thus the crystal with symmetry G0 becomes one with density ρ = ρ0 + δρ, where
belonging to the nth representation. Thus the crystal with symmetry G0 becomes one with density ρ = ρ0 + δρ, where
is a linear combination of the base functions of any one of the irreducible representations of the group G0 (other than the unit representation). Accordingly we shall henceforward omit the index n which gives the number of the representation, meaning always the one which corresponds to the transition considered.
(so that  ) and write the expansion of Φ as
) and write the expansion of Φ as
where  are invariants of the third, fourth, etc., orders formed from the quantities γi; in the sums over a there are as many terms as there are independent invariants of the appropriate order which can be formed from the γi. In this expansion of the thermodynamic potential, the coefficient A must vanish at the transition point. In order that the transition point itself should be a stable state (i.e. in order that Φ should have a minimum at that point when ηi = 0), the third-order terms must vanish and the fourth-order terms must be positive-definite. As has been mentioned in § 143, a line of phase transitions of the second kind (in the PT-plane) can exist only if the third-order terms in the expansion of Φ vanish identically. This condition may now be formulated as requiring that it should be impossible to construct from the ηi third-order invariants which are transformed according to the corresponding irreducible representation of the group G0.†
are invariants of the third, fourth, etc., orders formed from the quantities γi; in the sums over a there are as many terms as there are independent invariants of the appropriate order which can be formed from the γi. In this expansion of the thermodynamic potential, the coefficient A must vanish at the transition point. In order that the transition point itself should be a stable state (i.e. in order that Φ should have a minimum at that point when ηi = 0), the third-order terms must vanish and the fourth-order terms must be positive-definite. As has been mentioned in § 143, a line of phase transitions of the second kind (in the PT-plane) can exist only if the third-order terms in the expansion of Φ vanish identically. This condition may now be formulated as requiring that it should be impossible to construct from the ηi third-order invariants which are transformed according to the corresponding irreducible representation of the group G0.†
Assuming this condition to be satisfied, we write the expansion as far as the fourth-order terms in the form
Since the second-order term does not involve the γi, the latter are determined simply from the condition for a minimum of the fourth-order terms, i.e. of the coefficient of η4 in (145.7).† Denoting the minimum value of this coefficient simply by B(P, T) (which must be positive, as shown above), we return to the expansion of Φ in the form (143.3), η being determined from the condition that Φ is a minimum regarded as a function of η alone, as in § 143. The values of the γi thus found determine the symmetry of the function
i.e. the symmetry G of the crystal which is formed in the transition of the second kind from a crystal of symmetry G0.‡
In this formalism, the set of quantities ηi acts as an order parameter describing the difference between the unsymmetrical and symmetrical phases. We see that in general this parameter has several components; the ratios γi = ηi/η determine the symmetry of the unsymmetrical phase, and the common factor η gives a quantitative measure of the deviation from the specified symmetry.
The conditions derived above, however, are not yet sufficient to ensure the possibility of a phase transition of the second kind. A further essential condition is obtained if we consider a fact (hitherto deliberately ignored) relating to the classification properties of representations of space groups.§ We have seen in § 134 that these representations can be classified not only by a discrete parameter (such as the number of the small representation) but also by the parameter k, which takes a continuous series of values. The coefficients A(n) in the expansion (145.3) must therefore depend not only on the discrete number n but also on the continuous variable k.
Let a phase transition correspond to the vanishing (as a function of P and T) of the coefficient A(n)(k) with a given number n and a given k = k0. In order that the transition should actually occur, it is necessary that A(n) as a function of k should have a minimum for k = k0 (and therefore for all vectors of the star of k0), i.e. the expansion of A(n) (k) in powers of k—k0 about k0 should contain no linear terms. Otherwise, some coefficients A(n)(k) necessarily vanish before A(n)(k0) and a transition of the type in question cannot occur. A convenient formulation of this condition can be obtained on the basis of the following arguments.
The value of k0 determines the translational symmetry of the functions ϕi, and therefore that of the function δρ (145.8), i.e. it determines the periodicity of the lattice of the new phase. This structure must be stable in comparison with those which correspond to values of k close to k0. But a structure with k = k0 + x (where x is small) differs from that with k = k0 by a spatial “modulation” in the periodicity of the latter, that is, by the appearance of non-uniformity over distances (˜ 1/x) which are large compared with the periods (cell dimensions) of the lattice. Such non-uniformity can be macroscopically described by regarding the parameters ηi as slowly varying functions of the coordinates (whereas the functions ϕi oscillate over interatomic distances). Thus we obtain the requirement that the state of the crystal should be stable with respect to loss of macroscopic homogeneity.†
When the quantities ηi, are not constant in space, the thermodynamic potential per unit volume of the crystal will depend not only on the ηi but also on their derivatives with respect to the coordinates (in the first approximation, on the first derivatives). Accordingly Φ (for unit volume) must be expanded in powers of the ηi and of their gradients  ηi near the transition point. If the thermodynamic potential (of the whole crystal) is to be a minimum for constant ηi, it is necessary that the first-order terms in the gradients in this expansion should vanish identically. (The terms quadratic in the derivatives must be positive-definite, but this imposes no restriction on the ηi, since such a quadratic form exists for ηi which are transformed by any of the irreducible representations.)
ηi near the transition point. If the thermodynamic potential (of the whole crystal) is to be a minimum for constant ηi, it is necessary that the first-order terms in the gradients in this expansion should vanish identically. (The terms quadratic in the derivatives must be positive-definite, but this imposes no restriction on the ηi, since such a quadratic form exists for ηi which are transformed by any of the irreducible representations.)
Among the terms linear in the derivatives, the only ones that can be of interest are those simply proportional to ∂ηi/∂x, …, and those containing the products ηi ∂ ηk/∂x, …. The higher-order terms are clearly of no importance. The thermodynamic potential of the whole crystal, i.e. the integral ∫ Φ dV over the whole volume, is to be a minimum. The integration of all the total derivatives in Φ gives a constant which does not affect the determination of the minimum of the integral. We can therefore omit all terms in Φ which are simply proportional to derivatives of the ηi. Among the terms containing products ηi∂ ηk/∂x, … we can omit all symmetrical combinations  , leaving the antisymmetrical parts
, leaving the antisymmetrical parts
The expansion of Φ can contain only invariant linear combinations of the quantities (145.9). Hence the condition for a phase transition to be possible is that such invariants do not appear.
The components of the gradients  ηi are transformed as the products of the components of a vector and the quantities ηi. The differences (145.9) are therefore transformed as the products of the components of a vector and the antisymmetrised products of the quantities ηi. Consequently the requirement that no linear scalar can be formed from the quantities (145.9) is equivalent to the requirement that no combinations which transform as the components of a vector can be formed from the antisymmetrised products
ηi are transformed as the products of the components of a vector and the quantities ηi. The differences (145.9) are therefore transformed as the products of the components of a vector and the antisymmetrised products of the quantities ηi. Consequently the requirement that no linear scalar can be formed from the quantities (145.9) is equivalent to the requirement that no combinations which transform as the components of a vector can be formed from the antisymmetrised products
here the ϕi and ϕ′i are the same base functions of the relevant irreducible representation, which we regard as taken at two different points x, y, z and x′, y′, z′ in order that the difference shall not be identically zero.† Labelling the base functions by the two suffixes k∝ (as in § 134), we write the difference (145.10) in the form
where k, k′, … are vectors of the same star.
Let the vector k occupy the most general position and have no proper symmetry. The star of k contains n vectors according to the number of rotational elements in the group (or 2n if the space group itself does not include inversion), each k being accompanied by the different vector —k. The corresponding irreducible representation is given by the same number of functions ϕk (one for each k, and so we omit the suffix ∝). The quantities
are invariant under translations. Under the rotational elements, these n (or 2n) quantities are transformed into combinations of one another, giving a representation of the corresponding point group (crystal class) with dimension equal to the order of the group. But this representation (called a regular representation) contains all the irreducible representations of the group, including those by which the components of a vector are transformed.
Similar considerations show that it is possible to form a vector from the quantities χkα, −kβ in cases where the group of the vector k contains one axis and planes of symmetry passing through that axis.
This discussion becomes inapplicable, however, if the group of the vector k contains axes which intersect one another or intersect planes of symmetry, or contains inversion; such groups will be said to have a central point. In such cases the question of constructing a vector from the quantities (145.11) requires separate treatment in each particular case. In particular, such a vector certainly can not be constructed if the group of k contains inversion, so that k and −k are equivalent, and only one function ϕk corresponds to each k in the star; in this case there are no χkk′ invariant under translations (as the components of a vector must necessarily be).
Thus the requirement formulated above greatly restricts the possible changes of symmetry in a phase transition of the second kind. Of the infinity of different irreducible representations of the group G0, we need consider only a comparatively small number for which the group of the vector k has a central point.
A proper symmetry of this kind can, of course, occur only for vectors k which occupy certain exceptional positions in the reciprocal lattice, their components being equal to certain simple fractions  of the basic vectors of that lattice. This means that the change in the translational symmetry of the crystal (i.e. in its Bravais lattice) in a phase transition of the second kind must consist in an increase by a small factor in some of the basic lattice vectors. Investigation shows that in the majority of cases the only possible change in the Bravais lattice is a doubling of the lattice vectors. In addition, in body-centred orthorhombic, tetragonal and cubic and face-centred cubic lattices some lattice vectors can be quadrupled, and in a hexagonal lattice tripled. The volume of the unit cell can be increased by a factor of 2,4 or 8, in a face-centred cubic lattice also by 16 or 32, and in a hexagonal lattice by 3 or 6.
of the basic vectors of that lattice. This means that the change in the translational symmetry of the crystal (i.e. in its Bravais lattice) in a phase transition of the second kind must consist in an increase by a small factor in some of the basic lattice vectors. Investigation shows that in the majority of cases the only possible change in the Bravais lattice is a doubling of the lattice vectors. In addition, in body-centred orthorhombic, tetragonal and cubic and face-centred cubic lattices some lattice vectors can be quadrupled, and in a hexagonal lattice tripled. The volume of the unit cell can be increased by a factor of 2,4 or 8, in a face-centred cubic lattice also by 16 or 32, and in a hexagonal lattice by 3 or 6.
Transitions are, of course, also possible without change of Bravais lattice (corresponding to irreducible representations with k = 0). The change in symmetry then consists in a decrease in the number of rotational elements, i.e. a change in the crystal class.
We may note the following general theorem. A phase transition of the second kind can occur for any change in structure which halves the number of symmetry transformations; such a change may occur either by a doubling of the unit cell for a given crystal class or by a halving of the number of rotations and reflections for a given unit cell. The proof is based on the fact that, if the group G0 has a sub-group G of half the order, then the irreducible representations of G0 always include a one-dimensional representation given by a function which is invariant under all transformations of the sub-group G and changes sign under all the remaining transformations of the group G0. It is clear that in this case there are no odd-order invariants, and no quantities of the type (145.11) can be formed from one function.
The following theorem also appears to be valid. Phase transitions of the second kind cannot occur for changes in structure which reduce to one-third the number of symmetry transformations, owing to the presence of third-order terms in the expansion of Φ.
Finally, to illustrate the practical applications of the general theory given above, let us consider the occurrence of ordering in alloys which, in the disordered state, have a body-centred cubic lattice with atoms at the vertices and centres of cubic cells, as in Fig. 61b (§ 142).† The problem is to determine the possible types of ordering (called superlattices in crystallography) which can appear in such a lattice in a phase transition of the second kind.
For a body-centred cubic lattice, the reciprocal lattice is face-centred cubic, If the edge of the body-centred cubic lattice cell is taken as the unit of length, the edge length of the cubic cell in the reciprocal lattice is 2·2π, and in this lattice the following vectors k have proper symmetry groups with a central point:
These symbols show the components of the vectors k along the edges of the cubic reciprocal lattice cell (x, y, z axes) as fractions of the edge lengths. In order to obtain the vectors k in the units specified above, these numbers must be multiplied by 2·2π = 4π. In (145.13) only non-equivalent vectors are shown, i.e. the vectors of each star.
The subsequent discussion is greatly simplified by the fact that not all small representations need be considered in solving the problem in question. The reason is that we are concerned only with the possible changes of symmetry that can occur by the formation of a superlattice, that is, by an ordered arrangement of atoms at existing lattice sites without relative displacement. In this case the unit cell of the disordered lattice contains only one atom. Hence the appearance of the superlattice can only mean that the lattice points in different cells become non-equivalent. The change δρ in the density distribution function must therefore be invariant under all rotational transformations of the group of k (without simultaneous translation). Thus only the unit small representation is admissible, and accordingly u∝ may be replaced by unity in the base functions (134.3).
Let us now consider in turn the stars listed in (145.13).
(a) The function with k = 0 has complete translational invariance, i.e. in this case the unit cell is unchanged, and since each cell contains only one atom no change of symmetry can occur.
(b) The function  corresponds to this k. The linear combination (of this function and the functions obtained from it by all rotations and reflections) which has the symmetry Oh of the group of k is
corresponds to this k. The linear combination (of this function and the functions obtained from it by all rotations and reflections) which has the symmetry Oh of the group of k is
The symmetry of the phase formed is that of the density function ρ = ρ0 + δρ, δρ = ηϕ.† The function ϕ is invariant under all transformations of the class Oh and under translations along any edge of the cubic cell, but not under a translation through half the space diagonal,  . Hence the ordered phase has a simple cubic Bravais lattice with two non-equivalent points in the unit cell, (000) and
. Hence the ordered phase has a simple cubic Bravais lattice with two non-equivalent points in the unit cell, (000) and  ; these will be occupied by different atoms. The alloys which can be completely ordered in this way have the composition AB (e.g. the alloy CuZn mentioned in § 142).
; these will be occupied by different atoms. The alloys which can be completely ordered in this way have the composition AB (e.g. the alloy CuZn mentioned in § 142).
(c) The functions corresponding to these k which have the symmetry Td are
From these we can form two fourth-order invariants:  and
and  . The expansion of Φ (145.7) therefore has the form
. The expansion of Φ (145.7) therefore has the form
Here two cases must be distinguished. Let B2 < 0; then Φ as a function of γ1 and γ2, with the added condition  , has a minimum for γ1 = 1, γ2 = 0. The function δρ = ηϕ1 has the symmetry of the class Oh with a face-centred Bravais lattice, whose cubic cell has a volume 8 times that of the original cubic lattice cell. The unit cell contains 4 atoms; the cubic cell, 16 atoms. By placing like atoms at equivalent lattice sites we find that this superlattice corresponds to a ternary alloy of composition ABC2 with atoms in the following positions:
, has a minimum for γ1 = 1, γ2 = 0. The function δρ = ηϕ1 has the symmetry of the class Oh with a face-centred Bravais lattice, whose cubic cell has a volume 8 times that of the original cubic lattice cell. The unit cell contains 4 atoms; the cubic cell, 16 atoms. By placing like atoms at equivalent lattice sites we find that this superlattice corresponds to a ternary alloy of composition ABC2 with atoms in the following positions:
here the coordinates of the atoms are given in units of the edge length of the new cubic lattice cell, which is twice that of the original cell (see Fig. 65a); “& cyclic” denotes cyclic interchange. If the B and C atoms are identical we obtain an ordered lattice of composition AB3.

FIG. 65
Now let B2 > 0. Then Φ has a minimum at  , so that
, so that  , which leads to the same result).† This function has the symmetry of the class Oh with the same face-centred Bravais lattice as in the preceding case but only two sets of equivalent points, which can be occupied by atoms of two kinds A and B:
, which leads to the same result).† This function has the symmetry of the class Oh with the same face-centred Bravais lattice as in the preceding case but only two sets of equivalent points, which can be occupied by atoms of two kinds A and B:
(see Fig. 65b).
(d) The following functions with the required symmetry D2h correspond to these vectors k:
From these we can form one third-order invariant and four fourth-order invariants, and so the expansion (145.6) becomes
Because cubic terms are present, a phase transition of the second kind is impossible in this case. To examine whether isolated points of continuous transition can exist and the properties of such points (see § 150) it would be necessary to investigate the behaviour of the function Φ near its minimum; we shall not pause to do so here.
The above example shows what rigid limitations are imposed by the thermodynamic theory on the possibility of phase transitions of the second kind; for example, in this case they can exist only when superlattices of three types are formed.
The following fact may also be pointed out. In case (c), when B2 < 0, the actual change in the density function, δρ = ηϕ1, corresponds to only one of the two parameters γ1, γ2 which appear in the thermodynamic potential (145.16). This illustrates an important feature of the foregoing theory: in considering a particular change in the lattice in a phase transition of the second kind, it may be necessary to take account of other, “virtually possible”, changes.
§ 146 Fluctuations of the order parameter
It has already been mentioned several times that the actual point of a phase transition of the second kind is a singularity of the thermodynamic functions for the body. The physical nature of this singularity consists in an anomalous increase in the fluctuations of the order parameter, which in turn is due to the already described flatness of the thermodynamic potential minimum near the transition point. The form of this increase in the Landau model is easily found. We shall assume that the change of symmetry in the transition is described by only one parameter η.
The minimum work needed to bring the system out of equilibrium for given constant values of the pressure and temperature is equal to the change δΦt in the thermodynamic potential.† The fluctuation probability for constant P and T is therefore
In this section the equilibrium value of η will be denoted by 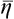 . For a small departure from equilibrium,
. For a small departure from equilibrium,
By means of (144.6) we can express the derivative ∂2Φt/∂η2 in terms of the susceptibility of the substance in a weak field, according to the definition (144.7). Then the fluctuation probability (at temperatures near the transition point Tc) is
Hence the mean square fluctuation is
This expression can also be derived directly from the fluctuation–dissipation theorem. To do so, we need only note that, if the field h is identified with the external interaction f (with frequency Ω = 0) which appears in the formulation of the theorem (§ 124), then the corresponding quantity x is δηV, and the generalised susceptibility ∝(0) is the product χV. Formula (146.2) follows from (124.14).
According to (144.8), the mean square (146.2) increases as 1/t when T → Tc. For a fuller elucidation of the nature and significance of this divergence, let us determine the spatial correlation function of the fluctuations of the order parameter. We shall be concerned with long-wavelength fluctuations in which the fluctuating quantity varies slowly through the body; it is these fluctuations which, as we shall see later, increase anomalously near the transition point.
For an inhomogeneous body (such as it becomes when the inhomogeneous fluctuations are taken into account), the thermodynamic potential would have to be expressed as the integral Φt = ∫ Φ dV of the potential density, a function of the coordinates of a point in the body. However, in the description of the thermodynamic state by the potential Φ, the number N of particles in the body is given, not its volume (which depends on P and T). It is therefore useful to change to a description by another potential which relates to some chosen and specified volume V in the medium, containing a variable number N of particles. This can be Ωt(T, μ), a function of temperature and chemical potential μ (for given V); the variable P is here replaced by μ, which has analogous properties; like P, it is constant throughout a system in equilibrium.
Near the transition point, the η-dependent terms in the expansion of the function Φ(P, T, η) (144.3) constitute a small increment to Φ0(P, T), and after η has been determined by minimisation the remaining terms are all of the same order of magnitude. According to the theorem of small increments, we can therefore immediately write down a similar expansion for the potential Ω(μ, T, η):
with the same coefficients but expressed in terms of a different variable, μ instead of T; the potential Ω is here taken per unit volume, and so the coefficients are ∝ = a/V, b = B/V.†
The expansion (146.3) relates to a homogeneous medium. In an inhomogeneous body, it includes not only different powers of η itself but also derivatives of various orders with respect to the coordinates. For long-wavelength fluctuations, we need take only the terms in the expansion that contain derivatives of the lowest order (and the lowest powers of these). The terms linear in the first-order derivatives, of the form f(η) ∂η/∂xi, give integrals over the surface on integration through the volume, which represent a surface effect unimportant here.‡ The same is true of terms proportional to ∂2η/∂xi∂xk. Thus the first terms to be taken into account in the expansion of Ω in derivatives are those proportional to η∂2η/∂xi∂xk or (∂η/∂xi)(∂η/∂xk). The former reduce to the latter on integration over the volume. We find ultimately that the function Ω written above has to be supplemented by terms of the form
as always, summation over repeated vector suffixes is implied. We shall take only the simplest case (corresponding to cubic symmetry with η = 0), when gik = gδik; this case already shows all the characteristic features of the correlation function. Thus we write the thermodynamic potential density as
It is evident that, for stability of a homogeneous body, g > 0; otherwise, Ωt cannot have a minimum when η = constant.
Considering fluctuations for given μ and T, we must write their probability as
since the minimum work needed in these conditions to bring the system out of equilibrium is Rmin = − δΩt. Specifying the value of η in a chosen volume V does not prevent the exchange of particles (or energy) between this volume and the surrounding “medium”. We can therefore consider the fluctuations of η for constant μ (and T); cf. the beginning of § 115.
Let us take the particular case of fluctuations in the symmetrical phase (in the absence of a field h); then  , so that δη = η. As far as the second-order terms, the change in the potential Ωt is†
, so that δη = η. As far as the second-order terms, the change in the potential Ωt is†
We now proceed as in § 116, expanding the fluctuation δη(r) as a Fourier series in the volume V:
the gradient is
On substitution of these expressions in (146.6), the integration over the volume causes all terms to vanish except those which contain the products δηkδη—k = |δηk|2. The result is
and hence
cf. the derivation of (116.12) from (116.10). We see that as t → 0 it is in fact the long-wavelength fluctuations with k ˜ 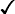 (∝t/g) which increase.† It must be emphasised that the formula (146.8) itself is valid only for sufficiently long wavelengths 1/k, which must always be large compared with interatomic distances.
(∝t/g) which increase.† It must be emphasised that the formula (146.8) itself is valid only for sufficiently long wavelengths 1/k, which must always be large compared with interatomic distances.
The required correlation function will be denoted by
and is calculated as the sum
or, changing to integration in k-space,
Using the Fourier transformation formula given in the footnote to § 117, Problem 3, we find (for r ≠ 0)
where
is called the correlation radius of the fluctuations; it determines the order of magnitude of distances at which the correlation decreases significantly. As the transition point is approached, the correlation radius increases as 1/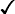 t, and at the transition point itself the correlation function decreases as 1/r.
t, and at the transition point itself the correlation function decreases as 1/r.
When r = 0, the integral (146.10) determines the mean square fluctuation of the parameter η in an infinitesimal volume element; it diverges for large k. This divergence, however, is simply due to the invalidity, in this region, of the expression (146.8) (which relates to long-wavelength fluctuations), and signifies only that  contains a term independent of t.
contains a term independent of t.
It must be emphasised, to avoid misunderstanding, that the previous expression (146.2) determines the fluctuations of the parameter η averaged over a volume V whose linear dimension l » rc; this quantity may be denoted by 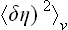 . The mean value of the function δη(r) over the volume V is just the Fourier component δηl = 0; it is therefore natural that the expression (146.8) for k = 0 coincides with (146.2). The latter can also be derived from the correlation function by the obvious formula
. The mean value of the function δη(r) over the volume V is just the Fourier component δηl = 0; it is therefore natural that the expression (146.8) for k = 0 coincides with (146.2). The latter can also be derived from the correlation function by the obvious formula
which is valid for any finite volume V. We may note that at the point t = 0 itself (where G ∝ 1/r) this integral is proportional to 1/l, where l is the linear dimension of the region in which the fluctuations are considered. The mean square  depends on the shape of the region as well as on its volume.
depends on the shape of the region as well as on its volume.
We can now formulate the condition that determines the validity of this theory of fluctuations based on the expansion (146.5). This condition must be that the mean square fluctuation of the parameter η averaged over the correlation volume is small compared with the characteristic value  . This quantity is given by (146.2) when
. This quantity is given by (146.2) when  , and we arrive at the condition
, and we arrive at the condition
or (with χ and rc from (144.8) and (146.12))
(A. P. Levanyuk, 1959; V. L. Ginzburg, 1960).†
The determination of the temperature dependences in the formulae derived above has also required expansions in powers of t = T—Tc (in the coefficients of the expansion with respect to η). The admissibility of such an expansion implies that the condition t « Tc is satisfied; for it to be compatible with (146.15), we must certainly have
The conditions (146.14)–(146.16) ensure that the fluctuations are sufficiently small, and also that the whole Landau theory of phase transitions given in the preceding sections is applicable. We see that a temperature range in which this theory is valid exists only if the inequality (146.16) is satisfied. In such cases, the conclusions of the theory remain valid as regards the selection rules for the possible changes of symmetry in transitions.† As regards the temperature dependence of the thermodynamic quantities, however, there is necessarily a narrow range of temperatures near Tc where the Landau theory is inapplicable. The conclusions of this theory must therefore refer only to states of the two phases outside that temperature range. For example, the expressions derived in § 143 for the discontinuities of the thermodynamic quantities are to be regarded as the differences of their values at the two ends of the range. We shall call the immediate neighbourhood of the point Tc, corresponding to the opposite of the inequality (146.15), the fluctuation range; in it, the fluctuations play the dominant role.
In the above calculations, no account has been taken of the elastic properties that distinguish a solid from a liquid,‡ or the deformation of a body in consequence of ordering (which we shall call striction). Within the Landau theory, these effects do not alter the conclusions reached in the preceding sections. The combined action of the two effects may, however, considerably alter the fluctuations of the order parameter, and therefore the nature of the phase transition. The investigation of this problem demands an extensive use of elasticity theory, and is therefore outside the scope of the present volume. Here, we shall simply state some results.
The striction deformation may be either linear or quadratic in the order parameter, depending on the symmetry of the crystal. These two cases show a different influence of the elastic properties of the body on the phase transition.
For linear striction, let γ denote the order of magnitude of the proportionality coefficients between the components uik of the deformation tensor and the order parameter: uik ˜ γη. The influence of this effect on the fluctuations appears in the neighbourhood of the transition point for which  , where λ is the order of magnitude of the elastic moduli of the body. In many cases, striction is a weak effect, and in this sense γ is a small quantity. Then the temperature range mentioned is narrow and lies within the fluctuation range.
, where λ is the order of magnitude of the elastic moduli of the body. In many cases, striction is a weak effect, and in this sense γ is a small quantity. Then the temperature range mentioned is narrow and lies within the fluctuation range.
The long-wavelength fluctuations  are then suppressed, and the correlation radius does not increase beyond values rc ˜
are then suppressed, and the correlation radius does not increase beyond values rc ˜ 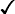 (gλ/γ2). The specific heat therefore has only a finite discontinuity at the transition point, as in the Landau theory.§
(gλ/γ2). The specific heat therefore has only a finite discontinuity at the transition point, as in the Landau theory.§
Quadratic striction leads to different results.† This effect likewise suppresses the fluctuations, but to a smaller extent. Whereas the specific heat would become infinite at the transition point without allowance for striction (see § 148), the quadratic striction leads instead to a small discontinuity of the entropy, i.e. the phase transition is of the first kind and close to the second kind; the specific heat remains finite, although it has anomalously high values.‡
§ 147 The effective Hamiltonian
Before going on to describe the properties of the phase transition outside the range of applicability of the Landau theory (i.e. in the immediate neighbourhood of the transition point) we shall show how the statistical problem of investigating these properties could be formulated.§
According to (35.3), the thermodynamic potential Ω is given by the partition function
where the integration is taken over the whole phase space of a system of N particles. If the integration is taken only over the part of phase space that corresponds to a given distribution of the order parameter η(r), the functional Ω[η(r)] defined by (147.1) may be regarded as the potential corresponding to that distribution. A continuous distribution η(r) may here be conveniently replaced by a discrete set of complex variables ηk = η′k + iη″k, the components in the Fourier expansion (146.7). Then the definition of Ω[η] becomes
where ηk(p, q; N) are the quantities ηk as functions of the point p, q in phase space. It is evident that, with this definition,
In § 146 it has been shown that only fluctuations with small wave vectors k are subject to an anomalous increase near the transition point; these fluctuations therefore govern the nature of the singularity of the thermodynamic functions. At the same time, such quantitative characteristics of the substance as the transition temperature Tc itself are determined mainly by the short-range atomic interactions, which correspond to the short-wavelength components ηk. This physically obvious fact is represented in the integral over states by the correspondence between large values of k and large phase volumes.
Let k0 (the cut-off parameter) be a value of k small compared with the reciprocal of the characteristic atomic dimensions. The long-wavelength part of the distribution η(r) is given by the sum
and the thermodynamic potential  corresponding to this distribution is given by (147.2), where the product over k is to be extended only to values k < k0. Accordingly, the relation between
corresponding to this distribution is given by (147.2), where the product over k is to be extended only to values k < k0. Accordingly, the relation between  and Ω is given by (147.3) with integration only over
and Ω is given by (147.3) with integration only over  with k < k0.†
with k < k0.†
Near the transition point, the functional  can be expanded in powers of the function
can be expanded in powers of the function  ; since this function is a slowly varying one, we need take in the expansion only the terms of lowest order in its derivatives. The expansion must also take into account the existence of the phase transition, since the value of Tc is determined by the short-wavelength components excluded from
; since this function is a slowly varying one, we need take in the expansion only the terms of lowest order in its derivatives. The expansion must also take into account the existence of the phase transition, since the value of Tc is determined by the short-wavelength components excluded from  . This means that the expansion of
. This means that the expansion of  must have the form (146.5) directly:
must have the form (146.5) directly:
Finally, omitting the tilde, we arrive at the following expression for the thermodynamic potential Ω:
where
acts as the effective Hamiltonian of the system undergoing a phase transition.
In the range where the Landau theory is applicable, the fluctuations are small. This means that, in the integral over states (147.5), the important values of η are those lying in a narrow range near the value  that minimises the effective Hamiltonian. Using the saddle-point method (i.e. replacing the exponent by its expansion about the minimum), we ought to recover the thermodynamic potential as in the Landau theory; hence the coefficients in the effective Hamiltonian and in the Landau thermodynamic potential must be exactly the same. The fluctuation corrections, however, cause a certain shift of the transition temperature Tc relative to the value
that minimises the effective Hamiltonian. Using the saddle-point method (i.e. replacing the exponent by its expansion about the minimum), we ought to recover the thermodynamic potential as in the Landau theory; hence the coefficients in the effective Hamiltonian and in the Landau thermodynamic potential must be exactly the same. The fluctuation corrections, however, cause a certain shift of the transition temperature Tc relative to the value  which occurs in (147.6) through the difference
which occurs in (147.6) through the difference  .
.
The integral (147.5) is taken over an infinity of variables ηk (when the effective Hamiltonian has been expressed in terms of these variables by substituting η(r) from (147.4)). If this “continuum integral” could be calculated, we should know the nature of the singularity of Ω(μ, T) near the transition point. The calculation is impossible, however.
In the creation of the singularity, the significant fluctuations are those with wave numbers k ˜ 1/rc. When t → 0, the correlation radius rc → ∞, so that very small values of k become important. It is therefore very probable that the nature of the singularity does not depend on the choice of the cut-off parameter k0. If this singularity is assumed to consist in the presence in the thermodynamic potential of terms containing fractional powers of the temperature t and the field h, the above assertion implies that the indices of these powers (the critical indices) are independent of k0.
Hence it must in turn follow that these indices are independent of the specific values of the coefficients b and g in the effective Hamiltonian, and therefore of μ or P, on which b and g depend. For a change k0 → k0/λ is equivalent to a change in the coordinate scale (r — λr), and such a change therefore cannot affect the critical indices. On the other hand, the transformation r → λr changes the coefficient g in the effective Hamiltonian, but not b; the critical indices must thus be independent of g. Similarly, by making the simultaneous transformations r → λr, and η → λη for the continuum integration variable, we change b but not g, and the critical indices are therefore also independent of b. A change in the coefficient ∝ is unimportant, since it is cancelled by a corresponding change in the scale of t, which cannot affect the exponent.
Thus we should expect that the critical indices are the same for all systems with an effective Hamiltonian of the form (147.6). They may differ, however, if the symmetry of the system is such that (with one order parameter, as before) the term quadratic in the derivatives in the effective Hamiltionian has the more general form (146.4).
Continuing this line of argument, we may expect that in more general cases also, when the change of symmetry in the transition is described by more than one order parameter, the critical indices depend only on the structure of the effective Hamiltonian, not on the specific values of the coefficients in it. Here the “structure” of the Hamiltonian includes the number and form of the fourth-order invariants (and the signs and inequalities relating to their coefficients) and the form of the terms quadratic in the derivatives of the order parameters. The questions then arising, however, have as yet hardly been studied at all.
Lastly, we may add a few remarks on the calculation of the successive terms in the expansion of the partition function (147.5), (147.6) in powers of b. Let h = 0 and t > 0, so that 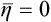 ; when b = 0, the effective Hamiltonian is
; when b = 0, the effective Hamiltonian is
it separates into a sum of terms each depending only on one of the ηk. The integral over states is easily calculated (see Problem). Further terms in the expansion (corresponding to the inclusion of the “interaction” between fluctuations with different k) are products of different ηk averaged over the Gaussian distribution [ ]. For such integrals a theorem is valid whereby the mean value of the product of several ηk is equal to the sum of the products of pairs of mean values of factors chosen in all possible ways from those concerned. Each such mean value is a correlation function of fluctuations (in the k representation), and hence the calculation of the successive terms in the expansion in powers of b amounts to that of various integrals of products of correlation functions.† As the transition point is approached, these integrals diverge, but it is not possible to distinguish among them any set of “most strongly” divergent ones over which a summation could be carried out.†
]. For such integrals a theorem is valid whereby the mean value of the product of several ηk is equal to the sum of the products of pairs of mean values of factors chosen in all possible ways from those concerned. Each such mean value is a correlation function of fluctuations (in the k representation), and hence the calculation of the successive terms in the expansion in powers of b amounts to that of various integrals of products of correlation functions.† As the transition point is approached, these integrals diverge, but it is not possible to distinguish among them any set of “most strongly” divergent ones over which a summation could be carried out.†
In the above formulation of the problem, it is assumed that the nature of the singularity is independent of any higher-order terms in the expansion of the effective Hamiltonian in powers of η. There are good reasons for supposing that this is in fact so, since such terms lead to integrals that diverge less strongly than those resulting from the term ˜ η4.
PROBLEM
Find the first fluctuation correction to the specific heat in the range where the Landau theory is valid (A. P. Levanyuk, 1963).
SOLUTION.
The calculation will be given for the symmetrical phase in the absence of a field. In the first approximation, the effective Hamiltonian is (147.7). A calculation of the integral over states from (147.5) gives
the integration is over half of k-space, since ηk and η—k are not independent. Being the small correction in the potential Ω, this expression also gives the correction to the potential Φ. A twofold differentiation of this expression with respect to t gives the correction to the specific heat:
If this correction is to be small compared with the specific heat discontinuity (143.8), we again obtain the condition (146.15) for the Landau theory to be applicable, in the form
The large numerical factor in the denominator on the right-hand side should be noted.
§ 148 Critical indices
The existing theory of phase transitions of the second kind is based on certain hypotheses that are entirely plausible though not rigorously proved. It rests also, of course, on the confirmation of these hypotheses by experimental results and by numerical calculations for certain simple models.
These results suggest that, as T → Tc, the derivative ∂Cp/∂T always becomes infinite, and so in many cases does the specific heat Cp itself. From this we can already draw various conclusions about the behaviour of certain other thermodynamic quantities. This will be done here on the assumption that the specific heat itself becomes infinite (A. B. Pippard, 1956).
The tending of Cp = T(∂S/∂T)P to infinity means that the entropy of the body can be written as
where P = Pc(T) is the equation of the curve of the points of the phase transition in the PT-plane; the derivative of S with respect to its second argument becomes infinite as P—Pc → 0. Denoting differentiation with respect to that argument by a prime and retaining only the divergent terms, we have
whence
i.e. the thermal expansion coefficient tends to infinity in the same way as Cp.
It is easily seen that this derivation amounts to equating to zero the divergent part of the derivative of S along the curve of transition points. It is therefore natural that (148.1) has the same form as the equation (143.10) obtained by differentiating δS = 0 along the same curve, and differs from it only in the absence of the symbol δ. We can hence write down at once another relation by analogy with (143.9):
i.e. the isothermal compressibility also becomes infinite (but the adiabatic compressibility remains finite, by (16.14)). The specific heat Cv remains finite; from (143.14) we see that it is not even discontinuous at the transition point: since the right-hand side of (143.14) is zero (because (∂V/∂P)T is infinite), δCv = 0.† The same is true of the derivative (∂P/∂T)v; substitution of (148.2) in (16.10) shows that on the transition line
It should be emphasised that the above results essentially depend on the occupation, by the phase transition points of the second kind, of an entire line in the PT-plane, the slope of this line being finite.
Let the temperature dependence of the specific heat in the fluctuation range be written
where again t = T—Tc. We shall see later in this section that there is reason to suppose the values of the exponent ∝ equal on either side of the transition point (and the same is true of the other exponents introduced below). The proportionality factors in (148.4) are, of course, different on the two sides. Since the quantity of heat ∫ Cp dT must always be finite, it follows that ∝ < 1. If only ∂Cp/∂T, and not the specific heat itself, tends to infinity, then — 1 < ∝ < 0; the expression (148.4) in that case determines only the singular part of the specific heat: Cp = Cp0 + Cp1 |t|−α.
The way in which the equilibrium value of the order parameter tends to zero in the unsymmetrical phase may be written as
By definition, the exponent β refers only to the unsymmetrical phase. We shall assume for definiteness here and below that temperatures t < 0 correspond to the unsymmetrical phase.
To describe the properties of the fluctuations themselves of the parameter η, an exponent v is used which defines the temperature dependence of the correlation radius:
and an exponent ζ which gives the decrease of the correlation function with increasing distance at t = 0:
where d is the dimension of space (= 3 for ordinary bodies). The expression (148.7) is written in this form in order to have a definition suitable also for phase transitions of the second kind in two-dimensional systems (d = 2). The law (148.7) is valid also for non-zero |t| « Tc, but only for distances r « rc.
The exponents in (148.4)–(148.7) are called critical indices or critical exponents. It must be emphasised that the degree of accuracy of the subsequent derivation of relations between the critical indices does not allow the distinguishing of logarithmic factors superimposed on power laws. In this sense, for example, a zero exponent may mean either that the quantity tends to a constant limit or that it increases logarithmically.
A further group of indices are used to describe the properties of a body in the fluctuation range when an external field h is present. Here we must distinguish the ranges of fields that are “weak” and “strong” in the sense described at the end of § 144: h « ht or h » ht, where ht is the field value for which the field-induced parameter ηind ˜ χh becomes of the same order as the characteristic value of the spontaneous-order parameter ηsp(t). The region of weak fields has an exponent γ giving the variation of the susceptibility:
The indices defined above may also be assigned to this region: the laws (148.4)–(148.6) derived for zero field relate, of course, also to the limiting case of weak fields.
For the opposite case of strong fields, we define critical indices which give the field dependence of the thermodynamic quantities and the correlation radius:
we take for definiteness the case h > 0.†
The universality of the limiting laws for the behaviour of a substance in the fluctuation range near a phase transition point of the second kind, in the sense discussed in § 147, implies a similar universality of the critical indices. Thus we must expect their values to be the same for all transitions with a change of symmetry described by only one order parameter.
The critical indices are connected by various exact relations. Some of these follow almost immediately from the definitions of the indices, and we shall first derive these.
It has been shown in § 144 that the application of an external field h smooths out the phase transition over a certain temperature range. The magnitude of this range of t can be estimated from the condition ηind(h) ˜ ηsp(t) mentioned above, if this is now taken as a condition on t for given h. According to the definitions (148.5) and (148.8), we have
and equating the two gives
On the other hand, the same smoothing range can be estimated from the requirement that the field part of the thermodynamic potential, — Vηh, is of the same order of magnitude as the thermal part, which is ˜ t2Cp, since Cp = —T∂2Φ/∂T2. Hence we find |t|—2—∝—β ∝ h, and, expressing h in terms of t from (148.12), obtain the equation
(J. W. Essam and M. E. Fisher, 1963).
We next use the obvious fact that, at the edge of the region of smoothing of the transition (i.e. with the condition (148.12)), we can equally well express each thermodynamic quantity in terms of the temperature t or the field h. Hence we find, for example,
and, expressing h in terms of t from (148.12), obtain the equation
(B. Widom, 1964). By a similar method starting from the two limiting forms of the specific heat Cp, we find
The Equation (148.14) and Equation (148.15) relate the indices that determine the temperature dependence of the thermodynamic quantities in weak fields and their dependence on h in strong fields.
An analogous equation is found by the same method for the indices giving the behaviour of the correlation radius:
Lastly, one further relation can be derived by an estimate of the expressions on either side of (146.13). According to (146.2) and the definition (148.8), the mean square fluctuation in a given volume V is
The integral of the correlation function is determined by the region of space  in which this function is considerably different from zero and, according to the definition (148.7), its order of magnitude is
in which this function is considerably different from zero and, according to the definition (148.7), its order of magnitude is  . Hence the magnitude of the integral is (in d-dimensional space)
. Hence the magnitude of the integral is (in d-dimensional space)
A comparison of the two expressions gives
Thus we have five relations between the eight indices, and so they can all be expressed in terms of only three independent ones.
From this we can, in particular, draw the conclusion already mentioned, that the values of the “temperature” indices ∝, γ, v are the same on both sides of the transition point: for, if γ, say, were different for t > 0 and t < 0, it would follow from (148.14) that δ also depends on the sign of t. This index, however, relates to strong fields h, which satisfy only the condition h » h, independent of the sign of t, and it too therefore cannot depend on this sign; the same is true of the other two “field” indices,  and μ. From the relations (148.13) and (148.16), we then find that ∝ and v also are independent of the sign of t.
and μ. From the relations (148.13) and (148.16), we then find that ∝ and v also are independent of the sign of t.
The results obtained enable us to draw some conclusions about the thermodynamic functions of the system for any relationship between t and h. This will be demonstrated for the function η(t, h), which may be written in the form
(for given P). The choice of the first argument of f is determined by the condition (148.12), which separates the cases of weak and strong fields (and we have put β + γ = βδ in accordance with (148.14)); this argument takes all values from small to large. The argument t is always small near the transition point, and must be taken as zero in obtaining the principal term in the function η(t, h). Thus we arrive at the expression
where f is a function of the one argument x = t/h1/βδ. The expression (148.18) is written for h > 0; owing to the symmetry of the system under a simultaneous change of sign of h and η, the formula for h < 0 is obtained from (148.18) by simply substituting —h for h and —η for η.
In strong fields (x « 1), the limiting form (148.10) must be obtained; this means that
Moreover, when h ≠ 0 the order parameter is non-zero both for t > 0 and for t < 0, and t = 0 is not physically distinctive; this means that the function f(x) has an expansion in integral powers of x.
In weak fields when t < 0, the order parameter follows the law (148.5), and for t > 0 we must have η = χh with χ given by (148.8); from these requirements it follows that
The concept of a weak field presupposes that t ≠ 0. For a given non-zero value of t, a zero field is not a singularity of the thermodynamic functions. Hence the function η(t, h) for t ≠ 0 can be expanded in integral powers of the variable h (and the expansion is different for t > 0 and t < 0). A natural formulation of this property would, however, require η(t, h) to be written not in the form (148.18) but in terms of a function of the variable h/tβδ.
Similar considerations can be applied to the correlation function of fluctuations of the order parameter. For instance, in the absence of a field it depends on the parameter t as well as on the distance r. Near the transition point, however, the correlation function G(r; t) can be written as
i.e. in terms of a function of the one variable x = rtv. As x → 0, this function tends to a constant limit, in accordance with the definition (148.7), and as x → 0 it decays exponentially, the correlation radius as a function of temperature being given by (148.6).
PROBLEM
Find the law of temperature dependence as t → 0 for the derivative ∂Cv/∂T if Cp tends to infinity as (148.4) with ∝ > 0.
§ 149 Scale invariance
The relations (148.13)–(148.17) do not involve any assumptions about the nature of the fluctuation pattern near the transition point.† Further conclusions about the critical indices require specific assumptions in this respect.
We may note that the theory in general involves two characteristic dimensions which determine the spatial distribution of the fluctuations: the correlation radius rc and the dimension r0 of the part of the body in which the mean square fluctuation of the order parameter is comparable with its characteristic equilibrium value.‡ The inequality (146.14) which ensures the applicability of the Landau theory may be written rc » r0 (for, according to (146.13) and (146.11), we have, in a volume  and, equating this to η2 ˜ ∝ |t|/b, we find 0 ˜ Tcb/g∝ |t|; comparison with rc (146.12) gives the condition (146.15)). As t → 0, r0 increases more rapidly than rc, and they become comparable at the boundary of the Landau region. The chief assumption about the fluctuation region (this being defined by the opposite inequality to (146.15)) is that the theory here contains no small parameter. In particular, we must everywhere have r0 ˜ rc, so that rc is the only dimension characterising the fluctuations. This is called the hypothesis of scale invariance (L. P. Kadanoff, 1966; A. Z. Patashinskiˇ and V. L. Pokrovskiˇ, 1966).
and, equating this to η2 ˜ ∝ |t|/b, we find 0 ˜ Tcb/g∝ |t|; comparison with rc (146.12) gives the condition (146.15)). As t → 0, r0 increases more rapidly than rc, and they become comparable at the boundary of the Landau region. The chief assumption about the fluctuation region (this being defined by the opposite inequality to (146.15)) is that the theory here contains no small parameter. In particular, we must everywhere have r0 ˜ rc, so that rc is the only dimension characterising the fluctuations. This is called the hypothesis of scale invariance (L. P. Kadanoff, 1966; A. Z. Patashinskiˇ and V. L. Pokrovskiˇ, 1966).
To estimate the fluctuations in the volume  , we can use formula (146.2).§ Substituting in the condition
, we can use formula (146.2).§ Substituting in the condition
the volume 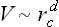 and then expressing χ, rc and η as powers of t according to the definitions of the critical indices, we obtain vd—γ = 2β or, using (148.13),
and then expressing χ, rc and η as powers of t according to the definitions of the critical indices, we obtain vd—γ = 2β or, using (148.13),
By combining this relation with those derived in § 148, we can express all the critical indices in terms of only two independent ones.
The requirement of scale invariance enables us to derive in a uniform way all the relations between the critical indices. To do so, we shall first give a more formal statement of this requirement.
Let the scale of all spatial distances change by the same factor: r — r/u, where u is some constant. Then the scale invariance consists in the assertion that the scales of measurement of t, h and η may be changed in such a way that all the relations in the theory remain unaltered. In other words, we can choose the exponents δt δh, δv (called the scaling dimensions) in the transformations
in such a way that the factor u does not appear in any of the relations.
The change in the spatial scale must, in particular, bring about a similar change in the correlation radius of the fluctuations (rc → rc/u); this ensures that the asymptotic form of the correlation function ˜ exp(−;r/rc) is invariant. According to the definitions (148.6) and (148.11), with h = 0 the correlation radius rc = constant × t—, and with t = 0, rc = constant × h—μ. Applying the transformation (149.3) and the condition that the coefficients in these expressions should remain unchanged, we obtain
Let us next consider the change in the thermodynamic potential due to an infinitesimal change in the field h. According to (144.2),
(with t = constant and, as always, P = constant). In the scale transformation, the volume V → V/ud; with the condition that dϕ is unchanged, i.e. that
we find
Thus the dimensions δt, δh and δη are expressed in terms of the two critical indices μ and v. The requirement of scale invariance of the other relations leads to the expression of the other critical indices in terms of these two.
Let us specify the condition for invariance of the “equation of state” of the system, i.e. the expression of the order parameter in terms of the temperature and the field, η = η(t, h). This means that we must have
The solution of this functional equation has the form
Similar arguments can be applied to the thermodynamic potential Φ(t, h), or more precisely to its singular part, which we shall use Φ below to denote. Being additive, the total thermodynamic potential of the body is proportional to its volume. Hence the requirement of its invariance under the scale transformation may be written
from which
The functions t and ϕ in (149.6) and (149.7) are of course related, since —∂Φ/∂h = ηV. These expressions have been written for h > 0; in view of the symmetry of the effective Hamiltonian under the changes h → —h, η → —η, the formulae for h < 0 are obtained from those given above by making these same changes.†
Similar arguments can be based on (149.7). As already mentioned in connection with (148.18), for a given non-zero h the thermodynamic functions have no singularity with respect to t and must therefore have expansions in integral powers of this variable. This means that, when h ≠ 0 and t → 0, the function ϕ(x) in (149.7) is expanded in integral powers of the small variable x = t/hμ/v. The first terms in this expansion are
where c1 and c2 are constant coefficients. Now, applying the condition that the order parameter and the specific heat, calculated as
should have the forms η ∝ h1/δ and Cp ∝ h—s as t → 0 (these correspond to the strong-field case), we get two relations between the critical indices:
it is easily verified that they in fact follow from the relations derived previously by a different method.
Next, let t be non-zero; then the thermodynamic quantities have no singularity when h passes through zero, and so the function Φ(t, h) can be expanded in integral powers of h. This means that for h → 0 and t ≠ 0 the expansion of the function ϕ(x) in powers of the small variable 1/x = hμ/v/t must have the form
the factor xvd compensates the non-integral power hdμ, and the expansion variable x—v/μ ∝ h. The expansion is, however, different for t > 0 and for t < 0. When t > 0, the potential Φ(t, h) contains only even powers of h, since the derivative —∂Φ/∂h = Vη must be (in the symmetrical phase) an odd function of h:
As h → 0, the specific heat must behave as t—∝, and the order parameter must be η = χh ∝ ht—γ (corresponding to the weak-field case); it is easily seen that the resulting relations are again equivalent to those already known. If the temperature t < 0, then the expansion of Φ(t, h) as h → 0 contains all integral powers of h:
(with, of course, different coefficients c1 and c2).† It is easily verified that the required form (—t)β is obtained for the spontaneous (h-independent) order parameter.
The transformation of the correlation radius has been discussed above. We have still to consider the correlation function of the fluctuations of the parameter η for t → 0 and apply the conditions for scale invariance of the expression
Here it must be assumed that the fluctuating quantities η(r) at different points in space are transformed independently in the same way as the mean value η. It is important that the distances r concerned are small compared with the correlation radius, but large compared with interatomic distances. Then the correlation function is transformed by G → Gu2δη, and we have the condition
This also is a consequence of the relations already known.
Let us finally consider the numerical values of the critical indices. The experimental results and numerical calculations indicate that (in three-dimensional space) the indices a and ζ are quite small: ∝ ˜ 0.1, ζ ˜ 0.05. The first line of the following table gives the values of the other indices found by putting ∝ = ζ = 0 (d = 3). The second line gives the values obtained by taking for α and ζ the values estimated by Wilson’s method (§ 147) for transitions described by an effective Hamiltonian (147.6) with a single order parameter:
§ 150 Isolated and critical points of continuous transition
The curve of phase transitions of the second kind in the PT-plane separates phases of different symmetry, and cannot, of course, simply terminate at some point, but it may pass into a curve of phase transitions of the first kind. A point at which this happens may be called a critical point of a transition of the second kind; it is in some ways analogous to an ordinary critical point. See the point K in Fig. 66; in this and subsequent diagrams, continuous and broken lines represent curves of phase transition points of the first and second kinds respectively.†

FIG. 66
In the Landau theory, the properties of a substance near such a point may be investigated by the method (§ 143) of expansion in powers of the order parameter (L. D. Landau, 1935).
In the expansion (143.3) the critical point is given by the vanishing of the two coefficients A(P, T) and B(P, T); if A = 0 but B > 0 we have a transition of the second kind, and so the curve of such transitions terminates only where B changes sign. For the state of the body at the critical point itself to be stable, it is necessary that the fifth-order term should be identically zero and the sixth-order term should be positive. Thus we start from the expansion
with Acr = 0, Bcr = 0, Dcr > 0 at the critical point.
In the unsymmetrical phase, the minimisation of the thermodynamic potential gives
For the entropy S = — ∂Φ/∂T of this phase we have, omitting terms of higher order in η, S = S0—aη2, where a = ∂A/∂T. A further differentiation gives the specific heat
where only the term whose denominator vanishes at the critical point is shown.
Let T0 = T0(P) be the temperature for which B2—3AD = 0; it is evident that T0 = Tcr when P = Pcr. The first term in the expansion of B2—3AD in powers of T−T0 is
Near the critical point, the difference Tc(P)–T0(P) is a second-order small quantity: since we have A = 0 when T = Tc(P), the difference
and tends to zero as B2 when P → Pcr.
Substitution of (150.4) in (150.3) gives
to the same accuracy, the coefficient in this formula may be taken at Tcr instead of T0. Thus the specific heat of the unsymmetrical phase increases as 1/ (T0—T) as the critical point is approached.
(T0—T) as the critical point is approached.
For states actually on the curve of transitions of the second kind, we find, substituting A = 0 in (150.3) (or (150.5) in (150.6)),
The quantity B is zero at the critical point and is proportional to T−Tcr (or P—Pcr) near that point.
Let us now determine the specific heat of the unsymmetrical phase, on a line of transitions of the first kind but again near the critical point. At points on this line, two different phases (symmetrical and unsymmetrical) are in equilibrium with each other. The value of the parameter η in the unsymmetrical phase is determined by the condition of equilibrium Φ(η) = Φ0, and at the same time we must have ∂Φ/∂η = 0. Substitution of Φ in (150.1) gives the equations
whence
and substitution of this value in the equation Φ(η) = Φ0 then gives
This is the equation of the line of transitions of the first kind.
The specific heat of the unsymmetrical phase on this line is found by simply substituting (150.9) in (150.3):
Comparison with (150.7) shows that the specific heat on the line of transitions of the first kind is twice as great as on the line of transitions of the second kind at the same distance from the critical point. The heat of transition from the unsymmetrical to the symmetrical phase is
We can also show that the curve of transitions of the first kind passes smoothly into the curve of transitions of the second kind at the critical point. On the first curve, the derivative dT/dP is determined by the condition
obtained by differentiating (150.9). The equation of the curve of transitions of the second kind is A = 0, so that dT/dP is determined by the condition dA = 0. At the critical point, A = 0 and B = 0, so that the two conditions coincide and dT/dP has no discontinuity. Similarly, it can be shown that the second derivative d2T/dP2 does have a discontinuity.
As the critical point is approached along the line P = Pc, the specific heat Cp varies as | t|−-1/2 (cf. (150.6)), i.e. the index  . The order parameter in the unsymmetrical phase varies according to η ≅ (— A/3D)1/4 ∝ |t|1/4, i.e. the index β = 1/4. The index v which determines the behaviour of the correlation radius then has the value 1/2, as at any transition point of the second kind in the Landau theory; the vanishing of B does not affect the result in the approximation used to derive (146.8). The values of the remaining indices are derived from (148.13)–(148.17) as γ = 1, δ = 5,
. The order parameter in the unsymmetrical phase varies according to η ≅ (— A/3D)1/4 ∝ |t|1/4, i.e. the index β = 1/4. The index v which determines the behaviour of the correlation radius then has the value 1/2, as at any transition point of the second kind in the Landau theory; the vanishing of B does not affect the result in the approximation used to derive (146.8). The values of the remaining indices are derived from (148.13)–(148.17) as γ = 1, δ = 5,  = μ = 2/5, ζ = 0.
= μ = 2/5, ζ = 0.
We know already that the Landau theory, on which the results given here are based, is inapplicable near a line of transitions of the second kind. It is noteworthy, however, that the conditions for this theory to be valid are more easily satisfied as the critical point is approached, as is seen from the inequality (146.15), where B appears on the right. Of course, the vanishing of B does not mean that there are no fluctuation corrections at the critical point, but the index values given above are in accordance with the scale invariance relation (149.2). It is therefore natural that the fluctuation theory leads only to further logarithmic corrections (which, it may be recalled, are not shown by the values of the indices).
Let us next consider (again in terms of the Landau theory) some properties of points of intersection of lines of phase transition of the first and second kinds.
The symmetry of the unsymmetrical phase in a phase transition of the second kind is determined (as shown in § 145) by the minimisation of the fourth-order terms in the expansion of Φ as functions of the coefficients γi = ηi/η. These terms also depend on P and T, however, and it may happen that the unsymmetrical phase has different symmetries on different parts of the line of transitions. In the simplest such case, we have an intersection of a line of transitions of the second kind (AC in Fig. 67) with one of transitionsof the first kind (BD). The region I is the symmetrical phase; the symmetry groups of phases II and III are sub-groups of that of phase I. They are not, however, in general sub-groups of each other, and therefore the curve BD separating these phases is a line of transitions of the first kind. At B, all three phases are identical.†

FIG. 67
Figure 68 shows a possible type of intersection of several lines of transitions of the second kind. If I is the most symmetrical phase, the symmetry groups of phases II and HI are sub-groups of that of phase I, and that of phase IV is a sub-group of both those of phases II and III.‡

FIG. 68
Finally, it remains to consider the case where the third-order terms in the expansion of the thermodynamic potential do not vanish identically. In this case the condition for the existence of a point of continuous phase transition requires that the coefficients C∝(P, T) of the third-order invariants in the expansion (145.6) should vanish, as well as A(P, T). It is evident that this is possible only if there is not more than one third-order invariant, since otherwise we should obtain more than two equations for the two unknowns P and T. When there is only one third-order invariant, the two equations A(P, T) = 0, C(P, T) = 0 determine pairs of values of P and T, i.e. there are isolated points of continuous phase transition.
Since these points are isolated, they must lie in a certain way at the intersection of curves (in the PT-plane) of phase transitions of the first kind. Since such isolated points of continuous transition have not yet been observed experimentally, we shall not pause to give a detailed discussion here, but simply mention the results.§
The simplest type is that shown in Fig. 69a. Phase I has the higher symmetry, and phases II and III the same lower symmetry, these two phases differing only in the sign of η. At the point of continuous transition (O in Fig. 69) all three phases become identical.

FIG. 69
In more complex cases two or more curves of phase transition of the first kind (e.g. two in Fig. 69b) touch at the point of continuous transition. Phase I has the highest symmetry, phases II and III a lower symmetry, phases IV and V another lower symmetry, these pairs of phases differing only in the sign of η.
§ 151 Phase transitions of the second kind in a two-dimensional lattice
The impossibility of a general theoretical determination of the critical indices lends especial interest to a simple model which allows an exact analytical solution of the problem of phase transitions of the second kind. This is a two-dimensional lattice model, for which the phase-transition problem was first solved by L. Onsager (1944).†
The model considered is a plane square lattice having N points, at each of which is a “dipole” with its axis perpendicular to the lattice plane. The dipole can have two opposite orientations, so that the total number of possible configurations of the dipoles in the lattice is 2N.‡ To describe the various configurations we proceed as follows. To each lattice point (with integral coordinates k, l) we assign a variable σkl which takes two values ±1, corresponding to the two possible orientations of the dipole. If we take into account only the interaction between adjoining dipoles, the energy of the configuration may be written
where L is the number of points in a lattice line, the lattice being regarded as a large square, and N = L2.† The parameter J (> 0) determines the energy of interaction of a pair of adjoining dipoles, which is —J and +J for like and unlike orientations of the two dipoles respectively. Then the configuration with the least energy is the “completely polarised” (ordered) configuration, in which all the dipoles are oriented in the same direction. This configuration is reached at absolute zero; as the temperature increases, the degree of ordering decreases, becoming zero at the transition point, when the two orientations of each dipole become equally probable.
The determination of the thermodynamic quantities requires the calculation of the partition function
taken over all the 2N possible configurations (θ = J/T). The equation
is easily verified by expanding both sides in powers of θ and using the fact that all the  . The expression (151.2) can therefore be written
. The expression (151.2) can therefore be written
where
and x = tanh θ.
The summand in (151.4) is a polynomial in the variables x and σkl. Since each point (k, l) has four neighbours, each σkl can appear in the polynomial in powers from zero to four. After summation over all the σkl = ±1 the terms containing odd powers of σkl vanish, and so a non-zero contribution comes only from terms containing σkl in powers 0,2 or 4. Since  , each term of the polynomial which contains all the variables σkl in even powers gives a contribution to the sum which is proportional to the total number of configurations, 2N.
, each term of the polynomial which contains all the variables σkl in even powers gives a contribution to the sum which is proportional to the total number of configurations, 2N.
Each term of the polynomial can be uniquely correlated with a set of lines or “bonds” joining various pairs of adjoining lattice points. For example, the diagrams shown in Fig. 70 correspond to the terms

FIG. 70
Each line in the diagram is assigned a factor x and each end of each line a factor σkl.
The fact that a non-zero contribution to the partition function comes only from terms in the polynomial which contain all the σkl in even powers signifies geometrically that either 2 or 4 bonds must end at each point in the diagram. Hence the summation is taken only over closed diagrams, which may be self-intersecting (as at the point k, l — 1 in Fig. 70b).
Thus the sum S may be expressed in the form
where gr is the number of closed diagrams formed from an (even) number r of bonds, each multiple diagram (e.g. Fig. 70c) being counted as one.
The subsequent calculation is in two stages: (1) the sum over diagrams of this type is converted into one over all possible closed loops, (2) the resulting sum is calculated by reducing it to the problem of the “random walk” of a point in the lattice.
We shall regard each diagram as consisting of one or more closed loops. For non-self-intersecting diagrams this is obvious; for example, the diagram in Fig. 70c consists of two loops. For self-intersecting diagrams, however, the resolution into loops is not unique: a given diagram may consist of different numbers of loops for different ways of construction. This is illustrated by Fig. 71, which shows three ways of representing the diagram in Fig. 70b as one or two non-self-intersecting loops or as one self-intersecting loop. Any intersection may similarly be traversed in three ways on more complicated diagrams.

FIG. 71
It is easy to see that the sum (151.5) can be extended to all possible” sets of loops if, in computing the number of diagrams gr, each diagram is taken with the sign (—1)n, where n is the total number of self-intersections in the loops of a given set, since when this is done all the extra terms in the sum necessarily cancel. For example, the three diagrams in Fig. 71 have signs +, +, — respectively, so that two of them cancel, leaving a single contribution to the sum, as they should. The new sum will also include diagrams with “repeated bonds”, of which the simplest example is shown in Fig. 72a. These diagrams are not permissible, since some points have an odd number of bonds meeting at them, namely three, but in fact they cancel from the sum, as they should: when the loops corresponding to such a diagram are constructed each bond in common can be traversed in two ways, without intersection (as in Fig. 72b) and with self-intersection (Fig. 72c); the resulting sets of loops appear in the sum with opposite signs, and so cancel. We can also avoid the need to take into account explicitly the number of intersections by using the geometrical result that the total angle of rotation of the tangent in going round a closed plane loop is 2π(l + 1), where l is a (positive or negative) integer whose parity is the same as that of the number v of self-intersections of the loop. Hence, if we assign a factor  to each point of the loop (with the angle of rotation there ϕ = ±1/2π), the product of these factors after going round the whole loop will be (—1)v+1, and for a set of s loops the resultant factor is (—1) n+s, where n = Σv.
to each point of the loop (with the angle of rotation there ϕ = ±1/2π), the product of these factors after going round the whole loop will be (—1)v+1, and for a set of s loops the resultant factor is (—1) n+s, where n = Σv.

FIG. 72
Thus the number of intersections need not be considered if each point on the loop is taken with a factor  and a further factor (— 1)s is taken for the whole diagram (set of loops) in order to cancel the same factor in (—1)n+s.
and a further factor (— 1)s is taken for the whole diagram (set of loops) in order to cancel the same factor in (—1)n+s.
Let fr denote the sum over single loops of length r (i.e. consisting of r bonds), each loop having a factor  at each point on it. Then the sum over all pairs of loops with total number of bonds r is
at each point on it. Then the sum over all pairs of loops with total number of bonds r is
the factor 1/2! takes into account the fact that the same pair of loops is obtained when the suffixes r1 and r2 are interchanged, and similarly for groups of three or more loops. Thus the sum S becomes
Since S includes sets of loops with every total length r1 + r2 + …, the numbers r1, r2, … in the inner sum take independently all values from 1 to ∞.† Hence
and S becomes
This completes the first stage of the calculation.
It is now convenient to assign to each lattice point the four possible directions from it and to number them by a quantity v = 1,2,3,4, say, as follows:

We define as an auxiliary quantity Wr(k, l, v) the sum over all possible paths of length r from some given point k0, l0, v0 to a point k, l, v (each bond having as usual the factor  where ϕ is the change of direction to the next bond); the final step to the point k, l, v must not be from the point to which the arrow v is directed.‡ With this definition, Wr(k0, l0, v0) is the sum over all loops leaving the point k0, l0 in the direction v0 and returning to that point. It is evident that
where ϕ is the change of direction to the next bond); the final step to the point k, l, v must not be from the point to which the arrow v is directed.‡ With this definition, Wr(k0, l0, v0) is the sum over all loops leaving the point k0, l0 in the direction v0 and returning to that point. It is evident that
both sides contain the sum over all single loops, but ΣWr contains each loop 2r times, since it can be traversed in two opposite directions and can be assigned to each of r starting points on it.
From the definition of Wr(k, l, v) we have the recurrence relations
The method of constructing these relations is evident: for example, the point k, l, 1 can be reached by taking the last (r + 1)th step from the left, from below or from above, but not from the right; the coefficients of Wr arise from the factors  .
.
Let Λ denote the matrix of the coefficients in Equation (151.8) (with all k, l) written in the form
The method of constructing these equations enables us to associate with this matrix an intuitive picture of a point moving step by step through the lattice with a “transition probability” per step from one point to another which is equal to the corresponding element of the matrix Λ; its elements are in fact zero except when either k or l changes by ± 1 and the other remains constant, i.e. the point traverses only one bond per step. It is evident that the “probability” of traversing a length r will be given by the matrix Λr. In particular the diagonal elements of this matrix give the “probability” that the poin, will return to its original position after traversing a loop of length r, i.e. they are equal to Wr(k0, l0, v0). Hence
Comparison with (151.7) shows that
where the λi are the eigenvalues of the matrix Λ. Substituting this expression in (151.6) and interchanging the order of summation over i and r, we obtain
The matrix Λ is easily diagonalised with respect to the suffixes k and l by using a Fourier transformation:
Taking Fourier components on both sides of Equation (151.8), we find that each equation contains only Wr(p, q, v) with the same p, q, so that the matrix Λ is diagonal with respect to p and q. For given p, q its elements are
where  ,
,  .
.
For given p, q a simple calculation shows that
Hence, from (151.3) and (151.9), we finally obtain the partition function
The thermodynamic potential is†
or, changing from summation to integration,
(remembering that x = tanh (J/T)).
Let us now examine this expression. The function Φ(T) has a singularity at the value of x for which the argument of the logarithm in the integrand can vanish. As a function of ω1 and ω2, this argument is a minimum for cos ω1 = cos ω2 = 1, when it equals (1 + x2)2—4x(1—x2) = (x2+2x—1)2. This expression has a minimum value of zero for only one (positive) value of x, xc =  2—1; the corresponding temperature Tc (tanh (J/Tc) = xc) is the phase transition point.
2—1; the corresponding temperature Tc (tanh (J/Tc) = xc) is the phase transition point.
The expansion of Φ(t) in powers of t = T—Tc near the transition point includes a singular term as well as the regular part. Here we are interested only in the singular term, the regular part being simply replaced by its value at t = 0. To find the form of the singular term, we expand the argument of the logarithm in (151.12) in powers of ω1, ω2 and t about the minimum; the integral then becomes
where c1 and c2 are constants. Carrying out the integration, we find that the thermodynamic potential near the transition point has the form
where a and b are further constants (with b > 0). The potential itself is continuous at the transition point, but the specific heat becomes infinite in accordance with the formula
which is symmetrical about the transition point.
In this model, the order parameter is represented by the mean dipole moment at the lattice point (the spontaneous polarisation of the lattice), which is non-zero below the transition point and zero above it. The temperature dependence of this quantity can also be ascertained; near the transition point, the order parameter tends to zero according to
(L. Onsager, 1947).†
The correlation function is defined as the mean value of the product of the fluctuations of the dipole moment at two lattice points. The correlation radius is found to tend to infinity as 1/|T—Tc| when T → Tc, and at the point T = Tc itself the correlation function decreases with increasing distance according to
These results, and those of solving the problem of the properties of the same model in an external field, show that the behaviour of the model near the phase transition point satisfies the requirements of the scale invariance hypothesis. The critical indices have the following values:
§ 152 Van der Waals theory of the critical point
It has been noted in § 83 that the critical point of liquid/gas phase transitions is a singularity of the thermodynamic functions of the substance. The physical nature of “this singularity is similar to that which occurs at phase transition points of the second kind: in the latter case it is due to the increased fluctuations of the order parameter, and in the approach to the critical point there are increased fluctuations of the density of the substance. This analogy in the physical nature results in a certain analogy in the possible mathematical description of the two phenomena, to be discussed in § 153.
First, however, let us consider as a necessary preliminary the description of critical phenomena based on neglecting the fluctuations. In such a theory (analogous to the Landau approximation in the theory of phase transitions of the second kind) the thermodynamic quantities for the substance as functions of the variables V and T are assumed to have no singularities, so that they can be expanded in powers of the small changes in these variables. The results given in the rest of this section therefore depend only on the vanishing of the derivative (∂P/∂V)T.
Let us first ascertain the conditions for the substance to be stable when
In deriving the thermodynamic inequalities in § 21, we started from the condition (21.1), which led to the inequality (21.2), which is satisfied if the conditions (21.3), (21.4) hold. The case (152.1) of interest here corresponds to the particular case of the extremum conditions with the equality sign in (21.4):
The quadratic form in (21.2) may now be either positive or zero, depending on the values of δS and δV, and so the question whether E===T0 + P0V has a minimum requires further investigation.
We must obviously examine the case where in fact the equality sign occurs in (21.2):
Using (152.2), this equation may be written
Thus the equation (152.3) implies that we must consider deviations from equilibrium at constant temperature (δT = 0).
At constant temperature the original inequality (21.1) becomes δF + PδV > 0. Expanding δF in powers of δV and making use of the assumption that ∂2F/∂V2 = —(∂P/∂V)T = 0, we find
If this inequality holds for all δV, we must have†
Let us now consider the equation of state of a substance near the critical point. Instead of the variables T and V, it will be more convenient to use the variables T and n, where n is the number of particles per unit volume. We shall also use the notation
In these variables, the conditions (152.1) and (152.4) become
Taking only the first terms in the expansion in powers of small t and η, we write the dependence of pressure on temperature and density in the form
with constant a, b and B. There are no terms in η and η2 in this expansion, from the first two conditions (152.6), and from the third condition B > 0. When t > 0, all states of a homogeneous body are stable (there is nowhere a separation into phases), and we must have (∂p/∂η)t > 0 for all η, whence a > 0. The terms in tη2 and t2η may be omitted, since they are certainly small in comparison with that in tη the term in tη itself must be retained, since it contributes to the derivative
needed below.
The expression (152.7) determines the isotherms of a homogeneous substance near the critical point (Fig. 73). These have a form similar to the van der Waals isotherms (Fig. 19, § 84). When t < 0, they have a minimum and a maximum, and a horizontal section (AD on the bottom isotherm) corresponding to the condition (84.2) gives the equilibrium transition from liquid to gas. Taking V in this condition to be the molecular volume

FIG. 73
we can write the condition as
According to (158.8), the integrand in (152.10) is an odd function of η. It means that η1 = η2. Taking to account that p1 = p2 one gets then from (152.7) the following values for the densities of two phases in equilibrium:
The densities η′1 and η′2 corresponding to the limits of the metastable regions (points B and C in Fig. 73) are given by the condition (∂p/∂η)t, whence†
Substitution of (152.11) makes the sum of the last two terms in (152.7) zero. Hence
is the equation of the curve of equilibrium of liquid and vapour in the pt-plane (and therefore b > 0).‡ According to the Clapeyron-Clausius equation (82.2), the heat of evaporation near the critical point is
It then follows from (152.11) that as t → 0 this heat tends to zero according to
From (16.10) it follows that the specific heat Cp becomes infinite at the critical point while (∂p/∂η)t tends to zero. From (152.8) we find
In particular, for states on the equilibrium curve, η ∝ 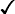 —t and therefore Cp ˜ 1/(—t).
—t and therefore Cp ˜ 1/(—t).
Lastly, let us consider in this theory the density fluctuations near the critical point. The necessary formulae have already been derived in § 116, and to apply them we need only establish the specific form of δFt, the change in the total free energy of the body in a deviation from equilibrium.
where F is the free energy per unit volume and F its mean value, which is constant through the body, and expand F—F in powers of the density fluctuation  (or, equivalently,
(or, equivalently,  ) at constant temperature. The first term in the expansion is proportional to δn, and on integration over the volume it vanishes, since the total number of particles in the body remains unchanged. The second term is†
) at constant temperature. The first term in the expansion is proportional to δn, and on integration over the volume it vanishes, since the total number of particles in the body remains unchanged. The second term is†
Together with this term, which vanishes at the critical point itself, we must also include another term quadratic in δn, due to the inhomogeneity of a body with fluctuating density. Without repeating here the arguments given in § 146, we can state at once that this term is quadratic in the first derivatives of δn with respect to the coordinates; in an isotropic medium, such a term must be the square of the gradient. Thus we arrive at an expression of the form‡
Now expressing δn as a Fourier series (116.9), we can bring this to the form (116.10), with the function
and then, using (116.14), find the Fourier transform of the required correlation function:
since the denominator here is small, the term 1 in v(k) may be neglected. This formula is entirely analogous to (146.8). The correlation function v(r) in the coordinate representation therefore has the same form (146.11), with the correlation radius
In particular, rc ∝ t—1/2 on the critical isochore  .
.
§ 153 Fluctuation theory of the critical point
The formulae derived in § 152 enable us to establish a certain analogy between the thermodynamic description of the properties of a substance near the critical point and near phase transition points of the second kind.
To do so, we proceed in the spirit of the Landau theory by first regarding η not as a definite function of P and T but as an independent variable whose equilibrium value is given by minimising a thermodynamic potential Φ(P, T, η). The latter is to be chosen so that this minimisation in fact gives the correct equation (152.7). The requirement is met by the expression†
Comparing (153.1) and (144.3), we now see that there is an analogy between the description of a phase transition of the second kind in an external field in the Landau theory and the description of a critical point between a liquid and a gas in the van der Waals theory. In the latter case, the order parameter is represented by the change in density of the substance, η = n–nc, and the external field by the difference
If Φ(t, h) is the thermodynamic potential of the body near the phase transition point of the second kind (for some fixed value of the pressure), the expression Φ(t, p–bt) gives the form of the thermodynamic potential near the critical point. The whole of the discussion in § 146 about the change from the potential Φ to the potential ω is valid for any case, and so the analogy applies also to the potentials ω in the two problems.
It has been shown in § 147 how we can go from the thermodynamic potential ω in the Landau theory to the effective Hamiltonian which describes the phase transition in exact fluctuation theory. The analogy mentioned therefore leads us to expect that the laws of behaviour of the thermodynamic quantities near the critical point are the same (with the appropriate change of significance of η and h) as the limiting laws in the fluctuation region of the phase transition of the second kind in an external field (which is described by only one order parameter).
It must be emphasised immediately that this identification can only be approximate. In the theory of phase transitions based on the effective Hamiltonian (147.6), there is an exact symmetry with respect to the transformation h → —h, η → —η) (because of the exact vanishing of the third-order term ˜ η3). In critical-point theory, this symmetry is only approximate; the absence from (153.1) (and therefore from the effective Hamiltonian) of terms which violate this symmetry is due only to neglecting them as small in comparison with the remaining terms. We can therefore assert only that the principal terms in the limiting relationships in the two cases must be the same.†
In the theory of phase transitions with t > 0 and h = 0, we have η = 0; with t < 0 and h → 0, two phases are in equilibrium which have non-zero values η1 and η2 of the order parameter, where η1 = —η2 (the points A and A′ in Fig. 64b, § 144); this equation is an exact consequence of the above-mentioned symmetry of the effective Hamiltonian. For a critical point, the corresponding equation is
which determines the critical isochore (η = 0, i.e. n = nc) for t > 0, and the liquid/vapour equilibrium line for t < 0. The equation η2 = — η1 here signifies the symmetry of the phase equilibrium line in the tη-plane, and an extension of the analogy shows that these values tend to zero as t → 0 according to
with the same exponent as in (148.5).‡ But, since the invariance of the effective Hamiltonian under a change in the sign of η (when h = 0) is only approximate, the question arises of the limiting temperature dependence of the sum η1 + η2. From the foregoing discussion we can say only that it is of a higher order of smallness than η1 and η2 themselves; we shall return to this at the end of the section.
Figure 74 shows the phase diagram in the ηt-plane. The region of separation into two phases is hatched, and its boundary is a symmetrical curve, in accordance with (153.4).

FIG. 74
The heat of evaporation is related to the difference η1−η2 by (152.14). It therefore tends to zero as |t| → 0, by the same law
The general equation of state of a homogeneous substance throughout the neighbourhood of the critical point (in the ηT-plane) may be written
where the two signs correspond to η > 0 and η < 0 (B. Widom, 1965). This formula corresponds to equation (148.18) in the theory of phase transitions (when solved for h).
The same considerations of analyticity apply to f(x) in (153.6) as were discussed in § 149 for transitions of the second kind.
For example, with a given non-zero value of η, a change in the sign of t nowhere causes a passage through the critical point; hence t = 0 is not a singularity of (153.6). This function may therefore be expanded in integral powers of t. Thust(x) is expanded in integral powers of x. The first two terms of this expansion are 1 + c1x, so that the equation of state becomes
the first term in the expansion corresponds to the definition (148.10) for a strong field in the theory of phase transitions. In Fig. 74 the dotted lines show diagrammatically the boundaries of the region to which this equation of state applies. In this region, two further limiting cases may be distinguished. If t « p (in particular, on the critical isotherm, i.e. on the line t = 0), then
If t » p (in particular, on the critical isobar, i.e. on the line p = 0), then
A comparison of (153.8) and (153.9) shows that there is symmetry between p and t, as there should be.†
Similarly, for a given non-zero value of t, the value η = 0 is not a singularity. Hence, for t > 0 and η → 0, the function (153.6) can be expanded in integral powers of η, and the expansion can contain only odd powers, again because of the symmetry of the effective Hamiltonian under a simultaneous change of sign of η and h. From this it follows that‡
the factor xβδ cancels the non-integral power ηδ, and the expansion variable x−β ∝ η. Thus the equation of state becomes
where we have used the equation βδ = β + γ, (148.14). The region where this equation is valid is also shown diagrammatically in Fig. 74. The first term of the expansion (153.10) corresponds to the relation η = χh ∝ ht—γ in the theory of phase transitions in a weak field.
The behaviour of the derivatives of p of various orders with respect to η (with t constant) depends on the direction in the ηt-plane along which the critical point is approached. If the approach is along the critical isotherm (t = 0), the function p(η) is given by (153.8). In practice, the value of δ lies between 4 and 5. Hence not only (∂p/∂η)t but the derivatives of several higher orders tend to zero along the critical isotherm.
If the critical point is approached in any other direction (lying outside the region of separation into two phases, i.e. along a radial line t = constant × |η| with the constant positive), the inequality t » |η|1/β holds, since in practice 1/β > 1. The equation of state then gives
and the second derivative is
The factor η/tβ  1, and tγ—β → 0, since in practice γ > β. Thus the derivative; (∂2p/∂η2)t also tends to zero.
1, and tγ—β → 0, since in practice γ > β. Thus the derivative; (∂2p/∂η2)t also tends to zero.
The behaviour of the specific heat of the substance in the critical region can be ascertained from the expression for the thermodynamic potential,
which is written down immediately by analogy with (149.7) in the theory of phase transitions, with the identical substitution of indices dv = 2—∝, μ/v = 1/(β + γ). Without repeating the whole argument, we can put down at once, by analogy with (149.9) and (149.10), the necessary limiting expressions:†
By twice differentiating (153.12), we find the specific heat on the critical isochore p—bt = 0, t > 0:
Since differentiation with h = 0 and t > 0 signifies differentiation with η = 0, this is the specific heat at constant volume. Thus the specific heat Cv on the critical isochore behaves like Cp in a phase transition of the second kind.
According to (16.10),
As the critical point is approached, the derivative (∂p/∂t)η tends to a constant limit b, as is easily seen from the equation of state (153.7) or (153.10). Hence
The divergence of this expression as the critical point is approached is stronger than that of Cv; the term Cv has therefore been omitted in comparison with Cp.
Lastly, let us consider the asymmetry of the curve of coexistence of phases near the critical point (V. L. Pokrovskiˇ, 1972). As already mentioned, this asymmetry can occur only when terms are taken into account in the effective Hamiltonian which make it no longer symmetrical under the transformation h → —h, → —η. The first such term is† ˜ η2h; its occurrence may be formally regarded as resulting from the replacement of t in the effective Hamiltonian by t+constant×h, so that
This change in the effective Hamiltonian causes a similar change in the thermodynamic potential expressed as a function of h and t:
Near the curve of coexistence of phases, the function ϕ(h, t(is given by (153.13); the required density is found by differentiating with respect to h. The result is
The first term gives the known values (153.4) of the densities on the symmetrical coexistence curve; this term disappears in the sum η1+η2, leaving
which gives the required form. In practice 1 — α > β, so that the asymmetry is in fact relatively slight: (η1+η2)/η1 → 0 as t → 0. The sum η1+η2 is in practice positive; this means that, when it is taken into account, the shape of the coexistence curve is changed in the manner shown in Fig. 75.

FIG. 75
†To simplify the discussion, we shall conventionally speak of the configuration of the atoms or its symmetry as if the atoms were at rest. In reality we should speak of the probability distribution for various configurations of the atoms in space, and of the symmetry of this distribution.
‡Phase transition points of the second kind are also called Curie points, especially when they are associated with a change in the magnetic structure of the body.
§We may note that in this case it can always be assumed that the probability of finding an atom at one of its own sites is greater than at one of the other sites simply because, if it were not, we could transpose the nomenclature of the sites.
†Cases are in principle possible where the occurrence of ordering does not cause a change in the symmetry of the crystal. A phase transition of the second kind is then impossible: even if the transition from the ordered to the disordered state of the crystal were to occur continuously, there would still be no discontinuity of specific heat (see below). In such cases a phase transition of the first kind is, of course, possible.
†It will be recalled that the term “higher symmetry” refers to a symmetry which includes all the symmetry elements (rotations, reflections and translational periods) of the lower symmetry, together with additional elements.
The condition mentioned is necessary but not sufficient for a phase transition of the second kind to be possible; we shall see later that the possible changes of symmetry in such a transition are subject to further restrictions.
‡One exception, for example, is the “lower Curie point” of Rochelle salt, below which the crystal is orthorhombic, but above which it is monoclinic.
†This theory is due to L. D. Landau (1937), who also first showed the general relation between phase transitions of the second kind and the change in the symmetry of the body.
†This condition, however, needs to be made more precise; see the sixth footnote to § 145.
†It can be shown (L. Landau, Zhurnal éksperimental′ no i teoretichesko
i teoretichesko fiziki 7, 627, 1937; translation in Collected Papers of L. D. Landau, p.209, Pergamon, Oxford, 1965) that there is always a third-order term in the expansion for the transition between an isotropic liquid and a solid crystal.
fiziki 7, 627, 1937; translation in Collected Papers of L. D. Landau, p.209, Pergamon, Oxford, 1965) that there is always a third-order term in the expansion for the transition between an isotropic liquid and a solid crystal.
†For example, in a ferromagnet near its Curie point (the transition to the paramagnetic phase), the parameter η is the macroscopic magnetic moment per unit volume, and the field h is the magnetic field; in a ferroelectric, η is the electric dipole moment per unit volume of the body, and h the electric field. In other cases, the field h need not have a direct physical significance, but its formal introduction helps towards a fuller understanding of the properties of the phase transition.
‡In the Landau theory, the equilibrium value of η(P, T) is determined by mini-raising this expansion, i.e. by the condition ∂Φ(P, T, η)∂η = 0. The relation (144.2) is then, of course, satisfied:
†We are everywhere considering transitions for a given value of the pressure; the subscript P indicating that the pressure is constant in the differentiations is omitted for brevity.
†For magnetic transitions, the density ρ(x, y, z) would have to be replaced by the current density j(x, y, z) in the body. In the paramagnetic phase j = 0; beyond the transition point j = δj is small.
†Strictly speaking, this condition should be more accurately stated as follows. The coefficients A(n) depend, of course, on the particular form of the functions  , being quadratic functional of these which depend on P and T as parameters. On one side of the transition point, all these functionals
, being quadratic functional of these which depend on P and T as parameters. On one side of the transition point, all these functionals  ,T} are positive-definite. The transition point is defined as that at which (as P or T varies gradually) one of the A(n) can vanish:
,T} are positive-definite. The transition point is defined as that at which (as P or T varies gradually) one of the A(n) can vanish:
This vanishing corresponds to a definite set of functions  , which may in principle be determined by solving the appropriate variational problem. These will also be the functions
, which may in principle be determined by solving the appropriate variational problem. These will also be the functions  which determine the change bq at the transition point. Substituting these functions in
which determine the change bq at the transition point. Substituting these functions in  ,T} we obtain just the function A(i)(P, T) which satisfies the condition of vanishing at the transition point. The functions
,T} we obtain just the function A(i)(P, T) which satisfies the condition of vanishing at the transition point. The functions  may then be regarded as given, as will be assumed below; the allowance for the variation of the
may then be regarded as given, as will be assumed below; the allowance for the variation of the  with P and T would lead to correction terms of higher order than those of interest here.
with P and T would lead to correction terms of higher order than those of interest here.
†In the language of the theory of representations, this signifies that the symmetric cube [Γ3] of the representation Γ in question must not contain the unit representation. For the (literally) irreducible representations of the space groups, there cannot be more than one third-order invariant (the proof is given by M. S. Shur, Soviet Physics JETP 24, 845, 1967). When two representations are combined as one physically irreducible representation, two third-order invariants may occur.
†It may happen than there is only one fourth-order invariant,  . In this case, the fourth-order term is independent of the γi and higher-order terms must be used to determine the γi; these terms depend on the γi. The use of higher-order terms may also be necessary when the minimisation of the fourth-order terms depending on the γi reduces them to zero.
. In this case, the fourth-order term is independent of the γi and higher-order terms must be used to determine the γi; these terms depend on the γi. The use of higher-order terms may also be necessary when the minimisation of the fourth-order terms depending on the γi reduces them to zero.
‡In § 143 we have considered a transition with a given change of symmetry. Using the concepts defined here, we can say that the quantities γi were assumed to have given values (so that the function δρ had a given symmetry). With the problem stated in these terms, the absence of the third-order term (in the expansion (143.3)) could not be a sufficient condition for the existence of a line of transition points of the second kind, since it does not exclude the possibility that there are third-order terms in the general expansion with respect to several ηi (if the irreducible representation is not one-dimensional). For example, if there are three ηi and the product γ1γ2γ3 is invariant, the expansion of Φ contains a third-order term, whereas this term will vanish if the function δρ has a certain symmetry which requires that one or two γi should be zero.
§The results and examples given below are due to E.M. Lifshitz (1941).
†It must be emphasised, however, that these arguments assume transitions in which the symmetry of the less symmetrical phase is the same along the whole line of transition points, i.e. the value of k0 is independent of temperature. As well as this class of phase transitions (which alone is covered by the discussion in this section), there can also be transitions in which k0 is dependent on temperature and so the periodicity of the less symmetrical phase varies along the line of transition points. Such transitions will be considered elsewhere (see Electrodynamics) in connection with magnetic phase transitions.
†In the language of the theory of representations, this means that the antisymmetric square {Γ2} of the representation Γ in question must not contain the irreducible representations by which the components of a vector are transformed.
†Such a lattice belongs to the symmorphic space group  .
.
†This does not mean, of course, that the change δρ in an actual crystal is given by the function (145.14). Only the symmetry of the expression (145.14) is important.
†The fact that γ1 and γ2 are in each case simply numbers is due to the presence in Φ of only one term (which depends on γ1 and γ2). When there are more fourth-order invariants, the sets of γi that minimise Φ may include some that depend on P and T.
†In this section the thermodynamic potential (Φ, and later Ω) for the body as a whole is denoted by the suffix t; letters without suffixes are used for the potential values per unit volume.
†Here, however, it has to be remembered that the expansion of the coefficient A ≅ ∝t must now be made in powers of the difference t = T—Tc(μ), not T—TC(P); in this sense, the value of the coefficient ∝ = a/V changes.
‡There are no first-order terms in the first derivatives in the expansion of Ω, even when the transition is described by several order parameters. In such cases, the proposition can be verified only by using also the conditions for the stability of the body at the transition point (§ 145).
The theory of fluctuations based on an expression of this type was first developed by L.S. Ornstein and F. Zernicke (1917) for fluctuations near the critical point.
†Analogous results are, of course, obtained on the other side of the transition point, in the unsymmetrical phase. Here  , and the change in the potential Ωt (again as far as quantities ˜ (δη)2) is
, and the change in the potential Ωt (again as far as quantities ˜ (δη)2) is
instead of (146.6). It is clear that the results obtained for  (and for the correlation function below) will differ from the above only in that ∝t is replaced by 2∝ |t|.
(and for the correlation function below) will differ from the above only in that ∝t is replaced by 2∝ |t|.
†This condition can also be verified by a direct calculation of the fluctuation correction to the specific heat of the body near the transition point; see § 147, Problem.
†For transitions described by more than one order parameter, the establishment of all the conditions for the Landau theory to be valid requires more detailed analysis.
‡What is important here is not so much the actual anisotropy of these properties but rather the fact that the deformations cannot be reduced to a single hydrostatic compression. In this sense, the following discussion would also apply to an isotropic solid with a non-zero shear modulus.
§See A. P. Levanyuk and A. A. Sobyanin, JETP Letters 11, 371, 1970.
†This case occurs, in particular, for transitions from the paramagnetic to the ferromagnetic state, where the order parameter is the magnetisation vector of the crystal. A linear dependence of the deformation on the magnetisation is excluded by the requirement of symmetry under time reversal (which leaves the deformation unchanged but changes the sign of the magnetic moment).
‡See A. I. Larkin and S. A. Pikin, Soviet Physics JETP 29, 891, 1969.
§This formulation of the problem for phase transitions of the second kind is due to L. D. Landau (1958).
†To simplify the treatment, we regard the physical quantity  as classical. This assumption is not important, since the long-wavelength variable
as classical. This assumption is not important, since the long-wavelength variable  is certainly classical. For quantum systems, however, it is necessary to satisfy a condition of the form ħ0u « T, where u is the characteristic rate of propagation of oscillations of the order parameter.
is certainly classical. For quantum systems, however, it is necessary to satisfy a condition of the form ħ0u « T, where u is the characteristic rate of propagation of oscillations of the order parameter.
†The theorem stated plays a role here analogous to that of Wick’s theorem in quantum electrodynamics, and the separate terms of the series may be transformed by graphs analogous to Feynman diagrams. An account of the resulting “diagram technique” for calculating the partition function is given by A. Z. Patashinskiˇ and V, L. Pokrovskiˇ, Fluctuation Theory of Phase Transitions, Pergamon Press, Oxford, 1979
†Such a distinguishing is possible in the formal problem of a phase transition in four-dimensional space (in which case the integrals diverge logarithmically as t → 0). This is the basis of a method proposed by K. G. Wilson (1971) for estimating the critical indices, which are calculated for the case of a space of 4— dimensions (where
dimensions (where  is small), the result then being extrapolated to
is small), the result then being extrapolated to  = 1.
= 1.
†The impossibility of infinite Cv on the transition line is also evident from the fact that it would lead to Cv = T(dVc/dT)2 (∂P/∂V)T (cf. (143.14)), which is certainly impossible, as Cv is positive and (∂P/∂V)T is negative. The specific heat Cv has, however, an infinite derivative on the transition line (see Problem).
†The Landau theory corresponds to the following values of the critical indices:
†It is therefore not surprising that all these relations are satisfied in the Landau theory also.
‡This discussion refers, of course, only to the distribution at distances large compared with atomic dimensions.
§In this form (i.e. expressed in terms of the susceptibility χ) this formula is general and does not depend on the assumptions made in the Landau theory, as mentioned after (146.2).
 In the Landau theory there is no scale invariance, and equation (149.2) is therefore invalid.
In the Landau theory there is no scale invariance, and equation (149.2) is therefore invalid.
†It may be mentioned once more, however, that in the effective Hamiltonian η appears as a variable over which the continuum integration is taken in the integral over states. In the thermodynamic formulae, η is the equilibrium value of the order parameter, which is given by the derivative ∂Φ/∂h (or ∂Ω/∂h) of the thermodynamic potential determined from the integral over states. The symmetry of the effective Hamiltonian leads, of course, to an analogous symmetry in the thermodynamic relations.
†If (149.10) relates, say, to fields h > 0, the formula for h < 0 is obtained from it by the substitution h → —h. It may be recalled (see § 144) that for t < 0 the states in fields of opposite sign refer to physically identical “phases” differing in the sign of the order parameter (both spontaneous and field-induced); as h → 0, the two phases are in equilibrium with each other.
†The term tricritical point is also used in the literature for a point such as K.
†The fluctuation corrections may probably cause a singularity at B, the curves AB and CB forming a cusp.
‡A point of intersection of the type shown in Fig. 67 is called bicritical in the literature, and one as in Fig. 68 tetracritical.
§See L. Landau, Zhurnal éksperimental’noˇ teoreticheskoˇ fiziki 7, 19, 1937; translation in Collected Papers of L. D. Landau, p. 193, Pergamon, Oxford, 1965.
†The original method used by Onsager was extremely complex. Later, various authors simplified the solution. The method described below (which in part makes use of certain ideas in the method of M. Kac and J. C. Ward (1952)) is due to N. V. Vdovichenko (1964).
‡This model is known as the Ising model; it was in fact first used by W. Lenz (1920) and was studied by E. Ising (1925) for the one-dimensional case (in which there is no phase transition).
†The number L is, of course, assumed macroscopically large, and edge effects (due to the special properties of points near the edges of the lattice) will be neglected throughout the following discussion.
†Loops with more than N points make no contribution to the sum, since they must necessarily contain repeated bonds.
‡In fact Wr(k, l, v) depends, of course, only on the differences k—k0, l—l0.
†In the model under discussion the temperature affects only the ordering of dipole orientations, not the distances between dipoles (the “thermal expansion coefficient” of the lattice is zero). It is then immaterial whether we consider the free energy or the thermodynamic potential.
†A comparatively simple method of solving this problem is given by N. V. Vdovichenko, Soviet Physics JETP 21, 350, 1965.
†As regards the critical indices, a logarithmic increase corresponds to a zero exponent (see after (148.7)).
†It may be noted that the case of equality in (21.3) is impossible in this discussion, since the condition (21.4) would then be violated. The simultaneous vanishing of the two expressions (21.3) and (21.4) is also impossible: if we add a further condition to the vanishing of (∂P/∂V)T and (∂2P/∂V2)T, there result three equations in two unknowns, which in general have no common solution.
†In a theory which takes account of the singularity of the thermodynamic quantities at the boundary of the metastable states, there is no curve BC.
‡When t > 0, equation (152.13) determines the critical isochore, the curve of constant density (η = 0) passing through the critical point.
†Since the free energy F is referred to a fixed (unit) volume of substance, not to a fixed number of particles in it, (∂F/∂n)T = μ. The second derivative is
since, for T = constant, dμ = v dP, where v = 1/n is the molecular volume.
‡The fact that δFt is expressed as an integral of a function of a point in the body (not of two points as in the general expression (116.8)) results from the assumption that δn varies slowly; the long-wavelength components of the density fluctuations are considered.
†The (here unimportant) coefficient of the square bracket is chosen so that after minimisation the expression (153.1) gives the correct potential Φ(P, T). It may seem strange that (153.1) is not symmetrical in p and t, in that the coefficient of η2 does not involve p. In reality, the η2 term is significant only if the coefficient p—bt of η is small, and in that case we can equally well write atη2 or apη2/b.
†The analogy described must not, of course, conceal the physical difference between the two phenomena: for a phase transition of the second kind, we have a whole curve of transition points, which separates (in the PT-plane) the regions of existence of two phases with different symmetry. A critical point, however, is an isolated point (at the end of an equilibrium curve) in the phase diagram of two phases having the same symmetry.
‡Here and in the rest of § 153, when referring to the critical indices for transitions of the second kind, we mean specifically the values of these indices for transitions described by only one order parameter, with an effective Hamiltonian of the form (147.6). The van der Waals theory of the critical point corresponds to the values of the indices given for the Landau theory in the footnote to (148.11).
†For t ∝ ηδ, the argument of f(x) in (153.6) is x ∝ t/t1/βδ « 1, since in practice βδ = β+γ > 1. This proves that the case t » p is in fact possible in the equation of state (153.7).
‡The case x → — ∞ is not realistic, since values of |η|1/β « |t| with t < 0 are in the region of separation.
†It may be recalled that Φ here denotes (as in § 149) the singular part of the thermodynamic potential. While it is a small correction to the principal (non-singular) part, it also gives a similar correction to the other thermodynamic potentials. On the phase equilibrium curve, the characteristic magnitude of this correction is ∝ t2—∝, a point that will be made use of in § 154.
†The inclusion in the effective Hamiltonian of a term ˜ η3t would not destroy the symmetry, since such a term could be eliminated by simply applying a transformation η → η+constant×t. In this connection it may be recalled (cf. the footnote following (149.7)) that η in the effective Hamiltonian is only a continuum integration variable, and therefore the transformation mentioned does not affect the integral over states.






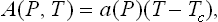






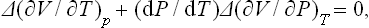







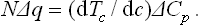





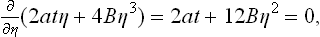






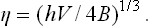







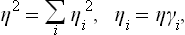




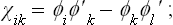













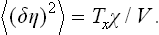



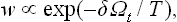
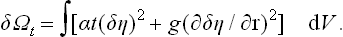
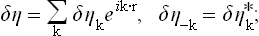












 is given by
is given by