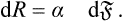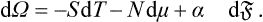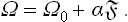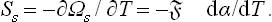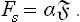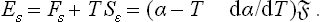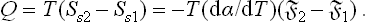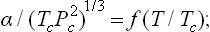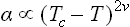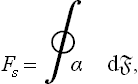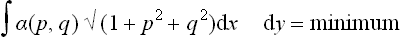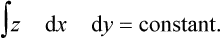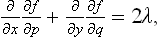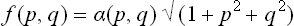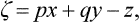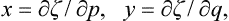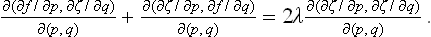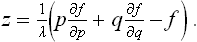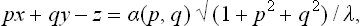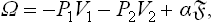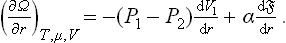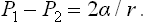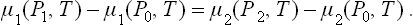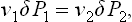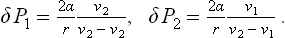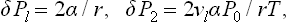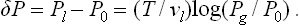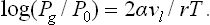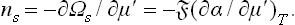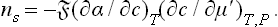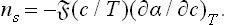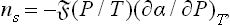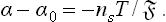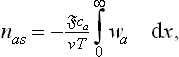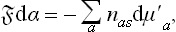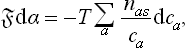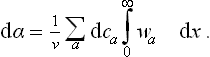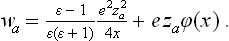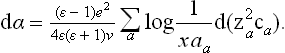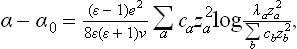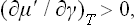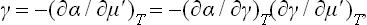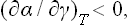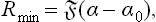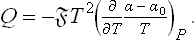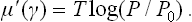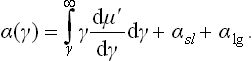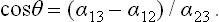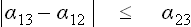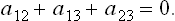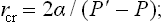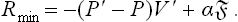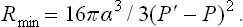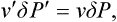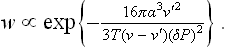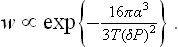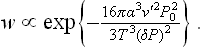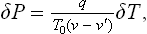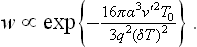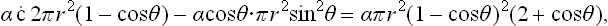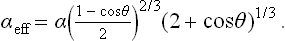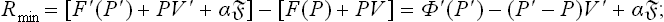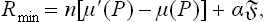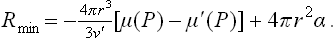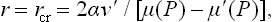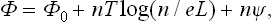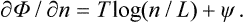SURFACES
Publisher Summary
As the size of a body, that is, the number of particles in it increases, the surface effects increase much more slowly than the volume effects. There are a number of phenomena that depend on the properties of surfaces of separation. The thermodynamic properties of such an interface are described by one quantity, a function of the state of the bodies. The law of corresponding states can be qualitatively applied to the surface tension between a liquid and its vapour. At a critical point, the liquid and gas phases become identical, the interface between them ceases to exist, and the surface tension coefficient must become zero. The surface tension of an anisotropic body, a crystal, is different at different faces; it may depend on the direction of the face, that is, on its Miller indices.
§ 154 Surface tension
HITHERTO we have entirely neglected effects resulting from the presence of surfaces of separation between different bodies.† Since, as the size of a body (i.e. the number of particles in it) increases, surface effects increase much more slowly than volume effects, the neglect of surface effects in the study of volume properties of bodies is entirely justified. There are, however, a number of phenomena which depend in fact on the properties of surfaces of separation.
The thermodynamic properties of such an interface are entirely described by one quantity, a function of the state of the bodies, defined as follows. We denote by 
the area of the interface, and consider a process whereby this area undergoes a reversible change by an infinitesimal amount d. The work done in such a process is obviously proportional to d, and so can be written as
The quantity a thus defined is a fundamental characteristic of the interface, and is called the surface-tension coefficient.
Formula (154.1) is exactly analogous to the formula dR = — P dV for the work done in a reversible change in the volume of a body. We may say that α plays the same part in relation to the surface as the pressure does in relation to the volume. In particular, we can easily show that the force on unit length of the perimeter of any part of the interface is equal in magnitude to α and is directed tangentially to the surface and along the inward normal to the perimeter.
Here we have assumed that α is positive. The fact that it must indeed always be positive is shown by the following argument. If α < 0, the contour bounding the surface would be subject to forces along the outward normal, i.e. tending to “stretch” the surface; the interface between two phases would therefore tend to increase without limit, and the phases would mix and cease to exist separately. If α > 0, on the other hand, the interface tends to become as small as possible (for a given volume of the two phases). Hence, for example, if one isotropic phase is surrounded by another, it will take the form of a sphere (the effect of an external field, e.g. gravity, being neglected, of course).
Let us now consider in more detail the surface tension at the interface between two isotropic phases, liquid and vapour, of the same substance. If an interface between two phases in equilibrium is concerned, it must be remembered that their pressure and temperature are in a definite functional relation given by the equation of the phase equilibrium curve, and α is then essentially a function of only one independent variable, not of two.
When surface effects are neglected, the differential of the energy of a system of two phases (of the same substance), for a given total volume V of the system, is dE = T dS+μ dN; in equilibrium, the temperatures T and chemical potentials μ of the two phases are equal, and this equation can therefore be written for the whole system. When the presence of surface effects is taken into account, the right-hand side of the equation must clearly include also the expression (154.1):
It is, however, more convenient to take as the fundamental thermodynamic quantity not the energy but the potential ω, the thermodynamic potential in terms of the independent variables T and μ (and the volume V). The convenience of ω in this case arises because T and μ are quantities which have equal values in the two phases, whereas the pressures are not in general equal when surface effects are taken into account; see § 156. For the differential dω, again with V = constant, we have
The thermodynamic quantities (such as E, ω and S) for the system under consideration can be written as the sum of a “volume” part and a “surface” part. This division, however, is not unique, since the number of particles in each phase is indeterminate to the extent of the number of particles in the transition layer between the phases; the same is true of the volumes of the phases. This indeterminacy is of just the same order of magnitude as the surface effects with which we are concerned. The division can be made unique if the following reasonable condition is imposed: the volumes V1 and V2 of the two phases are defined so that, in addition to the equation V1+V2 = V, where V is the total volume of the system, the equation n1V1+n2V2 = N is satisfied, where N is the total number of particles in the system, and n1 = n1(μ, T) and n2 = n2(μ, T) are the numbers of particles per unit volumein each phase (the phases being regarded as unbounded).
These two equations determine the choice of the volumes V1 and V2 (and the numbers of particles N1 = n1V1, N2 = n2V2), and hence also the volume parts of all other thermodynamic quantities. We shall denote volume parts by the suffix 0, and surface parts by the suffix s; by definition, Ns = 0.
From (154.3) we have, for constant T and μ (and therefore constant α), dω = α d; it is therefore evident that ωs = α, and so
Since the entropy S = —(∂Ω/∂T)μ,, the surface part of it is†
Next, let us find the surface free energy; since F = ω +Nμ and Ns = 0,
The surface energy is
The quantity of heat absorbed in a reversible isothermal change of surface area from 1 to 2 is
The sum of the heat Q and the work R = α(§2—1) in this process is equal to the change in energy Es2—Es1, as it should be.
The law of corresponding states (§ 84) can be qualitatively applied to the surface tension between a liquid and its vapour. From this law we should expect that the dimensionless ratio of α to a quantity with dimensions erg/cm2 formed from the critical temperature and critical pressure will be a universal function of the reduced temperature T/Tc:
at temperatures well below the critical value, this ratio is approximately 4.
At a critical point, the liquid and gas phases become identical, the interface between them ceases to exist, and the surface tension coefficient must become zero. Using the ideas of the fluctuation theory of the critical point, we can express the manner of its tending to zero in terms of the critical indices defined in § 148.
As the critical point is approached, the width of the transition layer between the two phases increases and becomes of macroscopic size. Sufficiently close to the critical point, it must be of the order of the correlation radius rc of the fluctuations. In order to find the surface tension, we need only now multiply the width rc by the characteristic thermodynamic potential density, or rather its singular part, which determines the critical phenomena. This density is ∝ (–t)2-α; see the footnote to (153.12).† Thus the surface tension coefficient is ∝ rc(–t)2-α; since rc ∝ (–t)−v from (148.6), and 2–α = vd = 3v from (149.2), we have finally
(B. Widom, 1965). In practice, 2v ≅ 1.3.‡
§ 155 Surface tension of crystals
The surface tension of an anisotropic body, a crystal, is different at different faces; it may be said to depend on the direction of the face, i.e. on its Miller indices. The form of this dependence is somewhat unusual. Firstly, the difference in the values of α for two crystal planes with arbitrarily close directions is itself arbitrarily small, i.e. the surface tension can be represented as a continuous function of the direction of the face. It can nevertheless be shown that this function nowhere has a definite derivative. For example, if we consider a set of crystal planes intersecting along a common line, and denote by ϕ the angle of rotation around this line, which defines the direction of the plane, we find that the function α = α(ϕ) has two different derivatives for every value of ϕ, one for increasing and the other for decreasing values of the argument.§
Let us suppose that the surface tension is a known function of the direction of the faces. The question arises how this function can be used to determine the equilibrium form of the crystal. (It must be emphasised that the crystal shape observed under ordinary conditions is determined by the conditions of growth of the crystal and is not the equilibrium shape.) The equilibrium form is determined by the condition for the free energy F to be a minimum (for given T, μ and volume V of the crystal) or, what is the same thing, by the condition for its surface part to be a minimum. The latter is
the integral being taken over the whole surface of the crystal; for an isotropic body α = constant, Fs = α, and the equilibrium form is determined simply by the condition for the total area to be a minimum, i.e. it is a sphere.
Let z = z(x, y) be the equation of the surface of the crystal, and let p = ∂z/∂x, q = ∂z/∂y denote the derivatives which determine the direction of the surface at each point; α can be expressed as a function of these, α = α(p, q). The equilibrium form is given by the condition
with the added condition of constant volume
This variational problem leads to the differential equation
where
and λ is a constant.
Next, we have by definition dz = p dx + q dy; with the auxiliary function
we find dζ = x dp + y dq or
ζ being here regarded as a function of p and q. Writing the derivatives with respect to x and y in (155.3) as Jacobians, multiplying both sides by ∂(x, y)/∂(p, q) and using (155.6), we obtain the equation
This equation has an integral f = λζ = λ(px+qy—z), or
This is just the equation of the envelope of the family of planes
where p and q act as parameters.
This result can be expressed in terms of the following geometrical construction. On each radius vector from the origin we mark off a segment ot length proportional to α(p, q), where p and q correspond to the direction of that radius vector.† A plane is drawn through the end of each segment af right angles to the radius vector; then the envelope of these planes gives the equilibrium form of the crystal (G. V. Vul’f).
It can be shown‡ that the unusual behaviour of the function α mentioned at the beginning of this section may have the result that the equilibrium form of the crystal determined by this procedure will include a number of plane areas corresponding to crystal planes with small values of the Miller indices. The size of the plane areas rapidly decreases as the Miller indices increase. In practice this means that the equilibrium shape will consist of a small number of plane areas which are joined by rounded regions instead of intersecting at sharp angles.
§ 156 Surface pressure
The condition that the pressures of two phases in contact are equal has been derived (in § 12) from the equality of the forces exerted on the interface by the two phases; as elsewhere, surface effects were neglected. It is clear, however, that if the interface is not plane a displacement of it will in general change its area and therefore the surface energy. In other words, the existence of a curved interface between the phases leads to additional forces, as a result of which the pressures of the two phases will not be equal. The difference between them is called the surface pressure.
This quantity is determined by the condition of mechanical equilibrium: the sum of the forces acting on each phase at the interface should be zero. This sum is in turn given by the derivative of a thermodynamic potential with respect to the displacement of the interface, the other variables corresponding to this potential remaining constant; cf. (11.3) and (15.11). In particular, in differentiating the potential Ω we must regard P, μ and the total volume of the system as constants.
Let us consider two isotropic phases (two liquids, or a liquid and a vapour). We shall assume that one of the phases (phase 1) is a sphere (of radius r) surrounded by the other phase. Then the pressure is constant within each phase, and the total thermodynamic potential ω of the system is
the first two terms forming the volume part of the potential; the suffixes 1 and 2 refer to the two phases.
The pressures, of the two phases satisfy the equations μ1(P1, T) = μ2(P2, T) ≡ μ, where μ is the common value of the two chemical potentials. Hence, for constant μ and T, we must regard P1 and P2 as constant also, and likewise the surface-tension coefficient α. Since V = V1+V2 is constant, we find as the condition of mechanical equilibrium
Finally, substituting V1 = 4πr3,/3 = 4πr2, we obtain the required formula:
For a plane interface (r → ∞) the two pressures are equal, as we should expect.
Formula (156.2) determines only the difference between the pressures in the two phases. We shall now calculate each of them separately.
The pressures P1 and P2 satisfy the equation μ1(P1, T) = μ2(P2, T). The common pressure P0 in the two phases when the interface is plane is determined at the same temperature by the relation μ1(P0, T) = μ2(P0, T). Subtraction of these two equations gives
Assuming that the differences ΔP1 = P1—P0, ΔP2 = P2—P0 are relatively small and expanding the two sides of equation (156.3) in terms of ΔP1 and ΔP2, we find
where v1 and v2 are the molecular volumes (see (24.12)). Combining this with formula (156.2) written in the form ΔP1—ΔP2 = 2α/r, we find the required ΔP1 and ΔP2 as
For a drop of liquid in a vapour, v1 « v2; regarding the vapour as an ideal gas, we have v2 = 7/P2 ≅ T/P0, and so
where for clarity the suffixes l and g are used in place of 1 and 2. Thus we see that the vapour pressure over the drop is greater than the saturated vapour pressure over a plane liquid surface, and increases with decreasing radius of the drop.
When the drop is sufficiently small and ΔPg/P0 is no longer small, formulae (156.6) become invalid, since the large variation of the vapour volume with pressure means that the expansion used to derive (156.4) from (156.3) is no longer permissible. For a liquid, whose compressibility is small, the effect of a change of pressure is slight, and the left-hand side of (156.3) can again be replaced by vl ΔPl. On the right-hand side we substitute the chemical potential of the vapour in the form μ = T log Pg + χ(T), obtaining
Since in this case ΔPl » ΔPg, the difference Pl—P0 can be replaced by Pl—Pg; using formula (156.2) for the surface pressure, we then have finally
For a bubble of vapour in a liquid we similarly obtain the same formulae (156.6), (156.7) but with the opposite signs.
§ 157 Surface tension of solutions
Let us now consider an interface between a liquid solution and a gas phase (a gas and a solution of it in a liquid, a liquid solution and its vapour, etc.).
As in § 154, we divide all thermodynamic quantities for the system under consideration into volume and surface parts, the manner of division being determined by the conditions V = V1 + V2, N = N1 + N2 for the volume and number of solvent particles. That is, the total volume V of the system is divided between the two phases in such a way that, on multiplying V1 and V2 by the corresponding numbers of solvent particles per unit volume, and adding, we obtain just the total number N of solvent particles in the system. Thus by definition the surface part Ns = 0.
As well as other quantities, the number of solute particles will also be written as a sum of two parts, n = n0 + ns. We may say that n0 is the quantity of solute which would be contained in the volumes V1 and V2 if it were distributed in each with a constant concentration equal to the volume concentration of the corresponding solution. The number n0 thus defined may be either greater or less than the actual total number n of solute particles. If ns = n—n0 > 0, this means that the solute accumulates at a higher concentration in the surface layer (called positive adsorption). If ns < 0, the concentration in the surface layer is less than in the volume (negative adsorption).
The surface-tension coefficient of the solution is a function of two independent variables, not one. Since the derivative of the potential ω with respect to the chemical potential is minus the corresponding number of particles, ns can be found by differentiating Ωs = α with respect to the chemical potential μ′ of the solute:†
Let us assume that the pressure of the gas phase is so small that its effect on the properties of the liquid phase may be neglected. Then the derivative of α in formula (157.1), which must be taken along the phase equilibrium curve at the temperature concerned, can be replaced by the derivative at constant (viz. zero) pressure (and constant T). Regarding α as a function of the temperature and the concentration c of the solution, we can rewrite formula (157.1) as
According to the thermodynamic inequality (96.7), the derivative (∂μ′/∂c)T, P is always positive. Hence it follows from (157.2) that ns and (∂α/∂c)T have opposite signs. This means that, if the solute raises the surface tension (α increases with increasing concentration of the solution), it is negatively adsorbed. Substances which lower the surface tension are positively adsorbed.
If the solution is a weak one, the chemical potential of the solute is of the form μ′ = T log c + ψ(P, T); substituting this in (157.2), we find
A similar formula,
is obtained for the adsorption of a gas (at pressure P) by a liquid surface.
If not only the solution but also the adsorption from it is weak, α can be expanded in powers of c; we have approximately α = α0 + α1c, where α0 is the surface tension at the interface between two phases of pure solvent. Then we have from (157.3) α1 = —nsT/c, and hence
The resemblance between this formula and van’t Hoff’s formula for the osmotic pressure should be noticed (the volume being here replaced by the surface area).
§ 158 Surface tension of solutions of strong electrolytes
The change in surface tension of a liquid when a strong electrolyte is dissolved in it can be calculated in a general form for weak solutions (L. Onsager and N. N. T. Samaras, 1934).
Let wa(x) denote the additional energy of an ion (of the ath kind) because of the free surface at a distance x from the ion (wa(x) tending to zero as x → ∞). The ion concentration near the surface differs from its value ca within the solution by a factor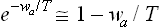 
. The contribution of the surface to the total number of these ions in the liquid is therefore
where v is the molecular volume of the solvent.
To calculate the surface tension, we begin from the relation
where the summation is over all the kinds of ion in the solution. For weak solutions (μ′a = T log ca + ψa),
Substitution of (158.1) gives
It will be seen from the subsequent results that the main contribution to the integral comes from distances x which are large compared with the distances between molecules but small compared with the Debye length 1/x.
The energy wa consists of two parts:
The first term arises from the “image force” on a charge eza in a medium with dielectric constant ε at a distance x from its surface. Since x « 1/x, the screening effect of the ion cloud round the charge does not alter this energy. In the second term, ϕ(x) denotes the change (owing to the presence of the surface) in the field potential due to all the other ions in the solution. This term is unimportant here, however, since it disappears on substituting (158.5) in (158.4) because of the electrical neutrality of the solution (Σcaza = 0, and therefore Σza dca = 0).
Thus, carrying out the integration in (158.4), we find
The logarithmic divergence of the integral at both limits confirms the statement made above concerning the range of integration; we have naturally taken as the upper limit the screening length 1/x, and as the lower limit a quantity aa of the order of atomic dimensions, but different for the different kinds of ion. Since x2 is proportional to the sum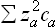 
,† we see that expression obtained is a total differential and so can be integrated directly, giving
where α0 is the surface tension of the pure solvent and the λa are dimensionless constants.
This formula gives the solution of the problem. It should be noticed that the dissolution of a strong electrolyte increases the surface tension of the liquid.
§ 159 Adsorption
Adsorption in the restricted sense includes cases where the solute is concentrated at the surface of a solid or liquid adsorbent,‡ and hardly any of it enters the volume of the adsorbent. The adsorbed film thus formed can be described by the surface concentration γ, defined as the number of particles of the adsorbate (adsorbed substance) per unit surface area. At low pressures of the gas from which adsorption occurs, the concentration γ must be proportional to the pressure;§ at high pressures, however, γ increases less rapidly and tends to a limiting value corresponding to the formation of a monomolecular layer with the adsorbate molecules closely packed together.
Let μ′ be the chemical potential of the adsorbate. By the same method as was used in § 96 for ordinary solutions we can derive for adsorption the thermodynamic inequality
which is entirely analogous to (96.7). From (157.1) we have
and (159.1) therefore implies that
i.e. surface tension decreases as the surface concentration increases.
The minimum work which must be done to form the adsorbed film is equal to the corresponding change in the thermodynamic potential ω:
where α0 is the surface tension on the surface before adsorption. Hence, using (91.4), we find the heat of adsorption
The adsorbed film may be regarded as a kind of two-dimensional thermodynamic system, which may be either isotropic or anisotropic, despite the isotropy of the two volume phases.† The question arises of the possible types of symmetry of the film.
At the end of § 137, we have already mentioned that, although the existence of a two-dimensional crystal lattice of arbitrarily great extent is impossible (since it is smoothed out by thermal fluctuations), a film may still show solid-crystal properties if it is of relatively small size. But the smoothed-out structure is still anisotropic, as noted at the end of § 138. Such an anisotropic film can have only an axis of symmetry perpendicular to its plane, and planes of symmetry passing through this axis. The only possible types of symmetry for such systems are therefore the point groups Cn and Cnv.
As with three-dimensional solids, different phases can exist in two-dimensional films. The equilibrium conditions for two phases in a film require the equality of their surface tensions as well as their temperatures and chemical potentials. The condition on the surface tensions corresponds to the condition of equal pressures in three-dimensional phases, and simply expresses the necessity for the forces exerted by each phase on the other to balance.
§ 160 Wetting
Let us consider adsorption on the surface of a solid from a vapour at a pressure close to the saturation value. The equilibrium concentration γ is determined by the condition that the chemical potential of the adsorbate μ′ is equal to that of the vapour μg. Various cases can occur according to the dependence of μ′ on γ.
Let us suppose that the quantity of adsorbate gradually increases and the adsorbed layer becomes a liquid film of macroscopic thickness. The surface concentration γ then becomes a conventionally defined quantity proportional to the film thickness l: γ = 
l/m, where m is the mass of a molecule and the density of the liquid. As the film thickness increases, the chemical potential of the substance forming it tends to μl, the chemical potential of the liquid in bulk. We shall measure the value of μ′ (for given P and T) from this limiting value, i.e. write μ′ + μl in place of μ′; thus, by definition, μ′ → 0 as γ → ∞.
The chemical potential of the vapour can be written as μg = μl(T) + T log (P/P0), where P0(T) is the saturated vapour pressure; here we have used the fact that the saturated vapour is, by definition, in equilibrium with the liquid, i.e. we must have μg = μl when P = P0.† The surface concentration is determined by the condition μ′ + μl = μgs, or
If this equation is satisfied by several values of γ, the one which corresponds to a stable state is that for which the potential Ωs is a minimum. Taking the value per unit area of the surface, we obtain a quantity which may be called (in the general case of any film thickness) the “effective surface-tension coefficient” α at the solid-vapour boundary, and which takes into account the presence of the layer between them. Integrating the relation (159.2), we can write
The constant is so chosen that as γ → ∞ the function α(γ) becomes the sum of the surface tensions at the “bulk”-phase (solid-liquid and liquid-gas) interfaces.
It may also be recalled that a necessary condition for the thermodynamic stability of a state is the inequality (159.1), which is valid for any γ.
Let us now consider some typical cases which may occur, depending on the nature of the function μ′(γ). In the diagrams given below, the continuous curve shows the form of this function in the region of macroscopically thick films of liquid, while the broken curve is that for adsorbed films of “molecular” thickness. It is, of course, not strictly possible to represent the function in these two regions in one diagram to the same scale, and to this extent the diagrams are a convention.
In the first case shown (Fig. 76a) the function μ′(γ) decreases monotonically with increasing γ (i.e. with increasing film thickness) in the range of macroscopic thicknesses. For molecular dimensions the function μ′(γ) always tends to — ∞ as T log γ when γ → 0, this law corresponding to a “weak solution” of the adsorbate on the surface. The equilibrium concentration is determined, according to (160.1), by the point of intersection of the curve with a horizontal line μ′ = constant ≤ = 0. In this case, this can occur only at molecular concentrations, i.e. ordinary molecular adsorption must occur, as discussed in § 159.
FIG. 76
μ′(γ) increases monotonically but is everywhere negative (Fig. 76b), then in equilibrium a liquid film of macroscopic thickness is formed on the surface of the adsorbent. In particular, when the pressure P = P0 (saturated vapour), the film formed must be so thick that the properties of the substance in it do not differ from those of the liquid in bulk, i.e. the saturated vapour must be in contact with its own liquid phase. In that case we say that the liquid completely wets the solid surface in question.
More complicated cases are also thoretically possible. For example, if the function μ′(γ) passes through zero and has a maximum (Fig. 76c) we have a case of wetting but with formation of a film stable only at thicknesses below a certain limit. The film of finite thickness corresponding to the point A is in equilibrium with the saturated vapour. This state is separated from the other stable state (equilibrium of the solid wall with the bulk liquid) by a metastable region AB and a region of complete instability BC.
The type of curve shown in Fig. 76d corresponds to a film which is unstable over a certain range of thickness. The line BF which cuts off equal areas BCD and DEF joins points B and F which have equal values of α (and equal μ′), as is easily seen from (160.2). The branches AB and FG correspond to stable films; the range CE is completely unstable, while BC and EF are metastable.
The two boundaries of the instability range (the points B and F) correspond in this case to macroscopic film thicknesses. Instability in the range from a certain macroscopic thickness to molecular thicknesses would correspond to a curve of the type shown in Fig. 76e, but such a curve would more likely lead to non-wetting, since the limit of stability would correspond to a point on BC where a horizontal line cuts off equal areas below the upper part and above the lower part of the curve. But this is usually impossible, since the latter area, which is related to the van der Waals forces (see below), is small compared with the former, which is related to the considerably greater forces at molecular distances. This means that the surface tension everywhere on BC is greater than that which would correspond to molecular adsorption on a solid surface, and the film will therefore be metastable.
The chemical potential of the liquid film (measured from μl) represents the difference between the energy of the substance in the film and that in the bulk liquid. It is therefore clear that μ′ is determined by the interaction forces between atoms at distances large compared with atomic dimensions and ˜ l(van der Waals forces). The potential μ′(l) can be calculated in a general form, the result being expressed in terms of the permittivities of the solid wall and the liquid (see Part 2).
§ 161 The angle of contact
Let us consider three bodies in contact, solid, liquid and gas (or one solid and two liquid), distinguishing them by suffixes 1, 2, 3 respectively and denoting the surface-tension coefficients at the interfaces by α12, α13, α23 (Fig. 77).
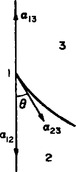
FIG. 77
Three surface-tension forces act on the line where all three bodies meet, each force being in the interface between the corresponding pair of bodies. We denote by θ the angle between the surface of the liquid and the plane surface of the solid, called the angle of contact. The value of this angle is determined by the condition of mechanical equilibrium: the resultant of the three surface-tension forces must have no component along the surface of the solid. Thus α13 = α12+α23 cos θ, whence
If α13 > α12, i.e. the surface tension between the gas and the solid is greater than that between the solid and the liquid, than cos θ > 0 and the angle of contact is acute, as in FIG. 77. If α13 < α12, however, the angle of contact is obtuse.
From the expression (161.1) we see that in any actual case of stable contact the inequality
must necessarily hold, since otherwise the condition of equilibrium would lead to an imaginary value of the angle θ, which has no meaning. On the other hand, if α12, α13, α23 are regarded as the values of the corresponding coefficients for each pair of bodies by themselves, without the third one, then it may well happen that the condition (161.2) is not satisfied. Actually, however, it must be remembered that when three different substances are in contact there may in general be an adsorbed film of each substance on the interface between the other two, and this lowers the surface tension. The resulting coefficients α will certainly satisfy the inequality (161.2), and such adsorption will necessarily occur if the inequality would not be satisfied without it.
If the liquid completely wets the solid surface, then a macroscopically thick liquid film, not an adsorbed film, is formed on the surface. The gas will therefore be everywhere in contact with the same liquid substance, and the surface tension between the solid and the gas is not involved at all. The condition of mechanical equilibrium gives simply cos θ = 1, i.e. the angle of contact is zero.
Similar arguments are valid for contact between three bodies of which none is solid: a liquid drop (3 in FIG. 78) on the surface of another liquid (1) adjoining a gas (2). In this case the angles of contact θ1 and θ2 are determined by the vanishing of the resultant of the three surface-tension forces, i.e. of their vector sum:
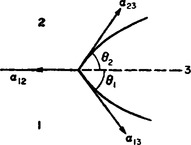
FIG. 78
Here it is evident that none of the quantities α12, α13, α23 can be greater than the sum or less than the difference of the other two.
§ 162 Nucleation in phase transitions
If a substance is in a metastable state, it will sooner or later enter another state which is stable. For example, supercooled vapour in time condenses to a liquid; a superheated liquid is converted into vapour. This change occurs in the following manner. Owing to fluctuations, small quantities of a new phase are formed in an originally homogeneous phase; for example, droplets of liquid form in a vapour. If the vapour is the stable phase, these droplets are always unstable and eventually disappear. If the vapour is supercooled, however, then when the droplets formed in it are sufficiently large they are stable and in time begin to grow and form a kind of centre of condensation for the vapour. The droplets must be sufficiently large in order to compensate the unfavourable energy change when a liquid-vapour interface is formed.†
Thus there is a certain minimum or critical size necessary for a nucleus, as it is called, of a new phase formed in a metastable phase, in order for it to become a centre for formation of the new phase. Since one phase or the other is stable for sizes less than and greater than the critical, the “critical nucleus” is in unstable equilibrium with the metastable phase. In what follows we shall discuss the probability that such nuclei occur.‡ The onset of the phase transition is governed by the probability that nuclei of just this minimum necessary size occur. See further Physical Kinetics, § 99.
Let us consider the formation of nuclei in isotropic phases: the formation of liquid droplets in supercooled vapour, or of vapour bubbles in superheated liquid. A nucleus may be regarded as spherical, since, owing to its very small size, the effect of gravity on its shape is entirely negligible. For a nucleus in equilibrium with the surrounding medium we have, from (156.2), P′—P = 2α/r, and the radius of the nucleus is therefore
the primed and unprimed letters everywhere refer to the nucleus and to the main (metastable) phase respectively.
According to the general formula (112.1), the probability w of a fluctuation producing a nucleus is proportional to exp (–Rmin/T), where Rmin is the minimum work needed to form the nucleus. Since the temperature and chemical potential of the nucleus have the same values as in the surrounding medium (the main phase), this work is given by the change in the potential Ω in the process. Before the formation of the nucleus, the volume of the metastable phase was V + V′ and its potential Ω = —P(V + V′); after the formation of the nucleus of volume V′, the potential Ω of the whole system is —PV – P′V′ +α. We therefore have
For a spherical nucleus V′ — 4πr3/3 and = 4πr2, and replacing r by (162.1) we find
As in § 156, we denote by P0 the pressure of both phases (at a given temperature T) when the interface between them is plane; in other words, P0 is the pressure for which the given value of T is the ordinary phase transition point, from which the superheating or supercooling is measured. If the metastable phase is only slightly superheated or supercooled, the differences ΔP = P—P0, ΔP′ = P′—P0 are relatively small and satisfy the equation (156.4):
where v′ and v are the molecular volumes of the nucleus and the metastable phase. Replacing P′—P by ΔP′—ΔP in (162.3) and expressing ΔP′ in terms of ΔP from (162.4), we find for the probability of formation of a nucleus in a slightly superheated or supercooled phase
In the formation of vapour bubbles in a superheated liquid we can neglect v in this formula in comparison with v′:
In the formation of liquid droplets in a supercooled vapour we can neglect v′ in (162.5) in comparison with v, and substitute v = T/P ≅ T/P0. This gives
The degree of metastability can be defined by the difference ΔT = T—T0 between the temperature T of the metastable phase (with which the nucleus is in equilibrium) and the temperature T0 of equilibrium of the two phases when the interface is plane, instead of by ΔP. According to the Clapeyron-Clausius formula, ΔT and ΔP are related by
where q is the molecular heat of the transition from the metastable phase to the nucleus phase. Substituting ΔP in (162.5), we obtain for the probability of formation of a nucleus
If saturated vapour is in contact with a solid surface (the wall of a vessel) which is completely wetted by the liquid, condensation of the vapour will occur without nucleation, directly on this surface. The formation of a liquid film on the solid surface in this case does not require work to be done to form the interface, and so the existence of a metastable phase (supercooling of the vapour) is impossible.
For the same reason, superheating of a solid with a free surface is in general impossible. This is because usually liquids completely wet the surface of a solid phase of the same substance; consequently, the formation of a liquid layer on the surface of a melting body does not require work to be done to form a new surface.
The formation of nuclei within a crystal on melting can, however, occur if the necessary conditions of heating are maintained: the body must be heated internally and its surface kept at a temperature below the melting point. The probability of formation of nuclei then depends on elastic deformations accompanying the creation of liquid droplets within the solid.
PROBLEMS
PROBLEM 1
Determine the probability of formation of a nucleus of a liquid on a solid surface for a given (non-zero) value of the angle of contact θ.
SOLUTION
The nucleus will have the shape of a segment of a sphere with base radius r sin θ, r being the radius of the sphere. Its volume is V =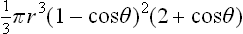 
, and the surface areas of the curved part and the base are respectively 2πr2(1-cos θ) and πr2 sin2 θ. Using the relation (161.1) for the angle of contact, we find that the change in ωs on formation of the nucleus is
where γ is the surface-tension coefficient between the liquid and the vapour. This change in ωs is the same as would occur in the formation, in the vapour, of a spherical nucleus of volume V and surface tension
Accordingly, the required formulae for the formation of nuclei are obtained from those derived in the text on replacing α by αeff.
SOLUTION
We regard the metastable phase as an external medium containing the nucleus, and calculate the work of formation of the nucleus from formula (20.2): Rmin = Δ(E—T0S+P0V) or, since in this case the process occurs at constant temperature equal to the temperature of the medium, Rmin = Δ(F+P0V). To determine this quantity, it is sufficient to consider only the amount of substance which enters the other phase (since the state of the remaining substance in the metastable phase remains unchanged). Again denoting the quantities pertaining to the substance in the original and the new phase by unprimed and primed letters respectively, we have
for a nucleus in unstable equilibrium with the metastable phase we should have Φ′(P′) = Φ(P) and thus return to (162.2).
Assuming the degree of metastability to be small, we have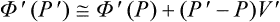 
, and (1) thus reduces to
where n = V′/v′ is the number of particles in the nucleus. For a spherical nucleus,
In the metastability range, μ(P) > μ′(P) and hence the first term (the volume term) is negative. The expression (2) may be said to describe the potential barrier which has to be overcome for the formation of a stable nucleus. It has a maximum at
corresponding to the critical radius of the nucleus. For r < rcr a decrease of r is energetically favourable and the nucleus is absorbed; for r > rcr an increase of r is favourable and the nucleus grows.†
§ 163 The impossibility of the existence of phases in one-dimensional systems
A problem of theoretical interest is that of the possibility of existence of more than one phase in one-dimensional (linear) systems, i.e. those in which the particles lie along a line. The following argument shows that in fact thermodynamic equilibrium between two homogeneous phases in contact at a single point and having arbitrarily large extent in length is not possible (L. D. Landau, 1950).
To prove this, let us imagine a linear system consisting of an alternation of sections formed by two different phases. Let Φ0 be the thermodynamic potential of this system, without allowance for the existence of points of contact between different phases, i.e. the thermodynamic potential of the total amounts of the two phases without regard to their division into sections. To take into account the effect of the points of contact, we note that the system may be formally regarded as a “solution” of these points in the two phases. If the “solution” is weak, the thermodynamic potential Φ of the system will be
where n is the number of points of contact in a length L. Hence
When the “concentration” n/L is sufficiently small (i.e. for a small number of sections of different phases), log(n/L) is large and negative, and therefore ∂Φ/∂n < 0. Thus Φ decreases with increasing n, and since Φ must tend to a minimum n will increase (until the derivative ∂Φ/∂n becomes positive). That is, the two phases will tend to intermingle in shorter and shorter sections, and therefore cannot exist as separate phases.
†In reality, of course, phases in contact are separated by a thin transition layer, but the structure of this is of no interest here, and we may regard it as a geometrical surface.
†The coefficient α is a function of only one independent variable; for such a function the partial derivatives with respect to μ and T have no meaning. But, by putting Ns = —(∂ωs/∂μ)T = 0, we have formally assumed that (∂α/∂μ)T = 0; in this case we clearly have dα/dT= (∂α/∂T)μ, and this has been used in (154.5).
†The use of the same letter for the surface tension and the critical index α is unlikely to cause any misunderstanding.
‡The width of the transition layer is equal to the correlation radius in the van der Waals theory also, and therefore the form ∝ (–t)2-α-v for the surface tension (without the use of (149.2)) would be valid in that theory. With α = 0, v = 1/2, the result would be (–t)3/2.
§This is discussed in more detail by L. D. Landau, Sbornik v chest’ 70-letiya A. F. Ioffe, p. 44, Moscow, 1950; translation in Collected Papers of L. D. Landau, p. 540, Pergamon, Oxford, 1965.
†The direction cosines of the radius vector are proportonal to p, q, — 1.
‡See the paper quoted in the first footnote to this section.
†The coefficient α is now a function of two independent variables, e.g. μ and T; the derivative ∂ωs/∂μ′ must be taken at constant T and chemical potential μ of the solvent. The condition Ns = —(∂ωs,/∂μ)μ′, T = 0 used here implies that we formally take (∂α/∂μ)μ′, T= 0 and therefore we can write equation (157.1) (cf. the second footnote to § 154).
†The expression for x2 in a solution differs from (78.8) only by a factor ε in the denominator.
‡For definiteness we shall consider adsorption from a gas phase.
§This rule is, however, not obeyed in practice for adsorption on a solid surface, since such a surface is never sufficiently homogeneous.
†Here we are considering adsorption on a liquid surface; adsorption on a solid surface is of no interest from this point of view, since, as mentioned above, such a surface is almost always inhomogeneous.
It may be noted that anisotropy of the interface between two isotropic phases (liquid and vapour) of the same pure substance is also possible in principle.
†The liquid itself is regarded as incompressible, i.e. we neglect the dependence of its chemical potential on the pressure.
†It should be borne in mind that this mechanism of formation of a new phase can actually occur only in a sufficiently pure substance. In practice, the centres of formation of the new phase are usually various kinds of “impurity” (dust particles, ions, etc.).
‡The calculation of the probability that nuclei of any size occur is given in Problem 2, and illustrates the relationships described.
†The calculation of Rmin for r = rcr naturally leads to formula (162.5) if we note that under these conditions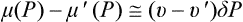 
. The formulae derived for the probability have no meaning if r > rcr. If a nucleus of this size is to occur, the liquid must be in a completely unstable state.