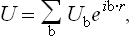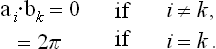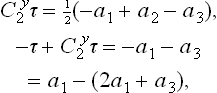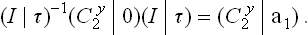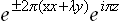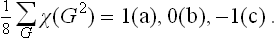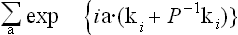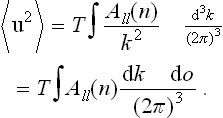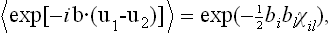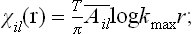THE SYMMETRY OF CRYSTALS
Publisher Summary
This chapter discusses the symmetry of crystals. The properties of symmetry of macroscopic bodies relate to the symmetry of the configuration of particles in them. Atoms and molecules in motion do not occupy precisely defined places in a body. For an exact statistical description of their arrangement, a density function is used that gives the probability of various configurations of the particles. The symmetry properties of the configuration of the particles are determined by the coordinate transformations, which leave the density function invariant. The set of symmetry transformations for a given body forms its symmetry group. If the body consists of different kinds of atom, the function must be determined for each kind of atom separately. The highest symmetry is that of isotropic bodies, which include gases, liquids, and amorphous solids. In such a body, all positions in space of any given particle must be equally probable. Besides translational symmetry, the lattice also has symmetry under certain rotations and reflections. The lattice points that can be made to coincide by any symmetry transformation are said to be equivalent.
§ 128 Symmetry elements of a crystal lattice
THE most usual properties of symmetry of macroscopic bodies relate to the symmetry of the configuration of particles in them.
Atoms and molecules in motion do not occupy precisely defined places in a body, and for an exact statistical description of their arrangement we must use a density function 
(x, y, z), which gives the probability of various configurations of the particles: dV is the probability that an individual particle is in the volume element dV. The symmetry properties of the configuration of the particles are determined by the coordinate transformations (translations, rotations and reflections) which leave the function (x, y, z) invariant. The set of all such symmetry transformations for a given body forms what is called its symmetry group.
If the body consists of different kinds of atom, the function must be determined for each kind of atom separately; this, however, is unimportant here, since all these functions in an actual body will in practice possess the same symmetry. We could also use the function defined as the total electron density due to all the atoms at each point in the body.†
The highest symmetry is that of isotropic bodies (bodies whose properties are the same in all directions), which include gases, liquids and amorphous solids. It is evident that in such a body all positions in space of any given particle must be equally probable, i.e. we must have = constant.
In anisotropic crystalline solids, on the other hand, the density function is not simply a constant. In this case it is a triply periodic function (with periods equal to those of the crystal lattice) and has sharp maxima at the lattice points. Besides translational symmetry, the lattice (i.e. the function (x, y, z)) also has, in general, symmetry under certain rotations and reflections. The lattice points which can be made to coincide by any symmetry transformation are said to be equivalent.
Proceeding to study the symmetry of a crystal lattice, we must first of all ascertain which elements can contribute to this symmetry.
The symmetry of a crystal lattice is based on its spatial periodicity, the property of being unchanged by a parallel displacement or translation through certain distances in certain directions;† translational symmetry will be further discussed in § 129.
As well as translational symmetry, the lattice may also be symmetrical under certain rotations and reflections; the corresponding symmetry elements (axes of symmetry, planes of symmetry, and rotary-reflection axes) are the same as those which can occur in symmetrical bodies of finite size (see Quantum Mechanics, § 91).
In addition, however, crystal lattices can also possess symmetry elements consisting of combinations of parallel translations with rotations and reflections. Let us first consider combinations of translations with the axes of symmetry. The combination of an axis of symmetry with a translation in a direction perpendicular to the axis does not give a new type of symmetry element. It is easy to see that a rotation through a certain angle followed by a translation perpendicular to the axis is equivalent to a rotation through the same angle about an axis parallel to the first. The combination of a rotation about an axis and a translation along that axis leads to a new type of symmetry element, a screw axis. The lattice has a screw axis of order n if it is unchanged by rotation through an angle 2π/n about the axis, accompanied by translation through a certain distance d along the axis.
After n rotations, with accompanying translations, about a screw axis of order n, the lattice is simply shifted along the axis by a distance nd. Thus, when there is a screw axis, the lattice must certainly also have a simple periodicity along this axis with a period not exceeding nd. This means that screw axes of order n can be correlated only with translations through distances d = pa/n (p = 1, 2, …, n − 1), where a is the smallest period of the lattice in the direction of the axis. For example, a screw axis of order 2 can be of only one type, the translation being through half a period; screw axes of order 3 can be correlated with translations by 
or 
period, and so on.
Similarly, we can combine translations with planes of symmetry. Reflection in a plane together with translation in a direction perpendicular to the plane does not give a new type of symmetry element, since such a transformation is easily seen to be equivalent to a reflection in a plane parallel to the first. The combination of a reflection with a translation along a direction lying in the reflection plane leads to a new type of symmetry element, a glide-reflection plane or glide plane. The lattice has a glide-reflection plane if it is unchanged by a reflection in this plane, accompanied by a translation through a certain distance d in a certain direction lying in this plane.
A twofold reflection in a glide-reflection plane amounts to a translation through a distance 2d. It is therefore clear that a lattice can have only glide-reflection planes such that the translation distance 
, where a is the smallest period of the lattice in the direction of the translation.
The combination of rotary-reflection axes with translations does not lead to new types of symmetry element, since in this case any translation can be resolved into two parts, one perpendicular to the axis and the other parallel to it and therefore perpendicular to the reflection plane. Thus a rotary-reflection transformation followed by a translation is always equivalent to another rotary-reflection transformation about an axis parallel to the first.
§ 129 The Bravais lattice
The translational periods of a lattice can be represented by vectors a whose directions are those of the respective translations and whose magnitudes are equal to the distances concerned. The lattice has an infinity of different lattice vectors. These vectors are not all independent, however: one can always choose three basic lattice vectors (corresponding to the three dimensions of space) which do not lie in one plane, and then any other lattice vector can be represented as a sum of three vectors each an integral multiple of one of the basic vectors. If the basic vectors are denoted by a1, a2, a3, an arbitrary lattice vector a will be of the form
where n1, n2, n3 are any positive or negative integers or zero.
The choice of the basic lattice vectors is not unique. On the contrary, they may be chosen in an infinity of ways. Let a1, a2, a3 be basic lattice vectors, and let us replace them by other vectors a′1, a′2, a′3, defined by the formulae
where the αik are some integers. If the new periods a′i are also basic lattice vectors, then, in particular, the vectors ai must be expressible in terms of the a′i as linear functions with integral coefficients; then any other lattice vector can also be expressed in terms of the a′i. In other words, if we express the ai in terms of the a′i in accordance with (129.2), the resulting formulae must be of the type
with the βik again integral. The determinant |βik| is the reciprocal of the determinant |αik|, and since both are integers it follows that the equation
is a necessary and sufficient condition for the a′i to be basic lattice vectors.
Let us choose a lattice point and mark off from it three basic lattice vectors. The parallelepiped formed by the three vectors is called a unit cell of the lattice. The whole lattice can then be regarded as a regular assembly of such parallelepipeds. All the unit cells are, of course, identical in their properties; they have the same shape and size, and each contains the same number of atoms of each kind identically arranged.
It is evident that identical atoms will be found at every vertex of every unit cell. All these vertices, therefore, are equivalent lattice points, and each can be brought to the position of any other by translation through a lattice vector. A set of all such equivalent points which can be brought into coincidence by a translation forms what is called a Bravais lattice of the crystal. This clearly does not include every point of the crystal lattice; indeed, in general it does not even include all equivalent points, since the lattice may contain equivalent points which can be made to coincide only by transformations involving rotations or reflections.
The Bravais lattice can be constructed by selecting any crystal lattice point and performing all possible translations. By taking initially some other point not in the first Bravais lattice we should obtain another Bravais lattice displaced relative to the first. It is therefore clear that the crystal lattice in general consists of several interpenetrating Bravais lattices, each corresponding to atoms of a particular type and position. All these lattices, regarded as sets of points (i.e. purely geometrically), are completely identical.
Let us return now to the unit cells. Because the choice of the basic lattice vectors is arbitrary, that of the unit cell is also not unique. The unit cell can be constructed from any basic vectors. The resulting cells are, of course, of varying shapes, but their volumes are all equal. This is most simply seen as follows. It is clear from the above discussion that each unit cell contains one point belonging to each of the Bravais lattices that can be constructed in the crystal concerned. Consequently, the number of unit cells in a given volume is always equal to the number of atoms of a particular type and position, i.e. is independent of the choice of cell. The volume of each cell is therefore the same, and equal to the total volume divided by the number of cells.
§ 130 Crystal systems
Let us now consider the possible types of symmetry of the Bravais lattices.
First, we shall prove a general theorem concerning the symmetry of crystal lattices with respect to rotations. Let us see which axes of symmetry the lattice can have. Let A (Fig. 55) be a point of a Bravais lattice, lying on an axis of symmetry perpendicular to the plane of the diagram. If B is another point separated from A by one of the possible translations, a similar axis of symmetry must pass through B.
FIG. 55
Let us now perform a rotation through an angle (ϕ = 2π/n about the axis through A, where n is the order of the axis. Then the point B and the axis through it will move to B′. Similarly, a rotation about B carries A into A′. From their construction, the points A′ and B′ belong to the same Bravais lattice, and so can be made to coincide by a translation. The distance A′B′ must therefore also be a translational period of the lattice. If a is the shortest period in the direction concerned, the distance A′B′ must therefore be equal to pa with p integral. It is seen from the figure that this gives
or cos 
.
Since | cos ϕ | 
1, p can be 3, 2, 1 or 0. These values correspond to ϕ = 2π/n with n = 2, 3, 4 or 6. Thus the crystal lattice can have axes of symmetry only of order 2, 3, 4 and 6.
Let us now examine the possible types of symmetry of the Bravais lattice under rotations and reflections. These types of symmetry are called crystal systems, and each corresponds to a certain set of axes and planes of symmetry, i.e. is a point group.
It is easy to see that every point of a Bravais lattice is a centre of symmetry thereof. For to each atom in a Bravais lattice there corresponds another atom collinear with that atom and with the lattice point considered, and such that the two atoms are equidistant from this lattice point. If the centre of symmetry is the only symmetry element of the Bravais lattice (apart from translations), we have
1. The triclinic system. This system, the least symmetrical of all, corresponds to the point group Ci The points of a triclinic Bravais lattice lie at the vertices of equal parallelepipeds with edges of arbitrary lengths and arbitrary angles between edges. Such a parallelepiped is shown in Fig. 56. The Bravais lattices are customarily denoted by special symbols; that of the triclinic system is denoted by Γt.
FIG. 56
2. The monoclinic system is next in degree of symmetry. Its symmetry elements are a second-order axis and a plane of symmetry perpendicular to this axis, forming the point group C2h. This is the symmetry of a right parallelepiped with a base of any shape. The Bravais lattice for this system can be constructed in two ways. In one, called the simple monoclinic Bravais lattice (Γm), the lattice points are at the vertices of right parallelepipeds with the ac face an arbitrary parallelogram (Fig. 56). In the other, the base-centred lattice 
, the lattice points are not only at the vertices but also at the centres of opposite rectangular faces of the parallelepipeds.
3. The orthorhombic system corresponds to the point group D2h. This is the symmetry of a rectangular parallelepiped with edges of any length. The system has four types of Bravais lattice. In the simple orthorhombic lattice (Γo), the lattice points are at the vertices of rectangular parallelepipeds. In the base-centred lattice 
, there are in addition lattice points at the centres of two opposite faces of each parallelepiped. In the body-centred lattice 
, the points are at the vertices and centres of the parallelepipeds; finally, in the face-centred lattice 
, the points are at the vertices and at the centre of each face.
4. The tetragonal system represents the point group D4h; this is the symmetry of a right square prism. The Bravais lattice for this system can be constructed in two ways, giving the simple and body-centred tetragonal Bravais lattices (Γq and 
), whose points lie respectively at the vertices and at the vertices and centres of right square prisms.
5. The rhombohedral or trigonal system corresponds to the point group D3d: this is the symmetry of a rhombohedron (a solid formed from a cube by stretching or compressing it along a spatial diagonal). In the only Bravais lattice possible in this system (Γrh) the lattice points are at the vertices of rhombohedra.
6. The hexagonal system corresponds to the point group D6h; this is the symmetry of a regular hexagonal prism. The Bravais lattice for this system (Γh) can be constructed in only one way; its lattice points are at the vertices of regular hexagonal prisms and at the centres of their hexagonal bases. It is useful to mention the following difference between the rhombohedral and hexagonal Bravais lattices. In both, the lattice points lie in planes perpendicular to the axis of order 3 or 6, and form a network of equilateral triangles; but in the hexagonal lattice the points are directly superimposed in successive such planes (in the direction of the C6 axis); these planes are shown in plan in Fig. 57. In the rhombohedral lattice, on the other hand, the points in each plane lie above the centres of the triangles formed by the points in the previous plane, as shown by the circles and crosses in Fig. 57.
FIG. 57
7. The cubic system corresponds to the point group Oh; this is the symmetry of a cube. This system has three types of Bravais lattice: the simple cubic (Γc), the body-centred cubic 
and the face-centred cubic 
.
In the sequence of systems: triclinic, monoclinic, orthorhombic, tetragonal, cubic, each has higher symmetry than those which precede it, i.e. each contains all the symmetry elements which appear in the preceding ones. The rhombohedral system is similarly of higher symmetry than the monoclinic, while at the same time it is of lower symmetry than the cubic and hexagonal systems: its symmetry elements are present in both of the latter, which are the two systems of highest symmetry.
We may also mention the following fact. It might appear at first sight that further types of Bravais lattice beyond the fourteen listed above are possible. For instance, if we add to the simple tetragonal lattice a point at the centre of each opposite square base of the prisms, the lattice would again be of tetragonal symmetry. However, it is easy to see that this would not give a new Bravais lattice. For, on joining the points of such a lattice in the manner indicated in Fig. 58 by the broken lines, we see that the new lattice is again a simple tetragonal one. The same is easily found to be true in all similar cases.
FIG. 58
The Bravais lattice parallelepipeds shown in Fig. 56 themselves have all the symmetry elements of the system to which they belong. However, it must be remembered that, for all the Bravais lattices except the simple ones, these parallelepipeds are not unit cells: the lattice vectors from which they are constructed are not basic ones. As the basic lattice vectors in the face-centred Bravais lattices we can take the vectors from any vertex of the parallelepiped to the centres of the faces, in the body-centred lattices from a vertex to the centres of the parallelepipeds, and so on. Fig. 59 shows the unit cells for the cubic lattices 
and 
; these cells are rhombohedra and do not themselves possess all the symmetry elements of the cubic system. It is evident that the volume vf of the face-centred Bravais parallelepiped is four times that of the unit cell: vf = 4v. The volumes of the body-centred and base-centred parallelepipeds are twice that of the unit cell: vv = 2v; vb = 2v.
FIG. 59
In order to define completely the triclinic Bravais lattice, it is necessary to specify six quantities: the lengths of the edges of its parallelepipeds and the angles between the edges. In the monoclinic system four quantities are sufficient, since two of the angles between the edges are always right angles. Similarly, we easily find that the Bravais lattices of the various systems are defined by the following numbers of quantities (lengths of edges of parallelepipeds or angles between edges): triclinic 6, monoclinic 4, orthorhombic 3, tetragonal 2, rhombohedral 2, hexagonal 2, cubic 1.
§ 131 Crystal classes
In many effects which may be called macroscopic, a crystal behaves as a homogeneous and continuous body. The macroscopic properties of the crystal depend only on the direction considered in it. For example, the properties of the passage of light through a crystal depend only on the direction of the light ray; the thermal expansion of a crystal is in general different in different directions; finally, the elastic deformations of a crystal under various external forces also depend on direction.
On the other hand, the symmetry of crystals brings about an equivalence of various directions in them. All macroscopic properties of a crystal will be exactly the same in such directions. We can therefore say that the macroscopic properties of the crystal are determined by the symmetry of directions in it. For instance, if the crystal has a centre of symmetry, every direction in it will be equivalent to the opposite direction.
Translational symmetry of the lattice does not lead to equivalence of directions, since parallel displacements do not affect directions. For the same reason, the difference between screw axes and simple axes of symmetry, and between simple planes of symmetry and glide-reflection planes, does not affect the symmetry of directions.
Thus the symmetry of directions, and therefore that of the macroscopic properties of the crystal, are determined by its axes and planes of symmetry, with screw axes and glide planes regarded as ordinary axes and planes. Such sets of symmetry elements are called crystal classes.
As we already know, an actual crystal may be regarded as a set of several interpenetrating identical Bravais lattices. Because of this superposition of the Bravais lattices, the symmetry of an actual crystal is in general different from that of the corresponding Bravais lattice.
In particular, the set of symmetry elements forming the class of a given crystal is in general different from its system. It is evident that the addition of further points to a Bravais lattice can only eliminate some of its axes or planes of symmetry, not introduce new ones. Thus the crystal class contains fewer (or at most the same number of) symmetry elements than the corresponding system, i.e. the set of axes and planes of symmetry of the Bravais lattice of the crystal in question.
From this we can derive a method of finding all the classes belonging to a given system. To do so, we must find all the point groups which contain some or all of the symmetry elements of the system. It may happen, however, that a point group thus obtained comprises symmetry elements present in more than one system. For example, we have seen in § 130 that all Bravais lattices have a centre of symmetry. The point group Ci is therefore present in all systems. Nevertheless, the distribution of crystal classes among systems is usually physically unique: each class must be assigned to the system of lowest symmetry among those which contain it. For example, the class Ci must be assigned to the triclinic system, which has no symmetry element except a centre of inversion. With this method of assigning the classes, a crystal having a certain Bravais lattice will never be placed in a class which could be constructed from a Bravais lattice of a system of lower symmetry–with one exception (see below).
The necessity of satisfying this condition is physically evident: it is physically most improbable that the atoms in a crystal which belong to its Bravais lattice should be arranged more symmetrically than is required by the symmetry of the crystal. Moreover, even if such a configuration were to occur by chance, any external perturbation, even a weak one (heating, for example), would be sufficient to destroy this configuration, since it is not imposed by the symmetry of the crystal. For instance, if a cubic Bravais lattice were to occur in a crystal belonging to a class for which the tetragonal system was sufficient, even a slight interaction would be capable of lengthening or shortening one of the edges of the cubic cell, converting it into a right square prism.
From this example we see the importance of the fact that the Bravais lattice of a system of higher symmetry can be converted to that of a system of lower symmetry by means of an arbitrarily small deformation. There is one exceptional case, however, where such a transformation is not possible: a hexagonal Bravais lattice cannot be converted by any infinitesimal deformation into the lattice of the rhombohedral system, which is of lower symmetry. For we see from Fig. 57 that, to transform the hexagonal into the rhombohedral lattice, it is necessary to move the lattice points in alternate layers by a finite amount from the vertices to the centres of the triangles. In consequence, all the classes of the rhombohedral system can be obtained with either a hexagonal or a rhombohedral Bravais lattice.†
Thus, to find all the crystal classes, we must first look for the point groups of the triclinic system, which has the lowest symmetry, and then go on in turn to systems of higher symmetry, omitting those of their point groups (i.e. classes) which have already been assigned to systems of lower symmetry. It is found that there are altogether 32 classes; a list of these arranged according to systems is as follows:
In each of these sets of classes the last is the one of highest symmetry, and contains all the symmetry elements of the corresponding system. The classes whose symmetry is equal to that of the system are called holohedral classes. Those whose number of different symmetry transformations (rotations and reflections, including the identical transformation), is less than for a holohedral class by a factor of two or four are called hemihedral and tetartohedral classes respectively. For example, in the cubic system the class Oh is holohedral, O, Th and Td are hemihedral, and T is tetartohedral.
§ 132 Space groups
Having studied the symmetry of the Bravais lattices and the symmetry of directions in the crystal, we can, finally, go on to consider the complete actual symmetry of crystal lattices. This symmetry may be termed microscopic, in contradistinction to the macroscopic symmetry of crystals discussed in § 131. The microscopic symmetry determines those properties of a crystal which depend on the arrangement of the atoms in its lattice (e.g. the scattering of X-rays by the crystal).
The set of (actual) symmetry elements of the crystal lattice is called its space group. The lattice always has a certain translational symmetry, and may also have simple, rotary-reflection and screw axes of symmetry and simple and glide-reflection planes of symmetry. The translational symmetry of the lattice is entirely determined by its Bravais lattice, since by the definition of the latter the crystal lattice can have no translational periods except those of its Bravais lattice. Hence, to determine the space group of a crystal, it is sufficient to find the Bravais lattice and to enumerate the symmetry elements which involve rotations and reflections, including of course the relative position of these axes and planes of symmetry. It must also be remembered that the translational symmetry of the crystal lattice means that, if the lattice possesses an axis or plane of symmetry, there exists an infinity of parallel axes or planes which are carried into one another by displacements through the lattice vectors. Finally, in addition to these axes (or planes) of symmetry separated by lattice vectors, the simultaneous presence of translational symmetry and the axes (or planes) of symmetry results in the existence of other axes (or planes) which cannot be made to coincide with the former by a translation through any lattice vector. For example, the presence of a plane of symmetry involves not only planes parallel to it at distances equal to the lattice vector but also planes of symmetry which bisect each lattice vector: it is easily seen that reflection in any plane followed by translation through a distance d in a direction perpendicular to the plane is equivalent to reflection in a plane parallel to the first and at a distance 
from it.
The possible space groups can be divided among the crystal classes, each space group being assigned to the class where the set of axes and planes of symmetry is the same as in the space group when no distinction is made in the latter between simple and screw axes and between simple and glide planes. Altogether 230 different space groups† are possible; they were first found by E. S. Fedorov (1895). The space groups are distributed among classes as shown in Table 1.
Table 1
We shall not pause here to enumerate the symmetry elements of all the space groups, which would be a very lengthy process. They may be found in manuals of crystallography.†
The space groups that contain no screw axes and glide planes are said to be symmorphic; there are 73 of these. The remaining 157 space groups contain such symmetry elements. The crystal lattices that belong to non-symmorphic space groups must certainly contain at least two identical atoms in each unit cell: since a rotation about a screw axis or a reflection in a glide plane involves a translation through a fraction of a basic lattice vector, the Bravais lattice points are not carried into one another by such transformations, and the crystal lattice must therefore consist of at least two interpenetrating Bravais lattices occupied by identical atoms.
§ 133 The reciprocal lattice
All physical quantities which describe the properties of a crystal lattice have the same periodicity as the lattice itself. Such quantities are, for example, the charge density due to the electrons in the atoms in the lattice, the probability of finding an atom at a particular point in the lattice, and so on.
Let the function U(r) be any such quantity. Its periodicity implies that
for any integral n1, n2, n3 (a1, a2, a3 being the basic vectors of the lattice).
Let us expand the periodic function U(r) as a triple Fourier series, which may be written
where the summation is over all possible values of the vector b. These are determined from the requirement that the function U, when put in the form of the series (133.2), satisfies the periodicity condition (133.1). This means that the exponential factors must be left unchanged when r is replaced by r +a, a being any lattice vector. For this to be so it is necessary that the scalar product a·b should always be an integral multiple of 2π. Taking a successively as the basic vectors a1, a2, a3, we must therefore have a1·b = 2πp1, a2·b = 2πp2, a3·b = 2πp3, where p1, p2, p3 are positive or negative integers or zero. The solution of these three equations has the form
where the vectors bi are given in terms of the ai by
We have thus determined the possible values of the vector b. The summation in (133.2) is taken over all integral values of p1, p2, p3.
Geometrically, the product v = a1·a2×a3 represents the volume of the parallelepiped formed by the vectors a1, a2, a3, i.e. the volume of the unit cell; the products a1×a2, etc., represent the areas of the three faces of this cell. The vectors bi therefore have the dimensions of reciprocal length, and in magnitude are equal to 2π times the reciprocal altitudes of the parallelepiped formed by the vectors a1, a2, a3.
From (133.4) it is seen that bi and ai are related by
Hence the vector b1 is perpendicular to a2 and a3, and similarly for b2 and b3.
Having defined the vectors bi, we can formally construct a lattice with b1, b2, b3 as basic vectors. This is called the reciprocal lattice, and the vectors b1, b2, b3 are called the (basic) vectors of the reciprocal lattice.†
Let us calculate the volume of the unit cell of the reciprocal lattice. This is v′ = b1·b2×b3. Substitution of the expressions (133.4) gives
It is evident that the reciprocal lattice cell corresponding to a triclinic Bravais lattice will also be an arbitrary parallelepiped. Similarly, the reciprocal lattices of the simple Bravais lattices of the other systems are also simple lattices of the same system; for example, the reciprocal lattice of a simple cubic Bravais lattice also has a simple cubic cell. It is also easy to see by a straightforward construction that the reciprocal lattices of the face-centred Bravais lattices (orthorhombic, tetragonal and cubic) are body-centred lattices of the corresponding systems; the volume of the Bravais parallelepiped in the reciprocal lattice is v′v = (2π)3 8/vf, where vf is the volume of the Bravais parallelepiped in the original lattice. Conversely, the body-centred original lattices correspond to face-centred reciprocal lattices, again with v′f = (2π3)8/vv. Lastly, base-centred lattices have reciprocal lattices which are also base-centred, with v′b = (2π)3 4/vb.
An equation of the form b·r = constant, where b is a given vector, represents a plane perpendicular to the vector b and at a distance from the origin equal to the constant divided by b. Let us take the origin at any of the Bravais lattice points, and let b = p1b1 + p2b2 + p3b3 be any vector of the reciprocal lattice (p1, p2, p3 being integers). Also writing r in the form a = n1a1 + n2a2 + n3a3, we obtain the equation of a plane:
where m is a given constant. If this equation represents a plane containing an infinity of Bravais lattice points (called a crystal plane), it must be satisfied by a set of integers n1, n2, n3. For this to be so, the constant m must clearly be an integer also. For given p1, p2, p3, when the constant m takes various integral values, equation (133.7) successively defines an infinity of crystal planes which are all parallel. A particular family of parallel crystal planes thus defined corresponds to each reciprocal lattice vector.
The numbers p1, p2, p3 in (133.7) can always be taken as mutually prime, i.e. as having no common divisor except unity. If there were such a divisor, both sides of the equation could be divided by it, leaving an equation of the same form. The numbers p1, p2, p3 are called the Miller indices of the family of crystal planes in question and are written as (p1p2p3).
The plane (133.7) intersects the coordinate axes (taken along the basic lattice vectors a1, a2, a3) at the points ma1/p1, ma2/p2, ma3/p3. The ratio of the intercepts (measured in units of a1, a2, a3 respectively) is 1/p1: 1/p2: 1/p3, i.e. they are in inverse proportion to the Miller indices. For instance, the Miller indices of planes parallel to the coordinate planes (i.e. having intercepts in the ratio ∞: ∞: 1) are (100), (010), (001) for the three coordinate planes respectively. Planes parallel to the diagonal plane of the basic parallelepiped of the lattice have indices (111), and so on.
It is easy to find the distance between two successive planes of the same family. The distance of the plane (133.7) from the origin is 2πm/b, where b is the length of the reciprocal lattice vector concerned. The distance of the next plane from the origin is 2π(m + 1)/b, and the distance d between these two planes is
The following formula is useful in applications:
where the summations on the left and right are taken over all vectors of the reciprocal and original lattices respectively. The sum on the right is a function of r that is periodic in the original lattice, and the left-hand side expresses it as a Fourier series.† The corresponding formula
follows immediately from (133.9), because of the symmetrical relationship between the two lattices.
§ 134 Irreducible representations of space groups
The physical applications of the theory of symmetry generally involve using the mathematical formalism of what are called representations of groups. In this section we shall discuss the question of the classification and method of constructing the irreducible representations of the space groups.‡
Let us first summarise in more mathematical terms the information given in the preceding sections about the structure of space groups.
Each space group contains a sub-group of translations comprising an infinity of all possible parallel displacements which leave the crystal lattice unchanged; this sub-group is the mathematical expression of the Bravais lattice of the crystal. The complete space group is obtained from this sub-group by adding n symmetry elements involving rotations and reflections, where n is the number of symmetry transformations of the corresponding crystal class; we shall call these the rotational elements. Every element of the space group may be represented as the product of one of the translations and one of the rotational elements.§
If the space group does not contain screw axes and glide planes (a symmorphic group), the rotational elements can be taken simply as the n symmetry transformations (rotations and reflections) of the crystal class. In non-symmorphic groups, the rotational elements are rotations and reflections combined with a simultaneous translation through a certain fraction of one of the basic vectors of the lattice. In such space groups, the rotational elements of symmetry are “interlinked” with translations and do not themselves form a sub-group; for example, a repeated reflection in a glide plane is not an identical transformation but a translation through one of the basic vectors of the lattice.
In order to characterise explicitly the elements of the space group, it is convenient to denote them by symbols (P|t), where P is any rotation or reflection and t the vector of a simultaneous translation; the effect of this element on the radius vector r of any point is shown by (P| t)r = Pr +t. The multiplication of elements follows the obvious rule
The element inverse to (P | t) is
on multiplication by (P | t) it gives the unit element (E | 0) of the group, wher e E denotes the identical rotation.
In particular, the pure translations are represented by the symbol (E | a), where a is any of the lattice vectors. The rotational elements in symmorphic groups, chosen as described above, are of the form (P | 0). In non-symmorphic groups, the rotational elements have the form (P | τ), where τ is the fraction of a lattice vector through which translation takes place along the screw axis or glide plane. In the former case, the set of rotational transformations (P | 0) is itself a sub-group of the space group. In the latter case, the elements (P | τ) themselves do not form a sub-group, since a repeated application of them gives not the identical transformation but a translation through one of the basic lattice vectors. The rotations and reflections P as such (i.e. if the differences between simple and screw axes, and between simple and glide planes, are ignored) always form a group, however, namely the point symmetry group which defines the crystal class; this point group may conveniently be called in this respect the direction group of the lattice.†
Let us now construct the irreducible representations of the space groups.‡
Any such representation can be given by a set of functions of the form
where the k are constant wave vectors, the ukα are functions invariant under translations, and the suffix α = 1, 2, … labels functions with the same k.
As a result of a parallel displacement r → r +a (where a is any vector of the lattice), the functions (134.3) are multiplied by constants eik·a. In other words, the matrices of translations are diagonal in the representation given by the functions (134.3). It is evident that two vectors k which differ by b (where b is any vector of the reciprocal lattice) will give the same law of transformation of the functions ϕkα by translations: since a·b is an integer times 2π, eia·b = 1. Such vectors k will be said to be equivalent. If we imagine the vectors k drawn from a vertex of a reciprocal lattice cell to various points, the non-equivalent vectors will correspond to the points in one unit cell.
By the application of a rotational element of symmetry (P | τ), the function ϕkα is transformed into a linear combination of the functions ϕk′α with various values of α and a vector k′ which is obtained from k by means of the rotation or reflection in question, performed in the reciprocal lattice: k′ = Pk.† The set of all (non-equivalent) vectors k which can be obtained from one another by the application of all n rotational elements of the group is called the star of the wave vector k. In the general case of arbitrary k the star contains n vectors (rays). The functions ϕkα which form the basis of an irreducible representation must always include functions having all the different rays of the star of k: since functions with non-equivalent k are multiplied by different factors under translations, no choice of linear combinations of them can bring about a decrease in the number of functions which are transformed into combinations of one another.
For certain values of k the number of rays in its star may be less than n, since it may happen that some of the rotational elements of symmetry leave k unchanged or transform it into an equivalent vector. For example, if the vector k is along an axis of symmetry, it is unchanged by rotations about this axis; a vector k from a vertex to the centre of the unit cell, i.e. 
, where bi is one of the basic vectors of the reciprocal lattice, is transformed by inversion into the equivalent vector 
.
The set of rotational elements of symmetry (regarded as all being simple rotations or reflections P) which appear in a given space group and which do not alter the vector k (or which transform it into an equivalent vector) is called the proper symmetry group of the vector k, or simply the group of k; it is one of the ordinary point symmetry groups.
Let us first consider the simple case of symmorphic space groups. The base functions of an irreducible representation of such a group can be written as products
where the uα are invariant under translations and the ψk are linear combinations of the expressions eik·r (with equivalent k) invariant with respect to the transformations in the proper symmetry group of the vector k; in (134.4) this vector takes all the values in its star. In translations the functions uα are unchanged, but the functions ψk, and therefore the ϕkα, are multiplied by eik·a. In rotations and reflections belonging to the group of k, the functions ψk are unchanged but the functions uα are transformed into combinations of one another. Thus the functions uα give one of the irreducible representations of the point group, these being called in this connection small representations. Finally, rotational elements which are not in the group of k transform sets of functions (134.4) with non-equivalent k into combinations of one another. The dimension of the representation of the space group thus constructed is equal to the number of rays in the star of k multiplied by the dimension of the small representation.
Thus the problem of finding all irreducible representations of symmorphic space groups reduces entirely to the classification of the vectors k with respect to their proper symmetry and the known problem of discovering the irreducible representations of finite point groups.
Let us now consider space groups which have screw axes or glide planes. The presence of such elements of symmetry is still unimportant if the wave vector k is such that it remains unchanged (i.e. is not transformed into an equivalent vector) under all the transformations in its group.† In this case the corresponding irreducible representations are again given by functions of the form (134.4), in which the uα form the basis of a representation of the point group of the vector k. The only difference from the previous case will be that under rotational transformations the functions ψk = eik·r in (134.4) will not remain unchanged, but will be multiplied by eik·r.
Functions of the form (134.4) become inapplicable, however, if there are several equivalent vectors k transformed into one another by transformations in their proper symmetry group. In a rotational transformation with a simultaneous translation τ, functions eik·r with equivalent but different values of k are multiplied by different factors (since b·τ/2π is not integral), and therefore their linear combinations ψk will not be transformed into combinations of one another.
In such cases it is no longer possible to consider the rotational elements and the translations separately, but of the infinity of translations it is sufficient to consider a finite number only. These cases arise for vectors k from a vertex of a unit cell of the reciprocal lattice to various special points within the cell, all or some of whose coordinates are simple rational fractions of the basic vectors b1, b2, b3.† We shall call the extended group of the wave vector the group consisting of the rotational elements (together with the relevant translations through fractions of a period τ) and those translations for which k·a/2π is a rational fraction (< 1); the remaining translations are again regarded as identical transformations. The functions ϕkα which give irreducible representations of the finite group thus formed (small representations), together with the corresponding functions ϕk′α for other rays in the star of k, give an irreducible representation of the space group. The dimension of the small representations in these groups may be as high as six (for the crystal class Oh).‡
This procedure will now be demonstrated for a specific example.
Let us consider the space group 
which corresponds to the simple orthorhombic Bravais lattice and contains the following rotational elements:§
the x, y and z axes being taken along the three basic vectors of the lattice; 
; the axes of symmetry C2 are simple axes but the planes σ perpendicular to them are glide planes.
Let us take, for example, the vector
the three numbers in parentheses give the components of the vector along the reciprocal lattice axes, measured in units of the edge lengths (bi = 2π/ai) of the reciprocal lattice cell. Its proper symmetry includes all the axes and planes of the point group D2h, and so this vector is its own star. The extended group is got by adding the translation (E | a1) for which 
. Thus we obtain a group of 16 elements in 10 classes as shown in the upper line in Table 2. The fact that the elements 
and 
, for example, are conjugate (i.e. belong to the same class) may be seen as follows. We have
Table 2
But
and, since translations through a3 and 2a1 must be regarded as identical transformations, we have
From the numbers of elements and classes in the group we find that it has eight one-dimensional and two two-dimensional irreducible representations (8·12+2·22 = 16). All the one-dimensional representations are obtained from representations of the point group D2h, the translation (E|a1) being assigned the character 1. These representations, however, occur here as “spurious” representations and must be rejected. They do not solve the problem in question: their base functions are invariant under all translations, whereas the functions eik·r with given k are certainly not invariant with respect to the translation (E | a1). Thus there remain only two irreducible representations, whose characters are shown in Table 2. The base functions of these representations can be taken as
the coordinates x, y, z are measured in units of the respective basic vectors a1, a2, a3.
Let us also consider the representations corresponding to the star of two vectors
with proper symmetry C2v (the axis C2 being along the z-axis); x is an arbitrary number between 0 and 1 (other than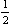 
). The extended group of k contains eight elements in five classes (Table 3). (The dependence of the base functions of the representations of this group on z reduces to a common factor e2πixz or e−-2πixz, which is invariant under all transformations of the group; it is therefore unnecessary to extend the group by translations along the z-axis.) There are four one-dimensional and one two-dimensional irreducible representation of this group. The one-dimensional representations must be rejected for the same reason as previously, leaving only one representation, whose characters are shown in Table 3. Its base functions can be taken as
Table 3
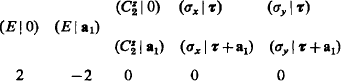
with the plus and minus signs in the exponent for the two vectors (134.6) respectively; the complete irreducible representation of the whole space group is four-dimensional, and is given by all four of these functions together.
§ 135 Symmetry under time reversal
In physical applications of the theory of symmetry groups, a further condition is usually imposed on their representations, namely that the base functions should be real (or rather reducible to a real form). This arises in consequence of the symmetry under time reversal. In quantum mechanics, this symmetry has the result that complex-conjugate wave functions must correspond to the same energy level of the quantum system, and must therefore appear among the base functions of the same physically irreducible representation (cf. Quantum Mechanics, § 96). In classical theory, however, this symmetry is expressed by the invariance of the equations of motion under the change t → – t; the equation contains time derivatives of an even order, the second. Consequently, the equations for the displacements us of the atoms in the lattice remain real when their solution is sought in the complex form (69.6) (∝ e−iωt); the amplitudes of these expressions can therefore be taken to be real.†
Real base functions, of course, remain real under the action of any element of symmetry; thus all the group representation matrices are real. If, however, any irreducible representation does not satisfy the condition, it must be combined with the complex-conjugate representation to form one physically irreducible representation of twice the dimension. Let us consider from this standpoint the cases that can occur for representations of space groups (C. Herring, 1937).
The simplest case in this respect is the one where the stars of the wave vectors k and – k do not coincide. Then the irreducible representations constructed from each star are certainly complex. For example, for the star of k the base functions of the representations are multiplied by factors eik·a under translations (E | a), and these factors include none that are complex conjugates; it is therefore clear that no choice of linear combinations of these functions can bring the matrices of the transformations to a real form. On the other hand, by taking the complex conjugates of these functions we obtain the complex-conjugate representation belonging to the star of the vector – k. By combining these two representations, we arrive at a real representation. Thus, to find a physically irreducible representation, we must include – k together with k in the star of each wave vector. That is, to obtain the whole of the required star we must apply to some original k all the elements of the direction group plus the centre of symmetry.
If, however, the star of the wave vector already contains all the necessary values of k, this does not guarantee that the irreducible representations constructed from them are real, as can be shown by a simple example.
Let us consider the symmorphic space group 
, belonging to the crystal class S4 and having a simple tetragonal Bravais lattice. In this group, we take the representations corresponding to the star of two vectors
where the z-axis is along the symmetry axis S4, and ℵ is an arbitrary number between 0 and 1 (other than 
). The proper symmetry of these vectors is C2, a point group having two one-dimensional representations with the following characters:
| E | C2 | |
| A | 1 | 1 |
| B | 1 | −1 |
Taking the first of these as the small representation, we get a two-dimensional representation of the whole space group, whose basis can be taken as the complex conjugate functions exp(±2πiℵz); this representation is therefore real. When B is the small representation, we have a two-dimensional representation of the whole group, with base functions
The characters of the rotational elements of the group in this representation are
and those of the translations are
| (E|a1) | (E|a2) | (E|a3) |
| 2 | 2 | 2 cos 2πx |
All these characters are real, but the representation is nevertheless complex: its base functions cannot be brought into a real form. The physically irreducible representation is found by adding to these functions their complex conjugates, and in this case therefore by combining two complex-conjugate but equivalent (with the same characters) representations.†
In the example considered, the symmetry under time reversal doubles the dimension of the physically irreducible representation for values of the wave vector on a straight line (the axis of symmetry) in k-space. There are also cases where this doubling occurs for values of k occupying a whole plane in k-space, this plane being perpendicular to a second-order screw axis.
Let us consider, for example, the non-symmorphic space group 
, which belongs to the crystal class C2 and has a simple monoclinic Bravais lattice. The second-order axis, which we take as the z-axis, is here a screw axis, with a translation through half a lattice vector: 
. In this group, we take the star of two wave vectors:
where ℵ and λ are arbitrary numbers between 0 and 
; the x- and y-axes are oblique, in a plane perpendicular to the axis of symmetry. The star includes k and –k, since the vectors (−ℵ, – λ, – 
) and (−ℵ, −λ, 
) are equivalent. This star corresponds to two equivalent (with the same real characters) two-dimensional irreducible representations of the group, given respectively by the base functions
and their complex conjugates. A physically irreducible representation is obtained by combining these two complex-conjugate representations. Its four base functions fall into two pairs each corresponding to one of the two wave vectors in the star:
If the irreducible representation is found together with its base functions, there is no difficulty in seeing whether it is real or complex. Nevertheless, in more complicated cases (and for the investigation of certain general problems) it is useful to have a criterion for answering this question from the characters of the small representation. Such a criterion can be obtained from the following general theorem in the theory of group representations.†
For each of the irreducible representations of the group, the following sum can have one of three values:
The summation is over all the elements in the group, and g is the order of the group. Correspondingly the representation is (a) real, (b) complex with non-equivalent complex-conjugate representations (they have complex-conjugate characters), (c) complex with equivalent complex-conjugate representations (they have equal real characters).
We shall outline the way in which this criterion can be converted for application to space groups, but not give the details. According to the method described in § 134 for the construction of irreducible representations of space groups, their characters may be expressed as
where ξk[(P | k)] are the characters of the rotational elements of the group in the small representation, and the summation is over those rays k1, k2, … of the star of the wave vector for which P is an element of the symmetry group. Applying this formula to the element
we have
with the substitution ki·Pa = a·P−-1ki in the exponent. These characters are to be summed over all translations and all rotational elements (P | τ). The sum
is zero except when ki + P−-1ki = 0 or b. Lastly, because all rays in the star are of equal significance, in the sum over i which is finally to be calculated all the terms are the same.
We thus obtain the Herring criterion:
where ξk are the characters of the small representation and the summation is over those rotational elements (P | τ) of the space group which convert k into a vector equivalent to – k: Pk = – k + b;† nk is the number of rotational elements in the proper symmetry of the wave vector.
In particular, if the space group contains no rotational elements having the specified property, the sum (135.5) has no terms, and case (b) occurs, in accordance with our previous discussion of the case where the stars of k and – k are not the same.
In the example of the group 
discussed above, the elements (S4 | 0) and 
have the desired property; their squares are the element (C2 | 0). The sum (135.5) is therefore
it is 1 for the small representation A and − 1 for the small representation B, for which we thus have cases (a) and (c), again in accordance with previous results.
§ 136 Symmetry properties of normal vibrations of a crystal lattice
One physical application of the mathematical theory of the representations of space groups is the classification of the normal vibrations of a lattice by means of their symmetry properties.†
It may be recalled that a lattice with v atoms in the unit cell has for any given wave vector k a total of 3v normal vibrations, each with its frequency ω(k). That is, over the whole range of variation of k the dispersion relation ω = ω(k) of the vibrations has 3v branches ωα(k); each of the ωα(k) takes values in a certain finite range, the phonon energy band. All the essentially different values of the wave vector lie in one unit cell of the reciprocal lattice; if we consider the whole infinite reciprocal lattice, the functions ωα(k) are periodic in it:
The physical principles of the classification of lattice vibrations by means of the irreducible representations of the symmetry group are the same as for the corresponding classification of finite symmetrical systems (polyatomic molecules: see Quantum Mechanics, § 100). The normal coordinates of the vibrations, which act as the basis of an irreducible representation of the symmetry group of the lattice, all belong to one frequency.
Each irreducible representation of the space group is specified, first of all, by its star of wave vectors. From this it follows immediately that the frequency is the same for all normal vibrations that differ only by values of k from the same star. Thus each function ωα(k) has the complete symmetry of directions for the crystal class concerned. As mentioned in § 135, the symmetry under time reversal means that the star of k must be supplemented by all vectors – k (if k and – k themselves do not coincide); thus we always have‡
For a given value of k (i.e. for one ray of the star), the normal coordinates are distributed among the bases of the small representations corresponding to various frequencies. If the dimension f of the small representation is more than one, there is degeneracy for the given value of k, the frequency in f branches being the same.
When the vector k has a general position in the reciprocal lattice, it has no proper symmetry (its group contains only the unit element, i.e. the identical transformation); all 3v values of ωα(k) are in general different. Degeneracy may occur if the proper symmetry of the wave vector is so high that its group has irreducible representations with dimension f > 1. With reference to the spatial symmetry only, this may take place either at isolated points in the lattice or on entire straight lines (axes of symmetry) in it. The symmetry under time reversal may also cause (twofold) degeneracy on entire planes in k-space (F. Hund, 1936; C. Herring, 1937). According to the discussion in § 135, this degeneracy can occur on planes perpendicular to a second-order screw axis; see the example of representations associated with the star (135.2).†
In order to classify the normal vibrations of a specific crystal lattice, we must first find the complete vibrational representation of the space group given by all the vibrational coordinates (atomic displacement vectors) together. This representation is reducible; by decomposing it into irreducible parts, we find the degree of degeneracy of the frequencies and the symmetry properties of the corresponding vibrations. It may happen that one representation appears several times in the vibrational representation: this means that there are several different frequencies with the same multiplicity corresponding to vibrations of the same symmetry.
This procedure is analogous to the method of classifying molecular vibrations (Quantum Mechanics, § 100). There is an important difference, however, in that the lattice vibrations are further characterised by the parameter k, which takes a continuous series of values, and the classification must be carried out for each value (or class of values) of the wave vector separately. If k is specified, the star of the irreducible representation of the space group is determined. It is therefore sufficient in practice to find the vibrational small representation and decompose it into irreducible small representations, i.e. irreducible representations of the symmetry group of the vector k.
The classification of the lattice vibrations in the limit as k → 0 is especially simple. When k = 0, the irreducible small representations for all the space groups (whether or not symmorphic) are the same as the irreducible representations of the point symmetry group of the lattice, namely its crystal class. To find the vibrational representation (Dvib) we must consider only the atoms in one unit cell, i.e. regard all translationally equivalent atoms† as one. Without repeating the whole discussion of the atomic vibrations in the molecule for this case, we can formulate the following rule for finding the characters of the vibrational representation of the lattice when k = 0. The characters of a rotation C(ϕ) through an angle ϕ about an axis of symmetry, or S(ϕ) about a rotary-reflection axis, are
where
are the characters of the representation given by the three components of a (polar) vector; vC and vS are the numbers of atoms which remain fixed or move to translationally equivalent places in the transformation.‡ The same formulae give the characters for reflection in a plane (transformation S(0)) and for inversion in a centre of symmetry (transformation S(π)). A rotation about a screw axis or a reflection in a glide plane certainly brings all the atoms into translationally non-equivalent positions, and for them we therefore always have ξ vib = 0.
These rules may be illustrated by an example.§ The diamond lattice belongs to the non-symmorphic space group 
. It has a face-centred cubic Bravais lattice with two like atoms in the unit cell at the vertices (000) and at the points 
on the spatial diagonals of the cubic cells.|| Half the rotational elements of the group 
coincide with rotations and reflections in the point group Td. These transformations leave both atoms fixed or move them to translationally equivalent positions. The characters of the vibrational representation for these elements are therefore ξvib = 2ξv. The remaining rotational elements of the group 
are screw rotations and reflections in glide planes, obtained by combining the elements of the group Td with inversion (I | τ), where 
; these elements move the atom at (000) to the translationally non-equivalent point 
, so that their characters are ξvib = 0. The decomposition of the resulting vibrational representation into irreducible representations of the point group Oh is Dvib = F2g + F2u.† The coordinates of the acoustic vibrations which describe the movement of the cell as a whole when k = 0 are transformed as the components of a vector, and therefore correspond to the representation F2u by which such components are transformed in the group Oh. The representation F2g corresponds to the triply degenerate limiting frequency of the optical vibrations.‡
The degeneracy of the optical vibrations is generally removed on leaving the point k = 0. According to the symmetry, the amount of splitting may vary near k = 0 as a homogeneous function of the first or second order in the components of the vector k. The appropriate criterion is easily ascertained in terms of quantum perturbation theory. The Hamiltonian of lattice vibrations with a small wave vector k ≡ δk has the form 
, where 
is the Hamiltonian of vibrations with k = 0, and 
is a vector operator; the term 
acts as the perturbation which causes the splitting. The amount of splitting is of the first order in δk if 
has non-zero matrix elements for transitions between states belonging to the same degenerate vibrational frequency; otherwise, the splitting is of the second order in δk. Here it must be noted that the operator 
changes sign under time reversal, since the wave vector δk changes sign while the product 
, like any Hamiltonian, must be invariant under time reversal. Thus the solution of the problem reduces to finding the selection rules for frequency-diagonal matrix elements of a vector operator that changes sign under time reversal (see Quantum Mechanics, § 97). If the degenerate frequency corresponds to an irreducible representation D, these rules depend on the decomposition of the antisymmetric part of its direct product with itself, {D2}; non-zero matrix elements exist if this expansion contains parts by which the components of a vector are transformed.
The splitting will certainly be of the second order in δk if the point symmetry group of the lattice (the crystal class) contains a centre of inversion; this is evident, since the squared basis of the representation {D2} must be even under inversion, whereas the components of a vector change sign. If the crystal class does not contain an inversion, there are two possibilities. For example, in the crystal class O, the antisymmetric products for the two-dimensional irreducible representation E and the three-dimensional representations F1 and F2 are†
The components of a vector are transformed by F1; hence the splitting of the doubly degenerate frequency will be of the second order in δk, and that of the triply degenerate ones will be of the first order.
Let us now consider vibrations with non-zero wave vector. For symmorphic space groups, they are classified in the same way as in the case k = 0 described above. The irreducible small representations are here the same as the irreducible representations of the point symmetry group of the vector k, and to find the vibrational small representation we must again consider only the atoms in one unit cell.
The procedure may be demonstrated for the optical vibrations of the diamond lattice. The face-centred Bravais lattice of this structure corresponds to a body-centred cubic reciprocal lattice. At the point k = 0 (the vertex of the cubic cell) the proper symmetry of the wave vector is Oh, and there is (as shown above) one triply degenerate frequency of optical vibrations, corresponding to the representation F2g; the characters of this representation are‡
Let us now see how this frequency is split when we leave the point k = 0.
A displacement along the spatial diagonal of the cubic cell gives the vector k the proper symmetry C3v. For this group the representation given by the same three vibrational coordinates is reducible:
| E | 2C3 | 3σ′ |
| 3 | 0 | 1 = E + A1 |
i.e. the triply degenerate frequency splits into one doubly degenerate and one non-degenerate frequency. A similar splitting occurs in a displacement along an edge of the cubic cell, where the proper symmetry of the wave vector is C4v:
In a displacement along a diagonal of a face of the cubic cell, the proper symmetry of the vector k is lowered to C2v, and the frequency splitting is complete:
For crystal lattices of non-symmorphic space groups, the procedure for classifying the normal vibrations is more laborious, and we shall not pause to discuss it here.†
§ 137 Structures periodic in one and two dimensions
A characteristic feature of solid crystals is that the density function (x, y, z) is periodic in three dimensions and extends to unlimited distances. Let us consider the possibility of the existence in Nature of bodies whose density functions are periodic in only one or two dimensions (R. E. Peierls, 1934; L. D. Landau, 1937).
For example, a body with = (x) could be regarded as consisting of parallel planes regularly arranged and lying perpendicular to the x-axis, with the atoms randomly distributed in each plane. When = (x, y), the atoms would be randomly distributed along lines parallel to the z-axis, but these lines themselves would be regularly arranged.
To discuss this question, let us consider the displacements undergone by small parts of the body as a result of thermal fluctuations. It is clear that, if such displacements increase without limit as the size of the body increases, there will necessarily be a “smoothing-out” of the function , in contradiction with hypothesis. In other words, only those structures can occur for which the mean displacement remains finite when the dimensions of the body become arbitrarily large.
Let us first confirm that this condition is satisfied in an ordinary crystal. Let u(x, y, z) denote the vector of the fluctuation displacement of a small region with coordinates x, y, z and let u be represented as a Fourier series:
the components of the vector k take both positive and negative values, and the coefficients uk are related by 
, since a is real. The series (137.1) will include only terms with not too large wave numbers,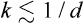 
, where d is the linear dimension of the region undergoing displacement. We shall consider the fluctuations at constant temperature; then their probability is given by
where
is the change in the total free energy of the body in the fluctuation, and F now denotes the free energy per unit volume of the body (cf. (116.7)).
To calculate ΔFt, we must expand 
in powers of the displacement. The expansion will involve not the function u(x, y, z) itself but only its derivatives, since 
must vanish when u = constant, corresponding to a simple displacement of the body as a whole. It is evident that the terms in the expansion which are linear in these derivatives must be absent, since otherwise F could not have a minimum for u = 0. Next, owing to the smallness of the wave numbers k, we need go only as far as the terms quadratic in the first derivatives of u in the expansion of the free energy, neglecting the terms containing the higher-order derivatives. Hence we find that ΔFt has the form
where the elements of the real tensor ϕil (i and l being the tensor indices, over which summation is implied) are quadratic functions of the components of the vector k.†
According to (111.9), we hence find for the mean square fluctuations of the Fourier components of the displacement vector
where 
are the components of the tensor inverse to ϕil.‡ For clarity, this expression may be written
where the Ail depend only on the direction of the vector k (n = k/k). The mean values 〈uiui〉 are found from (137.6) by summation over k; changing in the usual manner from this to integration, we get, for example, the mean square displacement vector
The integral converges at the lower limit (k → 0) linearly in k.† Thus the mean square of the fluctuation displacement is, as it should be, a finite quantity independent of the size of the body.
Next, let us consider a body with density function = (x). Since = constant along the y- and z-axes in such a body, no displacement along these axes can “smooth out” the density function, and such displacements are consequently of no interest here. We need therefore consider only a displacement ux. Moreover, it is easy to see that the first derivatives ∂ux/∂y, ∂ux/∂z cannot appear in the expansion of the free energy, since, if the body is rigidly rotated about the y- or z-axis, these derivatives change, whereas the free energy must obviously remain constant. Thus in the expansion of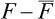 
we have to consider the following terms quadratic in the displacement:
the derivatives with respect to y and z appear symmetrically, owing to the complete symmetry in the yz-plane. Substitution in (137.3) leads to terms of the types
where 
. Although the two latter expressions include powers of the wave vector components higher than the first expression, they may be of the same order of magnitude, since nothing is known a priori concerning the relative magnitude of kx and ℵ.
Thus the change in the free energy will be of the form
where ϕ is a quadratic function of the variables kλ and ℵ2. Instead of (137.7), we now have
This integral is logarithmically divergent when k → 0. The divergence of the mean square displacement implies that a point to which a particular value of (x) corresponds may be displaced through very large distances; in other words, the density (x) is “smoothed out” through the whole body, so that no function (x) is possible except the trivial case = constant.
Similar arguments for a body with = (x, y) give the following expression for the mean squares of the displacement:
where ϕ is again a quadratic function of its arguments. This integral is easily seen to converge at the lower limit, so that the mean fluctuational displacement remains finite. Thus bodies having such a structure could in theory exist, but it is not known whether they do in fact exist in Nature.
So far in this section we have been concerned with three-dimensional bodies, and only the arrangement of the atoms was assumed to have a two-dimensional (or one-dimensional) ordering. Let us now consider the possibility of an ordered configuration of atoms in two-dimensional systems where the atoms occupy only a certain surface.† The two-dimensional analogue of ordinary solid crystals would be a film in which the atoms are regularly arranged at the points of a plane lattice. This configuration could be described by a density function (x, y) (which now has a different meaning from that used above, since only atoms on one surface z = constant are considered). It is easy to see, however, that the thermal fluctuations “smooth out” such a crystal, so that = constant is the only possibility: the mean values of the products of components of the fluctuational displacement u (in the xy-plane) are again determined by expressions of the form (137.6) and (137.7), except that the integration is now taken over two-dimensional k-space:
and the integral diverges logarithmically as k → 0.
Here, however, the following reservation is necessary. The result obtained, strictly speaking, means only that the fluctuational displacement becomes infinite when the size (area) of the two-dimensional system increases without limit (so that the wave number may be arbitrarily small). But, because of the slow (logarithmic) divergence of the integral, the size of the film for which the fluctuations are still small may be very great.† In such cases, a film of finite size might have practically “solid-crystal” properties and be approximately describable as a two-dimensional lattice. We shall see in § 138 that such properties of two-dimensional systems become more marked at lower temperatures.
§ 138 The correlation function in two-dimensional systems
The expression (137.11) gives the mean square fluctuational displacement at any specified point in a two-dimensional crystal system. A fuller understanding of the properties of such systems can be achieved by considering the correlation function between the fluctuations at different points in the system.
Let us note first of all that, when T = 0, a two-dimensional lattice of any size could exist: the divergence of the integral (137.11) is due to the thermal fluctuations (T ≠ 0). Let 0(r) be the density function of the system at T = 0.‡ We can determine the correlation function of the density fluctuations for non-zero but sufficiently low temperatures (much less than the Debye temperature). Under these conditions, only long-wavelength vibrations are excited in the lattice, i.e. the variation of the density function is determined mainly by the long-wavelength fluctuations.
Let the atoms at the points r in the lattice undergo fluctuational displacements u(r). If the function u(r) varies only slightly over distances of the order of a lattice constant (corresponding to the fluctuations with small wave numbers that we are concerned with here), the change in the density at each point in space may be regarded as simply the result of a shift of the lattice by an amount equal to the local value of the displacement vector. The fluctuating density is then written (r) = 0[r – u(r)], and the correlation between its fluctuations at different points r1 and r2 is determined by the mean value
The periodic function 0(r) can be expanded as a Fourier series (cf. (133.2)):
where the b are the vectors of the (plane) reciprocal lattice and the constant term 
has been separated from the sum. When these series are substituted in (138.1) and the result is averaged, the terms containing the products bb′ with b′ ≠ –b disappear, as will be shown below. The product with b′ = –b gives a contribution to (138.1)
for brevity, we write u(r1) = u1, u(r2) = u2.
The probability distribution for the fluctuations of the displacement vector is given by formula (137.2), in which ΔFt is a quadratic functional of u(r). If the values of u(r) for different (discrete) points in space are regarded as different fluctuating quantities ℵa (a = 1, 2, …), this means that the probability distribution for them is Gaussian. We can then use in the averaging in (138.3) the formula
(see § 111, Problem), obtaining
where
(r = r1 – r2). It remains to substitute u1 and u2 as the expansions (137.1). Noting that the mean values 〈uikulk〉 are zero when k′ ≠ – k, and are given by (137.11) when k′ = –k, we find
The integral converges for small k, since the factor 1 – cos k·r ∝ k2 when k → 0.† For large k, the integral diverges logarithmically. This divergence is actually due only to the fact that the approximations used are invalid for large k: when 
(where c is the velocity of sound; see § 110), the fluctuations cease to be classical. (At low temperatures this condition is violated sooner than k 
1/a, where a is the lattice constant.) Noting also that for large k the term containing the rapidly oscillating factor cos k·r in the integrand may be omitted, we find
the bar over Ail denotes averaging over the directions of the vector k in the plane.
The required correlation function is now obtained by substituting (138.6) in (138.3) and (138.4) and summing over b; the asymptotic law of decrease of this function with increasing distance r is given by the least rapidly decreasing term in the sum:
where b is to be taken as the reciprocal lattice basic vector for which αb has its least value.
Thus, in a two-dimensional lattice, the correlation function does tend to zero as r → ∞ (unlike a three-dimensional lattice, where it tends to a finite limit), but only according to a power law, and more slowly at low temperatures.† Note that the correlation function (138.7) depends on the direction of r, and the system therefore remains anisotropic.
Similar but slightly more laborious calculations give a law of the same type for the correlation function in a three-dimensional system with density function (x). For comparison, it may be recalled that in an ordinary liquid the correlation function decreases much more rapidly, in fact exponentially (see § 116).
§ 139 Symmetry with respect to orientation of molecules
The condition = constant is necessary but certainly not sufficient for a body to be isotropic. This is clear from the following example. Let us imagine a body consisting of elongated molecules, all positions in space of a molecule as a whole (i.e. of its centre of mass) being equally probable, but the axes of the molecules being predominantly oriented in one direction. Such a body is obviously anisotropic, despite the fact that = constant for each atom present in the molecule.
The property whose symmetry is here under consideration may be formulated in terms of a mutual correlation between the positions of the different atoms. Let 12 dV2 be the probability of finding an atom 2 in the volume element dV2 for a given position of atom 1 (atoms of different types usually being involved); 12 is a function of the coordinates r1 and r2 of the two atoms, and the symmetry properties of this function determine the symmetry of the body (in which = constant).
The fact that the density function is constant signifies that a relative displacement of parts of the body (without change of volume) does not affect the equilibrium state of the body, i.e. does not change its thermodynamic quantities. This is precisely the characteristic property of liquids (and gases). We must therefore regard bodies with = constant and an anisotropic correlation function 12 as forming a distinct category, liquid crystals (anisotropic fluids). These include bodies whose molecules are anisotropically distributed in respect of their spatial orientation.
Two types are possible as regards the symmetry of this distribution. For one type (nematic liquid crystals) the correlation function depends only on the difference r12 = r1 – r2; when the length of this vector varies without change in its direction, no periodicity of the correlation function occurs, though it may undergo oscillations which become less as r12 increases. The function thus has no translational symmetry, and its symmetry group must consist of various rotations and reflections, i.e. is a point group. Geometrically, it may be any point group, with symmetry axes of any order, but apparently all the known nematic liquid crystals have an axis of complete axial symmetry, and the two directions along this axis are equivalent. The point groups C∞h, D∞ and D∞h have these properties.† We shall see in § 140, however, that the symmetry D∞ (which has no plane of symmetry) makes the state of the liquid crystal unstable, and there consequently must appear a certain “secondary” periodic structure typical of liquid crystals of the other (cholesteric) type.
Besides these two types, there exist other anisotropic liquids with various layered structures, which are usually classed together as smectic liquid crystals. It seems that at least some of these have a density function (x) that is periodic in one direction only. Such substances may be regarded as consisting of freely moving plane layers at equal distances apart. In each layer the molecules have an ordered orientation, but the configuration of their centres of mass is random.
It has been shown in § 137 that structures with a one-dimensional periodicity of the density function are smoothed out by thermal fluctuations. The divergence of these fluctuations is, however, only logarithmic. Although this excludes the possibility of a one-dimensional periodicity extended to arbitrarily large distances, it does not exlude its existence over comparatively small but nevertheless macroscopic regions of space, as already noted at the end of § 137.
Finally, it may be mentioned that in ordinary isotropic liquids also there are two different types of symmetry. If the liquid consists of a substance which does not have stereoisomers, it is completely symmetrical not only under a rotation through any angle about any axis but also under a reflection in any plane, i.e. its symmetry group is the complete group of rotations about a point, together with a centre of symmetry (group Kh). If the substance has two stereoisomeric forms, however, and the liquid contains different numbers of molecules of the two isomers, it will not possess a centre of symmetry and therefore will not allow reflections in planes. Its symmetry group is just the complete group of rotations about a point (group K).
§ 140 Nematic and cholesteric liquid crystals
The orientational symmetry of nematic liquid crystals is uniaxial: at every point in the liquid there is only one preferred direction of orientation of the molecules, namely that of axial symmetry. The macroscopic state of such a body can therefore be described by specifying one unit vector n(r) at each point, having this preferred direction; it is called the director. In a complete equilibrium state the body is homogeneous, i.e. n = constant Inhomogeneous distributions n(r) describe various deformational states of the liquid crystal.
In a macroscopic deformation, n(r) varies slowly through the body; the characteristic dimensions of the deformation are large compared with molecular dimensions. The derivatives of n(r) with respect to the coordinates are therefore small quantities of an order that increases with that of the derivative. Representing the total free energy of the deformed liquid crystal (at a given temperature) as an integral Ft = ∫ F dV, we can expand the free energy density F in powers of the derivatives of n(r) (C. W. Oseen, 1933; F. C. Frank, 1958).
The expansion of the scalar quantity F can contain only scalar combinations of the components of the vector n and its derivatives. There are only two scalar combinations linear in the first derivatives: the true scalar div n and the pseudoscalar n·curl n. The former, on integration over the volume, becomes an integral over the surface of the body, and is therefore unimportant in considering the bulk properties of the substance.
True scalars quadratic in the first derivatives can be found by taking the rank-four tensor
and forming invariants from it by contraction with respect to pairs of suffixes or multiplication by components of the vector n. It must be noted here that n is a unit vector, so that
In this way we find the invariants
The last two, however, differ only by a divergence:
so that their contributions to the total free energy differ only by an integral over the surface of the body, which is of no interest here (J. L. Ericksen, 1962). The invariant†
and (n·curl n)2 may therefore be taken as the independent invariant. Lastly, there is a pseudoscalar quadratic in the first derivatives: (n·curl n) div n.‡
Scalars linear in the second derivatives are of the same order of smallness as the above, but integration by parts reduces all of them to forms quadratic in the first derivatives.
Thus we have the following expression for the free energy density of a liquid crystal:
where b, a1, a2, a3 and a12 are (temperature-dependent) constants.
As already mentioned in § 139, the directions of n and – n are equivalent in all known liquid crystals of these types; to meet this condition, we must put a12 = 0. Moreover, if the symmetry elements of the crystal include planes, b = 0: since n·curl n is a pseudoscalar and the free energy is a true scalar, the coefficient b must be a pseudoscalar; but a medium having planes of symmetry cannot have pseudoscalar characteristics, since reflection in the plane would give b = – b. Thus the free energy of a nematic liquid crystal is
All three coefficients a1, a2, a3 must be positive. Then n = constant corresponds to the equilibrium state.
If the liquid crystal does not have a plane of symmetry, then b ≠ 0.† We can rewrite (140.1) (with a12 = 0) as
where q0 = b/a2 (and the constant – b2/2a2 is included in F0). The equilibrium state of such a substance corresponds to a distribution of directions of the director such that
These equations have the solutions
This structure (corresponding to cholesteric liquid crystals) can be imagined as the result of a uniform twisting about the x-axis of a nematic medium originally oriented with n = constant in one direction in the yz-plane. The orientational symmetry of a cholesteric crystal is periodic in one direction (the x-axis) in space, so that the correlation function 12 = 12(x, r12). The vector n reverts to its original value after each interval of length 2π/q0 along the x-axis; but since the directions of n and – n are physically equivalent, the actual period of repetition of the structure is π/q0. A structure of this type is usually said to be helicoidal.
The above theory is, of course, valid only if the period of the helicoidal structure is large in comparison with molecular dimensions. This condition is in fact satisfied in cholesteric liquid crystals (the period π/q0 ˜ 10−-5 cm).
§ 141 Fluctuations in liquid crystals
Let us consider the fluctuations of the direction of the director n in a nematic liquid crystal (P. G. de Gennes, 1968).
We express n as n0 + v, where 
is the equilibrium direction, constant throughout the volume, and v ≡ Δn is the fluctuation from this value. Since 
, n0·v ≅ 0, i.e. the vector v is perpendicular to n0. Accordingly, the correlation function of the fluctuations,
is a two-dimensional tensor in the plane perpendicular to n0 (α and β being vector suffixes in that plane). In a homogeneous but anisotropic liquid, this function depends not only on the magnitude of the vector r = r2 – r1 but also on its direction.
A magnetic field has a strong influence on the fluctuations of the director. This is due to the presence, in the free energy density of a liquid crystal, of a further term
which depends on the vector n itself, not on its derivatives as in (140.2).† If ξa > 0, the equilibrium direction of n is the same as that of the field, but if ξa < 0 it is in the plane perpendicular to the field. We shall take the case where ξa > 0, so that n0|| H. Then (n·H)2 ≅ H2(1 – v2); omitting the term independent of v, we can write
Taking F from (140.2) and (141.3), and retaining only quantities of the second order in v, we get the following expression for the change in the total free energy in a fluctuation:
with the x-axis in the direction of no. It must be emphasised that, by using the expression (140.2) for the energy of the deformed crystal, we thereby limit the treatment to fluctuations with wavelengths much longer than molecular dimensions.
We now proceed as in § 116, expressing the fluctuating quantity v(r) as a Fourier series in the volume V:
After substitution of this series, the expression (141.4) forms a sum of terms (ΔFt)k, each of which depends only on the component vk with a particular value of k. Taking the xy-plane to contain the direction of k (and of H), we get
Hence (cf. § 116) we find for the mean square fluctuations
We see that, in the absence of the field, the fluctuations of the Fourier components vk increase without limit as k → 0 (the integrals over d3k, which give the mean square of the vector v itself, remain finite, however). The application of the magnetic field suppresses the fluctuations that have wave numbers 
(where a is the order of magnitude of the coefficients a1, a2, a3).†
The correlation function (141.1) can be calculated from (141.6), using the formula
cf. (116.13). We shall not pause to give the fairly lengthy formula resulting from the integration,‡ but only mention that, in the absence of the field, the correlation function decreases as 1/r with increasing distance r = |r2 – r1|. When the field is present, the decrease becomes exponential, with correlation radius rc ˜ (a/ξa)1/2 H−1.
The fluctuations of the direction of the director in a cholesteric liquid crystal can be treated similarly, and only a brief commentary will be given here.
In a cholesteric medium, we can distinguish the fluctuations of the local direction of the helicoidal structure axis and those of the phase (the angle of rotation of the vector n about this axis). Fluctuations of the first type are finite, but the mean square fluctuation of the phase is (in the absence of a magnetic field) logarithmically divergent as k → 0. In this respect, the fluctuations in a medium with one-dimensional periodicity of the orientational structure are analogous to those in a medium with one-dimensional periodicity of the particle configuration (§ 137). Strictly speaking, such periodicity is consequently impossible in a medium of arbitrarily great extent, but, on account of the large value of the helicoidal structure period in cholesteric liquid crystals, the divergence of the fluctuations would occur only for such huge dimensions that the whole question is a purely academic one.
We may add a few words about fluctuations in smectic liquid crystals consisting of regularly arranged plane layers. As already mentioned in § 139, such a structure is smoothed out by thermal fluctuations, and can therefore occur only in restricted volumes. It is interesting to note, however, that these fluctuations are suppressed by a magnetic field. The origin of this effect is as follows.
In each layer, the molecules are oriented in an ordered manner, with a preferred direction given by the director n; let this be normal to the surface of the layer. When fluctuations occur, the surface of the layers is deformed and the director is rotated. Let u be the displacement vector of points in a layer, and v again the change in the director (n = n0 + v). In long-wavelength deformations, the layer may be regarded as a geometrical surface, and the small quantities v and u are then related by v = – grad (u·n0) (the change of direction of the normal to the surface); for their Fourier components we have vk = – iℵ(uk·n0), where ℵ is the component of k in the plane of the layer. In the presence of the magnetic field, the change in direction of the director makes an additional contribution (141.3), proportional to v2, in ΔFt. This in turn has the result that the integral (137.9) which gives the mean square of the fluctuational displacement acquires a further term ˜ ℵ2 in the denominator of the integrand (together with a term in ℵ4), and in consequence the integral no longer diverges.
Lastly, let us consider fluctuations in two-dimensional liquid-crystal systems (films). In such a system, the orientation of the molecules is specified by a director n lying in the plane of the film. If we consider its fluctuations (with wave vectors k in the plane of the film), we get an expression analogous to (141.6): in the absence of a field, 
, where ϕ(kx, ky) is a quadratic function of the components of k. But to find the total fluctuation 〈v2〉 this expression must now be integrated over d2k ∝ k dk, and the integral diverges logarithmically. Thus the thermal fluctuations smooth out such a two-dimensional liquid-crystal structure. As with a two-dimensional solid crystal (§ 137), however, the logarithmic divergence does not exclude the existence of such a structure in regions of finite size.
†Moving electrons can cause not only a mean charge density e but also a mean current density j(x, y, z). Bodies in which there are non-zero currents are those having a “magnetic structure”, and the symmetry of the vector function j(x, y, z) determines the symmetry of that structure. This is discussed in Electrodynamics, § 28.
†Here the crystal lattice must be regarded as infinite, ignoring the faces of the crystal.
†Crystals of rhombohedral classes with a hexagonal Bravais lattice are usually assigned to the rhombohedral system.
†Including eleven pairs that are the same except for the direction of rotation about their screw axes.
†A full account of the space groups is given, for example, by G. Yu. Lyubarski, The Application of Group Theory in Physics, Pergamon, Oxford, 1960, and in the International Tables for X-Ray Crystallography, Vol. I, Kynoch Press, Birmingham, 1952. The latter also lists the equivalent points for each space group.
†The definition (133.4), which is now customary in the physics literature, differs by factors of 2π from that usual in pure crystallography.
†The divergence of the sum when r = a occurs because the lattice is infinite. In considering a lattice of large but finite volume, the sum when r = a is to be equated to the number of lattice cells N.
‡The reader is assumed familiar with group theory to the extent given, for example, in Quantum Mechanics, Chapter XII.
§The translation sub-group is Abelian (all its elements commute) and is a normal divisor of the complete space group: all elements of the group that are conjugate to translations are also translations. (Two elements A and B are said to be conjugate if A = C−-1BC with C a third element of the group.)
†In every case, the relation between the space group and the direction group may be formulated in the following way, using the group-theory standpoint. Let all the elements of the space group be distributed into n affine classes, each containing an infinity of products of one rotational element with all possible translations, i.e. all elements of the form (P | τ+a) with given P and τ. If we now regard the whole of each of these classes as an element in a new group, we get a factor group of the original space group, which is isomorphous with the direction group.
‡The arguments below are due to F. Seitz (1936).
†In transforming the vector k in the reciprocal lattice all axes and planes of symmetry must, of course, be treated as simple ones, i.e. only the direction group is to be considered.
†This always includes, in particular, the vector k = 0 and a vector in a general position in which the unit element of its group is the identical transformation.
†In practice these fractions are usually 
, 
or 
, the last two values occurring for groups of the rhombohedral and hexagonal systems.
‡If the representations of the extended group of the wave vector are regarded as representations of the unextended group (one of the point groups), then the relations between the matrices 
that represent the elements G of the group will be different from those between these elements themselves: if G1G2 = G3, the corresponding matrices of the representation will in general be related not by a similar equation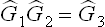 
(as in ordinary representations), but by 
, where ω12 is a phase factor equal to unity only in modulus: |ω12| = 1. Such representations are said to be projective. All the essentially different projective representations can be listed once and for all in each point group, and thereafter used as small representations for constructing irreducible representations of space groups.
An account of the theory of projective representations, and tables of them for the prystallographic point groups, will be found in G. L. Bir and G. E. Pikus, Symmetry and Deformation Effects in Semiconductors (Simmetriya i deformatsionnye éffekty v voluprovodnikakh), Nauka, Moscow, 1972.
There exist also complete tables of irreducible representations of space groups, which are given by O. V. Kovalev, Irreducible Representations of the Space Groups; Gordon & Breach, New York, 1965; C. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids, Clarendon Press, Oxford, 1972.
§The space groups are customarily denoted by the symbol for the crystal class, with an index which arbitrarily numbers the group within the class.
†This will not be so in the presence of a magnetic field or in a crystal having a magnetic structure.
†This kind of situation did not arise in point groups, for which all the irreducible representations with real characters are real.
†It is proved, for instance, in the books mentioned in the footnotes to §§ 132 and 134.
†Here (P | τ)2 does not alter the vector k (or converts it into an equivalent vector), and is therefore certainly part of the proper symmetry group of the vector k.
†Representations of space groups were first applied to the study of the physical properties of crystal lattices by F. Hund (1936) and by L. P. Bouckaert, R. Smoluchowski and E.P. Wigner (1936).
‡From the physical point of view, the relation between the transformation k → – k for the lattice vibrations and time reversal is obvious: a change in the sign of the time reverses the direction of wave propagation (or, in terms of the phonon picture, changes the sign of the phonon momentum p = 
k).
†Besides degeneracies due to the lattice symmetry, there can also be degeneracy for “accidental” values of k; the existence of such degeneracies could be theoretically predicted only by actually solving the equations of motion of the atoms in a specific lattice. For an analysis of possible cases, see C. Herring, Physical Review 52, 365, 1937 (reprinted in R.S. Knox and A. Gold, Symmetry in the Solid State, Benjamin, New York, 1964).
†These are the occupied sites in any one Bravais lattice.
‡For a molecule, a subtraction is needed in the characters of the vibrational representation in order to eliminate the coordinates that correspond to the displacement or rotation of the molecule as a whole. For a lattice, the number (six) of these degrees of freedom is negligible compared with the total number of degrees of freedom, and such a subtraction is not necessary.
§To avoid misunderstanding, we may note that the classification of the limiting frequencies of the optical branches of the vibrations by means of the crystallographic symmetry only of the lattice is not valid for ionic crystals. The long-wavelength optical vibrations of the ionic lattice are accompanied by the occurrence of macroscopic polarisation of the crystal and an associated macroscopic electric field, which in general modifies (and reduces) the symmetry of the vibrations.
||The coordinates of the atoms are specified with respect to the edges of the cubic cell and in units of the length of these edges. The volume of a face-centred cubic cell is four times that of the unit cell. The basic lattice vectors go from the vertex to the points 
, which are the centres of the faces of the cubic cell.
†The point group Oh may be regarded as the direct product O×Ci or Td×Ci; here we use the second form. Accordingly, the irreducible representations of the group Oh are constructed from representations of the group Td. In particular, the representations F2g and F2u of Oh are obtained from the representation F2 of Td, and differ in being respectively even and odd under inversion (see Quantum Mechanics, § 95).
‡The limiting frequency of the acoustic vibrations is always degenerate: the macroscopic nature of these vibrations leads to a single value ω = 0 for all three branches, even if this is not required by symmetry. In this sense the degeneracy is “accidental”.
†The notation for the irreducible representations of point groups is as in Quantum Mechanics, § 95.
‡The symmetry elements that appear in the point group Td are put first, followed by the elements obtained on multiplication of these by the inversion I. The elements 3C2 are rotations through a about axes along the edges of the cubic cell; 6C′2 are rotations through π about the diagonals of the faces; 6σ′ are reflections in planes through opposite edges; 3σ are reflections in the planes of the faces.
†Examples of such groups are given in the book by Bir and Pikus quoted in § 134.
†The terms containing products uikulk, exp [i(k + k′)·r] with k′ ≠ –k disappear on integration over the volume.
‡To determine the constant numerical coefficient in (137.5), we have to note that each product 
appears twice (for ±k) in (137.4), giving 2 re 
, and the real part of the product 
is itself the sum of two independent products.
†The integrand as written is valid only when k is not too large.
†Such are monomolecular adsorbed films at the interface between two isotropic phases; see § 159.
†The same applies to three-dimensional bodies with one-dimensional periodicity, for which the integral (137.9) diverges logarithmically.
‡Here and in the rest of § 138, r = (x, y) is the two-dimensional radius vector in the plane of the system.
†If we look into the origin of this factor, we see that it arises from the fact that b′ = –b in (138.3). It is easy to see that when b′ ≠ –b there will not be cancellation in the integrand and the integral will diverge. Since these integrals occur in the exponent (cf. (138.4)), their divergence means that the corresponding contributions to the correlation function are zero.
†A correlation function of this form was found by T. M. Rice (1965) for a two-dimensional superconductor, and by B. Jancovici (1967) and V. L. Berezinski
(1971) for a two-dimensional lattice.
†In the other groups with axial symmetry (C∞ and D∞v) the two directions along the axis are not equivalent. Such liquid crystals would in general be pyroelectric.
†This is easily proved by expressing in components and taking the z-axis in the direction of n at the relevant point in space (then ∂nz/∂xi = 0).
‡The product (n·grad)n·curl n = 0, since from grad n2 = 0 it follows that (n·grad)n = – n × curl n.
†This symmetry will always occur for a liquid crystal consisting of one stereoisomer of a substance that has molecules with mirror-type asymmetry (such as all the known cholesteric liquid crystals). Crystals consisting of two different stereoisomers of the same substance differ in the sign of the constant b.
†In a uniaxial anisotropic medium, the magnetic susceptibility is a tensor 
, and the magnetisation of the substance gives rise to a free energy term 
. The quantity (141.2) is the part of this contribution that depends on n.
†This type of fluctuation is analogous to the behaviour of the density fluctuations in an ordinary liquid near its critical point and that of the order parameter fluctuations near a phase transition point of the second kind (see § 146 and 152 below). Whereas in these latter cases the factor that suppresses the fluctuations is the “distance” from the points concerned, here it is the external magnetic field, which is independent of the temperature. Note that it is precisely the increase of the fluctuations of n when k is small that enables us to treat these fluctuations independently of those of other quantities. In this connection, it is important that we are not considering the neighbourhood of phase transition points of the second kind. Near such points, the fluctuations of other characteristics of the transition also increase, and the fluctuations of n cannot in general be dealt with independently of the others. It should also be emphasised that the increase of the fluctuations does not lead to any limitations on the range of applicability of (141.6), whereas the validity of formula (146.8), for example, is subject to the inequality (146.15).
‡In deriving this, the expressions (141.6) must, of course, be rewritten in a form that does not involve a particular choice of the coordinate axes.