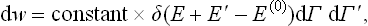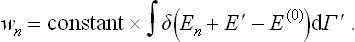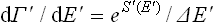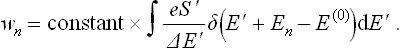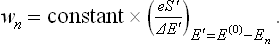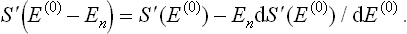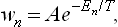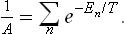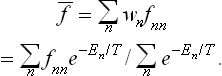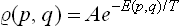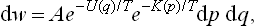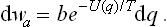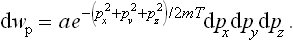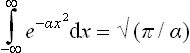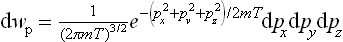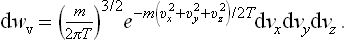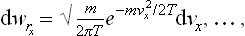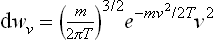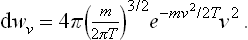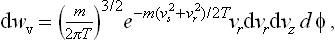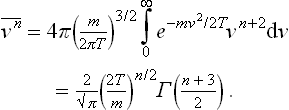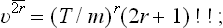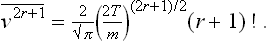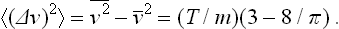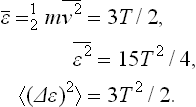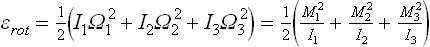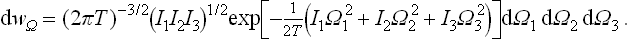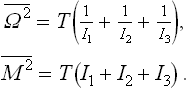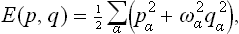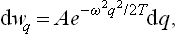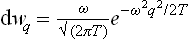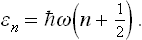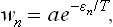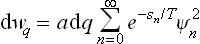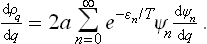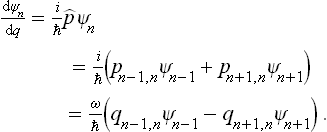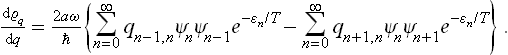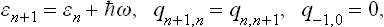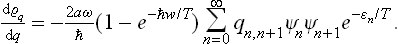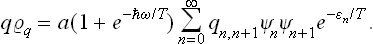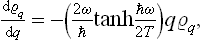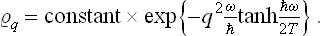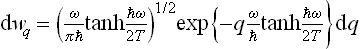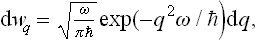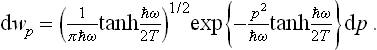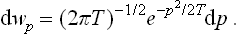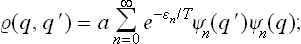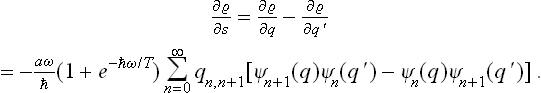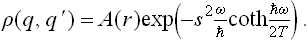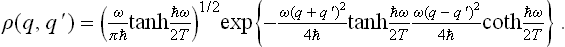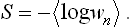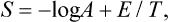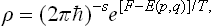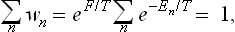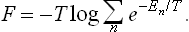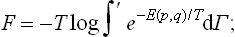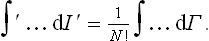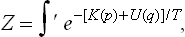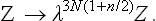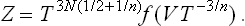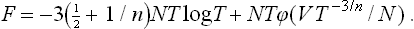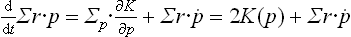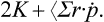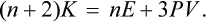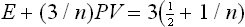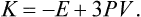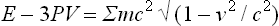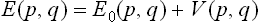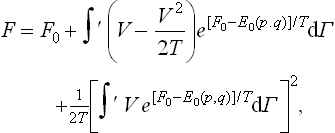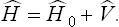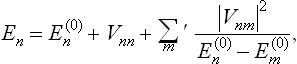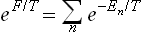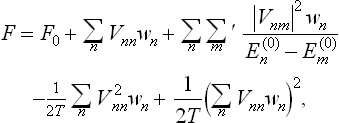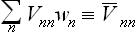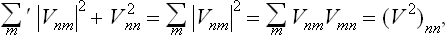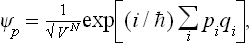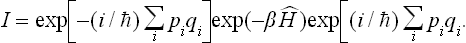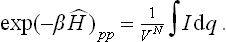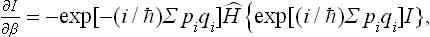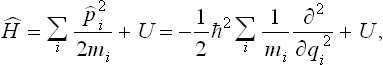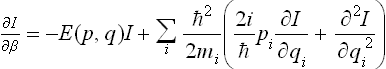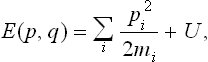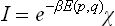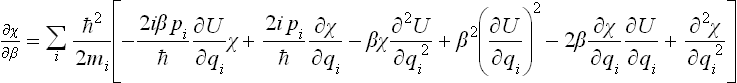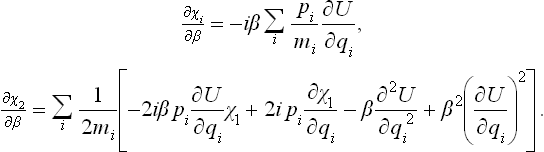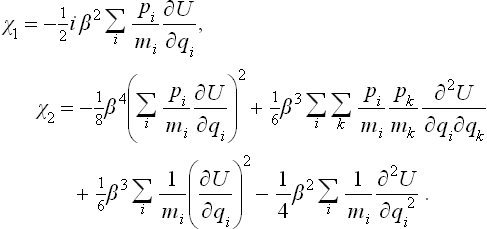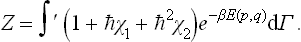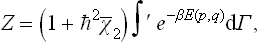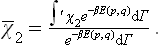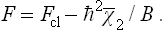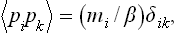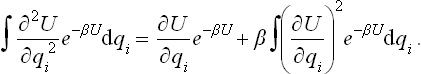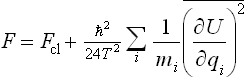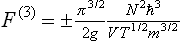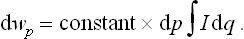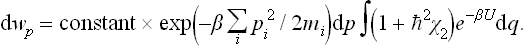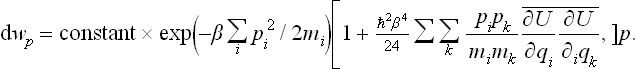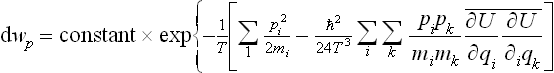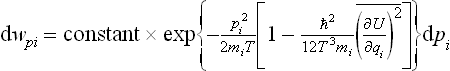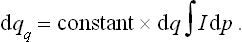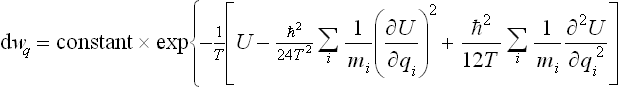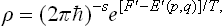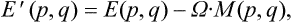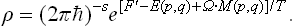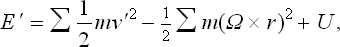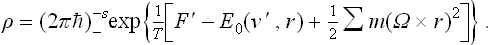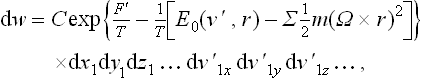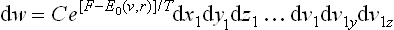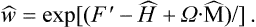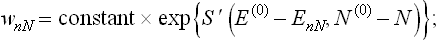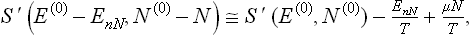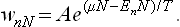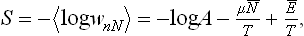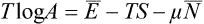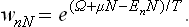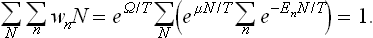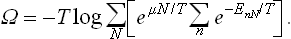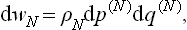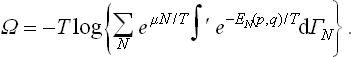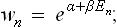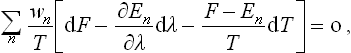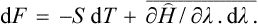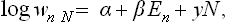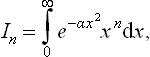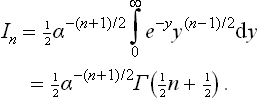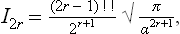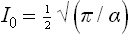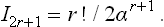THE GIBBS DISTRIBUTION

Publisher Summary

This chapter discusses the Gibbs distribution. The possibility of applying the Gibbs distribution to closed systems can be seen from the fact that this distribution hardly differs from the microcanonical distribution, while being convenient for practical calculations. The canonical distribution is spread over a certain range of energy values, but the width of this range is negligible for a macroscopic body. The energy in the Gibbs distribution formula of classical statistics can be written as the sum of two parts: the kinetic energy and the potential energy. The first of these is a quadratic function of the momenta of the atoms, and the second is a function of their coordinates, the form of which depends on the law of interaction between the particles within the body. The probabilities for momenta and coordinates are independent, in the sense that any particular values of the momenta do not influence the probabilities of the various values of the coordinates and vice versa.

LET us now turn to the problem stated in Chapter I of finding the distribution function for a subsystem, i.e. any macroscopic body which is a small part of some large closed system. The most convenient and general method of approaching the solution of this problem is based on the application of the microcanonical distribution to the whole system.

Distinguishing the body in question from the rest of the closed system, we may consider the system as consisting of these two parts. The rest of the system will be called the “medium” in relation to the body.

The microcanonical distribution (6.6) can be written in the form

(28.1)

where E, dΓ and E′, dΓ′ relate to the body and the medium respectively, and E⁽⁰⁾ is the given value of the energy of the closed system, which must be equal to the sum E+E′ of the energies of the body and the medium.

Our object is to find the probability w_n of a state of the whole system such that the body concerned is in some definite quantum state (with energy E_n), i.e. a microscopically defined state. The microscopic state of the medium is of no interest, so that we shall suppose this to be in a macroscopically defined state. Let δΓ′ be the statistical weight of the macroscopic state of the medium and let δE′ be the range of values of the energy of the medium corresponding to the range δΓ′ of quantum states in the sense discussed in § 7.

The required probability w_n can be found by taking dΓ = 1 in (28.1), putting E = E_n and integrating with respect to Γ′:

Let Γ′(E′) be the total number of quantum states of the medium with energy not exceeding E′. Since the integrand depends only on E′, we can change to integration with respect to E′, putting dΓ′ = (dΓ′(E′)/dE′)dE′. The derivative dΓ′/dE′ is replaced (cf. § 7) by

where S′(E′) is the entropy of the medium as a function of its energy; δE′ is, of course, also a function of E′. Thus we have

Owing to the presence of the delta function, the result of the integration is simply to replace E′ by E⁽⁰⁾–E_n:

(28.2)

We now use the fact that, since the body is small, its energy E_n is small in comparison with E⁽⁰⁾. The quantity ΔE′ undergoes only a very small relative change when E′ varies slightly, and so in ΔE′ we can simply put E′ = E⁽⁰⁾; it then becomes a constant independent of E_n. In the exponential factor e^S′, we must expand S′(E⁽⁰⁾ – E_n) in powers of E_n as far as the linear term:

The derivative of the entropy S′ with respect to energy is just 1/T, where T is the temperature of the system; the temperatures of the body and the medium are the same, since the system is assumed to be in equilibrium.

Thus we have finally for w_n the expression

(28.3)

where A is a normalisation constant independent of E_n. This is one of the most important formulae in statistical physics. It gives the statistical distribution of any macroscopic body which is a comparatively small part of a large closed system. The distribution (28.3) is called the Gibbs distribution or canonical distribution; it was discovered by J. W. Gibbs for classical statistics in 1901.

The normalisation constant A is given by the condition Σw_n = 1, whence

(28.4)

The mean value of any physical quantity f pertaining to the body can be calculated by means of the Gibbs distribution, using the formula

(28.5)

In classical statistics an expression exactly corresponding to (28.3) is obtained for the distribution function in phase space:

(28.6)

where E(p, q) is the energy of the body as a function of its coordinates and momenta.^† The normalisation constant A is given by the condition

(28.7)

In practice, cases are frequently encountered where it is not the entire microscopic motion of the particles which is quasi-classical, but only the motion corresponding to some of the degrees of freedom, whereas the motion with respect to the remaining degrees of freedom is quantised (for example, the translational motion of the molecules may be quasi-classical while the motion of the atoms within the molecules is quantised). Then the energy levels of the body may be written as functions of the quasi-classical coordinates and momenta: E_n = E_n(p, q), where n denotes the set of quantum numbers defining the “quantised part” of the motion, for which p and q are parameters. The Gibbs distribution formula then becomes

(28.8)

where d_p_cld_q_cl is the product of differentials of the “quasi-classical” coordinates and momenta.

Finally, the following comment is necessary concerning the group of problems which may be solved by means of the Gibbs distribution. We have spoken of the latter throughout as the statistical distribution for a subsystem, as in fact it is. It is very important to note, however, that this same distribution can quite succesfully be used also to determine the fundamental statistical properties of bodies forming closed systems, since such properties of a body as the values of the thermodynamic quantities or the probability distributions for the coordinates and velocities of its individual particles are clearly independent of whether we regard the body as a closed system or as being placed in an imaginary thermostat (§ 7). But in the latter case the body becomes a “subsystem” and the Gibbs distribution is immediately applicable to it. The difference between bodies forming closed and non-closed systems when the Gibbs distribution is used appears essentially only in the treatment of the fairly unimportant problem of fluctuations in the total energy of the body. The Gibbs distribution gives for the mean fluctuation of this quantity a non-zero value, which is meaningful for a body in a medium but is entirely spurious for a closed system, since the energy of such a body is by definition constant and does not fluctuate.

The possibility of applying the Gibbs distribution (in the manner described) to closed systems is also seen from the fact that this distribution hardly differs from the microcanonical distribution, while being very much more convenient for practical calculations. For the microcanonical distribution is, roughly speaking, equivalent to regarding as equally probable all microstates of the body which correspond to a given value of its energy. The canonical distribution is “spread” over a certain range of energy values, but the width of this range (of the order of the mean fluctuation of energy) is negligible for a macroscopic body.

§ 29 The Maxwellian distribution

The energy E(p, q) in the Gibbs distribution formula of classical statistics can always be written as the sum of two parts: the kinetic energy and the potential energy. The first of these is a quadratic function of the momenta of the atoms,^† and the second is a function of their coordinates, the form of which depends on the law of interaction between the particles within the body (and on the external field, if any). If the kinetic and potential energies are denoted by K(p) and U(q) respectively, then E(p, q) = K(p) + U(q), and the probability dw = (p, q) dp dq becomes

i.e. is the product of two factors, one of which depends only on the coordinates and the other only on the momenta. This means that the probabilities for momenta and coordinates are independent, in the sense that any particular values of the momenta do not influence the probabilities of the various values of the coordinates, and vice versa. Thus the probability of the various values of the momenta can be written

(29.1)

and the probability distribution for the coordinates is

(29.2)

Since the sum of the probabilities of all possible values of the momenta must be unity (and the same applies to the coordinates), each of the probabilities dw_p and dw_q must be normalised, i.e. their integrals over all possible values of the momenta and coordinates respectively for the body concerned must be equal to unity. From these conditions we can determine the constants a and b in (29.1) and (29.2).

Let us consider the probability distribution for the momenta, and once again emphasise the very important fact that in classical statistics this distribution does not depend on the nature of the interaction of particles within the system or on the nature of the external field, and so can be expressed in a form applicable to all bodies.^†

The kinetic energy of the whole body is equal to the sum of the kinetic energies of each of the atoms composing it, and the probability again falls into a product of factors, each depending on the momenta of only one atom. This again shows that the momentum probabilities of different atoms are independent, i.e. the momentum of one does not affect the probabilities of various momenta of any other. We can therefore write the probability distribution for the momenta of each atom separately.

For an atom of mass m the kinetic energy is 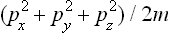, where p_x, p_y, p_z are the Cartesian components of its momentum, and the probability distribution is

The constant a is given by the normalisation condition. The integrations over p_x, p_y and p_z are separate; by means of the formula

we find a = (2πmT)^−3/2, and the momentum probability distribution takes the final form

(29.3)

Changing from momenta to velocities (p = mv), we can write the corresponding velocity distribution as

(29.4)

This is the Maxwellian distribution (J. C. Maxwell, 1860). It again consists of a product of three independent factors

(29.5)

each of which gives the probability distribution for a single velocity component.

If the body consists of molecules (e.g. a polyatomic gas), then together with the Maxwellian distribution for the individual atoms there is a similar distribution for the translational motion of each molecule as a whole: from the kinetic energy of the molecule we can separate a term which gives the energy of the translational motion, and so the required distribution separates in the form (29.4), where m must now be taken as the total mass of the molecule, and v_x, v_y, v_z as the velocity components of its centre of mass. It should be emphasised that the Maxwellian distribution for the translational motion of molecules can be valid quite independently of the nature of the motion of the atoms within the molecule (and the rotation of the molecule), and in particular when a quantised description of the latter is necessary.^†

The expression (29.4) is written in terms of Cartesian coordinates in “velocity space”. If we change from Cartesian to spherical polar coordinates, the result is

(29.6)

where v is the absolute magnitude of the velocity, and θ and ϕ the polar angle and azimuthal angle which determine the direction of the velocity. Integration with respect to angle gives the probability distribution for the absolute magnitude of the velocity:

(29.7)

It is sometimes convenient to use cylindrical coordinates in velocity space. Then

(29.8)

where v_z is the velocity component along the z-axis, v_r the component perpendicular to that axis, and φ the angle which gives the direction of this component.

Let us calculate the mean kinetic energy of an atom. According to the definition of the mean, and using (29.5), we find for any Cartesian velocity component^†

(29.9)

The mean value of the kinetic energy of the atom is therefore 3T/2. We can thus say that the mean kinetic energy of all the particles in the body in classical statistics is always 3NT/2, where N is the total number of particles.

PROBLEMS

PROBLEM 1

Find the mean value of the nth power of the absolute magnitude of the velocity.

SOLUTION

Using (29.7), we find

In particular, if n is even (= 2r), then

if n = 2r+1, then

SOLUTION

PROBLEM 5

Find the probability distribution for the angular velocities of rotation of molecules.

SOLUTION

Just as for translational motion, we can write the probability distribution for the rotation of each molecule separately (in classical statistics). The kinetic energy of rotation of a molecule regarded as a rigid body (which is permissible, owing to the smallness of the atomic vibrations within the molecule) is

where I₁, I₂, I₃ are the principal moments of inertia, Ω₁, Ω₂, Ω₃ are the components of the angular velocity along the principal axes of inertia, and M₁ = I₁Ω₁, M₂ = I₂Ω₂, M₃ = I₃Ω₃ are the components of the angular momentum, which act as generalised momenta with respect to the velocities Ω₁, Ω₂, Ω₃. The normalised probability distribution for the angular-momentum components is

and for the angular velocity

PROBLEM 6

Find the mean squares of the absolute magnitudes of the angular velocity and angular momentum of a molecule.

SOLUTION

The above distributions give

§ 30 The probability distribution for an oscillator

Let us consider a body whose atoms are executing small oscillations about some equilibrium positions. They may be atoms in a crystal or in a gas molecule; in the latter case the motion of the molecule as a whole does not affect the oscillations of the atoms within it and so does not influence the results.

As we know from mechanics, the Hamiltonian (the energy) of a system consisting of an arbitrary number of particles executing small oscillations can be written as a sum:

where q_α are what are called the normal coordinates of the oscillations (equal to zero at points of equilibrium), p_α = 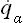are the corresponding generalised momenta, and ω_α are the oscillation frequencies. In other words, E(p, q) is a sum of independent terms, each corresponding to a separate normal oscillation (or, as we say, to an oscillator). In quantum mechanics the same is true of the Hamiltonian operator of the system, so that each oscillator is independently quantised and the energy levels of the system are given by the sums

the n_α being integers.

As a result of these facts the Gibbs distribution for the whole system is a product of independent factors, each giving the statistical distribution for a separate oscillator. In consequence we shall consider a single oscillator in what follows.

Let us determine the probability distribution for the coordinate q of an oscillator;^† the suffix α which gives the number of the oscillator will be omitted henceforward. In classical statistics the solution to this problem would be very simple: since the potential energy of the oscillator is 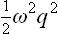, the probability distribution is

or, determining A from the normalisation condition,

(30.1)

the integration with respect to q may be taken from – ∞ to + ∞, since the integral is rapidly convergent.

Let us now consider the solution of this problem in the quantum case. Let Ψ_n(q) be the wave functions of the stationary states of the oscillator, corresponding to the energy levels

If the oscillator is in the nth state, the quantum probability distribution for its coordinate is given by 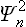(in the present case the functions Ψ_n are real, and so we write simply 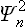instead of the squared modulus |Ψ_n|²). The required statistical probability distribution is obtained by multiplying 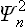by the probability w_n of finding the oscillator in the nth state, and then summing over all possible states.

According to the Gibbs distribution,

where a is a constant. Thus we have the formula

(30.2)

which is, of course, entirely in agreement with the general formula (5.8).

To calculate the sum, we can proceed as follows. With the notation dw_q = _q dq, we form the derivative

Using the momentum operator = i d/dq and the fact that the oscillator momentum has non-zero matrix elements (see Quantum Mechanics, § 23) only for transitions with n → n±1, we can write

Here we have used the relations

between the momentum and coordinate matrix elements. Thus

In the first sum we change the summation suffix from n to n + 1 and use the relations

obtaining

In an exactly similar manner we can prove that

A comparison of the two equations gives

whence

Determining the constant from the normalisation condition, we finally obtain the formula

(30.3)

(F. Bloch, 1932). Thus in the quantum case also the probabilities of various values of the coordinate of an oscillator are distributed according to a law of the form exp (–αq²), but the coefficient α differs from that in the classical case. In the limit ω « T, where the quantisation is unimportant, formula (30.3) becomes (30.1), as we should expect.

In the opposite limiting case ω » T, formula (30.3) becomes

i.e. the purely quantum probability distribution for the coordinate in the ground state of the oscillator.^† This corresponds to the fact that when T « ω the oscillations are hardly excited at all.

The probability distribution for the momentum of the oscillator can be written by analogy with (30.3) without repeating the calculation. The reason is that the problem of quantisation of the oscillator is completely symmetrical as regards the coordinate and the momentum, and the oscillator wave functions in the p representation are the same as its ordinary coordinate wave functions (q being replaced by p/ω; see Quantum Mechanics, § 23, Problem 1. The required distribution is therefore

(30.4)

In the limit of classical mechanics (ω « T) this becomes the usual Maxwellian distribution:

(30.5)

PROBLEM

Determine the coordinate density matrix for a harmonic oscillator.

SOLUTION

The coordinate density matrix for an oscillator in statistical equilibrium is

see the footnote following (5.4). We put q = r+s, q′ = r–s, and calculate the derivative (∂/∂s)_r. As in the similar calculation above, we find

On calculating 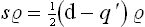in the same way and comparing it with the derivative, we obtain

whence

The function A(r) is determined by the condition that for s = 0, i.e. q = q′ = r, the “diagonal elements” (q, q) of the density matrix agree with (30.3). The final result is

§ 31 The free energy in the Gibbs distribution

According to formula (7.9) the entropy of a body can be calculated as the mean logarithm of its distribution function:

Substituting the Gibbs distribution (28.3) gives

whence log A = (Ē–TS)/T. But the mean energy Ē is just what is meant by the term “energy” in thermodynamics; hence Ē–TS = F and log A = F/T, i.e. the normalisation constant of the distribution is directly related to the free energy of the body.

Thus the Gibbs distribution may be written in the form

(31.1)

and this is the form most frequently used. The same method gives in the classical case, using (7.12), the expression

(31.2)

The normalisation condition for the distribution (31.1) is

(31.3)

This formula is fundamental in thermodynamic applications of the Gibbs distribution. It affords, in principle, the possibility of calculating the thermodynamic functions for any body whose energy spectrum is known.

The sum in the logarithm in (31.3) is usually called the partition function (or sum over states). It is just the trace of the operator exp (–Ĥ/T), where Ĥ is the Hamiltonian of the body:^†

(31.4)

This notation has the advantage that any complete set of wave functions may be used in order to calculate the trace.

A similar formula in classical statistics is obtained from the normalisation condition for the distribution (31.2). First of all, however, we must take account of the following fact, which was unimportant so long as we were discussing the distribution function as such and not relating the normalisation coefficient to a particular quantitative property of the body, viz. its free energy. If, for example, two identical atoms change places, then afterwards the microstate of the body is represented by a different phase point, obtained from the original one by replacing the coordinates and momenta of one atom by those of the other. On the other hand, since the interchanged atoms are identical, the two states of the body are physically identical. Thus a number of points in phase space correspond to one physical microstate of the body. In integrating the distribution (31.2), however, each state must of course be taken only once.^† In other words, we must integrate only over those regions of phase space which correspond to physically different states of the body. This will be denoted by a prime to the integral sign.

Thus we have the formula

(31.5)

here and in all similar cases below, dΓ denotes the volume element in phase space divided by (2π)^s:

(31.6)

Thus the partition function in the quantum formula (31.3) becomes an integral over states. As already mentioned in § 29, the classical energy E(p, q) can always be written as the sum of the kinetic energy K(p) and the potential energy U(q). The kinetic energy is a quadratic function of the momenta, and the integration with respect to the latter can be effected in a general form. The problem of calculating the partition function therefore actually reduces to that of integrating the function e^−U(q)/T with respect to the coordinates.

In the practical calculation of the partition function it is usually convenient to extend the region of integration and include an appropriate correction factor. For example, let us consider a gas of N identical atoms. Then we can integrate with respect to the coordinates of each atom separately, extending the integration over the whole volume occupied by the gas; but the result must be divided by the number of possible permutations of N atoms, which is N!. In other words, the integral ∫′ can be replaced by the integral over all phase space, divided by N!:

(31.7)

PROBLEMS

PROBLEM 1

The potential energy of the interaction between the particles in a body is a homogeneous function of degree n in their coordinates. Using similarity arguments, determine the form of the free energy of such a body in classical statistics.

SOLUTION

In the partition function

we replace each q by λq and each p by λ^n/2p, where λ is an arbitrary constant. If at the same time we replace T by λⁿT, the integrand is unchanged, but the limits of integration with respect to the coordinates are altered: the linear size of the region of integration is multiplied by 1/λ, and so the volume is multiplied by 1/λ³. In order to restore the limits of integration, we must therefore at the same time replace V by λ³V. The result of these changes is to multiply the integral by λ^3N(1+n/2) because of the change of variables in dΓ(s = 3N coordinates and the same number of momenta, N being the number of particles in the body). Thus we conclude that the substitutions V → λ³V, T → λⁿT give

The most general form of function Z(V, T) having this property is

where f is an arbitrary function of one variable.

Hence we find for the free energy an expression of the form

(1)

which involves only one unknown function of one variable; the number N is included in the second term in (1) so that F shall have the necessary property of additivity.

PROBLEM 2

Derive the virial theorem for a macroscopic body for which the potential energy of interaction of the particles is a homogeneous function of degree n in their coordinates.

SOLUTION

Following the derivation of the virial theorem in mechanics (see Mechanics, § 10), we calculate the time derivative of the sum Σr·p, where r and p are the radius vectors and momenta of the particles in the body. Since r = ∂K(p)/∂p and K(p) is a homogeneous function of degree two in the momenta, we have

The particles in the body execute a motion in a finite region of space with velocities which do not become infinite. The quantity Σr·p is therefore bounded and the mean value of its time derivative is zero, so that

where . The derivatives are determined by the forces acting on the particles in the body. In summing over all particles we must take into account not only the forces of interaction between the particles but also the forces exerted on the surface of the body by surrounding bodies:

the surface integral is transformed to a volume integral and we use the fact that div r = 3. Thus we have 2K–nU–3PV = 0 or, in terms of the total energy E = U+K,

(2)

This is the required theorem. It is valid in both classical and quantumtheory. In the classical case, the mean kinetic energy K = 3NT/2, and (2) gives

(3)

This formula could also be derived from the expression (1) for the free energy (Problem 1).

When the particles interact by Coulomb’s law (n = − 1), we have from (2)

This is the limiting case of the relativistic relation

in which the energy E includes the rest energy of the particles in the body; see Fields, § 35.

§ 32 Thermodynamic perturbation theory

In the actual calculation of thermodynamic quantities there occur cases where the energy E(p, q) of a body contains relatively small terms which may be neglected to a first approximation. These may be, for instance, the potential energy of the particles of the body in an external field. The conditions under which such terms may be regarded as small are discussed below.

In these cases a kind of “perturbation theory” may be employed for the calculation of the thermodynamic quantities (R. E. Peierls, 1932). We shall first show how this is to be done when the classical Gibbs distribution is applicable.

We write the energy E(p, q) in the form

(32.1)

where V represents the small terms. To calculate the free energy of the body, we put

(32.2)

in the expansion in powers of V we shall always omit terms above the second order, in order to calculate the corrections only to the first and second orders of approximation. Taking logarithms and again expanding in series, we have to the same accuracy

where F₀ denotes the “unperturbed” free energy, calculated for V = 0.

The resulting integrals are the mean values of the corresponding quantities over the “unperturbed” Gibbs distribution. Taking the averaging in this sense and noticing that , we have finally

(32.3)

Thus the first-order correction to the free energy is just the mean value of the energy perturbation V. The second-order correction is always negative, and is determined by the mean square of the deviation of V from its mean value. In particular, if the mean value is zero, the perturbation reduces the free energy.

A comparison of the terms of the second and first orders in (32.3) enables us to ascertain the condition for this perturbation method to be applicable. Here it must be remembered that both the mean value 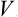and the mean square 〈(V – 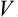)²〉 are roughly proportional to the number of particles; cf. the discussion in § 2 concerning r.m.s. fluctuations of the thermodynamic quantities for macroscopic bodies. We can therefore formulate the desired condition by requiring that the perturbation energy per particle should be small in comparison with T.^†

Let us now carry out the corresponding calculations for the quantum case. Instead of (32.1) we must now use the analogous expression for the Hamiltonian operator:

According to the quantum perturbation theory (see Quantum Mechanics, § 38), the energy levels of the perturbed system are given, correct to the second-order terms, by

(32.4)

where the are the unperturbed energy levels (assumed non-degenerate); the prime to the sum signifies that the term with m = n must be omitted.

This expression is to be substituted in the formula

and expanded in the same way as above. We thus easily obtain

(32.5)

where 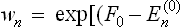is the unperturbed Gibbs distribution.

The diagonal matrix element V_nn is just the mean value of the perturbation energy V in the given (nth) quantum state. The sum

is therefore the value of V averaged both over the quantum state of the body and over the (unperturbed) statistical distribution with respect to the various quantum states. This value gives the correction to the free energy in the first-order approximation, formally the same as the classical result above.

Formula (32.5) may be rewritten as

(32.6)

All the second-order terms in this expression are negative, since w_m – w_n has the same sign as 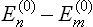. Thus the correction to the free energy in the second-order approximation is negative in the quantum case also.

As in the classical case, the condition for this method to be applicable is that the perturbation energy per particle should be small compared with T. On the other hand, the condition for the applicability of the ordinary quantum perturbation theory (leading to the expression (32.4) for E_n) is, as we know, that the matrix elements of the perturbation should be small compared with the separations of the corresponding energy levels; roughly speaking, the perturbation energy must be small compared with the separations of the energy levels between which allowed transitions can take place.^†

These two conditions are not the same, since the temperature is unrelated to the energy levels of the body. It may happen that the perturbation energy is small compared with T, but is not small, or indeed is even large, compared with the significant separations between energy levels. In such cases the “perturbation theory” for thermodynamic quantities, i.e. formula (32.6), will be applicable while the perturbation theory for the energy levels themselves, i.e. formula (32.4), is not; that is, the limits of convergence of the expansion represented by formula (32.6) may be wider than those of (32.4), from which the former expansion has been derived.

The converse case is, of course, also possible (at sufficiently low temperatures).

Formula (32.6) is considerably simplified if not only the perturbation energy but also the differences between energy levels are small in comparison with T. Expanding the difference w_m – w_n in (32.6) in powers of 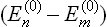, we find in this case

The rule of matrix multiplication gives

and we obtain an expression which is formally exactly the same as formula (32.3). Thus in this case the quantum formula is in formal agreement with the classical formula.^†

§ 33 Expansion in powers of

Formula (31.5) is essentially the first and principal term in an expansion of the quantum formula (31.3) for the free energy in powers of in the quasi-classical case. It is of considerable interest to derive the next non-vanishing term in this expansion (E. P. Wigner, G. E. Uhlenbeck and L. Gropper, 1932).

The problem of calculating the free energy amounts to that of calculating the partition function. For this purpose we use the fact that the latter is the trace of the operator exp (–βĤ) (see (31.4)), with the notation β = 1/T in order to simplify the writing of the involved expressions. The trace of an operator may be calculated by means of any complete set of orthonormal wave functions. For these it is convenient to use the wave functions of free motion of a system of N non-interacting particles in a large but finite volume V. These functions are

(33.1)

where the q_i are the Cartesian coordinates of the particles and the p_i the corresponding momenta, labelled by the suffix i, which takes the values 1, 2, …, s, where s = 3N is the number of degrees of freedom of the system of N particles.

The subsequent calculations apply equally to systems containing identical particles (atoms) and to those where the particles are different. In order to allow in a general manner for a possible difference between the particles, we shall add to the particle mass a suffix indicating the degree of freedom: m_i. Of course the three m_i corresponding to any one particle are always equal.

The existence of identical particles in a body means that, in the quantum theory, exchange effects must be taken into account. This means, first of all, that the wave functions (33.1) must be made symmetrical or antisymmetrical in the particle coordinates, depending on the statistics obeyed by the particles. It is found, however, that this effect leads only to exponentially small terms in the free energy, and so is of no interest. Secondly, the identity of particles in quantum mechanics affects the manner in which the summation over different values of the particle momenta must be carried out. We shall meet this later, for example in calculating partition functions for an ideal quantum gas. The effect produces a term of the third order in in the free energy (as shown later) and so again does not affect the terms of order ² which we shall calculate here. Thus the exchange effects can be ignored in the calculation.

In each of the wave functions (33.1) the momenta p_i have definite constant values. The possible values of each p_i form a dense discrete set (the distances between neighbouring values being inversely proportional to the linear dimensions of the volume occupied by the system). The summation of the matrix elements exp(–βĤ)_pp with respect to all possible values of the momenta may therefore be replaced by integration with respect to p (dp = dp₁ dp₂ … dp_s), bearing in mind that the number of quantum states “belonging” to the volume V^N dp of phase space (all values of the coordinates of each particle in the volume V and values of the momenta in dp) is

We shall use the notation

(33.2)

The required matrix elements are obtained by integrating with respect to all the coordinates:

(33.3)

The partition function is then obtained by integration with respect to the momenta.

Altogether, therefore, we must integrate I over all phase space, or more precisely over those of its regions which correspond to physically different states of the body, as explained in § 31. This is again denoted by a prime to the integral sign:

(33.4)

Let us first calculate I by means of the following procedure. We take the derivative

the operator Ĥ acting on all factors to its right, and expand the right-hand side, using the explicit expression for the Hamiltonian of the body:

(33.5)

where U = U(q₁, q₂, …, q_s) is the potential energy of interaction between all particles in the body. By means of (33.5) we obtain after a straightforward calculation the following equation for I:

where

(33.6)

is the usual classical expression for the energy of the body.

This equation is to be solved with the obvious condition that I = 1 when β = 0. The substitution

(33.7)

gives

(33.8)

with the boundary condition χ = 1 for β = 0.

In order to obtain an expansion in powers of , we solve equation (33.8) by successive approximations, putting

(33.9)

with χ₁ = 0, χ₂ = 0, … for β = 0. Substituting this expansion in equation (33.8) and separating terms in different powers of , we obtain the equations

The first equation gives χ₁, and then the second equation gives χ₂. A simple calculation leads to the results

(33.10)

The required partition function (33.4) is

(33.11)

The term of the first order in in this integral is easily seen to be zero, since the integrand 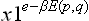in that term is an odd function of the momenta (E(p, q) being quadratic in the momenta and χ₁, by (33.10), linear), and so the result on integrating with respect to momenta is zero. Thus we can write (33.11) as

where 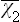is the value of χ₂ averaged over the classical Gibbs distribution:

Substituting this expression for the partition function in formula (31.3), we have for the free energy

or, to the same accuracy,

(33.12)

Here F_cl is the free energy in classical statistics (formula (31.5)).

Thus the next term after the classical expression in the expansion of the free energy is of the second order in . This is not accidental: in equation (33.8), solved here by the method of successive approximations, the quantum constant appears only as i, and so the resulting expansion is one in powers of i; but the free energy, being a real quantity, can contain only powers of i which are real. Thus this expansion of the free energy (ignoring exchange effects) is an expansion in even powers of .

It remains to calculate the mean value 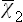. We have seen in § 29 that in classical statistics the probability distributions for the coordinates and momenta are independent. The averaging over momenta and over coordinates can therefore be made separately.

The mean value of the product of two different momenta is clearly zero. The mean value of the square is m_i/β. We can therefore write

where Δ_ik = 1 for i = k and 0 for i ≠ k. Having averaged with respect to momenta by means of this formula, we obtain

(33.13)

The two terms here may be combined, since the mean values are related by the formula

(33.14)

This is easily seen by noticing that

The first term on the right-hand side gives only a surface effect, and since the body is macroscopic this effect may be neglected in comparison with the second term.

Substituting the resulting expression for 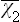in formula (33.12), and replacing β by 1/T, we find the following final expression for the free energy:

(33.15)

We see that the correction to the classical value is always positive, and is determined by the mean squares of the forces acting on the particles. This correction decreases with increasing particle mass and increasing temperature.

According to the above discussion, the next term in the expansion given here would be of the fourth order. This enables us to calculate quite independently the term of order ³ which occurs in the free energy because of the peculiarities of the summation over momenta resulting from the identity of particles in quantum mechanics. The term in question is formally the same as the correction term which appears in a similar calculation for an ideal gas, and is given by formula (56.14):

(33.16)

for a body consisting of N identical particles. The upper sign applies for Fermi statistics and the lower sign for Bose statistics; g is the total degree of degeneracy with respect to the directions of the electron and nuclear angular momenta.

From these formulae we can also obtain the correction terms in the probability distribution functions for the coordinates and momenta of the atoms of the body. According to the general results in § 5, the momentum probability distribution is given by the integral of I with respect to q (see (5.10)):

The term 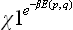in I contains a total derivative with respect to the coordinates, and the integral of it gives a surface effect which can be neglected. Thus we have

The third and fourth terms in the expression (33.10) for χ₂ give a small constant (not involving the momenta) on integration, and this can be neglected in the same approximation. Taking out also the factor ∫ e^−βU dq and including it in the constant coefficient, we have

The mean values which appear here are related by

similarly to (33.14). Hence

(33.17)

This expression can be conveniently rewritten in the following final form:

(33.18)

the bracket in (33.17) being replaced by an exponential function to the same degree of accuracy.

Thus we see that the correction to the classical distribution function for the momenta is equivalent to adding to the kinetic energy in the exponent an expression quadratic in the momenta, with coefficients depending on the law of interaction between the particles in the body.

If it is desired to find the probability distribution for any one momentum p_i, then (33.17) must be integrated with respect to all the other momenta. All the terms involving the squares 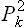will then give constants negligible compared with unity, while the terms containing products of different momenta give zero. The result is, again in exponential form,

(33.19)

Thus the distribution obtained differs from the Maxwellian only in that the true temperature T is replaced by a somewhat higher “effective temperature”:

The same calculations as led to (33.13) give

(33.20)

§ 34 The Gibbs distribution for rotating bodies

The problem of the thermodynamic relations for rotating bodies has already been considered in § 26. Let us now see how the Gibbs distribution is to be formulated for rotating bodies. This will complete the investigation of their statistical properties. As regards the uniform translational motion, Galileo’s relativity principle shows that, as already mentioned in § 26, this motion has only a trivial effect on the statistical properties and so needs no special consideration.

In a system of coordinates rotating with the body, the usual Gibbs distribution is valid; in classical statistics,

(34.1)

where E′(p, q) is the energy of the body in this system, as a function of the coordinates and momenta of its particles, and F′ the free energy in the same system (which, of course, is not the same as the free energy of the body when at rest). The energy E′(p, q) is related to the energy E(p, q) in a fixed system by

(34.2)

where Ω is the angular velocity of rotation and M(p, q) the angular momentum of the body (see § 26). Substituting (34.2) in (34.1), we find the Gibbs distribution for a rotating body in the form^†

(34.3)

In classical statistics the Gibbs distribution for a rotating body can also be represented in another form. To obtain this, we use the following expression for the energy of the body in the rotating coordinate system:

(34.4)

where the v′ are the velocities of the particles relative to the rotating system, and the r their radius vectors (see Mechanics, § 39). Denoting by

(34.5)

the part of the energy which is independent of Ω, we obtain the Gibbs distribution in the form

The function determines the probability corresponding to the element of phase space 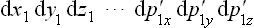, where p′ = mv′ + mΩ × r (see Mechanics, § 39). Since, in obtaining the differentials of the momenta, we must regard the coordinates as constant, dp′ = m dv′, and the probability distribution expressed in terms of the coordinates and velocities of the particle is

(34.6)

where C denotes for brevity the factor (2π)^−s together with the product of the particle masses which appears when we go from the momentum differentials to the velocity differentials.

For a body at rest we have

(34.7)

with the same expression (34.5) for E₀(v, r), now a function of the velocities in the fixed coordinate system. Thus we see that the Gibbs distribution for the coordinates and velocities for a rotating body differs from that for a body at rest only by the additional potential energy . In other words, as regards the statistical properties of the body, the rotation is equivalent to the existence of an external field corresponding to the centrifugal force. The statistical properties are not affected by the Coriolis force.

It should be emphasised, however, that this last result applies only to classical statistics. In the quantum case the expression

(34.8)

gives the statistical operator corresponding to (34.3) for a rotating body. Formally we can reduce this operator to a form analogous to (34.6), the velocities v′ being replaced by the operators , but the components of this vector operator do not commute, unlike those of the operator in the fixed system. The statistical operators corresponding to the expressions (34.6) and (34.7) will therefore in general be markedly different from each other, quite apart from the fact that one of them contains the centrifugal energy.

§ 35 The Gibbs distribution for a variable number of particles

So far we have always tacitly assumed that the number of particles in a body is some given constant, and have deliberately passed over the fact that in reality particles may be exchanged between different subsystems. In other words, the number N of particles in a subsystem will necessarily fluctuate about its mean value. In order to formulate precisely what we mean by the number of particles, we shall use the term subsystem to refer to a part of the system which is enclosed in a fixed volume. Then N will denote the number of particles within that volume.^†

Thus the problem arises of generalising the Gibbs distribution to bodies with a variable number of particles. Here we shall write the formulae for bodies consisting of identical particles; the further generalisation to systems containing different particles is obvious (§ 85).

The distribution function now depends not only on the energy of the quantum state but also on the number N of particles in the body, and the energy levels E_nN are of course themselves different for different N (as indicated by the suffix N). The probability that the body contains N particles and is in the nth state will be denoted by w_nN.

The form of this function can be determined in exactly the same way as the function w_n in § 28. The only difference is that the entropy of the medium is now a function not only of its energy E′ but also of the number N′ of particles in it: S′ = S′(E′, N′). Writing E′ = E⁽⁰⁾–E_nN and N′ = N⁽⁰⁾ – N(where N is the number of particles in the body, and N⁽⁰⁾ the given total number of particles in the entire closed system, which is large compared with N), we have in accordance with (28.2)

the quantity ΔE′ is regarded as constant, as in § 28.

Next, we expand S′ in powers of E_nN and N, again taking only the linear terms. Equation (24.5), in the form

shows that (∂S/∂E)_{V, N} = 1/T, (∂S/∂N)_{E, V} = –μ/T. Hence

the chemical potential μ (and the temperature) being the same for the body and the medium, from the conditions of equilibrium.

Thus we obtain for the distribution function the expression

(35.1)

The normalisation constant A can be expressed in terms of the thermodynamic quantities in the same way as in § 31. The entropy of the body is

and so

But Ē–TS = F, and the difference 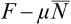is the thermodynamic potential Ω. Thus T log A = Ω, and (35.1) may be rewritten as

(35.2)

This is the final formula for the Gibbs distribution for a variable number of particles.^†

The normalisation condition for the distribution (35.2) requires that the result of summing the w_nN first over all quantum states (for a given N) and then over all values of N should be equal to unity:

Hence we obtain the following expression for the thermodynamic potential Ω:

(35.3)

This formula together with (31.3) can be used to calculate the thermodynamic quantities for specific bodies. Formula (31.3) gives the free energy of the body as a function of T, N and V, and (35.3) gives the potential Ω as a function of T, μ and V.

In classical statistics the probability distribution has the form

where

(35.4)

The variable N is written as a subscript to the distribution function, and the same letter is written as a superscript to the element of phase volume in order to emphasise that a different phase space (of 2s dimensions) corresponds to each value of N. The formula for Ω correspondingly becomes

(35.5)

Finally, we may say a few words concerning the relation between the Gibbs distribution (35.2) for a variable number of particles derived here and the previous distribution (31.1). First of all, it is clear that, for the determination of all the statistical properties of the body except the fluctuations of the total number of particles in it, these two distributions are entirely equivalent. On neglecting the fluctuations of the number N, we obtain Ω + μN = F, and the distribution (35.2) is identical with (31.1).

The relation between the distributions (31.1) and (35.2) is to a certain extent analogous to that between the microcanonical and canonical distributions. The description of a subsystem by means of the microcanonical distribution is equivalent to neglecting the fluctuations of its total energy; the canonical distribution in its usual form (31.1) takes into account these fluctuations. The latter form in turn neglects the fluctuations in the number of particles, and may be said to be “microcanonical with respect to the number of particles”; the distribution (35.2) is “canonical” with respect to both the energy and the number of particles.

Thus all three distributions, the microcanonical and the two forms of the Gibbs distribution, are in principle suitable for determining the thermodynamic properties of the body. The only difference from this point of view lies in the degree of mathematical convenience. In practice the microcanonical distribution is the least convenient and is never used for this purpose. The Gibbs distribution for a variable number of particles is usually the most convenient.

§ 36 The derivation of the thermodynamic relations from the Gibbs distribution

The Gibbs distribution plays a fundamental part throughout statistical physics. We shall therefore give here another justification of it. This distribution has essentially been derived in §§ 4 and 6 directly from Liouville’s theorem. We have seen that the application of Liouville’s theorem (together with considerations of the multiplicativity of distribution functions for subsystems) enables us to deduce that the logarithm of the distribution function of a subsystem must be a linear function of its energy:

(36.1)

the coefficients β being the same for all subsystems in a given closed system (see (6.4), and the corresponding relation (4.5) for the classical case). Hence

using the purely formal notation β = − 1/T, α = F/T, we have an expression of the same form as the Gibbs distribution (31.1). It remains to show that the fundamental thermodynamic relations can be derived from the Gibbs distribution itself, i.e. in a purely statistical manner.

We have already seen that the quantity β, and therefore T, must be the same for all parts of a system in equilibrium. It is also evident that β < 0, i.e. T > 0, since otherwise the normalisation sum Σw_n must diverge: owing to the presence of the kinetic energy of the particles, the energy E_n can take arbitrarily large values. All these properties agree with the fundamental properties of the thermodynamic temperature.

To derive a quantitative relation, we start from the normalisation condition

We differentiate this equation, regarding the left-hand side as a function of T and of various quantities λ₁, λ₂, … which represent the external conditions to which the body considered is subject; these quantities may, for example, determine the shape and size of the volume occupied by the body. The energy levels E_n depend on λ₁, λ₂, … as parameters.

Differentiation gives

where for simplicity only one external parameter is used. Hence

On the left-hand side Σw_n = 1, and on the right-hand side

Using also the formulae F–Ē = –TS and ^†

(36.2)

we have finally

This is the general form for the differential of the free energy.

In the same way we can derive the Gibbs distribution for a variable number of particles. If the number of particles is regarded as a dynamical variable, it is clear that it will be an “integral of the motion”, and additive, for a closed system. We must therefore write

(36.3)

where λ, like β, must be the same for all parts of a system in equilibrium. Putting α = Ω/T, β = −1/T, Γ = μ/^T, we obtain a distribution of the form (35.2), and then by the same method as above we can deduce an expression for the differential of the potential Ω.

^†To avoid misunderstanding, let us mention once more that the w_n (or ) are monotonic functions of energy and need not have maxima for E = Ē. It is the distribution function with respect to energy, obtained by multiplying w_n by dΓ(E)/dE, wich has a sharp maximum at E = Ē.

^†It is assumed that Cartesian coordinates are used.

^†In quantum statistics this statement is not true in general.

^†The Maxwellian distribution clearly applies also to the Brownian motion of particles suspended in a liquid.

^†For reference we shall give the values of the integrals of the form

which often occur in applications of the Maxwellian distribution. The substitution αx² = y gives

where Γ(x) is the gamma function. In particular, if n = 2r with r > 0, then

where (2r–1)!! = 1·3·5· … (2r–1). If r = 0, then

If n = 2r+1, then

The same integral from – ∞ to + ∞ is zero if n = 2r+1 and twice the integral from 0 to ∞ if n = 2r.

^†The normal coordinate has the dimensions cm·g^1/2.

^†This is the squared modulus of the wave function of the ground state of the oscillator.

^†In accordance with the general rules, exp (–Ĥ/T) denotes an operator whose eigenfunctions are the same as those of the operator Ĥ and whose eigenvalues are .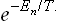

^†This becomes particularly evident if we consider the classical partition function (integral over states) as the limit of the quantum partition function. In the latter the summation is over all the different quantum states, and there is no problem (remembering that, because of the principle of symmetry of wave functions in quantum mechanics, the quantum state is unaffected by interchanges of identical particles).
From the purely classical viewpoint the need for this interpretation of the statistical integration arises because otherwise the statistical weight would no longer be multiplicative, and so the entropy and the other thermodynamic quantities would no longer be additive.

^†In expanding the integrand in (32.2) we have, strictly speaking, expanded in terms of a quantity V/T, which is proportional to the number of particles and is therefore certainly not small, but the further expansion of the logarithm causes the large terms to cancel, and so a series in powers of a small quantity is obtained.

^†These are in general the transitions in which the states of only a small number of particles in the body are changed.

^†The more powerful methods of the “diagram technique”, allowing the whole perturbation theory series to be considered for thermodynamic quantities, will be described in Part 2.

^†The distribution (34.3), like the ordinary Gibbs distribution, is fully in agreement with the result (4.2) derived in § 4 from Liouville’s theorem: the logarithm of the distribution function is a linear function of the energy and angular momentum of the body.

^†In deriving the Gibbs distribution in § 28 we have in essence already understood subsystems in this sense; in going from (28.2) to (28.3) we differentiated the entropy whilst regarding the volume of the body (and therefore of the medium) as constant.

^†This distribution is sometimes called the grand canonical ensemble.

^†If the Hamiltonian Ĥ (and therefore its eigenvalues E_n) depends on a parameter λ, then

see Quantum Mechanics, (11.16). On statistical averaging this gives (36.2).