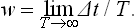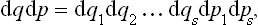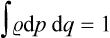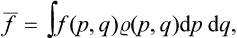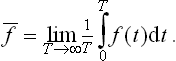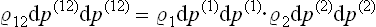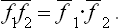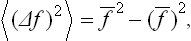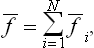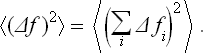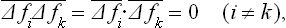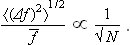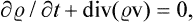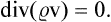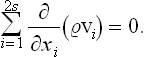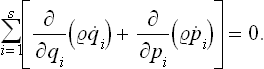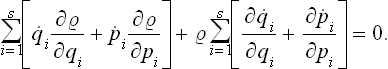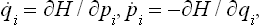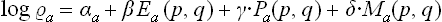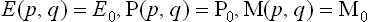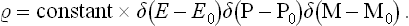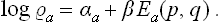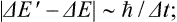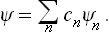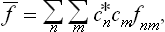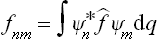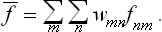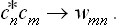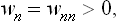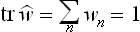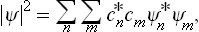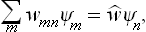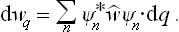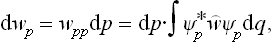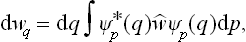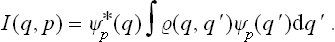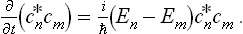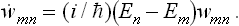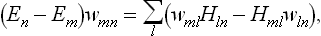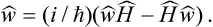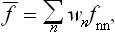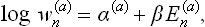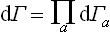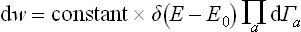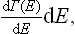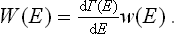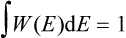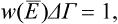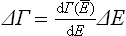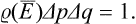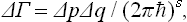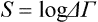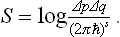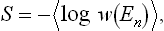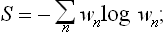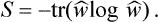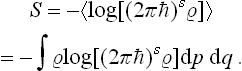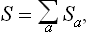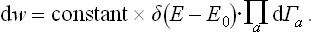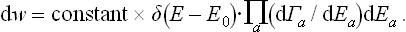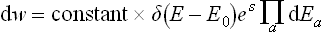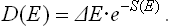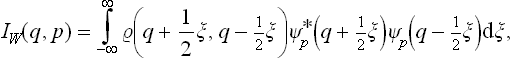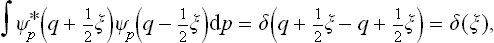THE FUNDAMENTAL PRINCIPLES OF STATISTICAL PHYSICS
Publisher Summary
Statistical physics is the study of special laws that govern the behavior and properties of macroscopic bodies. The general character of these laws does not depend on the mechanics that describes the motion of the individual particles in a body, but their substantiation demands a different argument in the two cases. Information concerning the motion of a mechanical system is obtained by constructing and integrating the equations of motion of the system that are equal in number to its degrees of freedom. These statistical laws resulting from the presence of a large number of particles forming the body cannot be reduced to mechanical laws. They cease to have meaning when applied to mechanical systems with a small number of degrees of freedom. Thus, although the motion of systems with a large number of degrees of freedom obeys the same laws of mechanics as that of systems consisting of a small number of particles, the existence of many degrees of freedom results in laws of a different kind.
§ 1 Statistical distributions
Statistical physics, often called for brevity simply statistics, consists in the study of the special laws which govern the behaviour and properties of macroscopic bodies (that is, bodies formed of a very large number of individual particles, such as atoms and molecules). To a considerable extent the general character of these laws does not depend on the mechanics (classical or quantum) which describes the motion of the individual particles in a body, but their substantiation demands a different argument in the two cases. For convenience of exposition we shall begin by assuming that classical mechanics is everywhere valid.
In principle, we can obtain complete information concerning the motion of a mechanical system by constructing and integrating the equations of motion of the system, which are equal in number to its degrees of freedom. But if we are concerned with a system which, though it obeys the laws of classical mechanics, has a very large number of degrees of freedom, the actual application of the methods of mechanics involves the necessity of setting up and solving the same number of differential equations, which in general is impracticable. It should be emphasised that, even if we could integrate these equations in a general form, it would be completely impossible to substitute in the general solution the initial conditions for the velocities and coordinates of all the particles.
At first sight we might conclude from this that, as the number of particles increases, so also must the complexity and intricacy of the properties of the mechanical system, and that no trace of regularity can be found in the behaviour of a macroscopic body. This is not so, however, and we shall see below that, when the number of particles is very large, new types of regularity appear.
These statistical laws resulting from the very presence of a large number of particles forming the body cannot in any way be reduced to purely mechanical laws. One of their distinctive features is that they cease to have meaning when applied to mechanical systems with a small number of degrees of freedom. Thus, although the motion of systems with a very large number of degrees of freedom obeys the same laws of mechanics as that of systems consisting of a small number of particles, the existence of many degrees of freedom results in laws of a different kind.
The importance of statistical physics in many other branches of theoretical physics is due to the fact that in Nature we continually encounter macroscopic bodies whose behaviour can not be fully described by the methods of mechanics alone, for the reasons mentioned above, and which obey statistical laws.
In proceeding to formulate the fundamental problem of classical statistics, we must first of all define the concept of phase space, which will be constantly used hereafter.
Let a given macroscopic mechanical system have s degrees of freedom: that is, let the position of points of the system in space be described by s coordinates, which we denote by qi, the suffix i taking the values 1, 2,…, s. Then the state of the system at a given instant will be defined by the values at that instant of the s coordinates qi and the s corresponding velocities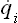 
. In statistics it is customary to describe a system by its coordinates and momenta pi, not velocities, since this affords a number of very important advantages. The various states of the system can be represented mathematically by points in phase space (which is, of course, a purely mathematical concept); the coordinates in phase space are the coordinates and momenta of the system considered. Every system has its own phase space, with a number of dimensions equal to twice the number of degrees of freedom. Any point in phase space, corresponding to particular values of the coordinates qi and momenta pi of the system, represents a particular state of the system. The state of the system changes with time, and consequently the point in phase space representing this state (which we shall call simply the phase point of the system) moves along a curve called the phase trajectory.
Let us now consider a macroscopic body or system of bodies, and assume that the system is closed, i.e. does not interact with any other bodies. A part of the system, which is very small compared with the whole system but still macroscopic, may be imagined to be separated from the rest; clearly, when the number of particles in the whole system is sufficiently large, the number in a small part of it may still be very large. Such relatively small but still macroscopic parts will be called subsystems. A subsystem is again a mechanical system, but not a closed one; on the contrary, it interacts in various ways with the other parts of the system. Because of the very large number of degrees of freedom of the other parts, these interactions will be very complex and intricate. Thus the state of the subsystem considered will vary with time in a very complex and intricate manner.
An exact solution for the behaviour of the subsystem can be obtained only by solving the mechanical problem for the entire closed system, i.e. by setting up and solving all the differential equations of motion with given initial conditions, which, as already mentioned, is an impracticable task. Fortunately, it is just this very complicated manner of variation of the state of subsystems which, though rendering the methods of mechanics inapplicable, allows a different approach to the solution of the problem.
A fundamental feature of this approach is the fact that, because of the extreme complexity of the external interactions with the other parts of the system, during a sufficiently long time the subsystem considered will be many times in every possible state. This may be more precisely formulated as follows. Let Δp Δq denote some small “volume” of the phase space of the subsystem, corresponding to coordinates qi and momenta pi lying in short intervals Δqi, and Δpi. We can say that, in a sufficiently long time T, the extremely intricate phase trajectory passes many times through each such volume of phase space. Let Δt be the part of the total time T during which the subsystem was in the given volume of phase space ΔpΔq.† When the total time T increases indefinitely, the ratio Δt/T tends to some limit
This quantity may clearly be regarded as the probability that, if the subsystem is observed at an arbitrary instant, it will be found in the given volume of phase space Δp Δq.
On taking the limit of an infinitesimal phase volume‡
we can define the probability dw of states represented by points in this volume element, i.e. the probability that the coordinates qi and momenta pi have values in given infinitesimal intervals between qi, pi and qi + dqi, pi + dpi. This probability dw may be written
where 
(p1, …, ps, q1, …, qs) is a function of all the coordinates and momenta; we shall usually write for brevity (p, q) or even simply. The function , which represents the “density” of the probability distribution in phase space, is called the statistical distribution function, or simply the distribution function, for the body concerned. This function must obviously satisfy the normalisation condition
(the integral being taken over all phase space), which simply expresses the fact that the sum of the probabilities of all possible states must be unity.
The following circumstance is extremely important in statistical physics. The statistical distribution of a given subsystem does not depend on the initial state of any other small part of the same system, since over a sufficiently long time the effect of this initial state will be entirely outweighed by the effect of the much larger remaining parts of the system. It is also independent of the initial state of the particular small part considered, since in time this part passes through all possible states, any of which can be taken as the initial state. Without having to solve the mechanical problem for a system (taking account of initial conditions), we can therefore find the statistical distribution for small parts of the system.
The determination of the statistical distribution for any subsystem is in fact the fundamental problem of statistical physics. In speaking of “small parts” of a closed system, we must bear in mind that the macroscopic bodies with which we have to deal are usually themselves such “small parts” of a large closed system consisting of these bodies together with the external medium which surrounds them.
If this problem is solved and the statistical distribution for a given subsystem is known, we can calculate the probabilities of various values of any physical quantities which depend on the states of the subsystem (i.e. on the values of its coordinates q and momenta p). We can also calculate the mean value of any such quantity f(p, q), which is obtained by multiplying each of its possible values by the corresponding probability and integrating over all states. Denoting the averaging by a bar, we can write
from which the mean values of various quantities can be calculated by using the statistical distribution function.†
The averaging with respect to the distribution function (called statistical averaging) frees us from the necessity of following the variation with time of the actual value of the physical quantity f(p, q) in order to determine its mean value. It is also obvious that, by the definition (1.1) of the probability, the statistical averaging is exactly equivalent to a time averaging. The latter would involve following the variation of the quantity with time, establishing the function f = f(t) and determining the required mean value as
The foregoing discussion shows that the deductions and predictions concerning the behaviour of macroscopic bodies which are made possible by statistical physics are probabilistic. In this respect statistical physics differs from (classical) mechanics, the deductions of which are entirely deterministic. It should be emphasised, however, that the probabilistic nature of the results of classical statistics is not an inherent property of the objects considered, but simply arises from the fact that these results are derived from much less information than would be necessary for a complete mechanical description (the initial values of the coordinates and momenta are not needed).
In practice, however, when statistical physics is applied to macroscopic bodies, its probabilistic nature is not usually apparent. The reason is that, if any macroscopic body (in external conditions independent of time) is observed over a sufficiently long period of time, it is found that all physical quantities describing the body are practically constant (and equal to their mean values) and undergo appreciable changes relatively very rarely; we mean, of course, macroscopic quantities describing the body as a whole or macroscopic parts of it, but not individual particles.† This result, which is fundamental to statistical physics, follows from very general considerations (to be discussed in § 2) and becomes more and more nearly valid as the body considered becomes more complex and larger. In terms of the statistical distribution, we can say that, if by means of the function (p, q) we construct the probability distribution function for various values of the quantity f(p, q), this function will have an extremely sharp maximum for 
, and will be appreciably different from zero only in the immediate vicinity of this point.
Thus, by enabling us to calculate the mean values of quantities describing macroscopic bodies, statistical physics enables us to make predictions which are valid to very high accuracy for by far the greater part of any time interval which is long enough for the effect of the initial state of the body to be entirely eliminated. In this sense the predictions of statistical physics become practically determinate and not probabilistic. (For this reason, we shall henceforward almost always omit the bar when using mean values of macroscopic quantities.)
If a closed macroscopic system is in a state such that in any macroscopic subsystem the macroscopic physical quantities are to a high degree of accuracy equal to their mean values, the system is said to be in a state of statistical equilibrium (or thermodynamic or thermal equilibrium). It is seen from the foregoing that, if a closed macroscopic system is observed for a sufficiently long period of time, it will be in a state of statistical equilibrium for much the greater part of this period. If, at any initial instant, a closed macroscopic system was not in a state of statistical equilibrium (if, for example, it was artificially disturbed from such a state by means of an external interaction and then left to itself, becoming again a closed system), it will necessarily enter an equilibrium state. The time within which it will reach statistical equilibrium is called the relaxation time. In using the term “sufficiently long” intervals of time, we have meant essentially times long compared with the relaxation time.
The theory of processes relating to the attainment of an equilibrium state is called kinetics. It is not part of statistical physics proper, which deals only with systems in statistical equilibrium.
§ 2 Statistical independence
The subsystems discussed in § 1 are not themselves closed systems; on the contrary, they are subject to the continuous interaction of the remaining parts of the system. But since these parts, which are small in comparison with the whole of the large system, are themselves macroscopic bodies also, we can still suppose that over not too long intervals of time they behave approximately as closed systems. For the particles which mainly take part in the interaction of a subsystem with the surrounding parts are those near the surface of the subsystem; the relative number of such particles, compared with the total number of particles in the subsystem, decreases rapidly when the size of the subsystem increases, and when the latter is sufficiently large the energy of its interaction with the surrounding parts will be small in comparison with its internal energy. Thus we may say that the subsystems are quasi-closed. It should be emphasised once more that this property holds only over not too long intervals of time. Over a sufficiently long interval of time, the effect of interaction of subsystems, however weak, will ultimately appear. Moreover, it is just this relatively weak interaction which leads finally to the establishment of statistical equilibrium.
The fact that different subsystems may be regarded as weakly interacting has the result that they may also be regarded as statistically independent. By statistical independence we mean that the state of one subsystem does not affect the probabilities of various states of the other subsystems.
Let us consider any two subsystems, and let dp(1) dq(1) and dp(2) dq(2) be volume elements in their phase spaces. If we regard the two subsystems together as one composite subsystem, then the statistical independence of the subsystems signifies mathematically that the probability of the composite subsystem’s being in its phase volume element dp(12) dq(12) = dp(1) dq(1). dp(2) dq(2) can be written as the product of the probabilities for the two subsystems to be respectively in dp(1) dq(1) and dp(2) dq(2), each of these probabilities depending only on the coordinates and momenta of the subsystem concerned. Thus we can write
or
where 12 is the statistical distribution of the composite subsystem, and 1, 2 the distribution functions of the separate subsystems. A similar relation is valid for a group of several subsystems.†
The converse statement is clearly also true: if the probability distribution for a compound system is a product of factors, each of which depends only on quantities describing one part of the system, then the parts concerned are statistically independent, and each factor is proportional to the probability of the state of the corresponding part.
If f1 and f2 are two physical quantities relating to two different subsystems, then from (2.1) and the definition (1.5) of mean values it follows immediately that the mean value of the product f1f2 is equal to the product of the mean values of the quantities f1 and f2 separately:
Let us consider a quantity f relating to a macroscopic body or to a part of it. In the course of time this quantity varies, fluctuating about its mean value. We may define a quantity which represents the average range of this fluctuation. The mean value of the difference Δf = f—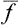
is not suitable for this purpose, since the quantity f varies from its mean value in both directions, and the difference f—
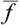, which is alternately positive and negative, has mean value zero regardless of how often f undergoes considerable deviations from its mean value. The required characteristic may conveniently be defined as the mean square of this difference. Since (Δf)2 is always positive, its mean value tends to zero only if (Δf)2 itself tends to zero; that is, the mean value is small only when the probability of considerable deviations of f from 
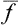is small. The quantity 〈(Δf)2〉1/2 is called the root-mean-square (r.m.s.) fluctuation of the quantity f. Multiplying out the square (f—
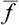)2 shows that
i.e. the r.m.s. fluctuation is determined by the difference between the mean square of the quantity and the square of its mean.
The ratio 〈(Δf)2〉1/2/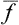
is called ther relative fluctuation of the quantity f. The smaller this ratio is, the more negligible is the proportion of time during which the body is in states where the deviation of f from its mean value is a considerable fraction of the mean value.
We shall show that the relative fluctuations of physical quantities decrease rapidly when the size of the bodies (that is, the number of particles) to which they relate increases. To prove this, we first note that the majority of quantities of physical interest are additive. This property is a consequence of the fact that the various parts of a body are quasi-closed systems, and signifies that the value of such a quantity for the whole body is the sum of its values for the various (macroscopic) parts of the body. For example, since the internal energies of these parts are, as shown above, large compared with their interaction energies, it is sufficiently accurate to assume that the energy of the whole body is equal to the sum of the energies of its parts.
Let f be such an additive quantity. We imagine the body concerned to be divided into a large number N of approximately equal small parts. Then
where the quantities fi relate to the individual parts of the body.
It is clear that, as the size of the body increases,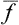 
increases approximately in proportion to N. Let us also determine the r.m.s. fluctuation of f. We have
Because of the statistical independence of the different parts of the body, the mean values of the products ΔfiΔfk are
since each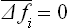 
. Hence
It follows that, as N increases, the mean square 〈(Δf)2〉 also increases in proportion to N. The relative fluctuation is therefore inversely proportional to √N:
On the other hand, if we consider a homogeneous body to be divided into parts of a given small size, it is clear that the number of parts will be proportional to the total number of particles (molecules) in the body. Hence the result can also be stated by saying that the relative fluctuation of any additive quantity f decreases inversely as the square root of the number of particles in a macroscopic body, and so, when the number of these is sufficiently large, the quantity f itself may be regarded as practically constant in time and equal to its mean value. This conclusion has already been used in § 1.
§ 3 Liouville’s theorem
Let us now return to a further study of the properties of the statistical distribution function, and suppose that a subsystem is observed over a very long interval of time, which we divide into a very large (in the limit, infinite) number of equal short intervals between instants t1, t2, …. At each of these instants the subsystem considered is represented in its phase space by a point A1, A2, …. The set of points thus obtained is distributed in phase space with a density which in the limit is everywhere proportional to the distribution function (p, q). This follows from the significance of the latter function as determining the probabilities of various states of the subsystem.
Instead of considering points representing states of one subsystem at different instants t1, t2, …, we may consider simultaneously, in a formal manner, a very large (in the limit, infinite) number of exactly identical subsystems,† which at some instant, say t = 0, are in states represented by the points A1, A2, ….
We now follow the subsequent movement of the phase points which represent the states of these subsystems over a not too long interval of time, such that a quasi-closed subsystem may with sufficient accuracy be regarded as closed. The movement of the phase points will then obey the equations of motion, which involve the coordinates and momenta only of the particles in the subsystem.
It is clear that at any instant t these points will be distributed in phase space according to the same distribution function (p, q), in just the same way as at t = 0. In other words, as the phase points move about in the course of time, they remain distributed with a density which is constant at any given point and is proportional to the corresponding value of .
This movement of phase points may be formally regarded as a steady flow of a “gas” in phase space of 2s dimensions, and the familiar equation of continuity may be applied, which expresses the constancy of the total number of “particles” (in this case, phase points) in the gas. The ordinary equation of continuity is
where is the density and v the velocity of the gas. For steady flow, we have
For a space of 2s dimensions, this will become
In the present case the “coordinates” xi are the coordinates q and momeiua p, and the “velocities” vi =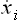
are the time derivatives 
and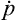 
given by the equations of motion. Thus we have
Expanding the derivatives gives
With the equations of motion in Hamilton’s form:
where H = H(p, q) is the Hamiltonian for the subsystem considered, we see that
The second term in (3.1) is therefore identically zero. The first term is just the total time derivative of the distribution function. Thus
We therefore reach the important conclusion that the distribution function is constant along the phase trajectories of the subsystem. This is Liouville’s theorem. Since quasi-closed subsystems are under dicussion, the result is valid only for not too long intervals of time, during which the subsystem behaves as if closed, to a sufficient approximation.
§ 4 The significance of energy
It follows at once from Liouville’s theorem that the distribution function must be expressible entirely in terms of combinations of the variables p and q which remain constant when the subsystem moves as a closed subsystem. These combinations are the mechanical invariants or integrals of the motion, which are the first integrals of the equations of motion. We may therefore say that the distribution function, being a function of the mechanical invariants, is itself an integral of the motion.
It proves possible to restrict very considerably the number of integrals of the motion on which the distribution function can depend. To do this, we must take into account the fact that the distribution 12 for a combination of two subsystems is equal to the product of the distribution functions 1 and 2 of the two subsystems separately: 12 = 12. Hence
so that the logarithm of the distribution function is an additive quantity. We therefore reach the conclusion that the logarithm of the distribution function must be not merely an integral of the motion, but an additive integral of the motion.
As we know from mechanics, there exist only seven independent additive integrals of the motion: the energy, the three components of the momentum vector and the three components of the angular momentum vector. We shall denote these quantities for the ath subsystem (as functions of the coordinates and momenta of the particles in it) by Ea(p, q), Pa(p, q), Ma(p, q) respectively. The only additive combination of these quantities is a linear combination of the form
with constant coefficients αa, β, γ, δ, of which β, γ, δ must be the same for all subsystems in a given closed system.
We shall return in Chapter III to a detailed study of the distribution (4.2); here we need note only the following points. The coefficient αa is just the normalisation constant, given by the condition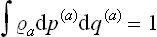 
. The constants β, γ, δ, involving seven independent quantities altogether, may be determined from the seven constant values of the additive integrals of the motion for the whole closed system. Thus we reach a conclusion very important in statistical physics. The values of the additive integrals of the motion (energy, momentum and angular momentum) completely define the statistical properties of a closed system, i.e. the statistical distribution of any of its subsystems, and therefore the mean values of any physical quantities relating to them. These seven additive integrals of the motion replace the unimaginable multiplicity of data (initial conditions) which would be required in the approach from mechanics.
The above arguments enable us at once to set up a simple distribution function suitable for describing the statistical properties of a closed system. Since, as we have seen, the values of non-additive integrals of the motion do not affect these properties, the latter can be described by any function which depends only on the values of the additive integrals of the motion for the system and which satisfies Liouville’s theorem. The simplest such function is = constant for all points in phase space which correspond to given constant values of the energy (E0), momentum (P0) and angular momentum (M0) of the system (regardless of the values of the non-additive integrals) and = 0 at all other points. It is clear that a function so defined will certainly remain constant along a phase trajectory of the system, i.e. will satisfy Liouville’s theorem.
This formulation, however, is not quite exact. The reason is that the points defined by the equations
form a manifold of only 2s—7 dimensions, not 2s like the phase volume. Consequently, if the integral ∫ dp dq is to be different from zero, the function (p, q) must become infinite at these points. The correct way of writing the distribution function for a closed system is
The presence of the delta functions† ensures that is zero at all points in phase space where one or more of the quantities E, P, M is not equal to the given value E0, P0 or M0. The integral of over the whole of a phase volume which includes all or part of the above-mentioned manifold of points is finite. The distribution (4.4) is called microcanonical.‡
The momentum and angular momentum of a closed system depend on its motion as a whole (uniform translation and uniform rotation). We can therefore say that the statistical state of a system executing a given motion depends only on its energy. In consequence, energy is of exceptional importance in statistical physics.
In order to exclude the momentum and angular momentum from the subsequent discussion we may use the following device. We imagine the system to be enclosed in a rigid “box” and take coordinates such that the “box” is at rest. Under these conditions the momentum and angular momentum are not integrals of the motion, and the only remaining additive integral of the motion is the energy. The presence of the “box”, on the other hand, clearly does not affect the statistical properties of small parts of the system (subsystems). Thus for the logarithms of the distribution functions of the subsystems, instead of (4.2), we have the still simpler expressions
The microcanonical distribution for the whole system is
So far we have assumed that the closed system as a whole is in statistical equilibrium; that is, we have considered it over times long compared with its relaxation time. In practice, however, it is usually necessary to discuss a system over times comparable with or even short relative to the relaxation time. For large systems this can be done, owing to the existence of what are called partial (or incomplete) equilibria as well as the complete statistical equilibrium of the entire closed system. Such equilibria occur because the relaxation time increases with the size of the system, and so the separate small parts of the system attain the equilibrium state considerably more quickly than equilibrium is established between these small parts. This means that each small part of the system is described by a distribution function of the form (4.2), with the parameters β, γ, δ of the distribution having different values for different parts. In such a case the system is said to be in partial equilibrium. In the course of time, the partial equilibrium gradually becomes complete, and the parameters β, γ, δ for each small part slowly vary and finally become equal throughout the closed system.
Another kind of partial equilibrium is also of frequent occurrence, namely that resulting from a difference in the rates of the various processes occurring in the system, not from a considerable difference in relaxation time between the system and its small parts. One obvious example is the partial equilibrium in a mixture of several substances involved in a chemical reaction. Owing to the comparative slowness of chemical reactions, equilibrium as regards the motion of the molecules will be reached, in general, considerably more rapidly than equilibrium as regards reactions of molecules, i.e. as regards the composition of the mixture. This enables us to regard the partial equilibria of the mixture as equilibria at a given (actually non-equilibrium) chemical composition.
The existence of partial equilibria leads to the concept of macroscopic states of a system. Whereas a mechanical microscopic description of the system specifies the coordinates and momenta of every particle in the system, a macroscopic description is one which specifies the mean values of the physical quantities determining a particular partial equilibrium, for instance the mean values of quantities describing separate sufficiently small but macroscopic parts of the system, each of which may be regarded as being in a separate equilibrium.
§ 5 The statistical matrix
Turning now to the distinctive features of quantum statistics, we may note first of all that the purely mechanical approach to the problem of determining the behaviour of a macroscopic body in quantum mechanics is of course just as hopeless as in classical mechanics. Such an approach would require the solution of Schrödinger’s equation for a system consisting of all the particles in the body, a problem still more hopeless, one might even say, than the integration of the classical equations of motion. But even if it were possible in some particular case to find a general solution of Schrödinger’s equation, it would be utterly impossible to select and write down the particular solution satisfying the precise conditions of the problem and specified by particular values of an enormous number of different quantum numbers. Moreover, we shall see below that for a macroscopic body the concept of stationary states itself becomes to some extent arbitrary, a fact of fundamental significance.
Let us first elucidate some purely quantum-mechanical features of macroscopic bodies as compared with systems consisting of a relatively small number of particles.
These features amount to an extremely high density of levels in the energy eigenvalue spectrum of a macroscopic body. The reason for this is easily seen if we note that, because of the very large number of particles in the body, a given quantity of energy can, roughly speaking, be “distributed” in innumerable ways among the various particles. The relation between this fact and the high density of levels becomes particularly clear if we take as an example a macroscopic body consisting of a “gas” of N particles which do not interact at all, enclosed in some volume. The energy levels of such a system are just the sums of the energies of the individual particles, and the energy of each particle can range over an infinite series of discrete values.† It is clear that, on choosing in all possible ways the values of the N terms in this sum, we shall obtain a very large number of possible values of the energy of the system in any appreciable finite part of the spectrum, and these values will therefore lie very close together.
It may be shown (see (7.18)) that the number of levels in a given finite range of the energy spectrum of a macroscopic body increases exponentially with the number of particles in the body, and the separations between levels are given by numbers of the form 10−N (where N is a number of the order of the number of particles in the body), whatever the units, since a change in the unit of energy has no effect on such a fantastically small number.†
In consequence of the extremely high density of levels, a macroscopic body in practice can never be in a strictly stationary state. First of all, it is clear that the value of the energy of the system will always be “broadened” by an amount of the order of the energy of interaction between the system and the surrounding bodies. The latter is very large in comparison with the separations between levels, not only for quasi-closed subsystems but also for systems which from any other aspect could be regarded as strictly closed. In Nature, of course, there are no completely closed systems, whose interaction with any other body is exactly zero; and whatever interaction does exist, even if it is so small that it does not affect other properties of the system, will still be very large in comparison with the infinitesimal intervals in the energy spectrum.
In addition to this, there is another fundamental reason why a macroscopic body in practice cannot be in a stationary state. It is known from quantum mechanics that the state of a system described by a wave function is the result of some process of interaction of the system with another system which obeys classical mechanics to a sufficient approximation. In this respect the occurrence of a stationary state implies particular properties of the system. Here we must distinguish between the energy E of the system before the interaction and the energy E’ of the state which results from the interaction. The uncertainties ΔE and ΔE’ in the quantities E and E’ are related to the duration Δt of the interaction process by the formula
see Quantum Mechanics, § 44. The two errors ΔE and ΔE’ are in general of the same order of magnitude, and analysis shows that we cannot make ΔE’ « ΔE. We can therefore say that ΔE’ ˜ ħ/Δt. In order that the state may be regarded as stationary, the uncertainty ΔE’ must certainly be small in comparison with the separations between adjoining levels. Since the latter are extremely small, we see that, in order to bring the macroscopic body into a particular stationary state, an extremely long time Δt ˜ ħ/ΔE’ would be necessary. In other words, we again conclude that strictly stationary states of a macroscopic body cannot exist.
To describe the state of a macroscopic body by a wave function at all is impracticable, since the available data concerning the state of such a body are far short of the complete set of data necessary to establish its wave function. Here the position is somewhat similar to that which occurs in classical statistics, where the impossibility of taking account of the initial conditions for every particle in a body makes impossible an exact mechanical description of its behaviour; the analogy is imperfect, however, since the impossibility of a complete quantum-mechanical description and the lack of a wave function describing a macroscopic body may, as we have seen, possess a much more profound significance.
The quantum-mechanical description based on an incomplete set of data concerning the system is effected by means of what is called a density matrix; see Quantum Mechanics, § 14. A knowledge of this matrix enables us to calculate the mean value of any quantity describing the system, and also the probabilities of various values of such quantities. The incompleteness of the description lies in the fact that the results of various kinds of measurement which can be predicted with a certain probability from a knowledge of the density matrix might be predictable with greater or even complete certainty from a complete set of data for the system, from which its wave function could be derived.
We shall not pause to write out here the formulae of quantum mechanics relating to the density matrix in the coordinate representation, since this representation is seldom used in statistical physics, but we shall show how the density matrix may be obtained directly in the energy representation, which is necessary for statistical applications.
Let us consider some subsystem, and define its “stationary states” as the states obtained when all interactions of the subsystem with the surrounding parts of a closed system are entirely neglected. Let Ψn(q) be the normalised wave functions of these states (without the time factor), q conventionally denoting the set of all coordinates of the subsystem, and the suffix n the set of all quantum numbers which distinguish the various stationary states; the energies of these states will be denoted by En.
Let us assume that at some instant the subsystem is in a completely described state with wave function Ψ. The latter may be expanded in terms of the functions Ψn(q), which form a complete set; we write the expansion as
The mean value of any quantity f in this state can be calculated from the coefficients cn by means of the formula
where
are the matrix elements of the quantity f(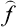
being the corresponding operator).
The change from the complete to the incomplete quantum-mechanical description of the subsystem may be regarded as a kind of averaging over its various Ψ states. In this averaging, the products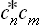 
give a double set (two suffixes) of quantities, which we denote by wmn and which cannot be expressed as products of any quantities forming a single set. The mean value of f is now given by
The set of quantities wmn (which in general are functions of time) is the density matrix in the energy representation; in statistical physics it is called the statistical matrix.†
If we regard the wmn as the matrix elements of some statistical operator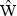 
, then the sum 
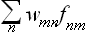will be a diagonal matrix element of the operator product 
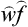, and the mean value 
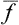becomes the trace (sum of diagonal elements) of this operator:
This formula has the advantage of enabling us to calculate with any complete set of orthonormal wave functions: the trace of an operator is independent of the particular set of functions with respect to which the matrix elements are defined; see Quantum Mechanics, § 12.
The other expressions of quantum mechanics which involve the quantities cn are similarly modified, the products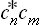 
being everywhere replaced by the “averaged values” wmn:
For example, the probability that the subsystem is in the nth state is equal to the corresponding diagonal element wmn of the density matrix (instead of the squared modulus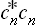 
). It is evident that these elements, which we shall denote by wn, are always positive:
and satisfy the normalisation condition
(corresponding to the condition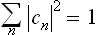 
).
It must be emphasised that the averaging over various Ψ states, which we have used in order to illustrate the transition from a complete to an incomplete quantum-mechanical description, has only a very formal significance. In particular, it would be quite incorrect to suppose that the description by means of the density matrix signifies that the subsystem can be in various Ψ states with various probabilities and that the averaging is over these probabilities. Such a treatment would be in conflict with the basic principles of quantum mechanics.
The states of a quantum-mechanical system that are described by wave functions are sometimes called pure states, as distrinct from mixed states, which are described by a density matrix. Care should, however, be taken not to misunderstand the latter term in the way indicated above.
The averaging by means of the statistical matrix according to (5.4) has a twofold nature. It comprises both the averaging due to the probabilistic nature of the quantum description (even when as complete as possible) and the statistical averaging necessitated by the incompleteness of our information concerning the object considered. For a pure state only the first averaging remains, but in statistical cases both types of averaging are always present. It must be borne in mind, however, that these constituents cannot be separated; the whole averaging procedure is carried out as a single operation, and cannot be represented as the result of successive averagings, one purely quantum-mechanical and the other purely statistical.
The statistical matrix in quantum statistics takes the place of the distribution function in classical statistics. The whole of the discussion in the previous sections concerning classical statistics and the, in practice, deterministic nature of its predictions applies entirely to quantum statistics also. The proof given in § 2 that the relative fluctuations of additive physical quantities tend to zero as the number of particles increases made no use of any specific properties of classical mechanics, and so remains entirely valid in the quantum case. We can therefore again assert that macroscopic quantities remain practically equal to their mean values.
In classical statistics the distribution function (p, q) gives directly the probability distribution of the various values of the coordinates and momenta of the particles of the body. In quantum statistics this is no longer true; the quantities wn give only the probabilities of finding the body in a particular quantum state, with no direct indication of the values of the coordinates and momenta of the particles.
From the very nature of quantum mechanics, the statistics based on it can deal only with the determination of the probability distribution for the coordinates and momenta separately, not together, since the coordinates and momenta of a particle cannot simultaneously have definite values. The required probability distributions must reflect both the statistical uncertainty and the uncertainty inherent in the quantum-mechanical description. To find these distributions, we repeat the arguments given above. We first assume that the body is in a pure quantum state with the wave function (5.1). The probability distribution for the coordinates is given by the squared modulus
so that the probability that the coordinates have values in a given interval dq = dq1 dq2 … dqs is dwq = | Ψ |2 dq. For a mixed state, the products 
are replaced by the elements wmn of the statistical matrix, and | Ψ |2 thus becomes
By the definition of the matrix elements,
and so
Thus we have the following formula for the coordinate probability distribution:
In this expression the functions Ψn may be any complete set of normalised wave functions.
Let us next determine the momentum probability distribution. The quantum states in which all the momenta have definite values correspond to free motion of all the particles. We denote the wave functions of these states by Ψp(q), the suffix p conventionally representing the set of values of all the momenta. As we know, the diagonal elements of the density matrix are the probabilities that the system is in the corresponding quantum states. Hence, having determined the density matrix with respect to the set of functions Ψp, we obtain the required momentum probability distribution from the formula†
where dp = dp1 dp2 … dps.
It is interesting that both distributions (coordinate and momentum) can be obtained by integrating the same function
Integration of this expression with respect to q gives the momentum distribution (5.9). Integration with respect to p gives
in agreement with the general definition (5.8). Note also that the function (5.10) can be expressed in terms of the coordinate density matrix (q, q’) by
It must be emphasised, however, that this does not at all imply that the function I(q, p) may be regarded as a probability distribution for coordinates and momenta simultaneously; the expression (5.10) is in any case complex, quite apart from the fact that such a treatment would altogether contradict the fundamental principles of quantum mechanics.‡
§ 6 Statistical distributions in quantum statistics
In quantum mechanics a theorem can be proved which is analogous to Liouville’s theorem derived in § 3 on the basis of classical mechanics.
To do this, we first derive a general equation of quantum mechanics which gives the time derivative of the statistical matrix of any (closed) system.† Following the method used in § 5, we first assume that the system is in a pure state with a ware function represented in the form of a series (5.1). Since the system is closed, its wave function will have the same form at all subsequent instants, but the coefficients cn will depend on the time, being proportional to factors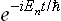 
. We therefore have
The change to the statistical matrix in the general case of mixed states is now effected by replacing the products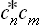 
by wmn, and this gives the required equation:
This equation can be written in a general operator form by noticing that
where Hmn are the matrix elements of the Hamiltonian Ĥ of the system; this matrix is diagonal in the energy representation, which we are using. Hence
It should be pointed out that this expression differs in sign from the usual quantum-mechanical expression for the operator of the time derivative of a quantity.
We see that, if the time derivative of the statistical matrix is zero, the operator 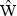must commute with the Hamiltonian of the system. This result is the quantum analogue of Liouville’s theorem: in classical mechanics the requirement of a stationary distribution function has the result that w is an integral of the motion, while the commutability of the operator of a quantity with the Hamiltonian is just the condition, in quantum mechanics, that that quantity is conserved.
In the energy representation used here, the condition is particularly simple: (6.1) shows that the matrix wmn must be diagonal, again in accordance with the usual matrix condition that a quantity is conserved in quantum mechanics, namely that the matrix of such a quantity can be brought to diagonal form simultaneously with the Hamiltonian.
As in § 3, we can now apply the results obtained to quasi-closed subsystems, for intervals of time during which they behave to a sufficient approximation as closed systems. Since the statistical distributions (or in this case the statistical matrices) of subsystems must be stationary, by the definition of statistical equilibrium, we first of all conclude that the matrices wmn are diagonal for all subsystems.† The problem of determining the statistical distribution therefore amounts to a calculation of the probabilities wn = wnn, which represent the “distribution function” in quantum statistics. Formula (5.4) for the mean value of any quantity f becomes simply
and contains only the diagonal matrix elements fnn.
Next, using the facts that w must be a quantum-mechanical integral of the motion and that the subsystems are quasi-independent, we find in a similar way to the derivation of (4.5) that the logarithm of the distribution function for subsystems must be of the form
where the index a corresponds to the various subsystems. Thus the probabilities wn can be expressed as a function of the energy level alone: wn = w(En).
Finally, the discussion in § 4 concerning the significance of additive integrals of the motion, and in particular the energy, as determining all the statistical properties of a closed system, remains entirely valid. This again enables us to set up for a closed system a simple distribution function suitable for describing its statistical properties though (as in the classical case) certainly not the true distribution function.
To formulate mathematically this “quantum microcanonical distribution” we must use the following device. The energy spectra of macroscopic bodies being “almost continuous”, we make use of the concept of the number of quantum states of a closed system which “belong” to a particular infinitesimal range of values of its energy.‡ We denote this number by dΓ; it plays a part analogous to that of the phase volume element dp dq in the classical case.
If we regard a closed system as consisting of subsystems, and neglect the interaction of the latter, every state of the whole system can be described by specifying the states of the individual subsystems, and the number dΓ is a product
of the numbers dΓa of the quantum states of the subsystems (such that the sum of the energies of the subsystems lies in the specified interval of energy of the whole system).
We can now formulate the microcanonical distribution analogously to the classical expression (4.6), writing
for the probability dw of finding the system in any of the dΓ states.
§ 7 Entropy
Let us consider a closed system for a period of time long compared with its relaxation time; this implies that the system is in complete statistical equilibrium.
The following discussion will be given first of all for quantum statistics. Let us divide the system into a large number of macroscopic parts (subsystems) and consider any one of them. Let wn be the distribution function for this subsystem; to simplify the formulae we shall at present omit from wn (and other quantities) the suffix indicating the subsystem. By means of the function wn we can, in particular, calculate the probability distribution of the various values of the energy E of the subsystem. We have seen that wn may be written as a function of the energy alone, wn = w(En). In order to obtain the probability W(E)dE that the subsystem has an energy between E and E+dE, we must multiply w(E) by the number of quantum states with energies in this interval; here we use the same idea of a “broadened” energy spectrum as was mentioned at the end of § 6. Let Γ(E) denote the number of quantum states with energies less than or equal to E. Then the required number of states with energy between E and E+dE can be written
and the energy probability distribution is
signifies geometrically that the area under the curve W = W(E) is unity.
In accordance with the general statements in § 1, the function W(E) has a very sharp maximum at E = Ē, being appreciably different from zero only in the immediate neighbourhood of this point. We may define the “width” ΔE of the curve W = W(E) as the width of a rectangle whose height is equal to the value of the function W(E) at the maximum and whose area is unity:
Using the expression (7.1), we can write this definition as
where
is the number of quantum states corresponding to the interval ΔE of energy. The quantity ΔΓ thus defined may be said to represent the “degree of broadening” of the macroscopic state of the subsystem with respect to its microscopic states. The interval ΔE is equal in order of magnitude to the mean fluctuation of energy of the subsystem.
These definitions can be immediately applied to classical statistics, except that the function w(E) must be replaced by the classical distribution function , and ΔΓ by the volume of the part of phase space defined by the formula
The phase volume Δp Δq, like ΔΓ, represents the size of the region of phase space in which the subsystem will almost always be found.
It is not difficult to establish the relation between ΔΓ in quantum theory and Δp Δq in the limit of classical theory. In the quasi-classical case, a correspondence can be set up between the volume of a region of phase space and the “corresponding” number of quantum states (see Quantum Mechanics, § 48): we can say that a “cell” of volume (2πħ)s (where s is the number of degrees of freedom of the system) “corresponds” in phase space to each quantum state. It is therefore clear that in the quasi-classical case the number of states ΔΓ may be written
where s is the number of degrees of freedom of the subsystem considered. This formula gives the required relation between ΔΓ and Δp Δq.
The quantity ΔΓ is called the statistical weight of the macroscopic state of the subsystem, and its logarithm
is called the entropy of the subsystem. In the case of classical statistics the corresponding expression is
The entropy thus defined is dimensionless, like the statistical weight itself. Since the number of states ΔΓ is not less than unity, the entropy cannot be negative. The concept of entropy is one of the most important in statistical physics.
It is apposite to mention that, if we adhere strictly to the standpoint of classical statistics, the concept of the “number of microscopic states” cannot be defined at all, and we should have to define the statistical weight simply as Δp Δq. But this quantity, like any volume in phase space, has the dimensions of the product of s momenta and s coordinates, i.e. the sth power of action ((erg·sec)s). The entropy, defined as log Δp Δq, would then have the peculiar dimensions of the logarithm of action. This means that the entropy would change by an additive constant when the unit of action changed: if the unit were changed by a factor a, Δp Δq would become as Δp Δq, and log Δp Δq would become log Δp Δq +s log a. In purely classical statistics, therefore, the entropy is defined only to within an additive constant which depends on the choice of units, and only differences of entropy, i.e. changes of entropy in a given process, are definite quantities independent of the choice of units.
This accounts for the appearance of the quantum constant ħ in the definition (7.8) of the entropy for classical statistics. Only the concept of the number of discrete quantum states, which necessarily involves a non-zero quantum constant, enables us to define a dimensionless statistical weight and so to give an unambiguous definition of the entropy.
We may write the definition of the entropy in another form, expressing it directly in terms of the distribution function. According to (6.4), the logarithm of the distribution function of a subsystem has the form
Since this expression is linear in En, the quantity
can be written as the mean value 〈log w(En)〉. The entropy S = log ΔΓ = = − log w(Ē) (from (7.3)) can therefore be written
i.e. the entropy can be defined as minus the mean logarithm of the distribution function of the subsystem. From the significance of the mean value,
this expression can be written in a general operator form independent of the choice of the set of wave functions with respect to which the statistical matrix elements are defined:†
Similarly, in classical statistics, the definition of the entropy can be written
Let us now return to the closed system as a whole, and let ΔΓ1, ΔΓ2, … be the statistical weights of its various subsystems. If each of the subsystems can be in one of ΔΓa quantum states, this gives
as the number of different states of the whole system. This is called the statistical weight of the closed system, and its logarithm is the entropy S of the system. Clearly
i.e. the entropy thus defined is additive: the entropy of a composite system is equal to the sum of the entropies of its parts.
For a clear understanding of the way in which entropy is defined, it is important to bear in mind the following point. The entropy of a closed system (whose total energy we denote by E0) in complete statistical equilibrium can also be defined directly, without dividing the system into subsystems. To do this, we imagine that the system considered is actually only a small part of a fictitious very large system (called in this connection a thermostat or heat bath). The thermostat is assumed to be in complete equilibrium, in such a way that the mean energy of the system considered (which is now a non-closed subsystem of the thermostat) is equal to its actual energy E0. Then we can formally assign to the system a distribution function of the same form as for any subsystem of it, and by means of this distribution determine its statistical weight ΔΓ, and therefore the entropy, directly from the same formulae (7.3)–(7.12) as were used for subsystems. It is clear that the presence of the thermostat has no effect on the statistical properties of individual small parts (subsystems) of the system considered, which in any case are not closed and are in equilibrium with the remaining parts of the system. The presence of the thermostat therefore does not alter the statistical weights ΔΓa of these parts, and the statistical weight defined in the way just described will be the same as that previously defined as the product (7.13).
So far we have assumed that the closed system is in complete statistical equilibrium. We must now generalise the above definitions to systems in arbitrary macroscopic states (partial equilibria).
Let us suppose that the system is in some state of partial equilibrium, and consider it over time intervals Δt which are small compared with the relaxation time for complete equilibrium. Then the entropy must be defined as follows. We imagine the system divided into parts so small that their respective relaxation times are small compared with the intervals Δt (remembering that the relaxation times in general decrease with decreasing size of the system). During the time Δt such parts may be regarded as being in their own particular equilibrium states, described by certain distribution functions. We can therefore apply to them the previous definition of the statistical weights ΔΓa, and so calculate their entropies Sa. The statistical weight ΔΓ of the whole system is then defined as the product (7.13), and the corresponding entropy S as the sum of the entropies Sa.
It should be emphasised, however, that the entropy of a non-equilibrium system, defined in this way as the sum of the entropies of its parts (satisfying the above condition), cannot now be calculated by means of the thermostat concept without dividing the system into parts. At the same time this definition is unambiguous in the sense that further division of the subsystems into even smaller parts does not alter the value of the entropy, since each subsystem is already in “complete” internal equilibrium.
In particular, attention should be drawn to the significance of time in the definition of entropy. The entropy is a quantity which describes the average properties of a body over some non-zero interval of time Δt. If Δt is given, to determine S we must imagine the body divided into parts so small that their relaxation times are small in comparison with Δt. Since these parts must also themselves be macroscopic, it is clear that when the intervals Δt are too short the concept of entropy becomes meaningless; in particular, we cannot speak of its instantaneous value.
Having thus given a complete definition of the entropy, let us now ascertain the most important properties and the fundamental physical significance of this quantity. To do so, we must make use of the microcanonical distribution, according to which a distribution function of the form (6.6) may be used to describe the statistical properties of a closed system:
Here dΓa may be taken as the differential of the function Γa(Ea), which represents the number of quantum states of a subsystem with energies less than or equal to Ea. We can write dw as
The statistical weight ΔΓa, by definition, is a function of the mean energy Ea of the subsystem; the same applies to Sa = Sa(Ēa). Let us now formally regard ΔΓa and Sa as functions of the actual energy Ea (the same functions as they really are of Ēa). Then we can replace the derivatives dΓa(Ea)/dEa in (7.15) by the ratios ΔΓa/ΔEa, where ΔΓa is a function of Ea in this sense, and ΔEa the interval of energy corresponding to ΔΓa (also a function of Ea). Finally, replacing ΔΓa by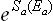 
, we obtain
where
is the entropy of the whole closed system, regarded as a function of the exact values of the energies of its parts. The factor eS, whose exponent is an additive quantity, is a very rapidly varying function of the energies Ea. In comparison with this function, the energy dependence of the quantity ΠΔEa is quite unimportant, and we can therefore replace (7.16) with very high accuracy by
But dw expressed in a form proportional to the product of all the differentials dEa is just the probability that all the subsystems have energies in given intervals between Ea and Ea + dEa. Thus we see that this probability is determined by the entropy of the system as a function of the energies of the subsystems; the factor δ(E−E0) ensures that the sum E = ΣEa has the given value E0 of the energy of the system. This property of the entropy, as we shall see later, is the basis of its applications in statistical physics.
We know that the most probable values of the energies Ea are their mean values Ēa. This means that the function S(E1, E2, …) must have its maximum possible value (for a given value of the sum ΣEa = E0) when Ea = Ēa. But the Ēa are just the values of the energies of the subsystems which correspond to complete statistical equilibrium of the system. Thus we reach the important conclusion that the entropy of a closed system in a state of complete statistical equilibrium has its greatest possible value (for a given energy of the system).
Finally, we may mention another interesting interpretation of the function S = S(E), the entropy of any subsystem or closed system; in the latter case it is assumed that the system is in complete equilibrium, so that its entropy may be expressed as a function of its total energy alone. The statistical weight ΔΓ = eS(E) by definition, is the number of energy levels in the interval ΔE which describes in a certain way the width of the energy probability distribution. Dividing ΔE by ΔΓ, we obtain the mean separation between adjoining levels in this interval (near the energy E) of the energy spectrum of the system considered. Denoting this distance by D(E), we can write
Thus the function S(E) determines the density of levels in the energy spectrum of a macroscopic system. Since the entropy is additive, we can say that the mean separations between the levels of a macroscopic body decrease exponentially with increasing size of the body (i.e. with increasing number of particles in it).
§ 8 The law of increase of entropy
If a closed system is not in a state of statistical equilibrium, its macroscopic state will vary in time, until ultimately the system reaches a state of complete equilibrium. If each macroscopic state of the system is described by the distribution of energy between the various subsystems, we can say that the sequence of states successively traversed by the system corresponds to more and more probable distributions of energy. This increase in probability is in general very considerable, because it is exponential, as shown in § 7. We have seen that the probability is given by eS, the exponent being an additive quantity, the entropy of the system. We can therefore say that the processes occurring in a non-equilibrium closed system do so in such a way that the system continually passes from states of lower to those of higher entropy until finally the entropy reaches the maximum possible value, corresponding to complete statistical equilibrium.
Thus, if a closed system is at some instant in a non-equilibrium macroscopic state, the most probable consequence at later instants is a steady increase in the entropy of the system. This is the law of increase of entropy or second law of thermodynamics, discovered by R. Clausius (1865); its statistical explanation was given by L. Boltzmann in the 1870s.
In speaking of the “most probable” consequence, we must remember that in reality the probability of transition to states of higher entropy is so enormous in comparison with that of any appreciable decrease in entropy that in practice the latter can never be observed in Nature. Ignoring decreases in entropy due to negligible fluctuations, we can therefore formulate the law of increase of entropy as follows: if at some instant the entropy of a closed system does not have its maximum value, then at subsequent instants the entropy will not decrease; it will increase or at least remain constant.
There is no doubt that the foregoing simple formulations accord with reality; they are confirmed by all our everyday observations. But when we consider more closely the problem of the physical nature and origin of these laws of behaviour, substantial difficulties arise, which to some extent have not yet been overcome.
Firstly, if we attempt to apply statistical physics to the entire Universe, regarded as a single closed system, we immediately encounter a glaring contradiction between theory and experiment. According to the results of statistics, the universe ought to be in a state of complete statistical equilibrium. More precisely, any finite region of it, however large, should have a finite relaxation time and should be in equilibrium. Everyday experience shows us, however, that the properties of Nature bear no resemblance to those of an equilibrium system; and astronomical results show that the same is true throughout the vast region of the Universe accessible to our observation.
The escape from this contradiction is to be sought in the general theory of relativity. The reason is that, when large regions of the Universe are considered, the gravitational fields present become important. These fields are just a change in the space-time metric. When the statistical properties of bodies are discussed, the metric properties of space-time may in a sense be regarded as “external conditions” to which the bodies are subject. The statement that a closed system must, over a sufficiently long time, reach a state of equilibrium, applies of course only to a system in steady external conditions. On the other hand, the general cosmological expansion of the Universe means that its metric depends essentially on time, so that the “external conditions” are by no means steady in this case. Here it is important that the gravitational field cannot itself be included in a closed system, since the conservation laws which are, as we have seen, the foundation of statistical physics would then reduce to identities. For this reason, in the general theory of relativity, the Universe as a whole must be regarded not as a closed system but as a system in a variable gravitational field. Consequently the application of the law of increase of entropy does not prove that statistical equilibrium must necessarily exist.
Thus this aspect of the problem of the Universe as a whole indicates the physical basis of the apparent contradictions. There are, however, other difficulties in understanding the physical nature of the law of increase of entropy.
Classical mechanics itself is entirely symmetrical with respect to the two directions of time. The equations of mechanics remain unaltered when the time t is replaced by – t; if these equations allow any particular motion, they will therefore allow the reverse motion, in which the mechanical system passes through the same configurations in the reverse order. This symmetry must naturally be preserved in a statistics based on classical mechanics. Hence, if any particular process is possible which is accompanied by an increase in the entropy of a closed macroscopic system, the reverse process must also be possible, in which the entropy of the system decreases. The formulation of the law of increase of entropy given above does not itself contradict this symmetry, since it refers only to the most probable consequence of a macroscopically described state. In other words, if some non-equilibrium macroscopic state is given, the law of increase of entropy asserts only that, out of all the microscopic states which meet the given macroscopic description, the great majority lead to an increase of entropy at subsequent instants.
A contradiction arises, however, if we look at another aspect of the problem. In formulating the law of increase of entropy, we have referred to the most probable consequence of a macroscopic state given at some instant. But this state must itself have resulted from some other states by means of processes occurring in Nature. The symmetry with respect to the two directions of time means that, in any macroscopic state arbitrarily selected at some instant t = t0, we can say not only that much the most probable consequence at t > t0 is an increase in entropy, but also that much the most probable origin of the state was from states of greater entropy; that is, the presence of a minimum of entropy as a function of time at the arbitrarily chosen instant t = t0 is much the most probable.†
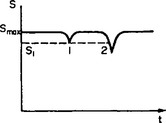
FIG. 1
This assertion, of course, is not at all equivalent to the law of increase of entropy, according to which the entropy never decreases (apart from entirely negligible fluctuations) in any closed systems which actually occur in Nature. And it is precisely this general formulation of the law of increase of entropy which is confirmed by all natural phenomena. It must be emphasised that it is certainly not equivalent to the formulation given at the beginning of this section, as it might appear to be. In order to derive one formulation from the other, it would be necessary to use the concept of an observer who artificially “creates” a closed system at some instant, so that the problem of its previous behaviour does not arise. Such a dependence of the laws of physics on the nature of an observer is quite inadmissible, of course.
It is doubtful whether the law of increase of entropy thus formulated could be derived on the basis of classical mechanics. Moreover, because of the invariance of the equations of classical mechanics under time reversal, one could seek only to derive a monotonic variation of entropy. In order to obtain a law of monotonic increase, we should have to define the direction of time as that in which the entropy increases. The problem would then arise of proving that such a thermodynamic definition was identical with the quantum-mechanical definition (see below).
In quantum mechanics, the situation is substantially changed. The fundamental equation of quantum mechanics, namely Schrödinger’s equation, is itself symmetrical under time reversal, provided that the wave function Ψ is also replaced by Ψ*. This means that, if at some instant t = t1 the wave function Ψ = Ψ(t1) is given, and if according to Schrödinger’s equation it should become Ψ(t2) at some other instant t2, then the change from Ψ(t1) to Ψ(t2) is reversible; in other words, if Ψ = Ψ*(t2) at the initial instant t1, then Ψ = Ψ*(t1) at t2.
However, despite this symmetry, quantum mechanics does in fact involve an important non-equivalence of the two directions of time. This appears in connection with the interaction of a quantum object with a system which with sufficient accuracy obeys the laws of classical mechanics, a process of fundamental significance in quantum mechanics. If two interactions A and B with a given quantum object occur in succession, then the statement that the probability of any particular result of process B is determined by the result of process A can be valid only if process A occurred earlier than process B; see also Quantum Mechanics, § 7.
Thus in quantum mechanics there is a physical non-equivalence of the two directions of time, and theoretically the law of increase of entropy might be its macroscopic expression. In that case, there must exist an inequality involving the quantum constant ħ which ensures the validity of this law and is satisfied in the real world. Up to the present, however, no such relation has been at all convincingly shown to exist.
The question of the physical foundations of the law of monotonic increase of entropy thus remains open: it may be of cosmological origin and related to the general problem of initial conditions in cosmology; the violation of symmetry under time reversal in some weak interactions between elementary particles may play some part. The answers to such questions may be achieved only in the course of further synthesis of physical theories.
Summarising, we may repeat the general formulation of the law of increase of entropy: in all closed systems which occur in Nature, the entropy never decreases; it increases, or at least remains constant. In accordance with these two possibilities, all processes involving macroscopic bodies are customarily divided into irreversible and reversible processes. The former comprise those which are accompanied by an increase of entropy of the whole closed system; the reverse processes cannot occur, since the entropy would then have to decrease. Reversible processes are those in which the entropy of the closed system remains constant,† and which can therefore take place in the reverse direction. A strictly reversible process is, of course, an ideal limiting case; processes actually occurring in Nature can be reversible only to within a certain degree of approximation.
†For brevity, we shall usually say, as is customary, that the system “is in the volume Δp Δq of phase space”, meaning that the system is in states represented by phase points in that volume.
‡In what follows we shall always use the conventional notation dp and dq to denote the products of the differentials of all the momenta and all the coordinates of the system respectively.
†In this book we shall denote averaging by a bar over the symbol or by angle brackets: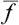 
or 〈f〉, being influenced in this solely by convenience in writing the formulae. The second way is preferable for writing the mean values of lengthy expressions.
†We may give an example to illustrate the very high degree of accuracy with which this is true. If we consider a region in a gas which contains, say, only 1/100 gram-molecule, we find that the mean relative variation of the energy of this quantity of matter from its mean value is only ˜ 10−11. The probability of finding (in a single observation) a relative deviation of the order of 10−6, say, is given by a fantastically small number, ˜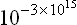 
†Provided, of course, that these subsystems together still form only a small part of the whole closed system.
†Such an imaginary set of identical systems is usually called a statistical ensemble.
†The definition and properties of the delta function are given, for example, in Quantum Mechanics, § 5.
‡It should be emphasised once more that this distribution is not the true statistical distribution for a closed system. Regarding it as the true distribution is equivalent to asserting that, in the course of a sufficiently long time, the phase trajectory of a closed system passes arbitrarily close to every point of the manifold defined by equations (4.3). But this assertion (called the ergodic hypothesis) is certainly not true in general.
†The separations between successive energy levels of a single particle are inversely proportional to the square of the linear dimensions L of the volume enclosing it (˜ ħ2/mL2, where m is the mass of the particle and ħ the quantum constant).
†It should be mentioned that this discussion is inapplicable to the initial part of the energy spectrum; the separations between the first few energy levels of a macroscopic body may even be independent of the size of the body. This point, however, does not affect the subsequent conclusions: when referred to a single particle, the separations between the first few levels for a macroscopic body are negligibly small, and the high density of levels mentioned in the text is reached for very small values of the energy relative to a single particle.
†The energy representation is mentioned here, as being the one generally used in statistical physics. We have not so far, however, made direct use of the fact that the Ψn are wave functions of stationary states. It is therefore clear that the same method could be used to define the density matrix with respect to any complete set of wave functions.
The usual coordinate density matrix (q, q’) (see Quantum Mechanics, § 14) is expressed in terms of the matrix wmn by
†The functions Ψp(q) are plane waves in the configuration space of the system; they are assumed normalised by the delta function of all the momenta.
‡Since I(q, p) has no direct physical significance, the definition of the function with the properties stated is of course not unique. For example, the q and p distributions can be obtained by the same method from the function
where ξ denotes the set of auxiliary variables ξ1,…, ξs, and dξ = dξ1 … dξs (E. P. Wigner, 1932): since
the integral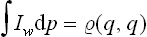 
. The integral ∫ IWdq, after the change of variables 
, is the same as ∫ I dq. Unlike I(q, p), IW(q, p) is real (as can be easily seen by using the fact that the matrix (q, q’) is Hermitian), but in general it is not everywhere positive.
†In § 5 the density matrix of a subsystem was discussed, having regard to its fundamental applications in statistical physics, but a density matrix can of course also be used to describe a closed system in a mixed state.
†Since this statement involves neglecting the interactions between subsystems, it is more precise to say that the non-diagonal elements wmn tend to zero as the relative importance of these interactions decreases, and therefore as the number of particles in the subsystems increases.
‡It will be remembered that in § 4 we agreed to ignore entirely the momentum and angular momentum of the system as a whole, for which purpose it is sufficient to consider a system enclosed in a rigid “box” with coordinates such that the box is at rest.
†In accordance with the general rules, the operator log must be understood as an operator whose eigenvalues are equal to the logarithms of the eigenvalues of the operator , and whose eigenfunctions are the same as those of .
†For a better understanding of this symmetry, we may plot diagrammatically the variation of the entropy of a system that is closed during a very long interval of time (Fig. 1). Let a macroscopic state with entropy S = S1 < Smax be observed in such a system, arising from a (very improbable) large fluctuation. Then we can say that it will be, with very high probability, a point of type 1, at which the entropy has reached a minimum, and not one of type 2, at which the entropy will decrease further.
†It must be emphasised that the entropies of the individual parts of the system need not remain constant also.