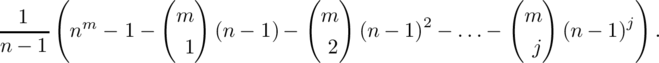1 n − 1 ( n m − 1 − ( m 1 ) ( n − 1 ) − ( m 2 ) ( n − 1 ) 2 − … − ( m j ) ( n − 1 ) j ) .

They also proved that the m-dimensional versions of both Euler’s and MacNeish’s conjectures (see Section 5.1 and Section 5.3) are false for m > 2 whenever they are false for m = 2.

The significance of latin cubes and hypercubes is more easily understood if we regard them as special cases of another design which arises by generalizing the concept of a set of orthogonal latin squares in a different way.

Let L ₁, L ₂,…, L_{k −2} be a set of k − 2 MOLS of order n whose elements are the integers 1, 2,…, n and let a k × n ² matrix M be formed in the following way. The first row of M has as its elements the integer 1 repeated n times, the integer 2 repeated n times, and so on until finally the integer n is repeated n times. The second row of M comprises the sequence of integers 1, 2, …, n repeated n times. If 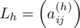L h = ( a ij ( h ) ) , the (h + 2)-th row of M has 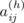a ij ( h ) as the entry in the [(i − 1)n + j]-th column: namely, the column whose first two entries are i and j. A simple example is given in Figure 5.6.6. In general, the matrix M so constructed has the property that each ordered pair of elements appears just once as a column in any two-rowed submatrix by virtue of the facts that the squares L ₁, L ₂, …, L_{k −2} are all latin and are also pairwise orthogonal. We say that it is an orthogonal array of k constraints and n levels having strength 2 and index 1. (See also Section 11.1.) More generally, we may make the following definition.

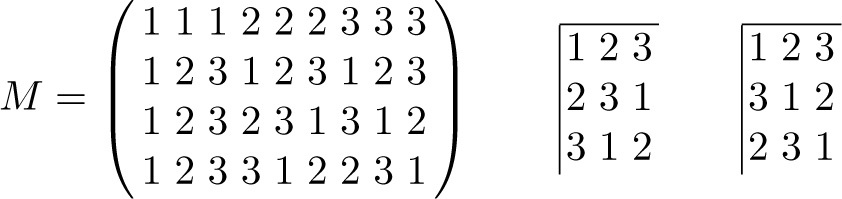
Fig. 5.6.6

Definition

An orthogonal array of size N with k constraints, n levels, strength t and index λ is a k × N matrix M having n different elements and with the property that each different ordered t-tuple of elements occurs exactly λ times as a column in any t-rowed submatrix of M.

It is immediate from the definition that N = λn^t . It is also clear from the construction given above that any orthogonal array of k constraints, n levels, strength 2 and index 1 is equivalent to a set of k − 2 MOLS of order n. We shall defer a formal proof of this fact until Section 11.1. From Theorem 5.1.2, we may deduce that, if M is an orthogonal array with t = 2 and λ = 1 then k ≤ n+1. [See also Rao(1949).] The investigation of upper bounds for the number of constraints in other cases has been the subject of numerous papers. See, in particular, Rao(1946,1947), Bose and Bush(1952), Bush(1952a,b) and Seiden and Zemach(1966). Also, we refer the reader to a more recent monograph by Hedayat, Sloane and Stufken(1999), and to the bibliography therein, for a fairly comprehensive treatment of the subject which, however, puts its main emphasis on the application to coding and to statistical design of experiments.

The connection between these orthogonal arrays and latin cubes and hypercubes is given by the statements: (i) a latin cube of order n is equivalent to an orthogonal array of 4 constraints and n levels having strength 2 and index n; (ii) a set of k − 3 mutually orthogonal latin cubes of order n is equivalent to an orthogonal array of k constraints and n levels having strength 2 and index n; (iii) a set of k − m mutually orthogonal m-dimensional latin hypercubes of order n is equivalent to an orthogonal array of k constraints and n levels having strength 2 and index n^{m −2}.

As an illustration of statement (ii), we give in Figure 5.6.7 the orthogonal array M corresponding to the two orthogonal latin cubes shown in Figure 5.6.3. Here the first, second and third rows of M give the row, column and file respectively of the cell of the latin cube whose entry appears below them in the fourth or fifth row of M according to which of the two latin cubes is being considered.

Fig. 5.6.7

Plackett and Burman(1943-1946) proved that the maximum number of constraints k for an orthogonal array of n levels having strength 2 and index λ satisfies the inequality k ≤ (λn ² − 1)/(n − 1). An alternative proof of the same result was later given by Bose and Bush(1952). If we put λ = n, we get k ≤ n ² + n + 1 for this case and it follows that the maximum number of latin cubes in a pairwise orthogonal set is n ² + n − 2, as stated earlier.

---

¹ The descriptive term orthogonal mate for a latin square L ₂ which is orthogonal to a given latin square L ₁ was first used by Parker(1963).

² An interesting alternative proof of this theorem is in Liang(201?).

³ For a generalization of the problem of the 36 officers, see Rao(1961).

⁴ In Bose and Shrikhande(1960), the original counter-example for n = 22 was generalized to give pairs of MOLS of all orders n of the form 36m + 22.

⁵ The ambiguity in this choice is one reason why a projective plane may possibly define more than one set of MOLS up to equivalence. See below for the definition of equivalence.

⁶ We call two lines parallel if they have no finite point in common.

⁷ For more details, see below.

⁸ See Section 11.2 for more details.

⁹ Todorov’s result that N(14) ≥ 3 was not known at the time Wallis wrote his paper.

¹⁰ That is, the elements along each of the main diagonals are all different. For more information about such squares, see the next chapter.

¹¹ There are many such orderings, one for each choice of the element u_w .

¹² We define Room squares and explain O’Shaughnessy’s construction in Section 6.4.

¹³ See Section 2.1 for an earlier discussion of notation for parastrophes.

¹⁴ If A(u, v) = w, then A^r (u, w) = v and so A^rl (v, w) = u. Thus, A^rl (x, y) = z ⇒ A(z, x) = y.

¹⁵ It is interesting to compare this result with Brouwer’s construction of four almost-orthogonal 10 × 10 latin squares mentioned on pages 147, 149 and elsewhere in [DK2].

¹⁶ A quite different definition of orthogonality for permutation cubes has been introduced in Höhler(1970) and yet another in Warrington(1973).