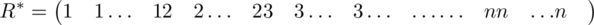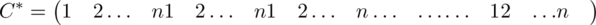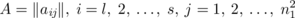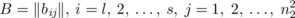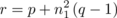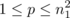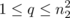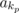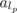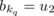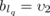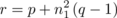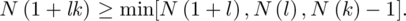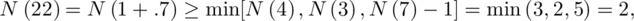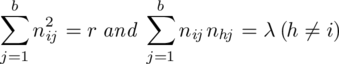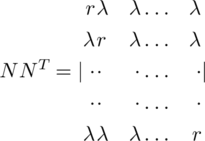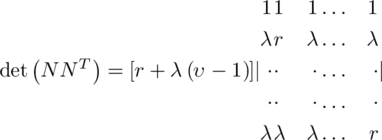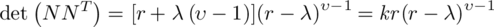Miscellaneous topics
The first two sections of this final chapter are devoted to the important subjects of orthogonal arrays and direct products, both of which can be used to construct sets of orthogonal latin squares of larger order from ones of smaller orders. In the third section of the chapter, we explain the Kézdy-Snevily conjecture and the fact that its truth would imply the truth of both Brualdi’s and Ryser’s conjectures. In the fourth section, we introduce the relatively new concept of the chromatic number of a latin square. The next topics considered are the practical applications of latin squares to coding, experimental designs and games tournaments. Lastly, we introduce latin triangles and also we comment on the use of computers in the solution of latin square problems.
11.1 Orthogonal arrays and latin squares
We mentioned in Section 5.6 that a set of h − 2 orthogonal latin squares is equivalent to the existence of a particular type of orthogonal array. Our main task in the present section is to confirm the validity of the last result by formally demonstrating the equivalence between a set of h − 2 mutually orthogonal latin squares of order n and an orthogonal array of h rows (or constraints), n 2 columns (n levels), strength 2, and index unity.
We shall begin with a definition.
For example, the two n × n matrices R and C given in Figure 11.1.1 are clearly n 2-orthogonal.
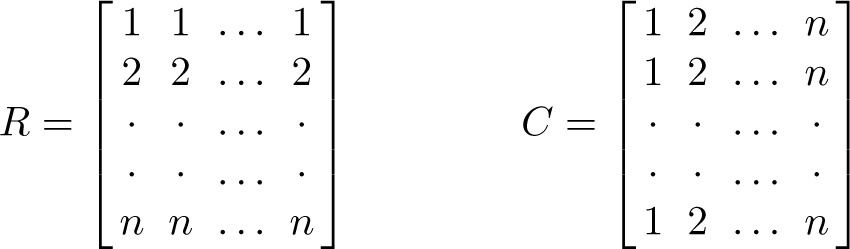
Fig. 11.1.1
Likewise, the two 1 × n 2 matrices
and
obtained from R and C respectively by writing their rows consecutively are n 2-orthogonal. Evidently, two n 2-orthogonal n × n matrices which are such that each of 1, 2,…, n occurs exactly once in each row and once in each column are orthogonal latin squares.
As an example, we shall outline the construction of a pair of orthogonal latin squares of order 15 (or equivalently, an OA(15, 4)) from the pairs of orthogonal latin squares of orders 3 and 5 given in Figure 11.1.2, using the method given in our proof above.
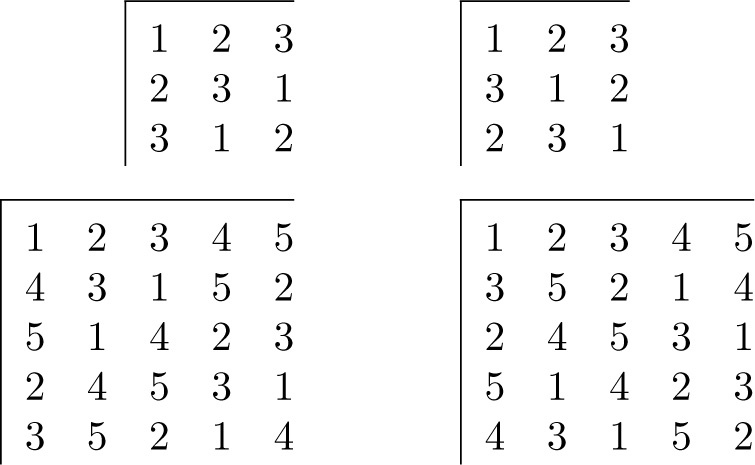
Fig. 11.1.2
We first form sets of four 32-orthogonal 3 × 3 matrices and 52-orthogonal 5 × 5 matrices by appending the matrices R and C of appropriate size to the squares given. Then, writing the rows of each matrix in a single row, we get an OA(3, 4) and an OA(5, 4) as in Figure 11.1.3.

Fig. 11.1.3
From these, we derive an OA(15, 4) of 255 columns, and, of these columns, we exhibit only the 1st to the 18th and the 37th to 54th in Figure 11.1.4.

Fig. 11.1.4
We reorder these 225 columns in such a way that the first two rows of the matrix represent the rows, written consecutively, of two 15 × 15 matrices R and Cand the remaining two rows then represent, in order, the rows of the two desired orthogonal latin squares of order 15. Hence the latter can be written down.
The result stated in Theorem 11.1.2 has probably been more used than any other in constructions of sets of MOLS. In particular, it leads at once to a property of the function N(n) which was first pointed out by MacNeish(1922): namely,
The theorem asserts that there exist at least
 MOLS of order
MOLS of order
 . Since we know by Theorem 5.2.3 that there are at least
. Since we know by Theorem 5.2.3 that there are at least
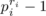 MOLS of order
MOLS of order
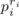 for each i, i = 1, 2, …, r, the result follows by repeated application of the corollary to Theorem 11.1.2. For an alternative proof, see Section 11.2.
for each i, i = 1, 2, …, r, the result follows by repeated application of the corollary to Theorem 11.1.2. For an alternative proof, see Section 11.2.
MacNeish’s theorem gives a lower bound for N(n). As already mentioned in Section 5.3, MacNeish himself conjectured that this was also an upper bound because, for example, this is certainly the case when n itself is a prime power. Further evidence for this conjecture seemed to have been provided when, some twenty years later, Mann(1942) proved Theorem 7.2.2.
The MacNeish conjecture was not disproved until 1959 when Parker showed (as a counter-example) that there exists a set of at least four mutually orthogonal latin squares of order 21. See Section 5.3 for the further history of this topic.
We end this brief section by mentioning that J.W.Brown(1972) has used the medium of orthogonal arrays to describe an extension of Theorem 5.1.6 to the special case of a triple of MOLS of order ten.
For a survey of recursive and other constructions of orthogonal latin squares used up to the date of publication of that paper, see Colbourn and Dinitz(2001).
11.2 The direct product and singular direct product of quasigroups
A much-used means of obtaining pairs (or larger sets) of orthogonal latin squares from given sets of MOLS of smaller orders is by constructing the direct product or generalized direct product of the quasigroups which are defined by the squares of the given orders. We have already mentioned this approach earlier in this book. For example, MacNeish’s theorem (Section 5.3 andSection 11.1) may be translated into the language of quasigroups by means of the concept of direct product.
We have the following theorem:
If G has n
1 elements and H has n
2 elements, then F has n
1
n
2 elements. If there exist N(n) mutually orthogonal latin squares of order n, then there exist N(n) mutually orthogonal quasigroups of that order. Hence, by forming the direct products of min[N(n
1), N(n
2)] pairs of quasigroups of orders n
1 and n
2 (those of the same order n
1 or n
2 being orthogonal), we can obtain an equal number of mutually orthogonal quasigroups of order n
1
n
2. Thus, N(n) ≥ min[N(n
1), N(n
2)], as we obtained in Section 11.1 by an argument in terms of orthogonal arrays. In particular, if
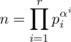 where the pi
are distinct primes, we have
where the pi
are distinct primes, we have
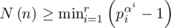 , which is MacNeish’s theorem.
, which is MacNeish’s theorem.
By use of a generalized form of the above direct product method which he called “produit direct singulier”, Sade has shown how a latin square of order m + lk may be constructed from given latin squares Lg , Lr and Lh , where Lg is a latin square of order m + l which contains a latin subsquare of order m and Lr , Lh have orders l, k respectively. Taking advantage of the fact that the direct product of two (or more) pairs of orthogonal quasigroups is again a pair of orthogonal quasigroups, as proved above, he has thence been able to obtain sets of orthogonal latin squares of order m + lk in cases when the values of the integers m, l, k are suitable. In particular, the method provides counter-examples to the Euler conjecture. For the details, see Sade(1960a). We shall give only a summary of Sade’s results.
Let (G, ·) be a quasigroup of order n = m + l which contains a subquasigroup (Q, ·) of order m and let (R, ⊗) be a quasigroup of order l defined on the set R = G − Q. Let (H, ⊕) be an idempotent quasigroup of order k. The set T = Q ∪ (R × H) is then of order m + lk and we define an operation (ο) on it in such a way that the structure (T, ο) is a quasigroup, called by Sade the singular direct product of the four given quasigroups. [Note that T consists of elements qu ∈ Q and ordered pairs (rυ , hw ) ∈ (R × H).]
The operation (ο) is defined by the following five statements:
- (i) for all q 1, q 2 ∈ Q, q 1 ο q 2 = q 1 q 2;
- (ii) for all q ∈ Q, r ∈ R, h ∈ H, q ο (r, h) = (qr, h) and (r, h) ο q = (rq, h);
- (iii) for r 1, r 2 ∈ R, h 1, h 2 ∈ H, h 1 ≠ h 2, (r 1, h 1) ο (r 2, h 2) = (r 1 ⊗ r 2, h 1 ⊕ h 2);
- (iv) for r 1, r 2 ∈ R with r 1 r 2 ∈ R, and for h ∈ H (r 1, h) ο (r 2, h) = (r 1 r 2, h);
- (v) for r 1, r 2 ∈ R with r 1 r 2 ∈ Q, and for h ∈ H, (r 1, h) ο (r 2, h) = r 1 r 2.
By way of explanation of these definitions, let us remark firstly that, whereas r 1 ⊗ r 2 ∈ R for all choices of r 1, r 2 ∈ R, we cannot make the same statement about the products r 1 r 2. We have r 1 r 2 ∈ G but, in general, some of the products will be in Q. However, as may clearly be seen from Figure 11.2.1, we always have qr ∈ R and rq ∈ R whatever the choices of q ∈ Q and r ∈ R: for, since Q is a quasigroup and since each element of Q is to occur exactly once in each row and each column of the multiplication table of G, no element of Q can occur in either of the subsquares A or B shown in Figure 11.2.1. Again from Figure 11.2.1, we see that the ordered pairs (qri , h) and (rri , h) for values of r such that rri ∈ R just cover the set R × {h} as q and r vary through the sets Q and R respectively with ri ∈ R kept fixed. [We have qri ∉ Q for all q ∈ Q. But gri for g ∈ G covers G, so the products qri (with q ∈ Q) together with the products rri for which rri ∉ Q together cover G − Q = R.] The same is true of the ordered pairs (riq, h) and (rir, h).
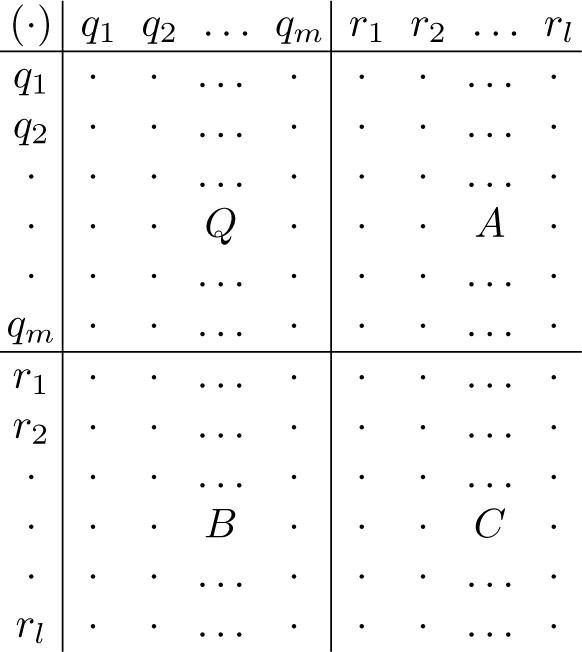
Fig. 11.2.1
We are now able to prove, as in Sade(1960a),
The proofs of both the theorems just stated involve consideration of many cases and Sade does not give detailed proofs. From them, we may deduce the following one.
By putting m = 1 in the above theorem, we may deduce that
It follows that
so there exist at least two orthogonal latin squares of order 22 which is a counter-example to Euler’s conjecture. (See Section 5.1.)
Lindner has made use of the singular direct product to obtain a number of interesting results, and he has also generalized the construction in several ways. In his earliest paper on the subject, Lindner(1971d), he has proved that the singular direct product preserves the Stein identity x(xy) = yx [identity (11) of Section 2.1]. As was pointed out on page 184, quasigroups which satisfy the Stein identity (called Stein quasigroups) are orthogonal to their own transposes (that is, they are anti-abelian) and, using this fact, Lindner has constructed several new classes of quasigroups having this property. In Lindner(1971g,1972a,b), he has investigated the general question of what kinds of quasigroup identity are preserved by the singular direct product. In two further papers, Lindner(1971e,f), he has generalized the singular direct product in two different ways. For more details, see [DK1] or the original papers. In another paper, Lindner(1971c), he has used a third generalization of the singular direct product which combines the two generalizations just mentioned to construct a large number of latin squares each of which is orthogonal to a given latin square L and no two of which are isomorphic.
Yamamoto’s construction, mentioned on page 287, may also be regarded as a generalized direct product.
Versions of the singular direct product have been used for (i) constructing pairs of perpendicular Steiner quasigroups [Lindner and N.S.Mendelsohn(1973)]; (ii) constructing so-called self-orthogonal latin squares (see Section 5.5) [Crampin and Hilton(1975a,b)]; (iii) constructing sets of orthogonal diagonal latin squares (see Section 6.1) [Lindner(1973), Crampin and Hilton(1975b), Hilton(1975b,c), Heinrich and Hilton(1983)]; (iv) constructing skew Room squares [Mullin(1980)].
In more recent years, analogues of the singular direct product have been derived for Steiner triple systems [Ling, Colbourn, Grannell and Griggs(2000), Dinitz and Stinson(2002)] and Steiner quadruple systems [Hartman(1981), Ji and Zhu(2003)]. Also, quite recently Liang(201?) has extended the original singular direct product construction of Sade to make it apply to standardized quasi-orthogonal latin squares.
11.3 The Kézdy-Snevily conjecture
A conjecture (which we shall call the K-S conjecture, see below) concerning covering of the elements of a metric space by spheres would, if true, prove both the conjecture that every latin square of odd order has a transversal (attributed to Ryser) and the conjecture that every latin square of order n has a partial transversal of length at least n − 1 (attributed to Brualdi).
Let Sn denote the symmetric group formed by the n! permutations of n elements, say 1, 2, …, n. Regard these as the vertices of a metric space where the distance between any two permutations is their Hamming distance: that is, the number of places in which they differ.
If a subset T of permutations of Sn is given, its covering radius cr(T) is the smallest r such that Sn is covered by the spheres of radius r whose centres are the permutations of T.
Suppose that T is a sharply transitive subset of permutations of Sn . Then |T| = n since exactly one member of T maps a selected integer i to the integer j for each j ∈ {1, 2, …, n}. The permutations which define the rows of a latin square L as re-arrangements from natural order form such a subset T and, conversely, every such sharply transitive subset defines a latin square L.
Suppose further that ρ ∈ Sn has distance n − 1 from every member of T. Then, for each i ∈ {1, 2, …, n}, there is exactly one member τ ∈ T such that iτ = iρ = k say, because τ and ρ agree in only one place. Also, because T is sharply transitive, i is different for each τ ∈ T. Each i defines a column of L and each k defines an entry in that column. These entries form a transversal of L because they are all different and are in different rows and columns of L.
Example. In Figure 11.3.1, let the permutations which define the rows of L be denoted by τh for h = 1, 2, 3, 4. Each of the permutations ρ and ρ′ has distance three from the permutations of T and defines a transversal of L of which the elements are indicated by suffices a and b respectively.
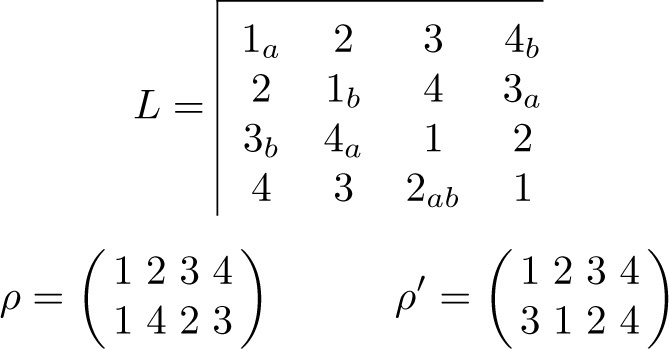
Fig. 11.3.1
In Cameron and Wanless(2005), the following theorem is proved.
Let f(n, s) denote the smallest cardinal for which there is a subset T of permutations of Sn such that the spheres with centres at the members of T and radius n − s cover Sn . For example, f(n, n) = n! since each sphere of zero radius covers only the permutation which is its centre. Because each two permutations of Sn differ in at least two places, each sphere of radius one likewise covers only the permutation which is its centre, so we also have f(n, n − 1) = n!. Since any permutation of Sn differs in at most n places from a given permutation ρ, a single sphere of radius n and centre at ρ covers Sn : that is, f(n, 0) = 1.
Cameron and Wanless(2005) have shown that f(n, 1) = ⌊n/2⌋ + 1 though they attribute this result to A.E. Kézdy and H.S. Snevily. The value of f(n, 2) is not known but the authors just mentioned have conjectured that f(n, 2) > n if n is odd and f(n, 2) = n if n is even. For more information about this function and the Kézdy-Snevily conjecture, see Cameron and Wanless(2005) and Wanless and Zhang(2013).
Suppose that the conjecture f(n, 2) > n when n is odd turns out to be true. Then, for every set of n spheres of radius n − 2 in the metric space Sn , there is at least one permutation ρ which is uncovered. So ρ has distance n − 1 or greater from the centres of all the spheres. In the case when the centres of the spheres are the permutations which define the rows of a latin square L, they form a sharply transitive set T and so no permutation has distance more than n − 1 from any one of them. So there exists a permutation ρ whose distance is exactly n − 1 from each of the n permutations of L. Hence, ρ defines a transversal of L. Thus, validity of the K-S conjecture when n is odd would prove Ryser’s conjecture.
Validity of the same conjecture would also prove Brualdi’s conjecture.
To see this, consider the following two examples.
In the first example (Figure 11.3.2), the latin square shown has a partial transversal (indicated by the entries with suffix a) of length five which cannot be extended. The missing entry u in the permutation ρ is necessarily 1 and so ρ intersects the second row of L twice (2 → 3, 6 → 1) and the last row not at all.

Fig. 11.3.2
In the second example (Figure 11.3.3), the latin square shown has a partial transversal (indicated by the entries with suffix b) of length four which cannot be extended. The missing entries u and υ in the permutation ρ are necessarily 1 and 2 and so ρ intersects the third and sixth rows of L twice if u =1 and υ = 2 (2 → 1, 3 → 2) or the first and second rows twice if u = 2 and υ = 1 (2 → 2, 3 → 1) and the remaining rows not at all. Clearly, there may also be examples in which ρ intersects one row thrice and another not at all.

Fig. 11.3.3
We return to our proof.
Let us now append an additional symbol, say the symbol n + 1, to each of the rows of L to give an n × (n + 1) rectangle L′ whose rows may be regarded as forming a set T′ of cardinal n of permutations of Sn +1. We shall show that every permutation σ′ ∈ Sn +1 intersects at least one member of T′ twice (or more) and so has distance at most (n + 1) − 2 = n − 1 from some member of T′.
Suppose that the conjecture f(n + 1, 2) ≥ n + 1 (for n either odd or even) is true. Then there is no subset T* of permutations of Sn +1 of cardinal n such that the spheres with centres at the permutations of T* and radius (n + 1) − 2 cover Sn +1. But this contradicts the fact (about to be proved) that every permutation σ′ ∈ Sn +1 has distance at most n − 1 from some member of T′. Consequently, no latin square of order n has a partial transversal which cannot be extended to one of n − 1 cells.
If (n + 1)σ′ = n + 1, then certainly σ′ intersects some member of T′ twice since every permutation of Sn intersects some row of L at least once (in view of the fact that the rows of L form a sharply transitive subset of Sn ). Suppose therefore that (n + 1)σ′ = s < n + 1 and that tσ′ = n + 1. Let σ be the permutation of Sn such that wσ = wσ′ for all w ≠ t and tσ = s.
If σ intersects some row of L in three or more places, then σ′ intersects some row of L′ in two or more places as we wished to prove. If not, then σ intersects each of two rows of L (say the rows r 1 and r 2 represented by the permutations ρ 1 and ρ 2) in two places. But tρi = s for at most one of i = 1, 2, say i = 2. Then σ′ intersects the row r 1 of L′ in two places, which completes the proof.
Remark concerning the first example for the KS-conjecture.
Since any permutation which intersects a particular row just once defines a partial transversal which includes the entry intersected, any permutation of S 6 other than ρ must intersect at most five rows just once. In that case, It would also intersect the remaining row just once and L would have a transversal. We conclude that no permutation can inersect more than four (= n − 2) rows exactly once.
11.4 The chromatic number of a latin square
In Bose(1963), that author introduced the concept of the latin square graph Γ(L) of a latin square L. (See page 312 of [DK1].) The vertices of this graph are the ordered triples (i, j, l ij ) which define L (see Section 1.4). Two vertices are adjacent if their triples have one component in common. Thus, an independent set of vertices represents a set of triples which differ in all three components and so define a partial transversal of L. The chromatic number χ(L) of L is defined to be the chromatic number of Γ(L) and so is the minimal number of partial transversals which cover the cells of L. 2
It follows immediately that, since each partial transversal of a latin square L of order n uses at most n cells, χ(L) ≥ n for every such latin square and, if L has an orthogonal mate, then χ(L) = n. It also follows that χ(L) is an invariant of the main class of L.
Suppose that χ(L) ≤ n + 1. Since n + 1 partial transversals each of length n − 1 cannot cover all the cells of L because (n + 1)(n − 1) < n 2, that would imply that L must have at least one partial transversal of length n. Thus, if we could show that χ(L) ≤ n + 1 for all latin squares of odd orders n, that would imply the truth of Ryser’s conjecture that every latin square of odd order has a transversal (see Section 1.5).
Suppose that χ(L) ≤ n + 2. Since n + 2 partial transversals each of length n − 2 cannot cover all the cells of L because (n + 2)(n − 2) < n 2, that would imply that L must have at least one partial transversal of length n − 1. So, if we could show that χ(L) ≤ n + 2 for all latin squares of order n, that would imply the truth of the Brualdi − Stein conjecture that every latin square has a partial transversal of length n − 1 (again see Section 1.5).
Further, it follows that, for a latin square (of order n) with no transversals (of which there are many of all even orders), χ(L) > n + 2 because n + 1 partial transversals each of length n − 1 or less cannot cover all the cells of L.
A bachelor latin square L b (that is, one without an orthogonal mate, see Section 9.1) has at most n − 1 full-length transversals but n − 1 full-length transversals and one partial transversal cannot cover all the cells of L b , so χ(L b ) ≥ (n − 1) + 2 = n + 1. Wanless and Webb(2006) have shown that such squares exist of all orders n ≥ 3.
Consequently, there exist latin squares of all even orders for which χ(L) ≥ n + 2 and latin squares of all orders n ≥ 3 for which χ(L) ≥ n + 1 so the conjectures of Brualdi-Stein and Ryser cannot be bettered.
Up to the present time, this alternative way of expressing these conjectures has not provided additional insight which might lead to their resolution.
For a latin square L of order n, the triple (R, C, S) is adjacent to n − 1 other triples (r, c, s) for which r = R (that is, triples in row R), adjacent to n − 1 others for which c = C (triples from column C) and adjacent to n − 1 for which s = S (triples representing cells containing symbol S), so Γ(L) is regular of valency (or degree) 3n − 3. It follows that χ(L) ≤ 3n − 2.
The above observations and upper bound for χ(L) are effctively given both in Cavenagh and Kuhl(2015) and in Besharati, Goddyn, Marmoodian and Mortezaeefar(2016). The first authors have also pointed out that, if we make use of Brook’s theorem 3 , we can improve the above bound to χ(L) ≤ 3n − 3.
If the latin square L (of order n) is row complete (see Section 2.6), the bounds χ(L) ≤ 3n − 2 or 3n − 3 can be reduced. Let h, k be an adjacent pair of entries in row r 1 of L so that (r 1, c 1 , h) and (r 1, c 1 + 1, k) are both triples of L. We give the vertex of Γ(L) which is labelled by (r 1, c 1 , h) colour k.
Now suppose that the vertices (r 1, c 1 ,h 1) and (r 2, c 2, h 2) are both given colour k so that (r 1, c 1 + 1, k) and (r 2, c 2 + 1, k) are both triples. Since symbol k cannot occur twice in any row or column, r 2 ≠ r 1 and c 2 ≠ c 1. Also, since the ordered pair of symbols h 1 , k can only occur once among the rows of L, h 2 ≠ h 1. Thus, the n − 1 vertices of Γ(L) which are coloured k by this prescription form a partial transversal of L. We require n further colours for the triples (vertices) which represent cells of the last column of L. So, for a row complete latin square of order n, χ(L) ≤ n + n = 2n.
The above argument was first given in Besharati et al (2016). The authors of that paper pointed out further that the upper bound χ(L) ≤ 3n − 2 could also be reduced if L has a partition into plexes. (See Section 3.5.)
A k-plex is a set of kn cells of L of which k are in each row, k are in each column and k contain each symbol. L is said to have a (k
1
, k
2
, . . ., k
h
)-partition if it is the union of a k
1-plex, a k
2-plex, . . . and a k
h
-plex. The subgraph of Γ(L) whose vertices are those of a k
i
-plex is a regular subgraph of valency 3k
i
− 3 (by the same argument as we used to show that Γ(L) itself is regular of valency at most 3n − 3) so we can colour the vertices of this subgraph with at most 3k
i
− 2 colours. (Note that Brook’s theorem is not applicable if any k
i
= 1 since then the corresponding subgraph consists of isolated vertices. Nor is it applicable if any k
i
= 2 and L has odd order.) Since, by hypothesis, the vertex set of Γ(L) is the union of the vertex sets of these subgraphs if L has a (k
1
, k
2
, . . ., k
h
)-partition, we get the upper bound
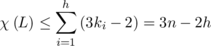 for such a latin square.
for such a latin square.
Th authors of both the papers previously mentioned went on to discuss upper bounds for the chromatic number χ(Z n ) of the Cayley table of a cyclic group Z n . Cavenagh and Kuhl used constructive arguments by which they actually showed how to cover the Cayley table with partial transversals. By this means, they proved that χ(Z 2m ) = 2m + 2 except when m is odd and divisible by 3. For the latter case, they were only able to establish the bound χ(Z 2m ) ≤ 2m + 3. [Since every group of odd order has an orthogonal mate, the result χ(Z 2m − 1) = 2m − 1 was already known.]
Besharati et al approached the problem in a different constructive way which they described graphically and which was not dependent on whether m is divisible by 2 and/or 3. They were able to improve the above result to show that χ(Z 2m ) = 2m + 2 in all cases.
The latter authors also calculated (with the aid of a computer) the values of χ(L) for all main classes of latin squares up to and including order 8. They found that χ(L) ≤ n + 2 for all latin squares of these orders and that χ(L) ≤ n + 1 for those of odd orders.
Finally, both sets of authors obtained an asymptotic bound for the chromatic number of any latin square L of order n to the effect that, when n → ∞, χ(L) ≤ n + o(n).
11.5 Practical applications of latin squares
(a) Latin squares and coding
Orthogonal latin squares have been used in coding theory for a number of different purposes: among others for designing error-detecting and correcting codes and in authentication. Early work on this topic, in particular that of Hamming(1950) and Golomb and Posner(1964), was described in [DK1]. Also Chapter 9 of [DK2] gave an account of developments in which latin squares play a role up to 1990. The many aspects of both coding theory and cryptography have now become the subject matter of several books so it seemed inappropriate to attempt a further update here. Instead, the reader is invited to look at Chapter 3 of Joyner and Kim(2011) for some unsolved problems.
(b) Latin squares as experimental designs
Since the 1930s, when the idea of doing so was pioneered by R.A. Fisher, latin squares and other related designs have been much used in the design of statistical experiments whose subsequent interpretation is to be effected with the aid of the procedure known as the “analysis of variance”. 4 We have already referred to such statistical applications in several earlier chapters of the present book: notably in Section 2.6, Section 5.6 and Section 6.4, where the uses of complete latin squares, of latin cubes and hypercubes, and of Room designs for this purpose were mentioned. By means of an example, we shall explain next the use of orthogonal latin squares for the same purpose.
Suppose that it is required to test the effect of five different treatments on yarn. Five looms are available for spinning the yarn and it is believed that both the loom used and the operator employed may affect the final texture of the spun yarn. If time were of no account, it would be desirable ideally to test the effect of every treatment with every operator and on every loom. However, by making use of the statistical technique of analysis of variance, a satisfactory test result can be obtained provided that each type of treated yarn is spun once on each loom and also once by each operator. If five operators are employed, the necessary set of twenty-five experiments can be specified by means of the 5 × 5 latin square illustrated in the left-hand diagram of Figure 11.5.1. Here, the columns 01, 02, 03, 04, 05 specify the operator and the rows L 1, L 2, L 3, L 4, L 5 specify which loom is to be used for the particular experiment. The entries Y 0, Y 1, Y 2, Y 3, Y 4 in the body of the square indicate which type of treated yarn is to be used. (Usually, one sample of yarn, called the control, is left untreated and the suffix 0 is used for this type of treatment.) Thus, in the first experiment, yarn Y 1 is to be spun by operator 01, on loom L 1. In another experiment, yarn Y 3 is to be spun by operator 02 on loom L 4. If it were also the case that the efficiency of the loom operators varied with the day of the week (five weekdays), this extra source of variation could be allowed for by using a 5 × 5 latin square which was orthogonal to the first to specify the day of the week on which each experiment was to be performed. Thus, in the right-hand square illustrated in Figure 11.5.1, the integers 0, 1, 2, 3, 4 are used to specify the five days of a week. Then each loom, each operator, and each type of treated yarn are associated with each day of the week just once.
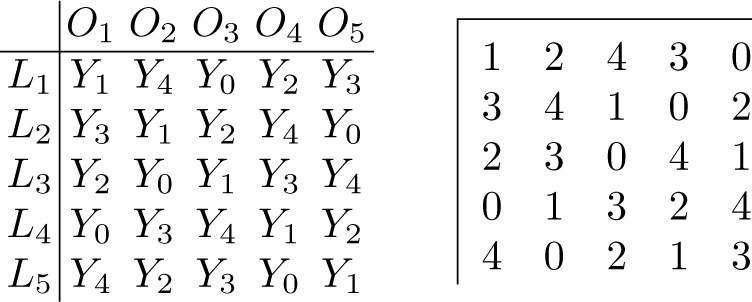
Fig. 11.5.1
The use of a latin square design for an experiment of the above kind is somewhat restrictive. It might happen, for example, that only four operators were available. This situation could be accommodated by using the same latin square with its last column deleted. It would still be the case that each type of yarn would be spun by each of the four remaining operators but now only four of the five different yarns would be spun on any one of the looms. A development of this observation gives rise to the concept of a balanced incomplete block design.
Balanced incomplete block designs were first introduced by F. Yates in Yates (1936). An example of such a design is given by the latin square used above when the last column is deleted. This has parameters b = 5, υ = 5, k = 4, r = 4, λ = 3.
A design for which property (iii) is satisfied is called pairwise balanced. More generally, if each set of t treatments occurs in exactly λt blocks, the design is called t-wise balanced or, more briefly, a t-design. A very well-known result is the following:
A BIBD for which b = υ and consequently r = k is said to be symmetric and such a design may also be referred to as a (υ, k, λ)-design.
Two obvious problems concerning BIBD’s are to provide methods of constructing them and to determine for what values of the parameters such designs exist. The second problem is not completely solved. As regards the first, many methods have been devised. Here, we mention that a symmetric BIBD is a finite projective plane or a complete set of MOLS. (See Section 5.2.) Also, a BIBD with k = 3 and λ = 1 is a Steiner triple system. (See Section 2.3.)
Chapter 10 of [DK2] is devoted to a quite detailed explanation of the appropriateness of the use of latin squares and other block designs in the design of experiments of various kinds and to an account of the analysis of the results, so we shall not repeat that account here.
An earlier account of the same topic is that of Hedayat and Shrikhande(1971).
(c) Designing games tounaments with the aid of latin squares
In Chapter 6, we discussed Room squares and their use for scheduling Bridge tournaments and we mentioned the related concept of a referee square first used for scheduling Rugby, which we shall now elaborate.
Such squares were first discussed by I. Anderson, Hamilton and Hilton in an unpublished manuscript.
Suppose that n = 2m + 1 ≥ 3 teams wish to compete in a league, each team playing every other team exactly once. The m(2m + 1) games required are to be scheduled for 2m + 1 days with m games on each day. Each team will have just one free day if it plays only once a day. It will be convenient if the schedule is such that the ith team has the ith day as its free day. Suppose further that each team selects/nominates a referee from among its own members or elsewhere.
If we number the days, the teams and the referees by 1, 2, …, 2m + 1 (so that referee i is the one selected by team i), is it possible to arrange the fixtures in such a way that (i) each referee referees each other team exactly once; (ii) no referee referees his own team; (iii) no referee has to referee two games on the same day; and (iv) the referee’s team plays on days when he is free to watch? Conditions (i) and (ii) imply that each referee referees m games.
In papers by Liaw(1998) and Dinitz and Ling(2001), it is proved that the answer is YES for all m > 0 except m = 2 and the solution given by these authors is such that referee i is always in action on his team’s rest day: that is, on day i. A solution of the latter kind gives rise to the concept of a referee square.
Such a square provides a solution to our scheduling problem when teams a and b play with referee i on day j if and only if {a, b} occurs in cell (i, j). An example for m = 3 taken from Liaw(1998) is given in Figure 11.5.2.
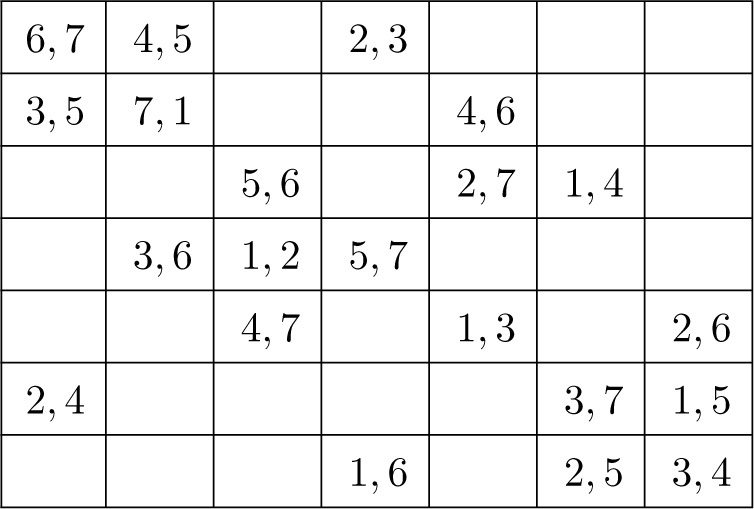
Fig. 11.5.2
Liaw’s main result is that such a square exists whenever 2m + 1 is composite. To obtain that result, he proved among other things that (i) if a Room square of side n exists, then referee squares of orders 3n and 5n exist; and (ii) if a Room square of side s, a referee square of side t and two MOLS of order t exist, then a referee square of side st can be constructed. Dinitz and Ling completed the proof of existence for all odd orders except five by using Liaw’s results and also several other combinatorial structures not discussed in the present book.
It is surprising how many games tournament requirments can be met with the aid of constructions using latin squares. In a survey paper of the present author, Keedwell(2000), solutions are provided for Round robin tournaments, Tennis on unequal courts, Home and away football, Balance in carry-over effects from one game in a tournament to the next, Mixed doubles tournaments, Spouse-avoiding mixed doubles, and Duplicate bridge and Whist. To save space, we shall not repeat the contents of that paper here but we shall draw attention to several papers not mentioned in it.
The first of these, Bedford, Ollis and Whittaker(2001), concerns balancing carry-over effects in a bipartite tournament between two teams of equal size where each player has to compete against each of the members of the opposing team and the solution makes use of a certain kind of directed terrace. (See Section 2.6 for the definition of the latter.)
The second, due to Preece and Phillips(2002), concerns the problem of scheduling bowls tournaments. A bowls team consists of 4n players, n ≥ 4, n playing lead position, n playing second position, n playing third position and n playing skip position. The problem is to assign the players to n rinks in n successive games in such a way that each rink contains one player for each position and no two players appear together more than once in any given rink. Solving this problem is equivalent to finding three mutually orthogonal Latin squares of order n. Adding the restriction that each player appears exactly once in each rink yields an enhanced problem that is equivalent to finding four mutually orthogonal Latin squares of order n.
The third paper, Berman and Smith(2012), discusses what the authors call a Mitchell tournament which is a variant of the famous type of tournament known as a spouse-avoiding mixed doubles round robin tennis tournament. The conditions for a Mitchell tournament differ from those for the type just mentioned only in the fact that a tournament of the latter type is not spouse-avoiding. For the construction, the authors use one square A which is column-latin and a second square B which is row-latin and such that A and B are orthogonal.
Finally, it is worth mentioning that scheduling a Round robin tournament for 2m teams or players is equivalent to finding a 1-factorization(see Section 8.3 for the definition) of the complete graph K2m as has been pointed out in Gelling and Odeh(1974). The teams are the vertices of K2m , the games are the edges, the rounds are the 1-factors.
The topic of devising games tournaments is still an active one so the above situations are not the only ones. In particular, I.Anderson(1997) has written a book on the subject and Berman has written several relevant papers on tournaments in addition to that mentioned above. [See, for example, Berman and Smith(2013) and D.R.Berman’s computer home page.]
11.6 Latin triangles
There have been several attempts to define a latin triangle. The most natural and appropriate of these in the opinion of the present author is that of Halberstam, Hoffman and Richter(1986) who gave a definition equivalent to the following:
A triangle of order n is an array in the shape of an equilateral triangle having n rows in each of the directions parallel to a side of the triangle with row i (1 ≤ i ≤ n) having n + 1 − i entries. The horizontal rows are called a-rows. The rows in the \-direction are called b-rows and the rows in the /-direction are called c-rows.
For the definition of a latin triangle of order n, or LT(n) for brevity, we need to distinguish between the cases n odd and n even. Let x ∈ {a, b, c}. For odd positive integers n, the line given by x = i for 2 ≤ i ≤ (n + 1)/2 is the union of the x-rows x = i and x = n + 2 − i. For even positive integers n, the line given by x = i for 1 ≤ i < n/2 is the union of the x-rows x = i and x = n + 1 − i.
A triangle is latin if and only if each of its a-lines, b-lines and c-lines contains each of a set S of distinct symbols exactly once. For an LT(2m) and for an LT(2m + 1), we need 2m + 1 symbols.
For instance, every LT(5) is equivalent to that shown in the left-hand array of Figure 11.6.1 and, in the right-hand array of Figure 11.6.1, we give an example of an LT(8).
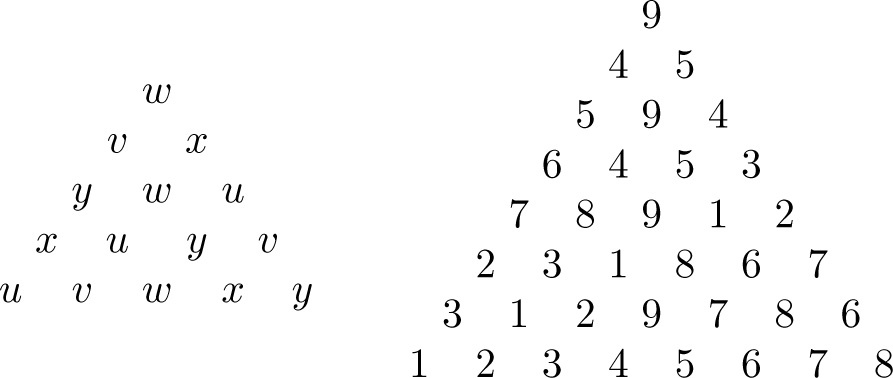
Fig. 11.6.1
Halberstam et al have constructed examples of latin triangles of all orders n ≤ 11 except n = 4, 6, 10 and have shown non-existence for the latter orders. They have also given a general construction valid for all orders n = 3 m and n = 3 m − 1.
In Halberstam and Richter(1989), examples of an LT(12), LT(13) and LT(15) have been obtained.
In a later paper by Alves, Gurganus, McLaurin and Smith(1991), these authors have obtained an LT(14) and have provided a construction of latin triangles of all odd orders n such that n + 2 is prime. They have thus obtained an LT(17) and an LT(21). They have also discussed how to define orthogonality of latin triangles. Halberstam et al had earlier proposed the definition that two latin triangles of the same odd order are orthogonal if, when they are superimposed, each unordered pair of symbols appears just once. (For even orders, their requirement is that each unordered pair of distinct symbols appears just once.) However, this property is not preserved if the symbols in one of the squares are permuted and it distinguishes between odd and even orders n, so Alves et al have proposed instead:
This definition includes the former one, does not distinguish beween odd and even orders and is unaffected by permutations of symbols. Alves et al have constructed a set of three latin triangles of order 7 which are mutually orthogonal with respect to the latter definition.
Many questions about this topic remain to be answered:
Do latin triangles exist of all odd orders and of all even orders except 4, 6 and 10? Alternatively, is there an integer n0 such that, for all n > n 0, an LT(n) exists?
For a given order n, how many different LT(n)’s exist? In this context, how should we define “different”?
What is the maximum number of mutually orthogonal LT(n)’s that can exist?
11.7 Latin squares and computers
When the first edition of this book was published, digital computers had been available for academic use to a limited extent for about 15 years and the idea of applying them in Algebra and Combinatorics was still quite novel. A first conference to discuss such applications had been held in Oxford in 1967 under the auspices of the Atlas Computing Laboratory, see Leech(1970). So the final chapter of [DK1] was devoted to describing the use of such computers as a new aid to the solution of latin square problems. In particular, techniques such as the back-track method for enumeration of latin squares and for the construction of sequencings of groups were described 5 . Also, the use of computers by Donald Knuth (later, the inventor of TEX) to enumerate all isomorphically distinct division rings of 32 elements and by one of the present authors to enumerate all D-neofields up to order 17, and a sample of order 18, was reported. To provide present-day readers with the flavour of that Chapter and because the problem raised remains unsolved, we reproduce the following short extract.
“Computers have been used as an aid in essentially two kinds of orthogonal latin square problems. In the first place, they have been used in searching for sets of mutually orthogonal latin squares of an assigned order n which shall contain as many squares as possible. In the second place, they have been used in attempts to construct new non-desargusian finite projective planes and hence complete sets of mutually orthogonal latin squares which would be non-equivalent to any previously known set.”
“The earliest search of the first kind known to the authors was that of Paige and Tomkins(1960). 6 These authors attempted to find a counter-example to the Euler conjecture by finding a pair of orthogonal latin squares of order 10, ten being the smallest integer greater than two and six which is an odd multiple of 2.”
“The first method they contemplated was to take a randomly generated 10 × 10 latin square and to use their SWAC computer to search directly for an orthogonal mate where, without loss of generality, the first rows of the two squares could be assumed to be the same. They estimated from trial runs that such a complete search would take of the order of 4.8 × 1011 machine hours for each initially selected square and they pointed out the difficulties of devising a method which would reject equivalent pairs of orthogonal squares and hence eliminate duplication of trials. They called two pairs equivalent if by rearranging rows, rearranging columns, or renaming the symbols of both squares of one pair simultaneously it would become either formally identical to the second pair or would differ from the second pair only in having its two squares oppositely ordered. (In the latter case, if L 1 and L 2 were the squares of one orthogonal pair, L 2 and L 1 would be those of the other.)”
“They then discussed a method by which only pairs of squares having a combinatorial pattern of such a kind that orthogonality would be possible would be constructed. This method involved identifying some of the symbols used in each latin square and is said to have been originally proposed by E. Seiden and W. Munro. Let us suppose that the symbols used in a given 10 × 10 latin square are the digits 0 to 9, and let each of the digits 0 to 4 be replaced by α and each of the digits 5 to 9 be replaced by β. In the resulting square, the symbols α and β each occur five times in each row and five times in each column. If there exists a second latin square orthogonal to the first which is similarly treated and if the two squares are then placed in juxtaposition, we shall get a 10 × 10 square matrix each element of which is one of the ordered pairs of symbols (or digraphs) αα, αβ, βα, or ββ, and with the following properties. Each of the four digraphs will occur all together 25 times in the matrix and in each row of the matrix there will be five digraphs whose first member is α and five whose first member is β, likewise five digraphs whose second member is α and five whose second member is β. The same statements will be true for the columns of the matrix. Such a square matrix was called admissible by Paige and Tomkins. They obtained further conditions which would have to be satisfied by a matrix constructed from two orthogonal latin squares in this way. The essentials of their computational procedure were first to compute an admissible 10 × 10 matrix and then to reverse the process just described by replacing the first member of each digraph by one of the digits 0 to 9 so as to get a latin square (α being replaced by one of the digits 0 to 4 and β by one of the digits 5 to 9) and subsequently to use the computer again to assign digits to all the cells of the partially specified orthogonal mate. That is, to enter one of the digits 0 to 4 in each α-cell and one of the digits 5 to 9 in each β-cell until one of the orthogonality conditions was violated. When a violation occurred, the programme backtracked in the usual manner to an earlier cell.”
“Unfortunately neither this nor the previous method was successful in producing an orthogonal pair of 10 × 10 latin squares despite the fact that more than 100 hours of computing time was used and, shortly afterwards, indeed even before the publication of Paige and Tomkins paper, the Euler conjecture was disproved by theoretical means. (See Chapter 11. 7 )”
“Almost immediately after the first counter-example to the Euler conjecture was obtained, E.T. Parker found a pair of orthogonal latin squares of order 10 by a construction which made use of statistical designs, and this sequence of events was regarded by many as a triumph for mathematical theory over computer search. However, not long afterwards, E.T. Parker himself initiated a new computer search for latin squares of order 10 which have orthogonal mates using a faster computer and a more sophisticated computer programme. The essential refinement was to generate and store all the transversals of a given 10 × 10 latin square and to search for disjoint sets of ten transversals (equivalent to finding an orthogonal mate) rather than to attempt to fill the cells of a partial orthogonal mate individually. E.T. Parker has given a full description of his method and results in Parker(1962a,1963). He discovered that 10 × 10 latin squares with orthogonal mates are not, in fact, particularly scarce and he also showed that there exist such squares with a large number of alternative orthogonal mates. His most striking result concerns the square displayed in Fig. 13.2.1 8 which has 5504 transversals and an estimated one million alternative orthogonal mates (that is, sets of 10 disjoint transversals). However, Parker was able to show by a partly theoretical argument that no two of these alternative orthogonal mates are themselves orthogonal and so, much to his own disappointment, he was not able to obtain a triad of mutually orthogonal 10 × 10 latin squares. The existence or non-existence of such triads remains an open question.”
It is remarkable that, 40 years later, this is still an open question though recent work, especially that in McKay, Meynert and Myrvold(2007), has made existence of such triads very unlikely.