This chapter deals with the second version of the memory allocation problem addressed in this book. This problem is related to the data binding problems introduced in section 1.3.3. Hence, the aim of this problem is to allocate the data structures from a given application to a given memory architecture. The main characteristic in the memory architecture is that the number of memory banks is fixed.
The memory allocation problem with constraint on the number of memory banks is equivalent to the k-weighted graph coloring problem [CAR 66]. To address this problem, we propose an ILP formulation and two metaheuristics based on both the tabu search method and an evolutionary algorithm that have originally been proposed for the vertex coloring problem. The proposed approaches are tested on a set of instances. The results produced by these metaheuristics are encouraging, and they suggest that the adaptation of methods from graph coloring is a promising way to address memory allocation problems in embedded systems.
In this chapter, we introduce the memory allocation problem with constraint on the number of memory banks. This problem is related to data binding problems presented in the optimization techniques for memory management and data assignment in section 1.3. Unlike the previous problem, which is focused on the design of memory architecture, in this problem the memory architecture is fixed. The purpose is to allocate data structures from a given application to memory banks of a given memory architecture.
In this version of the memory allocation problem, as in the memory partition problem for energy consumption (see section 1.3.3), the number of memory banks in the architecture is fixed. However, because of both different constraints considered and different objective functions to optimize, this version of the memory allocation problem is not equivalent to any problem related to the memory partition problem for energy consumption mentioned in section 1.3.3.
The number of available memory banks is limited because of cost and technological reasons. This is decided beforehand by the designer. Moreover, when the number of banks increases, both the communication resources required to transfer information and control logic increase at the same time. Hence, finding an optimal memory allocation for data structures with constraint on the maximum number of memory banks is extremely important [BEN 02c].
For this problem, we keep the assumptions on the target architecture from the previous chapter; that is the processor is able to simultaneously access all its memory banks, and the application to be implemented is provided as a C source code. Also, the data structures involved in the application have to be mapped into memory banks.
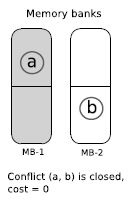
A conflict between two data structures is the same as it is defined in section 2.1. Moreover, we consider that each conflict has a cost, which is expressed in milliseconds (ms). This conflict cost is proportional to the number of times that the conflict appears in the application. Hence, the conflict’s statuses, open and closed, are defined as follows:
Figure 3.1. Closed conflict

In some cases, computing the conflict cost is not easy. Such a situation happens when the number of iterations of a loop cannot be forecasted (as in conditional instruction if or while loops). In this case, code profiling tools can be used for assessing conflict costs on a statistical basis [IVE 99, LEE 02].
Figure 3.2. Open conflict
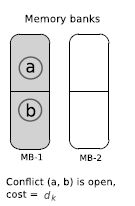
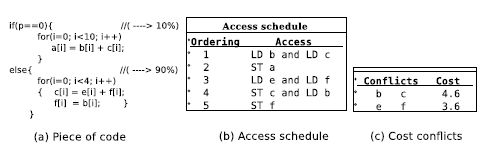
Figure 3.3 shows the access schedule and the cost conflicts for a piece of code. In this example, the probabilities of executing instructions if and else are 0.1 and 0.9, respectively. Data structures b and c are accessed in parallel two times in the schedule. Thus, the estimated conflict cost between data structures b and c is the number of iterations in the for loop multiplied by the probability of if instruction plus the product between the probability of else instruction and the number of iteration of its for loop, that is 10 × 0.1 + 4 × 0.9 ms. For the conflict between e and f, it is 4 × 0.9. Consequently, forecasting the cost conflicts depends on the occurrence probability of conditional instructions.
Figure 3.3. Cost conflict
This memory allocation problem, in addition to the fixed number of memory banks, takes into account the conflict costs. This problem, referred to as memory allocation with constraint on the number of memory banks, is stated as follows: for a given number of memory banks, we search for a memory allocation for data structures such that the total conflict cost generated by open conflicts is minimized. Section 3.3 presents an illustrative example that helps to understand this problem better.
The compiler often handles the allocation of data structures into memory banks; however, it does not produce optimal solutions. For this reason, section 3.2 presents an ILP formulation designed for this version of the memory allocation problem, and two metaheuristics are proposed in section 3.4, both are inspired by approaches designed to address the vertex graph coloring problem. The exact and heuristic approaches are compared in section 3.5.
The number of data structures is denoted by n, the number of conflicts is denoted by o, and a conflict k is modeled as the couple (k1, k2), where k1 and k2 are two data structures.
This problem considers a fixed number of memory banks denoted by m, and the conflict costs associated with the conflicts, which are denoted by dk for all k ∈ {1,…, o}.
The particular cases of auto-conflicts and isolated data structures (discussed in section 2.2) are taken into account in this ILP formulation and in the metaheuristic approaches.
There are two sets of decision variables: the first set is defined by equation [2.1]; it is the binary matrix X, where xi,j is set to 1 if data structure i is allocated to memory bank j, for all i in {1,…,n} and for all j in {1,…, m} (xi,j = 0, otherwise). The second set is a vector of real non-negative variables Y, which models the two conflict statuses, thus:
Thus, the integer linear program for this version of memory allocation problem is the following:
Equation [3.2] is the cost function of a memory allocation of the data structures to memory banks. It is equal to the total sum of open conflict costs.
The following constraints guarantee a feasible solution: equation [3.3] is equivalent to equation [2.4]; both ensure that each data structure is assigned to a single memory bank. Equation [3.4] sets variable yk to its appropriate value. Note that yk is equal to 1 if conflict k involves a data structure in conflict with itself (k1 = k2). Equation [3.5] enforces integrability constraint on xi,j. Finally, equation [3.6] sets yj as a non-negative variable for all j.
We suppose that the required information to formulate this problem is supplied by the embedded system designer, more precisely by the code profiling tools applied to the C source code of the application.
The number of memory banks describes the architecture of the chip, and the number of data structures describes the application, whereas the conflicts and their costs carry information on both the architecture and the application.
This problem, without the auto-conflicts and loops, is equivalent to the k-weighted graph coloring problem [CAR 66, VRE 03] (this problem is also referred to as the generalized graph coloring problem in [KOL 95]). It consists of coloring the vertices of an undirected weighted graph with at most k colors so as to minimize the sum of the weighted edges having both their endpoints colored with the same color. In this problem, the vertices represent data structures and each edge represents a conflict between a pair of data structures.
The ILP formulation for memory allocation problem with capacity constraints on memory banks can be addressed using a solver like GLPK [GNU 09] or Xpress-MP [FIC 09]. However, as shown by the computational tests in section 3.5, an optimal solution cannot be obtained in a reasonable amount of time for medium-size instances.
Moreover, as the k-weighted graph coloring problem is NP-hard [KAR 72, VRE 03], so is this version of memory allocation problem.
These are the reasons why we propose two metaheuristics to address this problem in section 3.4.
Vredeveld and Lenstra [VRE 03] tackle the k-weighted graph coloring problem using local search. In section 3.5, we compare the results reached by our metaheuristics, the ILP model and local search.
We take up again the example of Chapter 2, with the aim of illustrating the memory allocation problem with the constraint on the number of memory banks.
In this example, the purpose is to allocate the data structures of the LMS dual-channel filter algorithm [BES 04] to the available memory banks.
SoftExplorer [LAB 06] produces the information required from the source code C (see Figure 2.1). To display data, SoftExplorer changes the name of data structures by numbers. For this application, we have H11= 1, H12= 2, H21= 3, H22= 4, X1= 5, X2= 6, y1= 7 and y2= 8.
There are two memory banks, and Table 3.1 presents conflicts and their costs produced by SoftExplorer.
Table 3.1. Conflicts and costs of LMS dual-channel filter
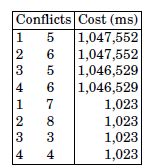
SoftExplorer computes the conflict cost using the access schedule. For example, conflict (1, 5) represents the conflict between data structures H11 and X1. These data structures are accessed in parallel twice (ordering 1 and 6 in the schedule of Figure 2.2). Also, the first time this conflict appears (line 17 of Figure 2.1), it is in a double loop for. Thus, the conflict cost is (L−1)2+(L−1), where L−1 = 1,023 (defined in line 4 of Figure 2.1) is the number of iterations in loops for.
A solution found by Xpress-MP is shown in Figure 3.4, where one can see the colored conflict graph and the allocation of data structures to two memory banks. The numbers on edges represent the conflict costs, and the loops are removed to state the k-weighted graph coloring problem.
Figure 3.4. Optimal solution for the example for the memory allocation with constraint on the number of memory banks
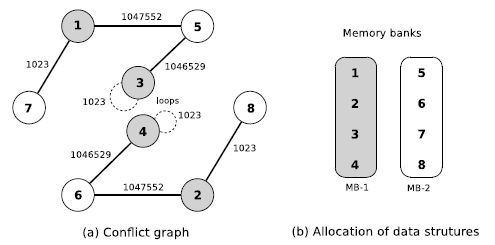
The chromatic number of this conflict graph is equal to the number of available memory banks thus all non-auto-conflicts are closed. The total cost of this memory allocation is the sum of the cost of the auto-conflicts; it is 2,046 ms.
As the memory allocation problem with constraint on the number of memory banks is equivalent to a graph coloring problem (k-weighted graph coloring problem), we propose two metaheuristics based on coloring approaches. The first metaheuristic is inspired from TabuCol, which is a tabu search for the vertex coloring problem presented by Hertz and Werra [HER 87]. The second metaheuristic is a hybrid evolutionary algorithm based on Evocol (Evolutionary Hybrid Algorithm for Graph Coloring), which is introduced by Porumbel et al. [POR 09b]. These proposed metaheuristics are described in more detail in the following sections.
The first metaheuristic implemented for this problem is called the Tabu-Allocation. It is based on the Tabucol algorithm, which is a tabu search for a vertex coloring problem.
The tabu search method [GLO 97] belongs to the local search methods. It relies on a simple procedure: it iteratively moves from the current solution to another solution in its neighborhood [SÖR 03]. The neighborhood of a solution depends on the characteristics of the addressed problem. The local search procedures stop when a local optimum is found. The tabu search escapes from the local optimum by prohibiting to move from the current solution to a solution presented in the tabu list, this is the origin of the method’s name. In general, the tabu list stores the last visited solution, and it is updated in the First In First Out (FIFO) principle.
Tabu-Allocation is a tabu search method developed here for the memory allocation problem with constraint on the number of memory banks. The considered neighborhood N(x) of a solution x is the set of solutions obtained from x by changing the allocation of a single data structure. For example, in a solution x, the data structure i is allocated to the memory bank j, so a possible neighbor solution x′ can be obtained by moving i to another memory bank and keeping the same allocation for the remaining data structures.
Thus, the tabu list contains the most recent moves of data structures. These moves are denoted by the pair (i, j), which means that data structure i cannot be mapped to memory bank j. We denote by NT the size of the tabu list, that is the maximum number of prohibited moves.
The main characteristic of Tabu-Allocation is that the size of the tabu list is not constant. Every N iterations, Tabu-Allocation randomly changes the size of the tabu list. It uses the function NT = a + N × t, where a is a fixed integer number and t is a random number between 0 and 2. This idea was inspired from Porumbel’s work about the vertex coloring problem [POR 09b]. This is, also somehow, related to a reactive tabu search [BAT 94].
Algorithm 3 describes the general structure of Tabu-Allocation.
The data required by the algorithm are the number of data structures, the number of memory banks, the conflicts between data structures and their respective costs and the two algorithm’s calibration parameters: the maximum number of iterations and the size of the tabu list. The algorithm returns the best memory allocation found for the data structures.
Tabu-Allocation starts with a random initial solution, that is data structures are randomly assigned to memory banks. Initial solutions generated in this way are feasible, because the capacity of memory banks is not taken into account in this version of memory allocation problem.
In the iterative phase, Algorithm 3 searches for the best solution in the neighborhood of the current solution during the maximum number of iterations, Niter. However, the research can stop before if a solution without open conflict is found because such a solution is optimal.
At each iteration, Tabu-Allocation seeks for the neighboring solution with minimum cost, no matter if it is worse than the current one.
Algorithm 3. Tabu-Allocation

To escape from local optima and to explore other regions of the search space, the method does not permit us to allocate a data structure i to its past memory bank j for NT iterations, that is: a new solution is accepted if the pair (i, j) is not in the tabu list.
The tabu list is updated on the FIFO principle whenever the current solution changes. The best solution Best is updated if the cost produced by the current solution is less than the cost of the best solution found so far.
The second metaheuristic implemented for this problem is called Evo-Allocation. It is inspired by an evolutionary hybrid algorithm for the vertex coloring problem.
Evo-Allocation keeps the following characteristics from Evocol [POR 09b]: a multiparent crossover, the general way of crossing parents and the variable size of tabu list. In fact, Evo-Allocation recourses to Tabu-Allocation for improving offspring.
The main difference between Evo-Allocation and Evocol is the way of updating population. Evo-Allocation considers the variance of the costs in the population to control diversity in the population.
Evo-Allocation is shown in Algorithm 4.
To execute the algorithm, the number of data structures, the number of memory banks and the two algorithms’ parameters, r, number of parents for the crossover and g, number of offsprings produced at each iteration, are required. The algorithm returns the best solution found.
The algorithm starts generating an initial population at random. The general principle of Evo-Allocation is to obtain g new offsprings (new solution) by crossing r different parents (i.e. r elements of the current population). The crossover selects, in each parent, the best assignments of data structures to form an offspring. Each offspring produced by this way is improved using Tabu-Allocation.
Algorithm 4. Evo-Allocation

Algorithm 5 describes the multiparent crossover. For each memory bank, the crossover chooses the allocations of data structures that minimizes the conflict rate. The conflict rate of a memory bank is the number of conflicts between its data structures, divided by the number of data structures mapped to this memory bank. The selected affectations are removed from each parent. Finally, to assign the remaining data structure, the algorithm chooses the memory bank that produces the minimum number of open conflicts.
Evo-Allocation produces an offspring if the distance to its parents is greater than a fixed threshold. The distance between two solutions sa and sb is defined as the minimum number of data structures that need to be moved from the first solution to become equal to the second solution. This definition is frequently used in graph coloring [GAL 99].
Algorithm 5. Crossover-Evo-Allocation
At each iteration, Evo-Allocation improves the quality of the population by replacing the g parents that have the highest cost with g offspring.
With the aim of ensuring diversity, Evo-Allocation considers the statistic variance of solution costs. If this variance is less than the fixed threshold, then a new population is randomly generated.
Thus, the population is updated with the offspring and with the variance criterion. This way of updating the population is a trade-off between diversity and quality.
This section presents the instances used for the computational test, and the relevant aspects about the implementation of the proposed metaheuristics. Moreover, we present the results produced by our algorithms, and we compare these results with results of the ILP model and the local search method.
We have used 17 instances to test our approaches. The instance mpeg2enc is a real electronic problem provided by the Lab-STICC laboratory. No more real-life instances are available for this problem, so we have tested our algorithms using a set of instances that originates from DIMACS [POR 09a], a well-known collection of graph coloring instances. These instances have been enriched by generating edge costs at random so as to create conflict costs. For this, we have used the uniform law in the interval [1; 100].
Our metaheuristics have been implemented in C++ and compiled with gcc 4.11. The PC used is a 3 GHz Intel® Pentium IV with and 1 GB of RAM.
To execute Tabu-Allocation, we set the number of iterations Niter equal to 10,000, and the integer numbers a and N used in function to calculate the size of the tabu list (NT = a + N × t) are set to 50 and 10, respectively. We set these values based on our computational tests.
The calibration parameters of Evo-Allocation have the same value as in Evocol [POR 09b]: a population constituted of d = 15 elements, a crossover with three parents (r = 3) and the generation of three offspring (g = 3). The Tabu-Allocation embedded in Evo-Allocation is run with Niter equal to 1,000.
The acceptance threshold for the distance between two elements of the population is R = 0, 1 × n. We have fixed a threshold of 0.3 for the variance of the population, and 100 iterations as the stopping criterion.
To our best knowledge, there are no alternative approaches for this problem in the literature. The k-weighted graph coloring problem can be addressed by Local Search [VRE 03], so we have tested the local search on instances of this memory allocation problem. To this end, we have used LocalSolver 1.0 [INN 10], which is a solver for combinatorial optimization entirely based on local search. This solver addresses a combinatorial optimization problem by performing autonomous moves, which can be viewed as a structured ejection chains applied to the hypergraph induced by boolean variables and constraints [REG 04]. Results of that method are also reported.
Table 3.2 provides the best cost reached by the metaheuristics, the local search solved with LocalSolver and also by the ILP formulation solved by GLPK [GNU 09]. The CPU time, in seconds, is provided for each method. The first two columns are the main features of the instances: name, number of data structures, number of conflicts and number of memory banks. The instances are sorted in a non-decreasing order of the number of conflicts. The last column shows each instance, if the solution found by GLPK is optimal or not, as we have set a time limit of 1 h for each instance.
The last lines of Table 3.2 give a summary for each approach used in this experiment; it is the number of optimal solutions, the number of best solutions and the average CPU time.
Table 3.2. Results
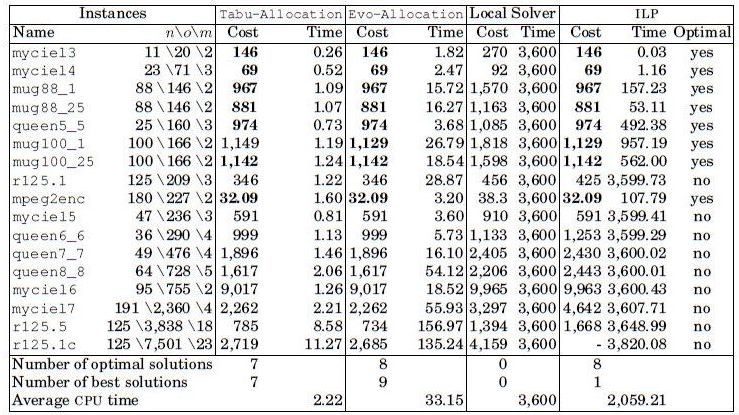
The computational results show that Evo-Allocation reaches the optimal solution when it is known, that is when the ILP can be solved to optimality within one hour. Obviously, Tabu-Allocation is faster than Evo-Allocation because Tabu-Allocation is a subprogram of Evo-Allocation. The local search has not reached the optimal solution for any instance after one hour of computation.
When the optimal solution is not found after one hour of computation for the ILP, the solution returned is worse than the solutions generated by the metaheuristics. Also, note that GLPK has not found any integer solution for the instance r125.1c after one hour of computation.
In addition to the ILP formulation, this chapter has introduced two metaheuristics: Evo-Allocation based on an hybrid evolutionary algorithm and Tabu-Allocation based on the tabu search method. These metaheuristics are inspired by the algorithms for the vertex coloring problem because this version of memory allocation problem can be seen as the k-weighted graph coloring problem.
The best results are returned by Evo-Allocation, which has a rigorous control of population diversity and a multiparent crossover. The main difference between Tabu-Allocation and a classical tabu search is the variable size of the tabu list.
Table 3.2 compares the results between metaheuristics and exact formulation solved with Xpress-MP. The experimental results are encouraging and suggest that the solutions found are of very good quality, even for larger instances for which the optimal solution is unknown.
Finally, the results suggest that the methods from graph coloring can be successfully extended to more complex memory allocation problems in embedded systems, which is done in the rest of this book.
The work presented in this chapter has been published in the proceedings of ROADEF (Congrès de la société Française de Recherche Opérationnelle et d’Aide à la Décision) [SOT 10].