10

Simplifying Polynomial Expressions

In this chapter, you apply your skills in multiplying polynomials to the process of simplifying polynomial expressions.

Identifying Polynomial Expressions

A polynomial expression is composed of poly­nomials only and can contain grouping symbols, multiplication, addition, subtraction, and raising to nonzero powers only.

No division by polynomials or raising polynomials to negative powers is allowed in a polynomial expression.

Problem   Specify whether the expression is a polynomial expression.

a. 5 + 2(a − 5)

b.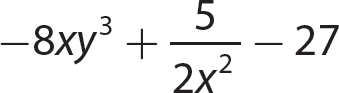

c. (2x − 1)(3x − 4) + (x − 1)²

d. 4(x ⁻³ − y²) + 5(x + y ⁻¹)

e.

f. 2x² − x − 4[3x + 5(x − 4)]

Solution

a. 5 + 2(a − 5)

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

5 + 2(a − 5) is composed of polynomials and contains permissible components, so it is a polynomial expression.

b.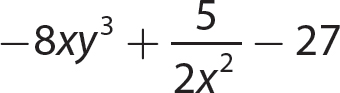

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

is not a polynomial expression because it contains division by x².

c. (2x − 1)(3x − 4) + (x − 1)²

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

(2x − 1)(3x − 4) + (x − 1)² is composed of polynomials and contains permissible components, so it is a polynomial expression.

d. 4(x⁻³ − y²) + 5(x + y⁻¹)

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

4(x ⁻³ − y²) + 5(x + y ⁻¹) is not a polynomial expression because it is not composed of polynomials due to negative exponents.

e.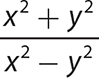

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

is not a polynomial expression because it contains division by a non-constant polynomial.

f. 2x² − x − 4[3x + 5(x − 4)]

Step 1.   Check whether the expression meets the criteria for a polynomial expression.

2x² − x − 4[3x + 5(x − 4)] is composed of polynomials and contains permissible components, so it is a polynomial expression.

Simplifying Polynomial Expressions

When you simplify polynomial expressions, you proceed in an orderly fashion so that you do not violate the order of operations for real numbers. After all, the variables in polynomials are simply stand-ins for real numbers, so it is important that what you do is consistent with the rules for working with real numbers.

Simplifying Polynomial Expressions

To simplify a polynomial expression:

  1. Simplify within grouping symbols, if any. Start with the innermost grouping symbol and work outward.

  2. Do powers, if indicated.

  3. Do multiplication, if indicated.

  4. Simplify the result.

Problem   Simplify.

a. 5 + 2(a − 5)

b. − 3(y + 4) + 8y

c. 9xy − x(3y − 5x) − 2x²

d. (2x − 1)(3x − 4) + (x − 1)²

e. 2x² − x − 4[3x + 5(x − 4)]

f. 2(x + 1)²

Solution

a. 5 + 2(a − 5)

Step 1.   Do multiplication: 2(a − 5).

5 + 2(a − 5)

= 5 + 2a − 10

Step 2.   Simplify the result.

= 2a − 5

Step 3.   Review the main steps.

5 + 2(a − 5) = 5 + 2a − 10 = 2a − 5

5 + 2(a − 5) ≠ 7(a − 5). Do multiplication before addition, if no parentheses indicate otherwise.

b. − 3(y + 4) + 8y

Step 1.   Do multiplication: − 3(y + 4).

− 3(y + 4) + 8y

= − 3y − 12 + 8y

Step 2.   Simplify the result.

= 5y − 12

Step 3.   Review the main steps.

− 3(y + 4) + 8y = − 3y − 12 + 8y = 5y − 12

c. 9xy − x(3y − 5x) − 2x²

Step 1.   Do multiplication: − x(3y − 5x).

9xy − x(3y − 5x) − 2x²

= 9xy − 3xy + 5x² − 2x²

Step 2.   Simplify the result.

= 3x² + 6xy Write answer in descending powers of x.

Step 3.   Review the main steps.

9xy − x(3y − 5x) − 2x² = 9xy − 3xy + 5x² − 2x² = 3x² + 6xy

d. (2x − 1)(3x − 4) + (x − 1)²

Step 1.   Do the power: (x − 1)².

(2x − 1)(3x − 4) + (x − 1)²

(2x − 1)(3x − 4) + x² − 2x + 1

Step 2.   Do multiplication: (2x − 1)(3x − 4).

= 6x² − 11x + 4 + x² − 2x + 1

Step 3.   Simplify the results.

= 7x² − 13x + 5

Step 4.   Review the main steps.

(2x − 1)(3x − 4) + (x − 1)² = 6x² − 11x + 4 + x² − 2x + 1 = 7x² − 13x + 5

e. 2x² − x − 4[3x + 5(x − 4)]

Step 1.   Simplify within the brackets. First, do multiplication: 5(x − 4).

2x² − x − 4[3x + 5(x − 4)]

2x² − x − 4[3x + 5x − 20]

Step 2.   Simplify 3x + 5x − 20 within the brackets.

= 2x² − x − 4[8x − 20]

Step 3.   Do multiplication: − 4[8x − 20].

= 2x² − x − 32x + 80

Step 4.   Simplify the result.

= 2x² − 33x + 80

Step 5.   Review the main steps.

2x² − x − 4[3x + 5(x − 4)] = 2x² − x − 4[3x + 5x − 20]

2x² − x − 4[8x − 20]

2x² − x − 32x + 80 = 2x² − 33x + 80

f. 2(x + 1)²

Step 1.   Do the power: (x + 1)².

= 2(x² + 2x + 1)

2(x + 1)² ≠ (2x + 2)². The exponent applies only to (x + 1).

Step 2.   Do multiplication: 2(x² + 2x + 1).

= 2x² + 4x + 2

Step 3.   Review the main steps.

2(x + 1)² = 2(x² + 2x + 1) = 2x² + 4x + 2

Exercise 10

Simplify.

1. 8 +2(x − 5)

2. −7(y − 4)+ 9y

3. 10xy − x(5y − 3x) − 4x²

4. (3x − 1)(2x − 5)+(x +1)²

5. 3x² − 4x − 5[x − 2(x − 8)]

6. − x(x + 4)+5(x − 2)

7. (a − 5)(a +2) − (a − 6)(a − 4)

8. 5x² − (− 3xy − 2y²)

9. x² − [2x − x(3x − 1)]+ 6x

10. (4x²y⁵)(− 2xy³)(− 3xy) − 15x² y³(2x² y⁶ + 2)