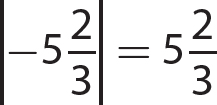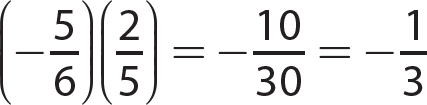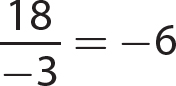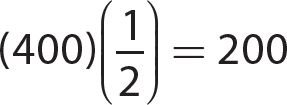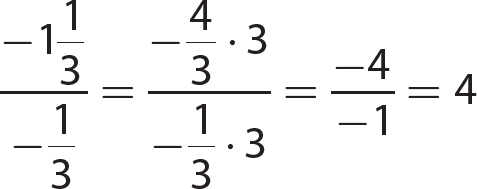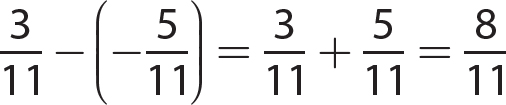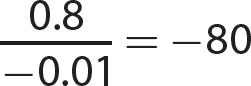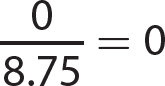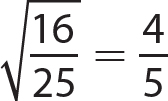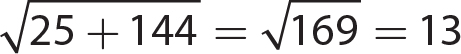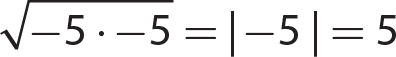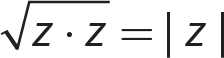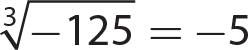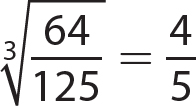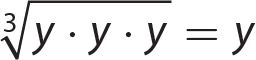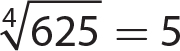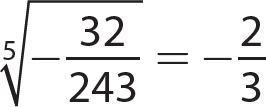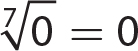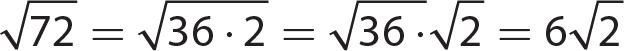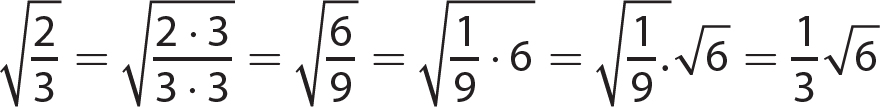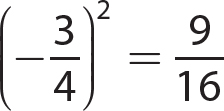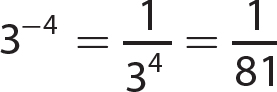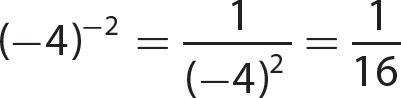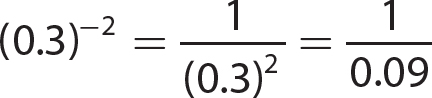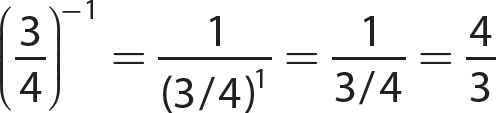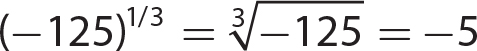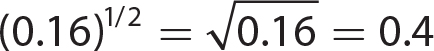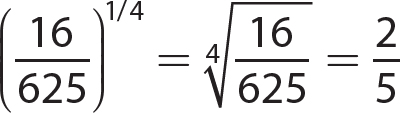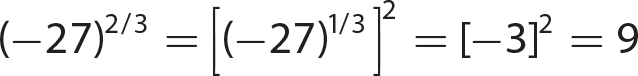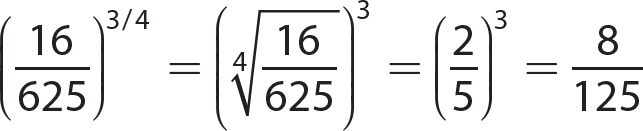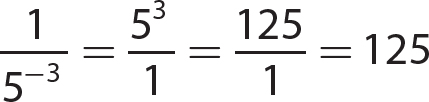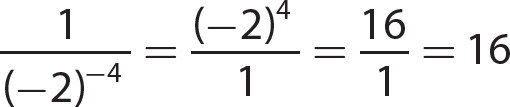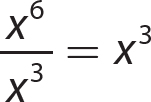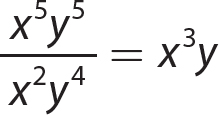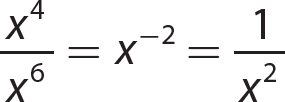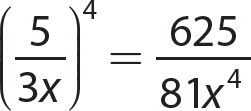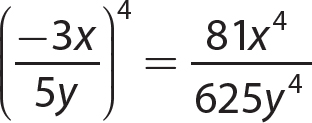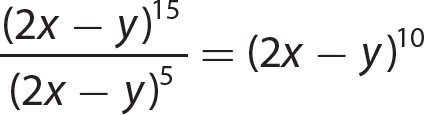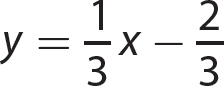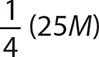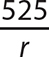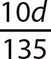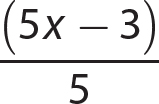Chapter 1 Numbers of Algebra
Exercise 1
1. 10 is a natural number, a whole number, an integer, a rational number, and a real number.
2. 
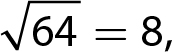which is a natural number, a whole number, an integer, a rational number, and a real number.
3. 
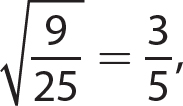which is a rational number and a real number.
4. −π is an irrational number and a real number.
5. −1,000 is an integer, a rational number, and a real number.
6. 
is an irrational number and a real number.
7. 
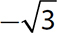is an irrational number and a real number.
8. 
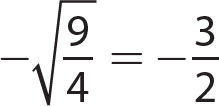is a rational number and a real number.
9. 1 is a natural number, a whole number, an integer, a rational number, and a real number.
10. 
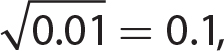which is a rational number and a real number.
11. Closure property of multiplication
12. Commutative property of addition
13. Multiplicative inverse property
14. Closure property of addition
15. Associative property of addition
16. Distributive property
17. Additive inverse property
18. Zero factor property
19. Associative property of multiplication
20. Multiplicative identity property
Chapter 2 Computation with Real Numbers
Exercise 2
1. |−45| = 45
2. |5.8| = 5.8
4. “Negative nine plus the opposite of negative four equals negative nine plus four”
5. “Negative nine minus negative four equals negative nine plus four”
6. −80 + −40 = −120
7. 0.7 + −1.4 = −0.7
10. (−100)(−8) = 800
13. −450.95 − (−65.83) = −450.95 + 65.83 = −385.12
16. −458 + 0 = −458
20. (−3)(1)(−1)(−5)(−2)(2)(−10) = −600
Chapter 3 Roots and Radicals
Exercise 3
1. 12 and −12
3. 0.8 and −0.8
4. 20 and −20
6. 
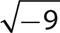not a real number
17. 
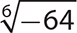not a real number
Chapter 4 Exponentiation
Exercise 4
1. −4 · −4 · −4 · −4 · −4 = (−4)5
2. 8 · 8 · 8 · 8 · 8 · 8 · 8 = 87
3. (−2)7 = −128
4. (0.3)4 = 0.0081
6. −24 = −16
7. (1 + 1)5 = 25 = 32
8. (−2)0 = 1
15. 
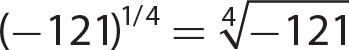not a real number
Chapter 5 Order of Operations
Exercise 5
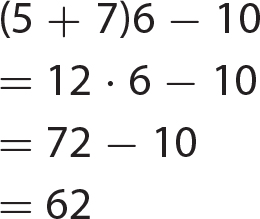
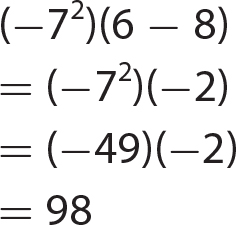
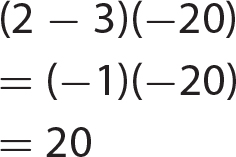
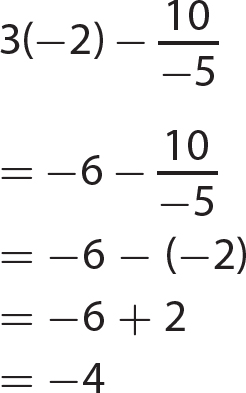
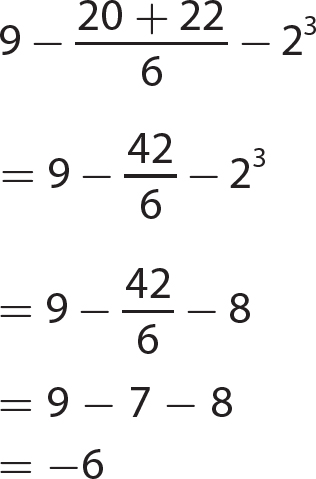
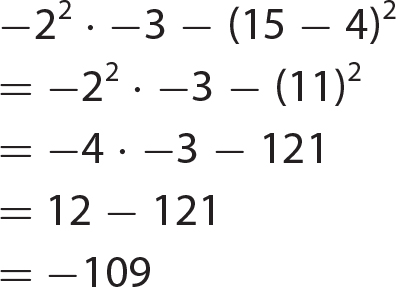
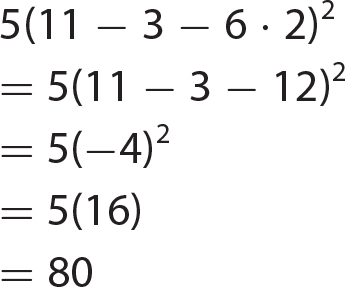
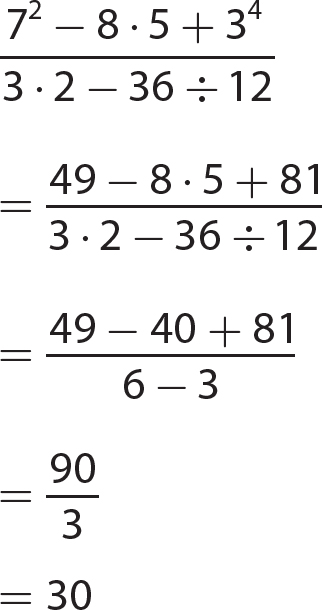
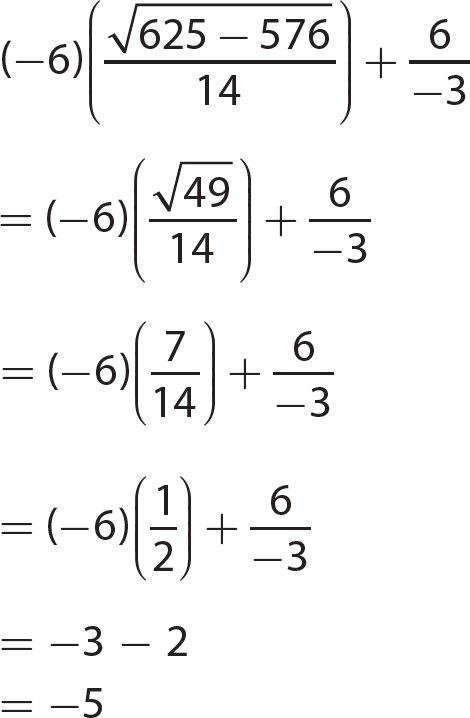
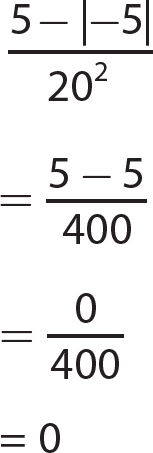
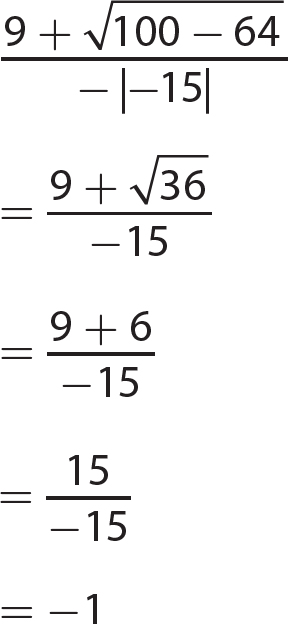
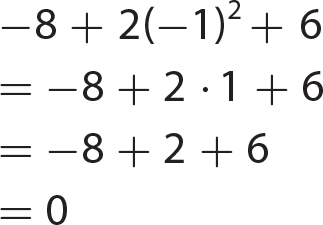
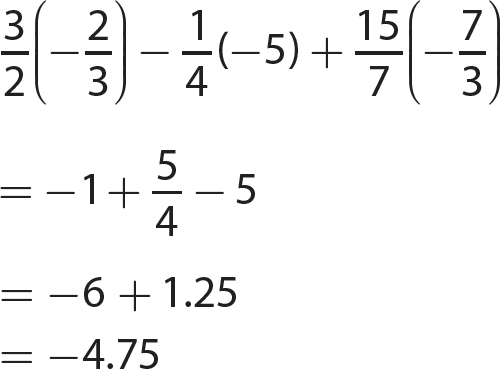
Chapter 6 Algebraic Expressions
Exercise 6
1. The letter r stands for the measure of the radius of a circle and can be any real nonzero number, so r is a variable. The numbers 2 and π have fixed, definite values, so they are constants.
2. −12 is the numerical coefficient
3. 1 is the numerical coefficient
4. 
is the numerical coefficient
5. −5x = −5 · 9 = −45
6. 2xyz = 2(9)(−2)(−3) = 108
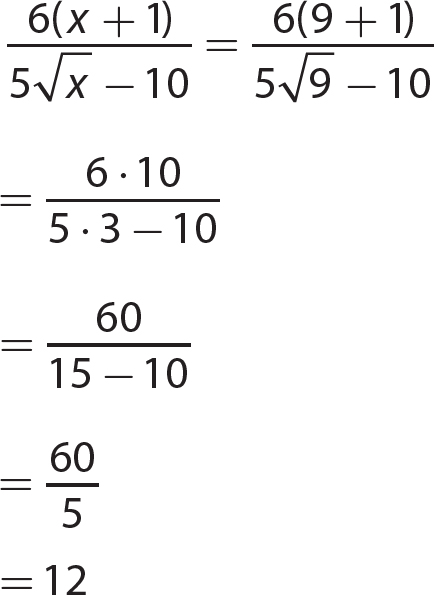
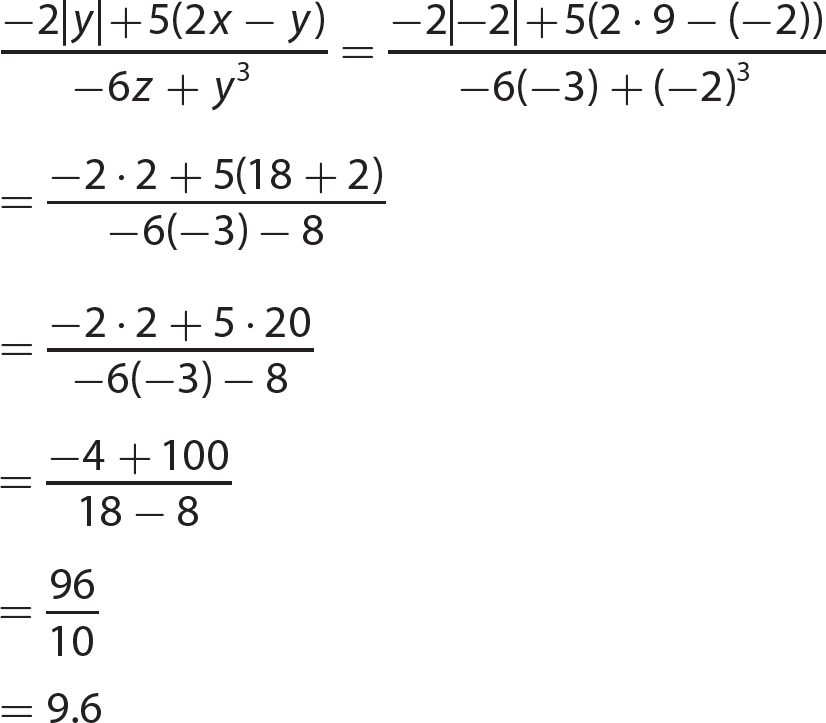
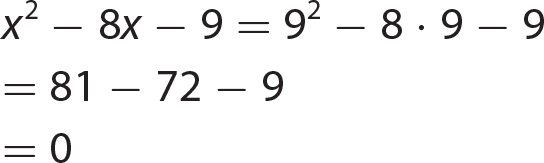
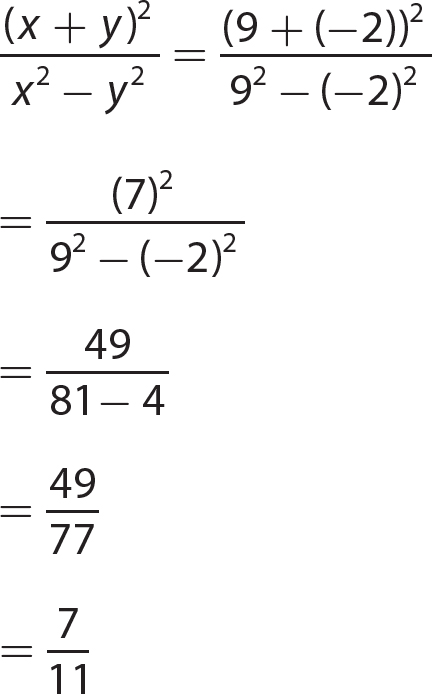
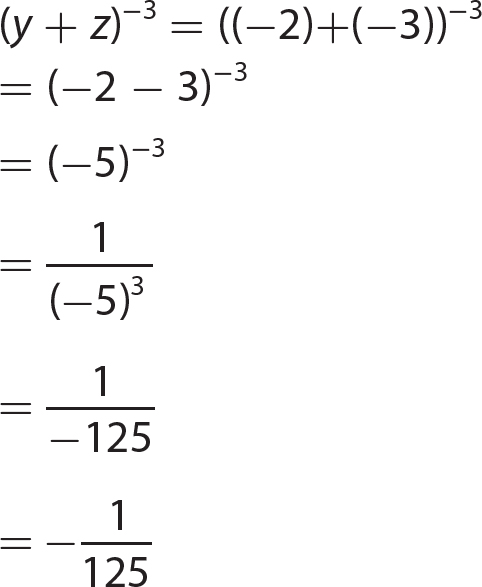
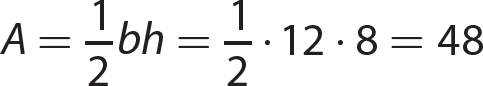
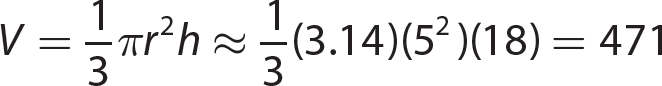
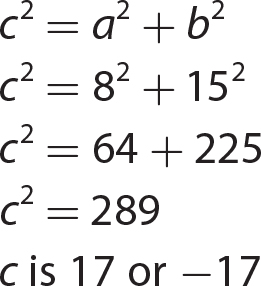
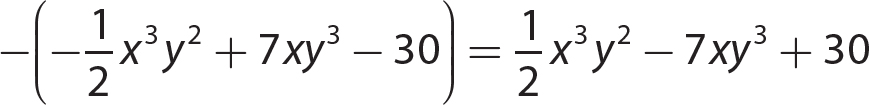
17. (8a3 + 64b3) = 8a3 + 64b3
18. −4 − (−2y3) = −4 + 2y3
19. −3(x + 4) = −3x − 12
20. 12 + (x2 + y) = 12 + x2 + y
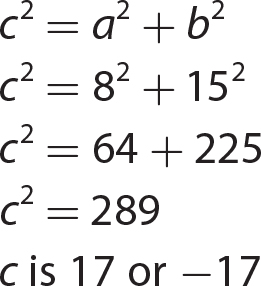
Chapter 7 Rules for Exponents
Exercise 7
1. x4x9 = x13
2. x3x4y6y5 = x7y11
6. (x2)5 = x10
7. (xy)5 = x5y5
8. (−5x)3 = −125x3
9. (−2x5yz3)4 = 16x20y4z12
12. (2x + 1)2 is a power of a sum. It cannot be simplified using only rules for exponents.
13. (3x − 5)3 is a power of a difference. It cannot be simplified using only rules for exponents.
14. (x + 3)(x + 3)2 = (x + 3)3
Chapter 8 Adding and Subtracting Polynomials
Exercise 8
1. x2 − x + 1 is a trinomial.
2. 125x3 − 64y3 is a binomial.
3. 2x2 + 7x − 4 is a trinomial.
4. 
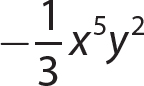is a monomial.
5. 2x4 + 3x3 − 7x2 − x + 8 is a polynomial.
6. −15x + 17x = 2x
7. 14xy3 − 7x3y2 issimplified.
8. 10x2 − 2x2 − 20x2 = −12x2
9. 10 + 10x is simplified.
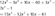
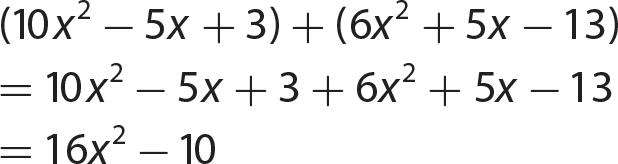
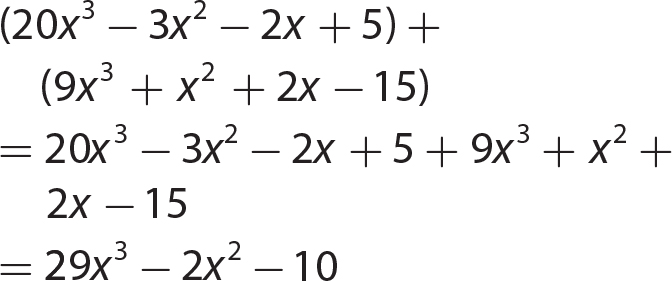
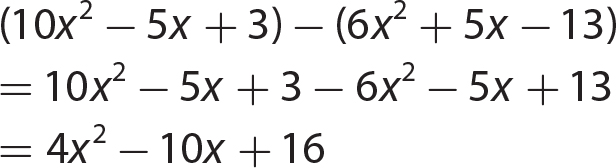
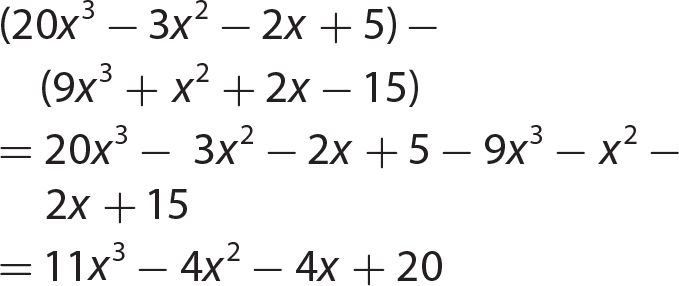
Chapter 9 Multiplying Polynomials
Exercise 9
1. (4x5y3)(−3x2y3) = −12x7y6
2. (−8a4b3)(5ab2) = −40a5b5
3. (−10x3)(−2x2) = 20x5
4. (−3x2y5)(6xy4)(−2xy) = 36xy10
5. 3(x − 5) = 3x − 15
6. x(3x2 − 4) = 3x3 − 4x
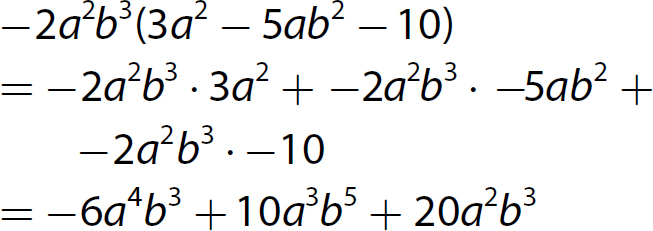
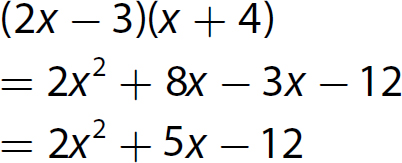
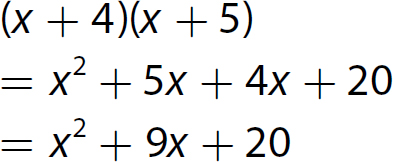
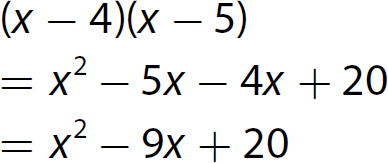
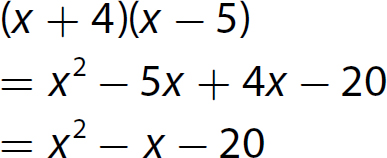
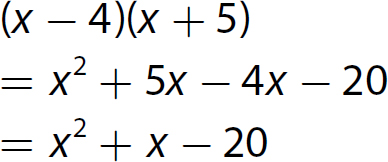
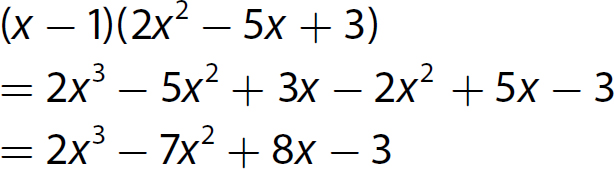
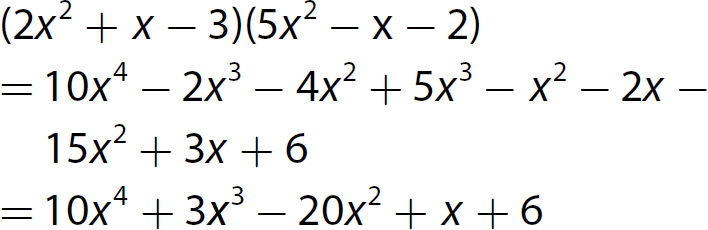
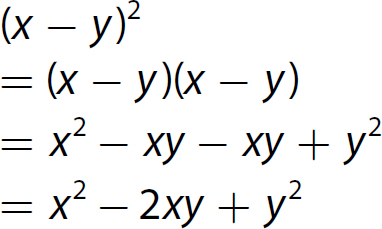
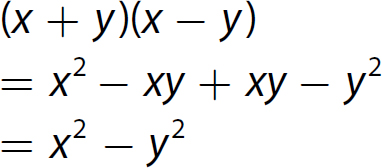
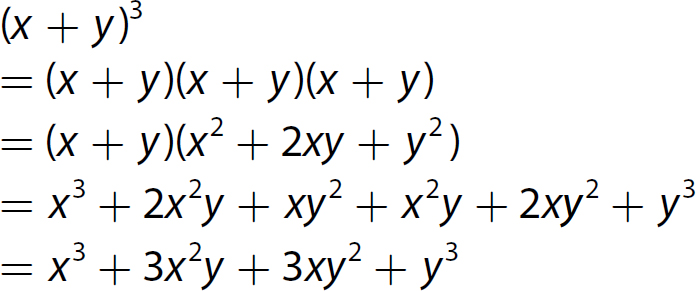
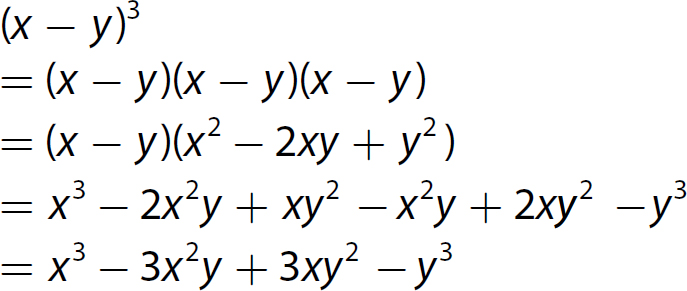
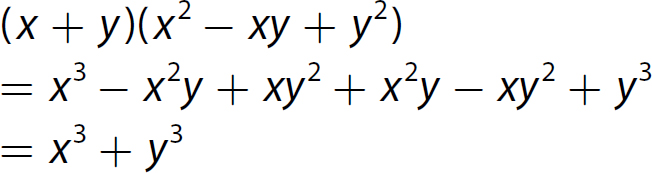
Chapter 10 Simplifying Polynomial Expressions
Exercise 10
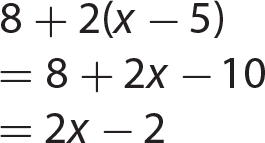
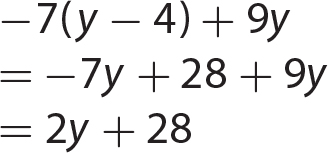
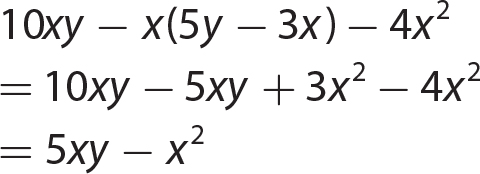
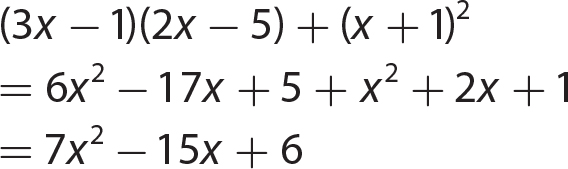
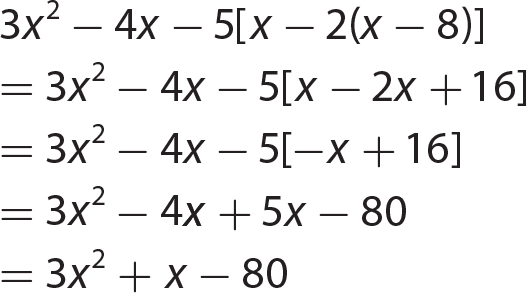
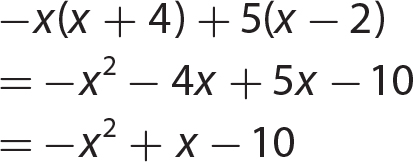
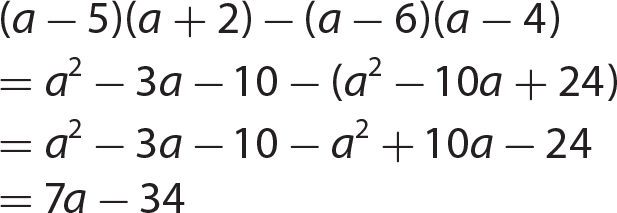
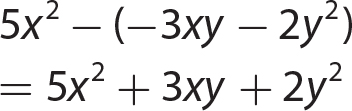
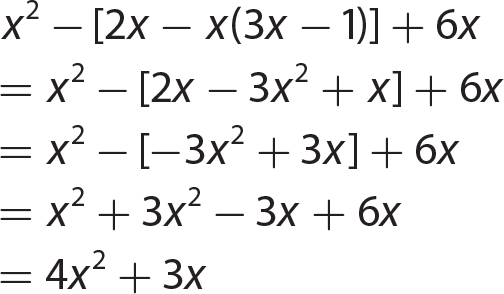
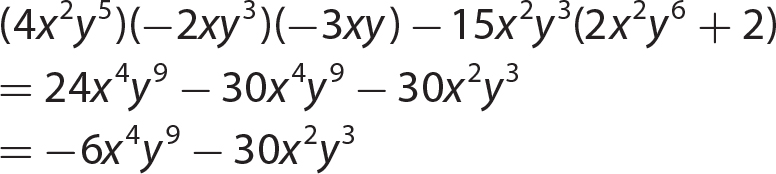
Chapter 11 Dividing Polynomials
Exercise 11
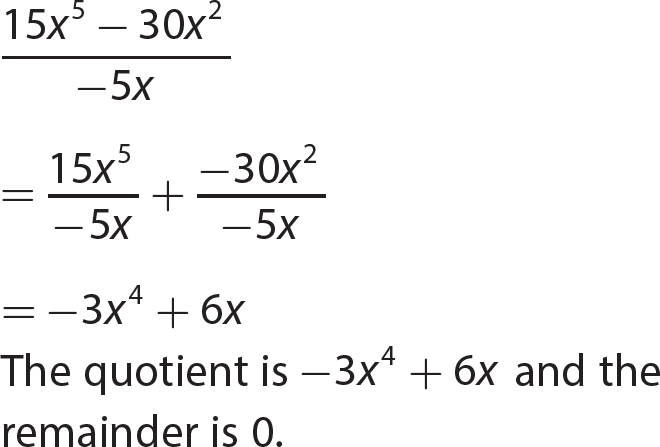
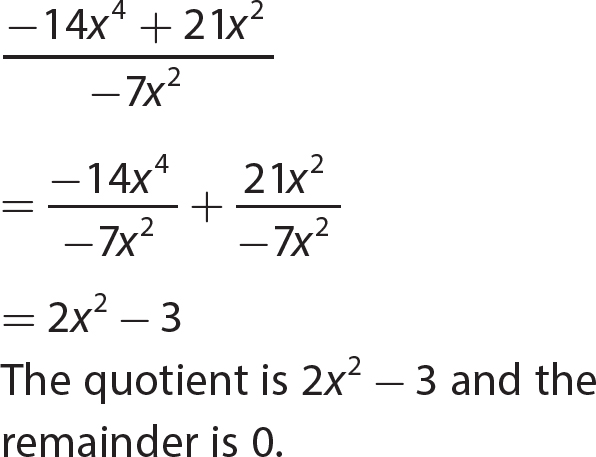
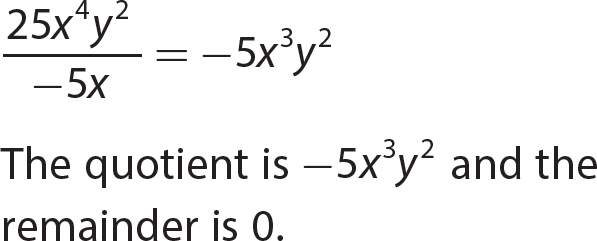
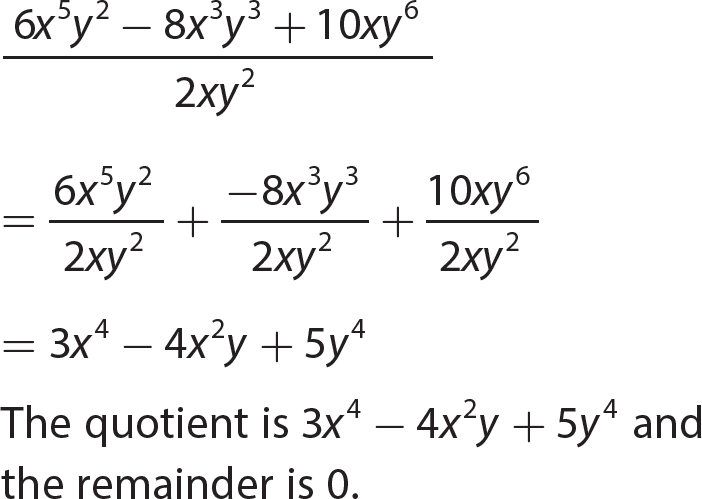
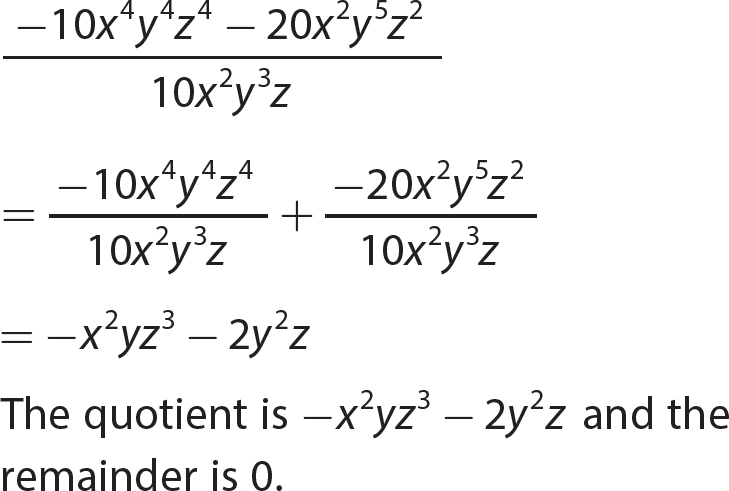
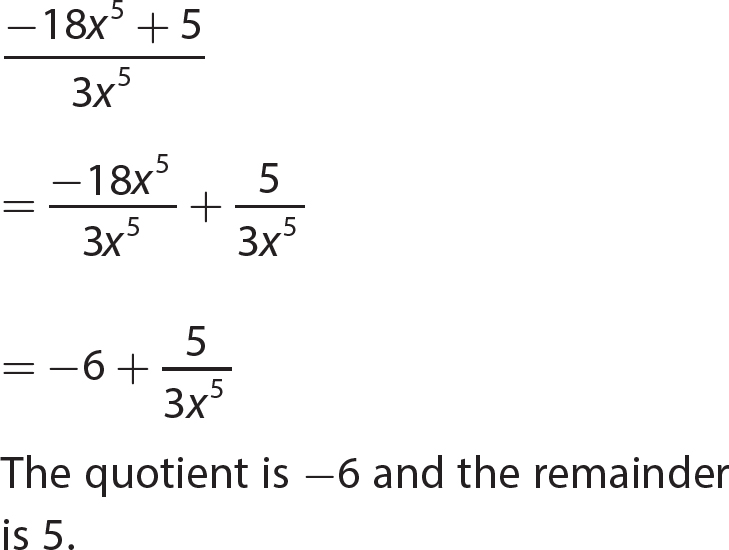
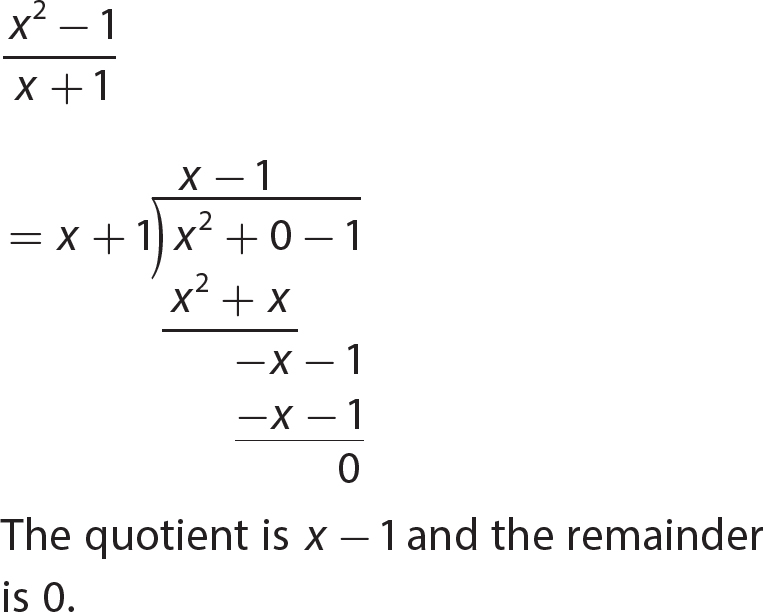
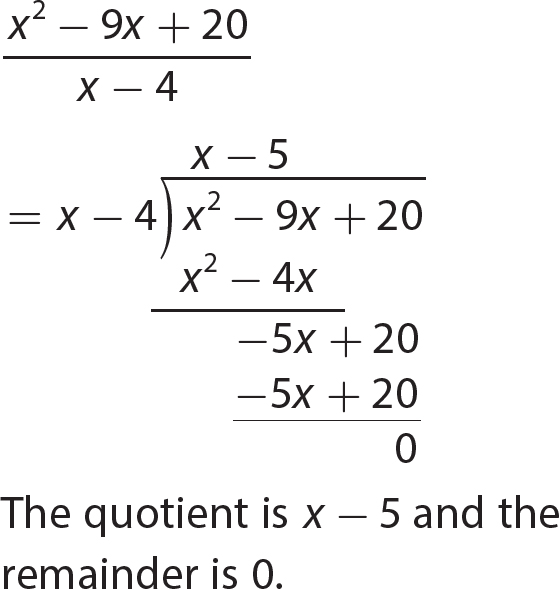
Chapter 12 Factoring Polynomials
Exercise 12
1. False
2. False
3. False
4. False
5. False
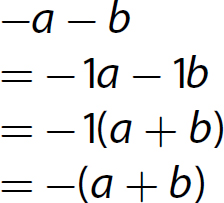
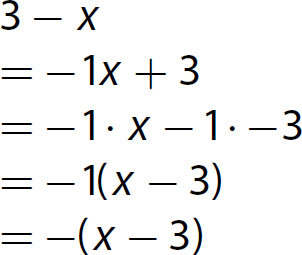
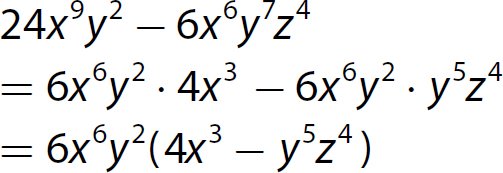
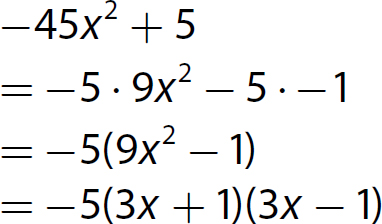
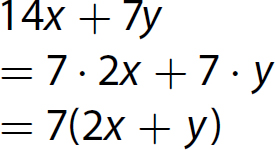
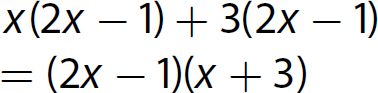
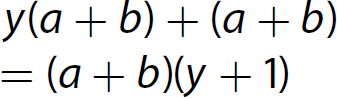
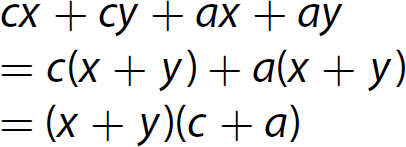
17. x2 − 3x −4 = (x − 4)(x + 1)
18. x2 − 49 = (x + 7)(x − 7)
19. 6x2 + x − 15 = (3x + 5)(2x − 3)
20. 16x2 − 25y2 = (4x + 5y)(4x − 5y)
21. 27x3 − 64 = (3x − 4)(9x2 + 12x + 16)
22. 8a3 + 125b3 = (2a + 5b)(4a2 − 10ab + 25b2)
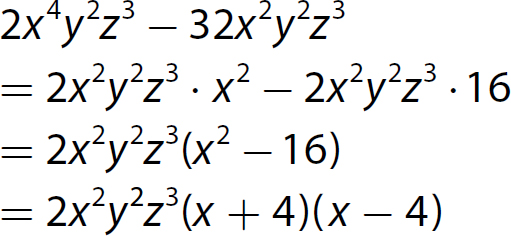
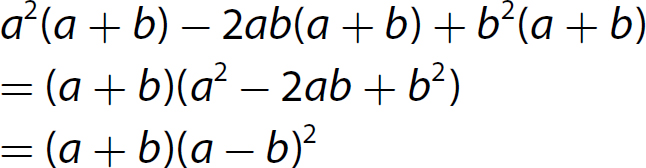
Chapter 13 Rational Expressions
Exercise 13
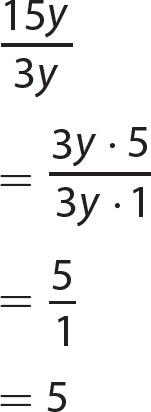
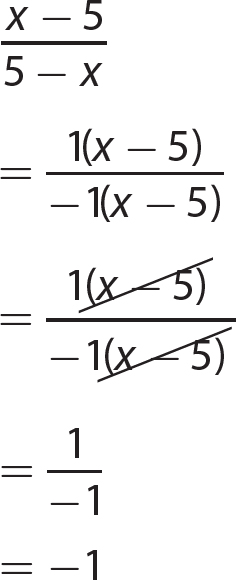
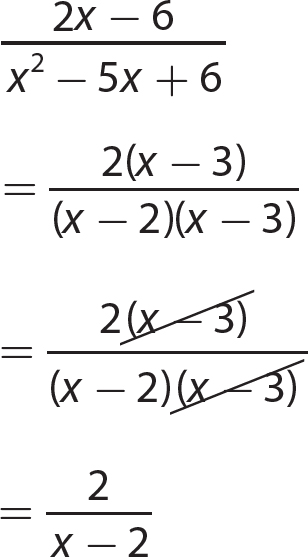
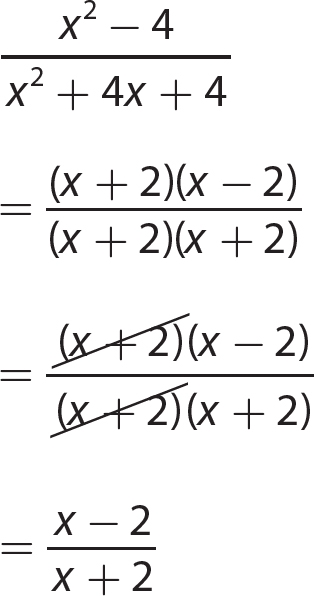
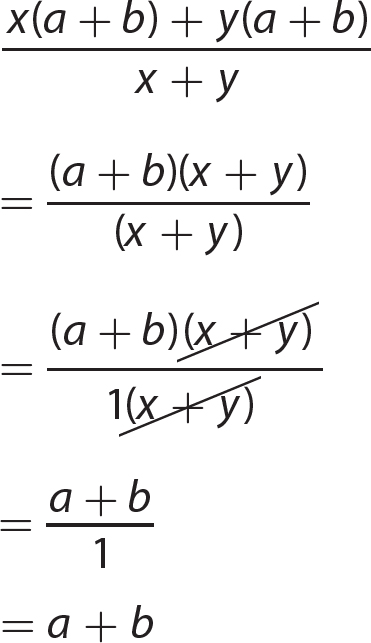
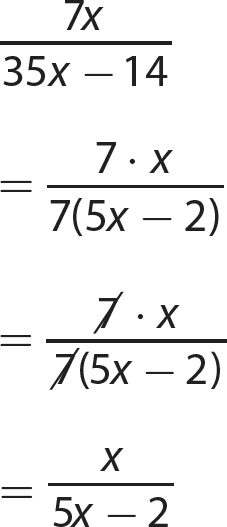
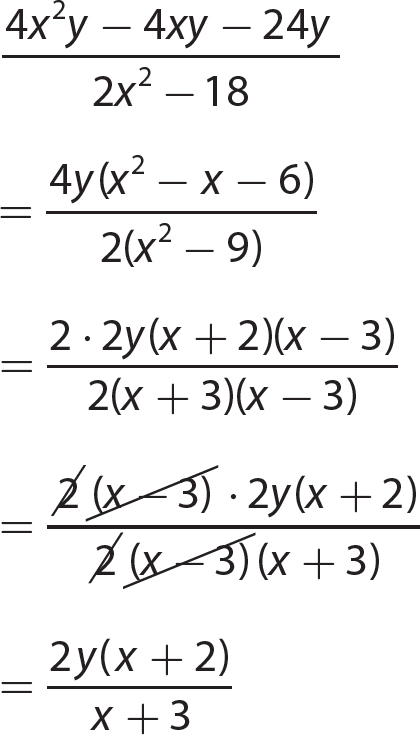
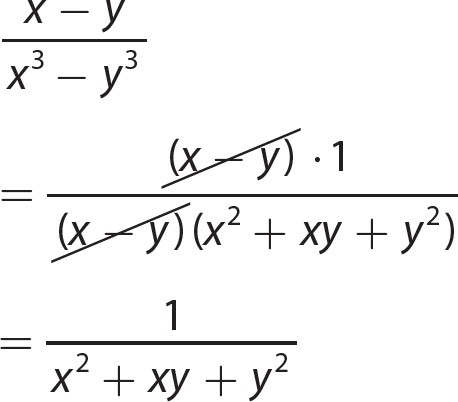
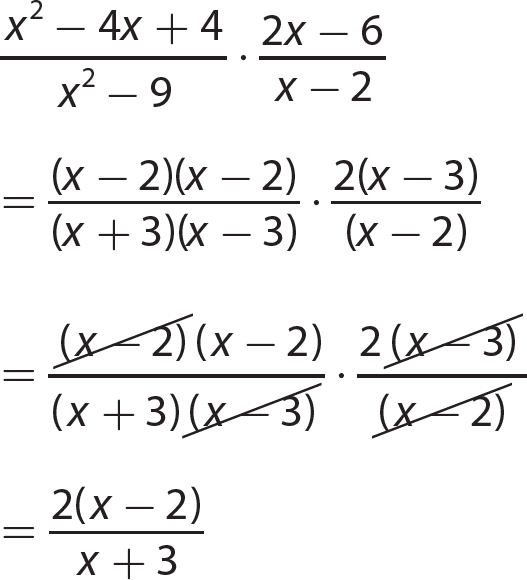
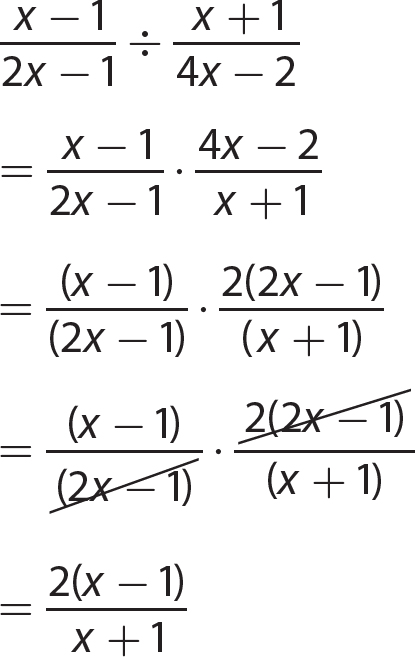
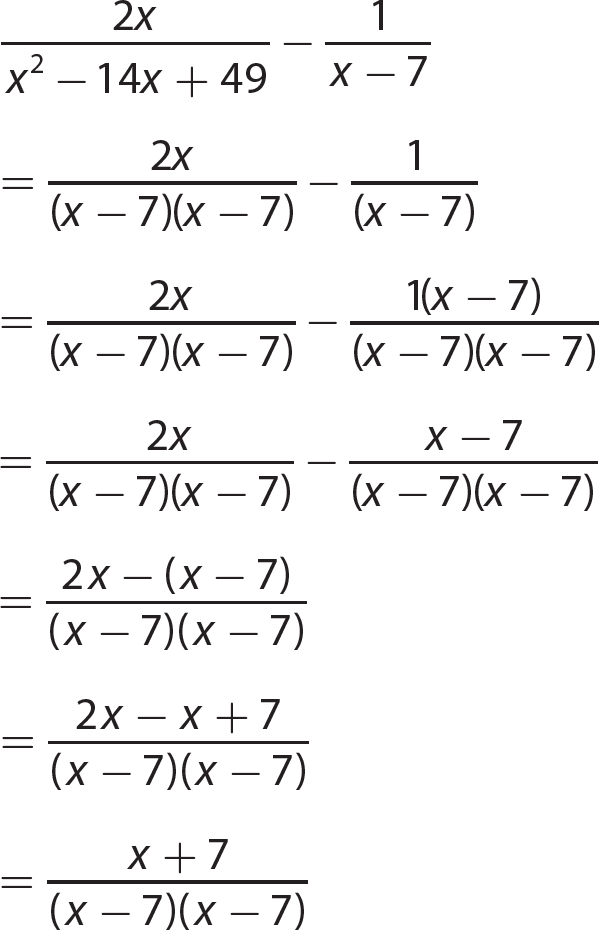
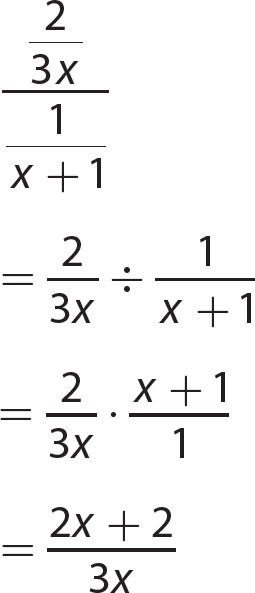
Chapter 14 Solving Linear Equations and Inequalities
Exercise 14
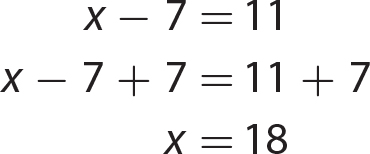
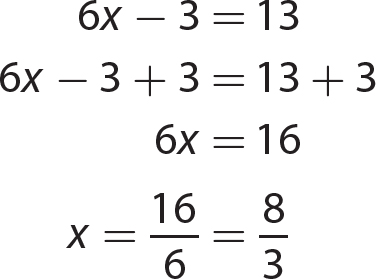
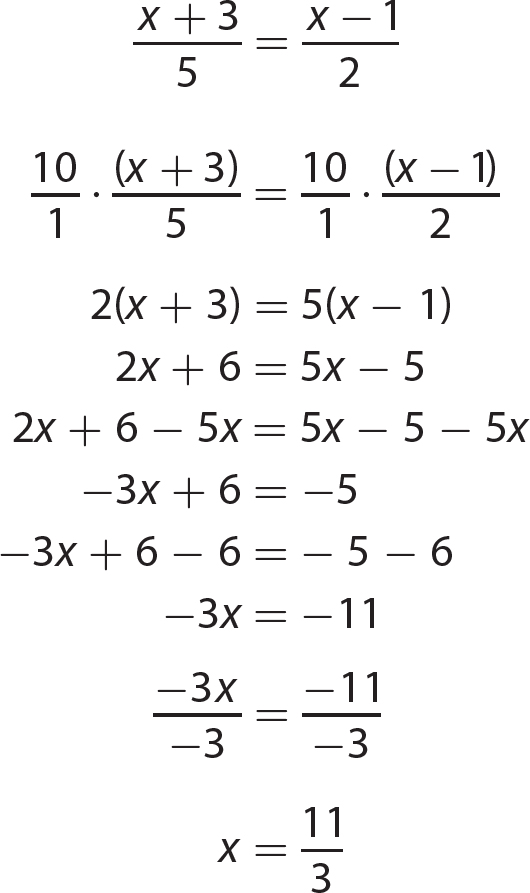
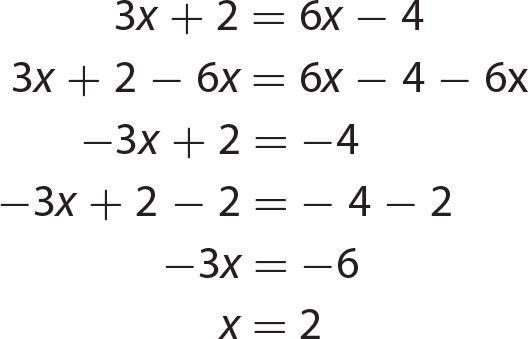
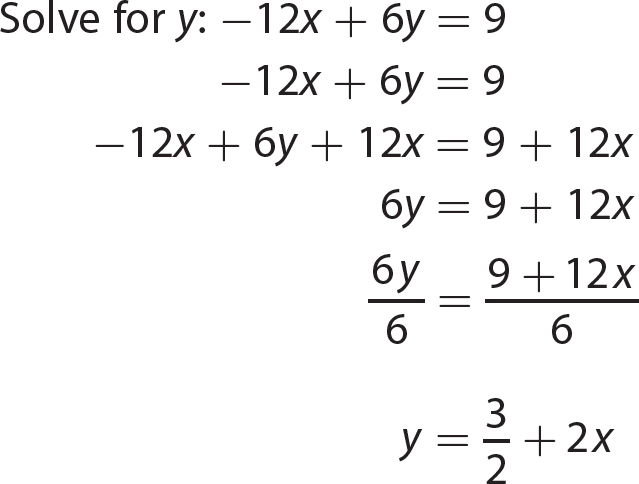
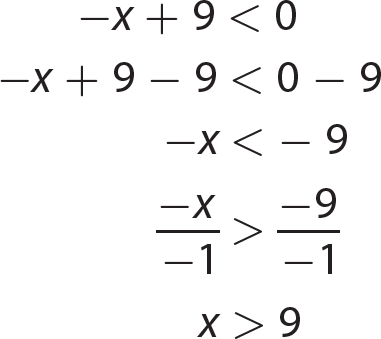
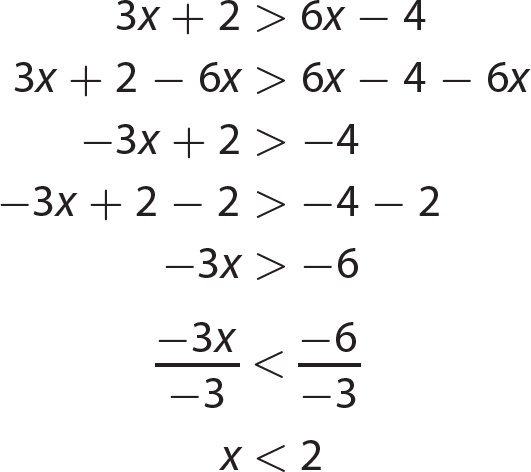
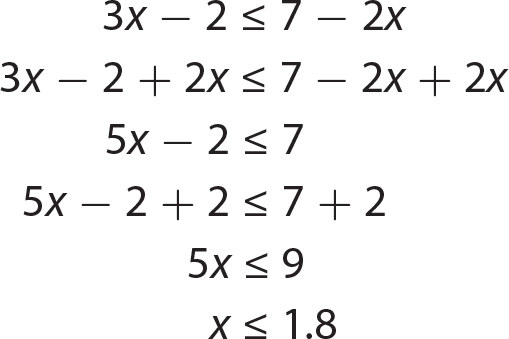
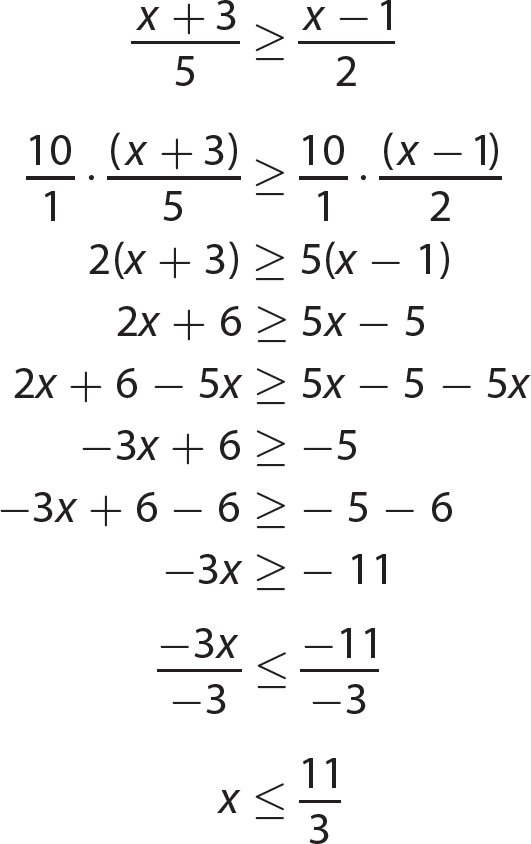
Chapter 15 Solving Quadratic Equations
Exercise 15
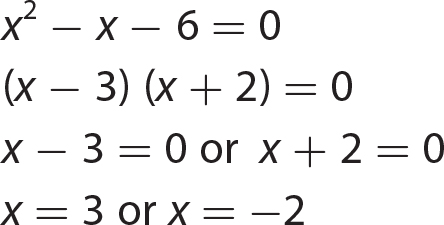
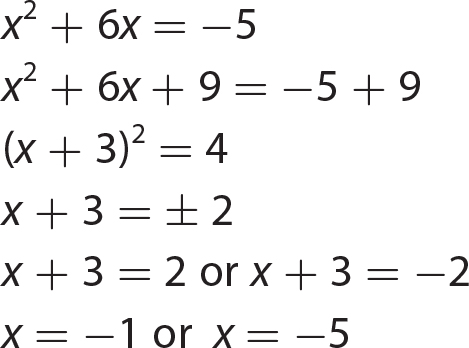
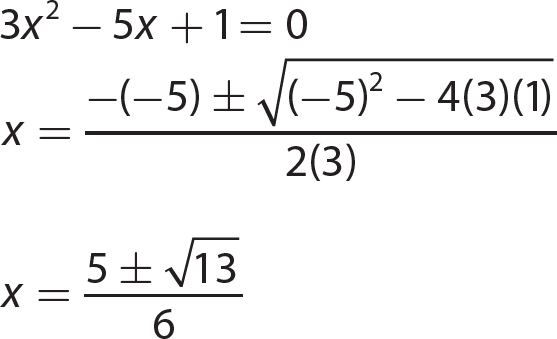
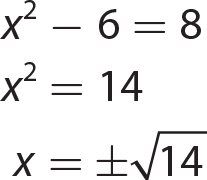
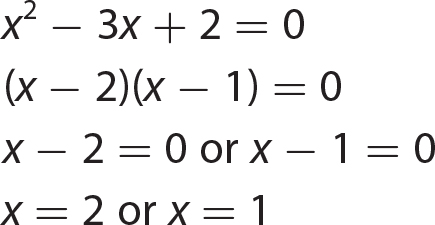
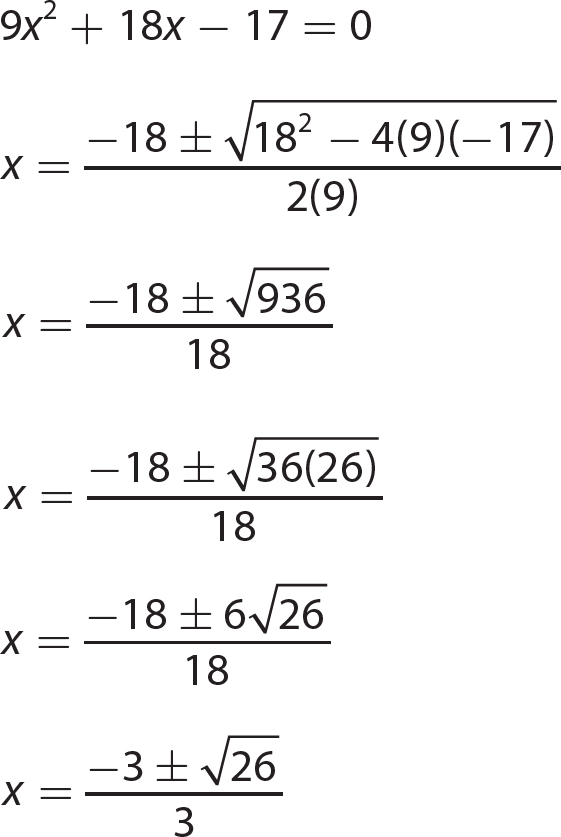
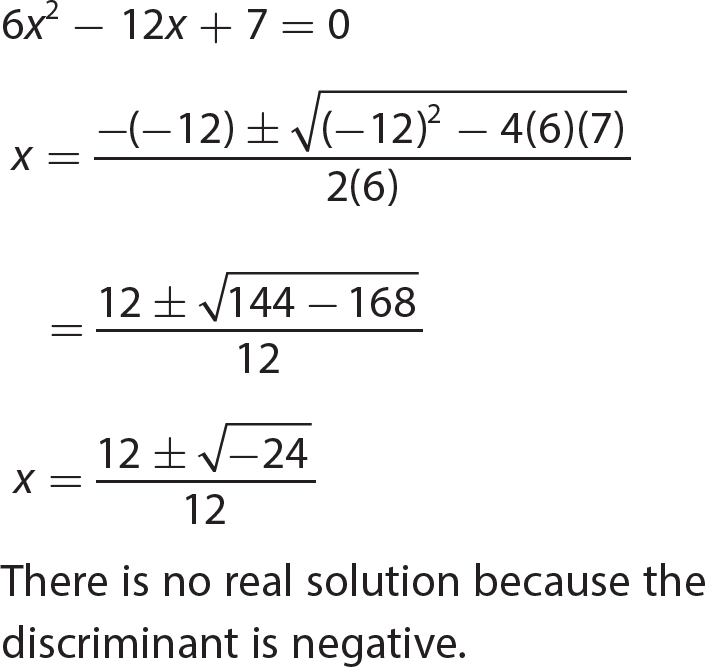
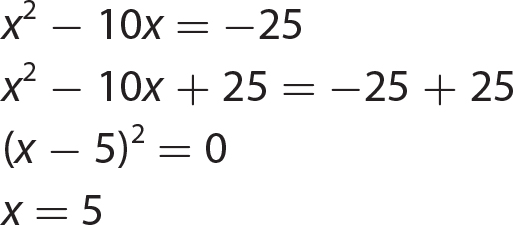
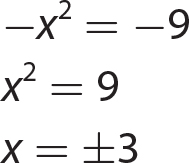
Chapter 16 The Cartesian Coordinate Plane
Exercise 16
1. True
2. False
3. True
4. False
5. True
6. False
7. rise
8. run
9. negative
10. positive
11. zero
13. −
14. undefined
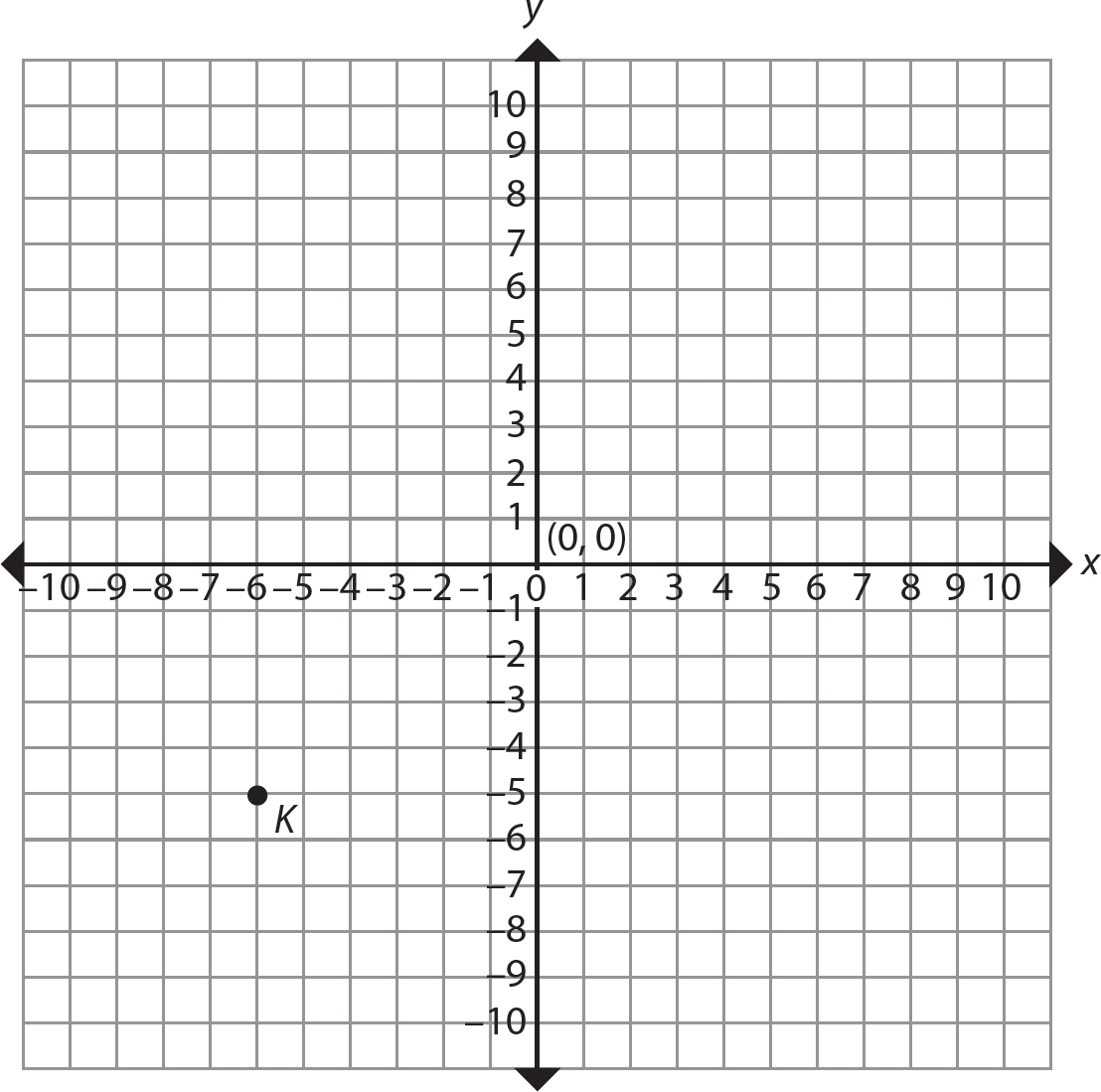
The point K is 6 units to the left of the y-axis and 5 units below the x-axis, so (− 6, − 5) is the ordered pair corresponding to point K.
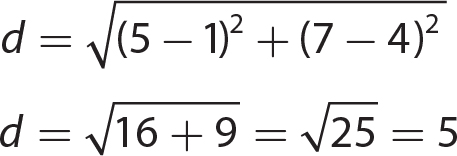
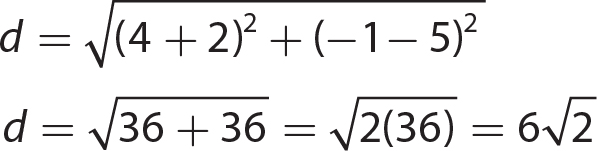
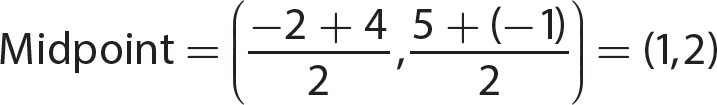
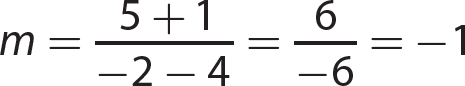
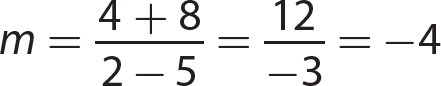
Chapter 17 Graphing Linear Equations
Exercise 17
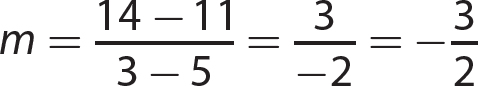
2. y = − 2x + 6
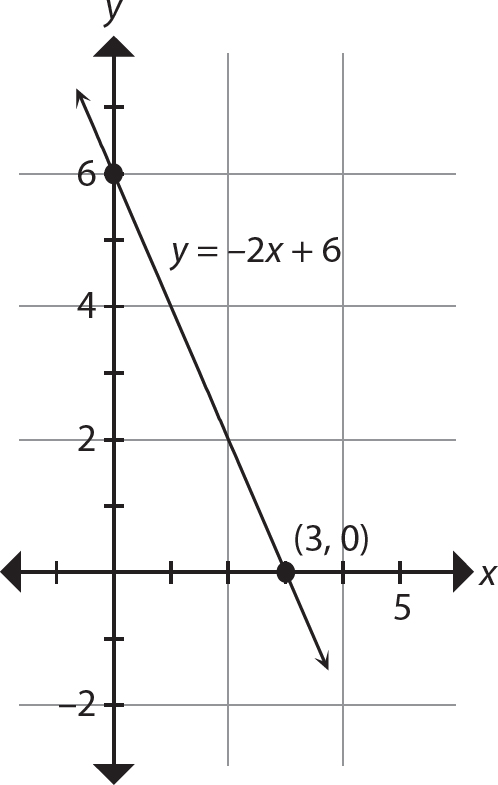
3. 3y = 5x − 9
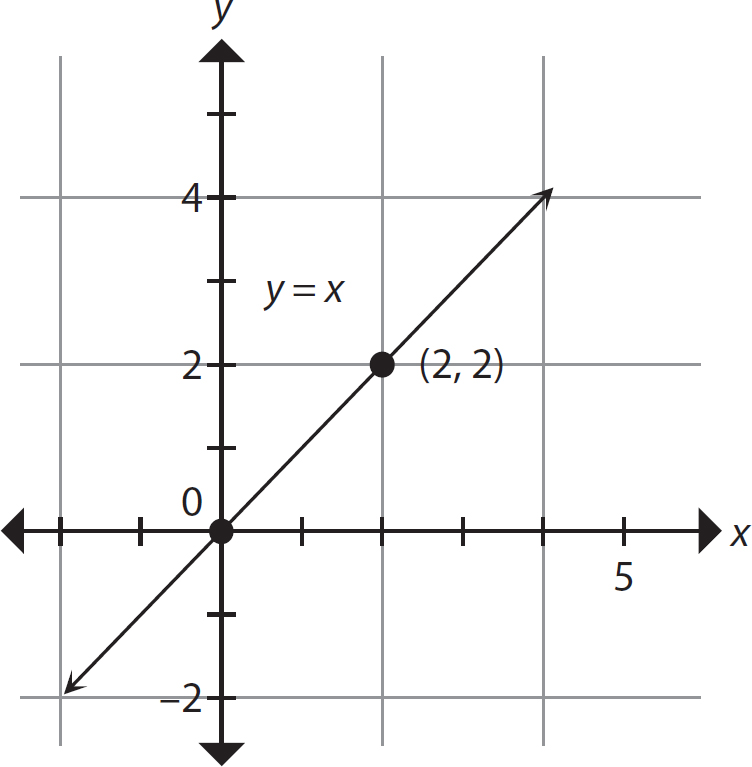
4. y = x
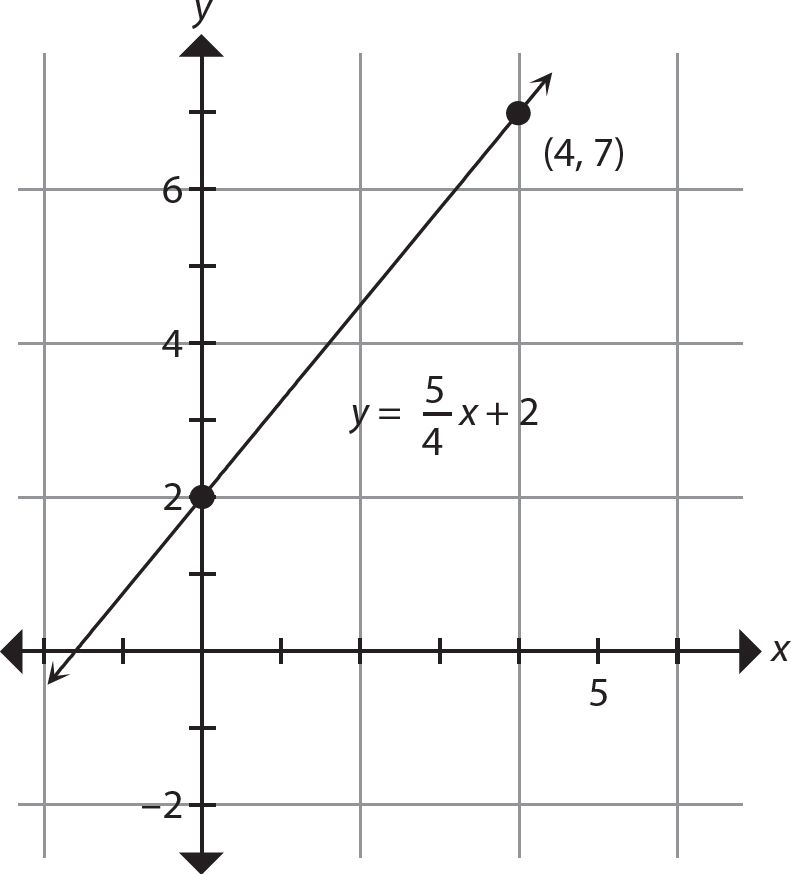
5. 4y − 5x = 8
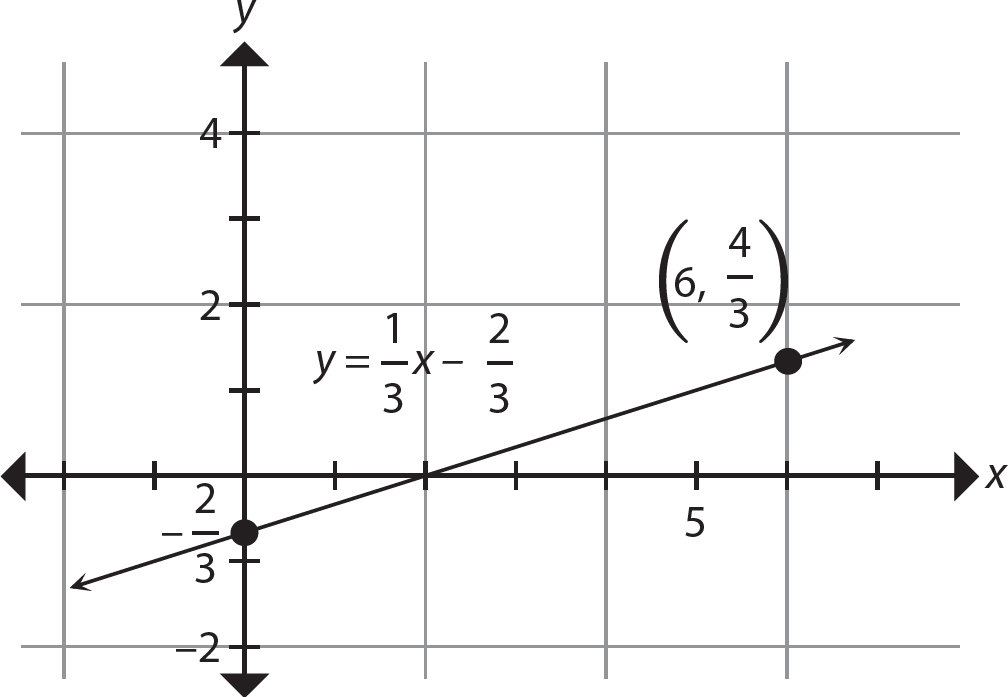
Chapter 18 The Equation of a Line
Exercise 18
1. y = 4x + 3
2. y = − 3x − 3
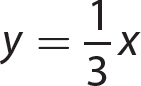
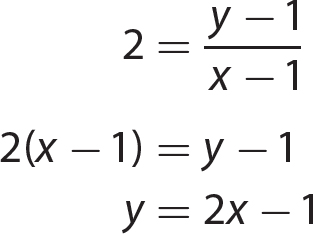
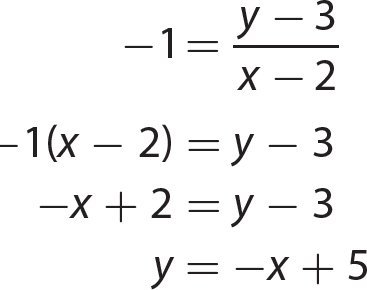
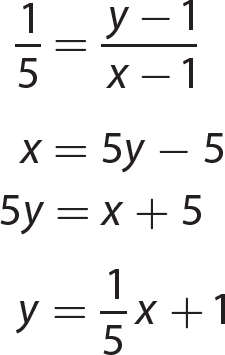
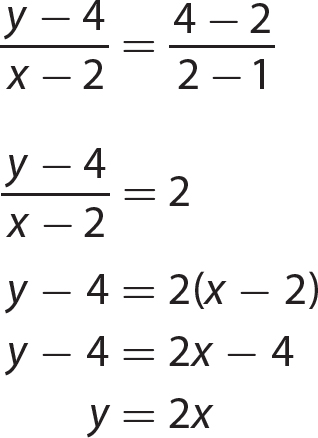
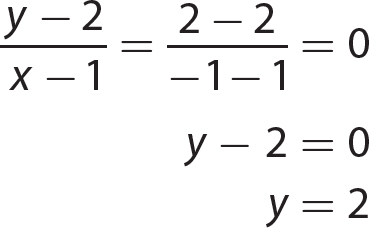
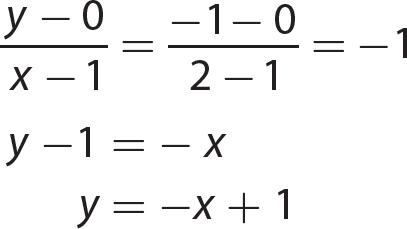
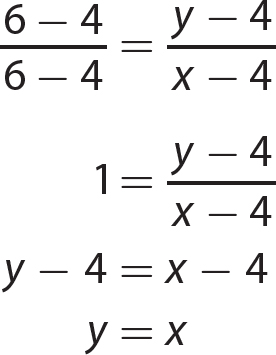
Chapter 19 Basic Function Concepts
Exercise 19
1. a. f = {(2, 1), (4, 5), (6, 9), (5, 9)}
b. g = {(3, 4), (5, 1), (6, 3), (3, 6)}
c. h = {(2, 1)}
d. t = {(7, 5), (8, 9), (8, 9)}
Only f, h, and t are functions. Note that in t, (8, 9) and (8, 9) are the same point.
2. The domain is {4, 6, 7, 8} and the range is {5, 7, 9}.
3. a. y = f(x) = 5x − 7. The domain is the set of all real numbers.
b.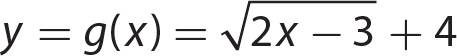 
Set 2x − 3 ≥ 0 and solve.
2x − 3 ≥ 0
2x ≥ 3
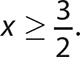The domain is the set of all real numbers greater than or equal to 
.
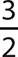c.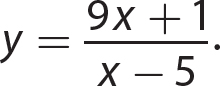 
The domain is the set of all real numbers except 5.
d.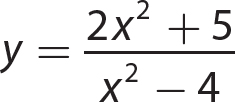 
Set x2 − 4 = 0 and solve.
x = ±2. The domain is the set of all real numbers except 2 and − 2.
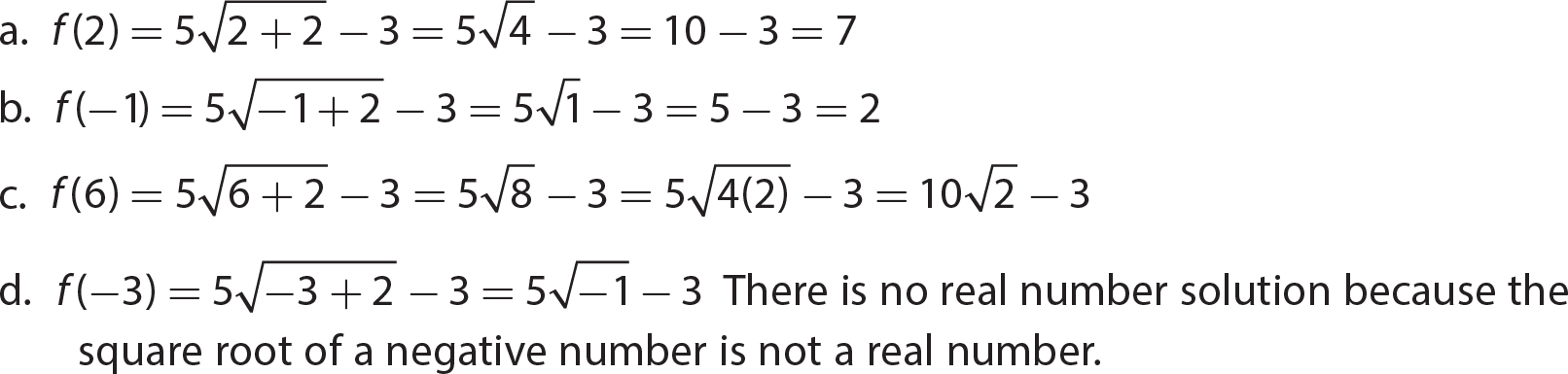
5. Only graphs b and c are functions.
6. y = 4x + 1
Chapter 20 Systems of Equations
Exercise 20
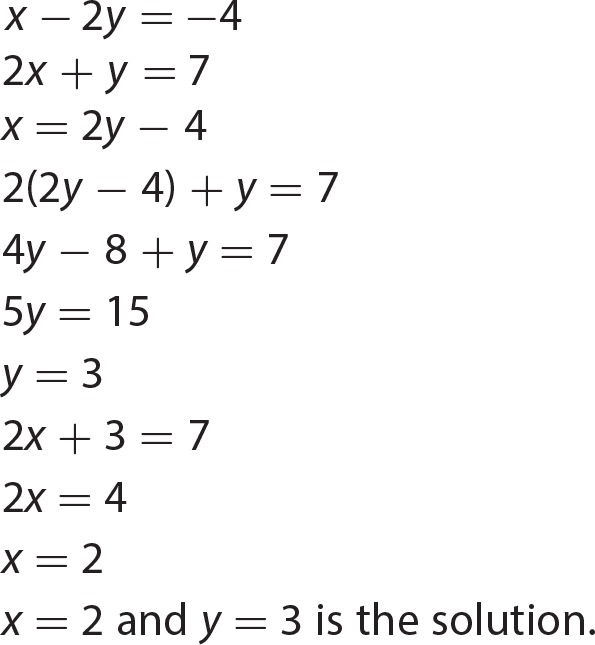
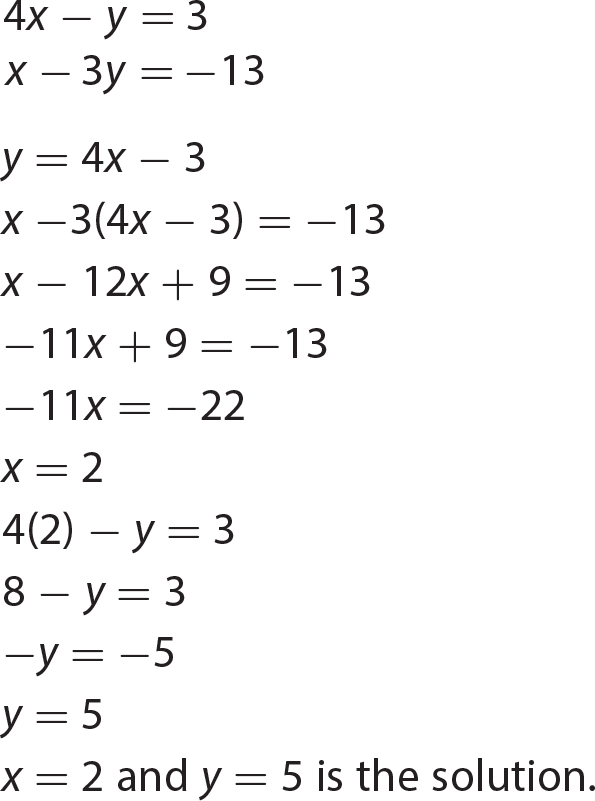
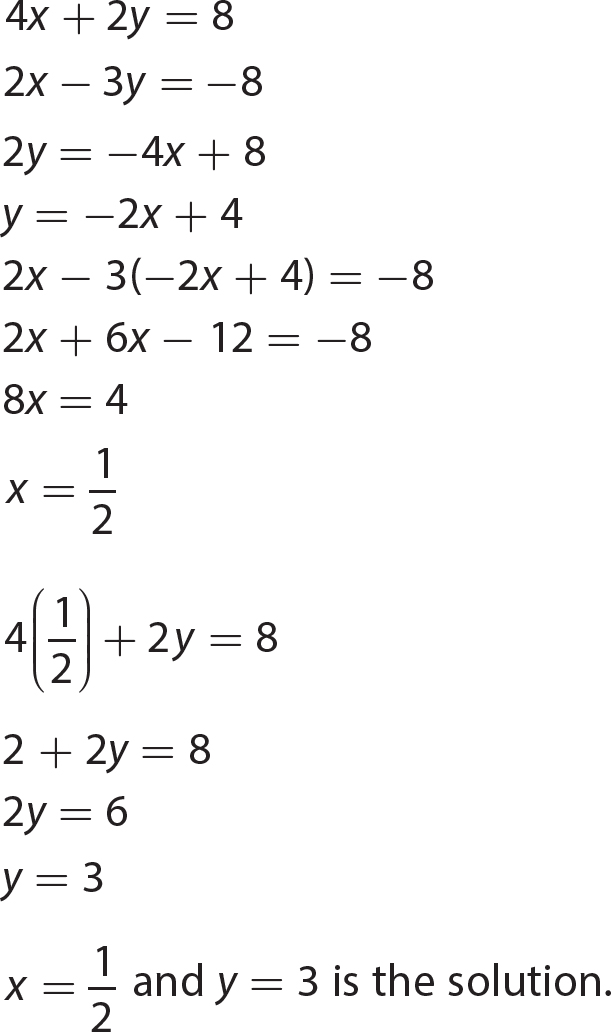
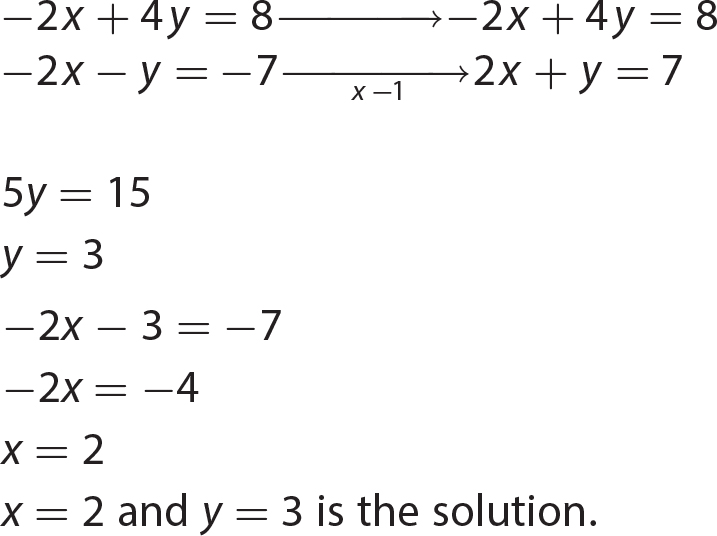
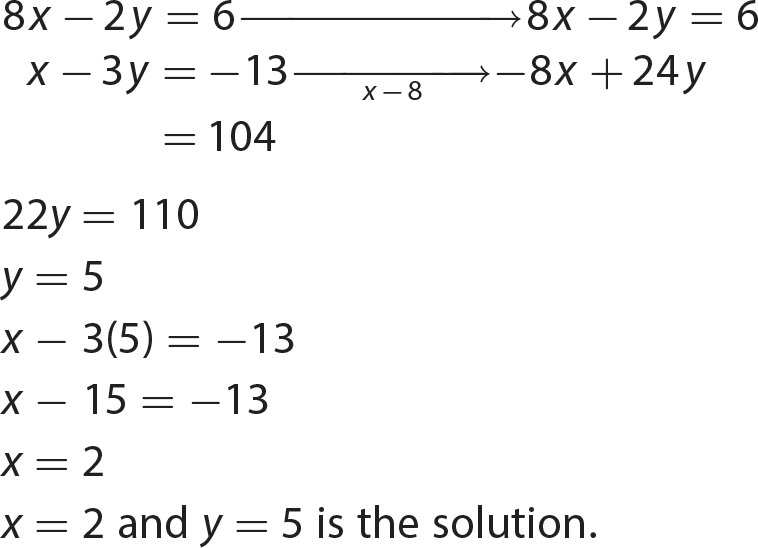
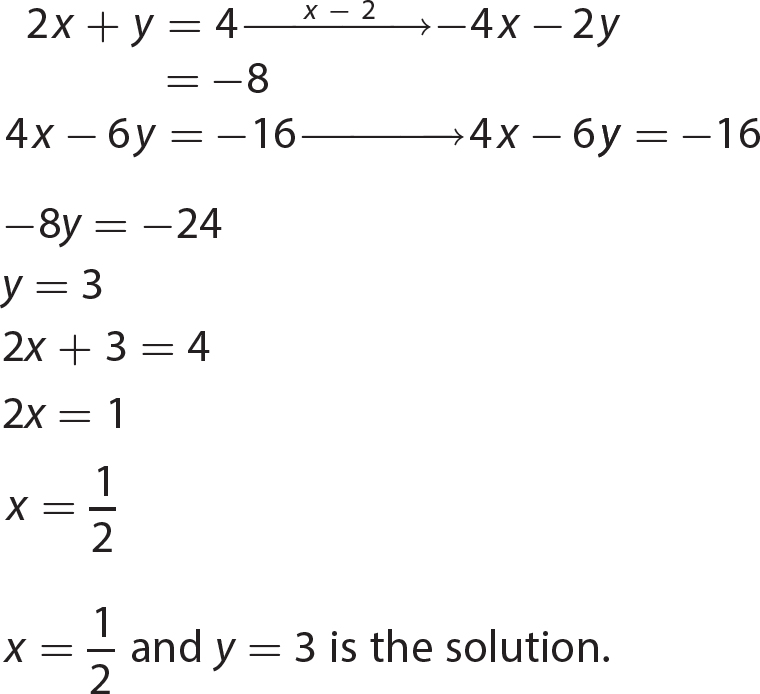
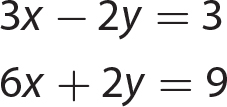
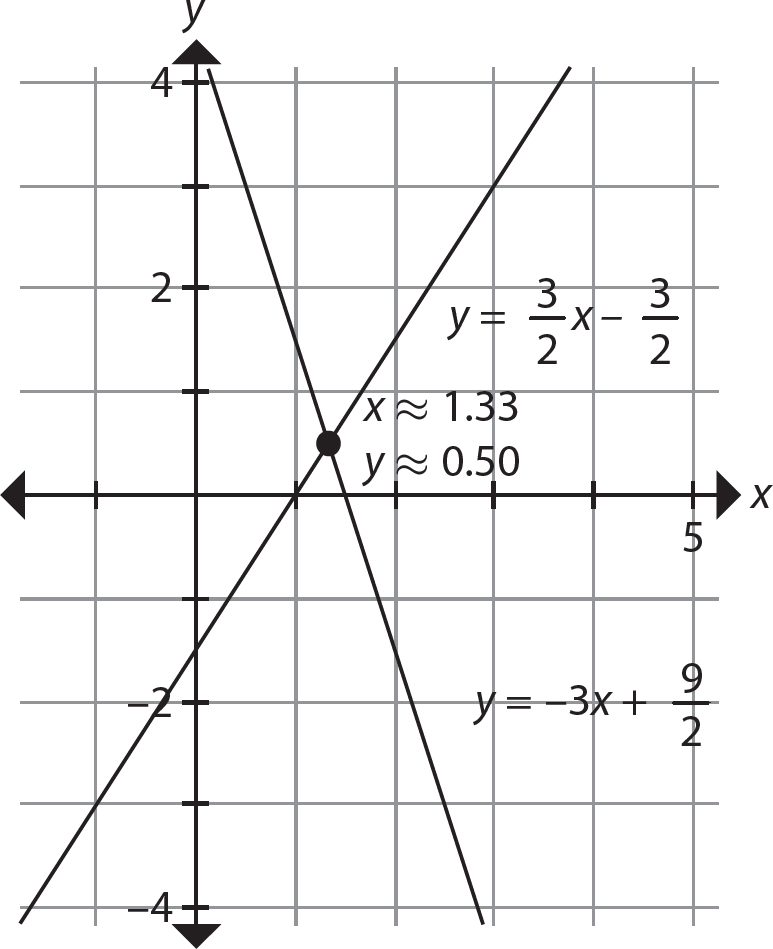
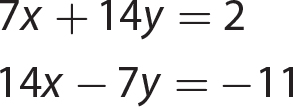
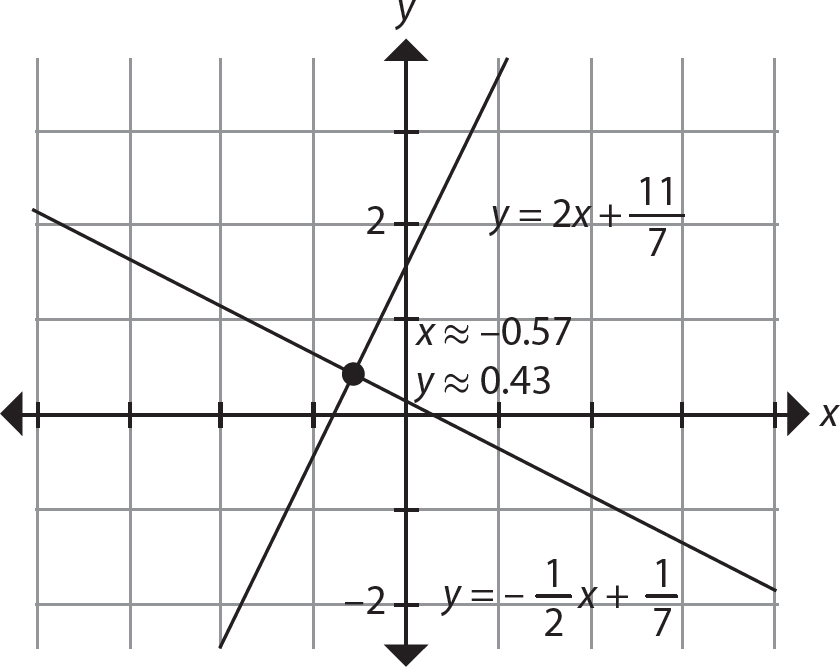
Chapter 21 Signal Words and Phrases
Exercise 21
1. 80x + 500
2. 125 + 40%x
3. P − 2w
4. 100 − K
5. 420 − 5y
6. (50x)(20)
11. 6%B = 57.60.
12. 0.25x + 0.10(42 − x) = 5.55.
13. 55t + 65t = 624.
14. c2 = 82 + 152.
15. 
.
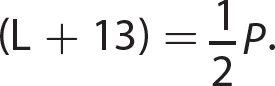Chapter 22 Word Problems
Exercise 22
1. This is an age relationships problem. Let N = Nidhi’s age (in years) and 4N = Nidhi’s grandmother’s age (in years).
Solve the equation.
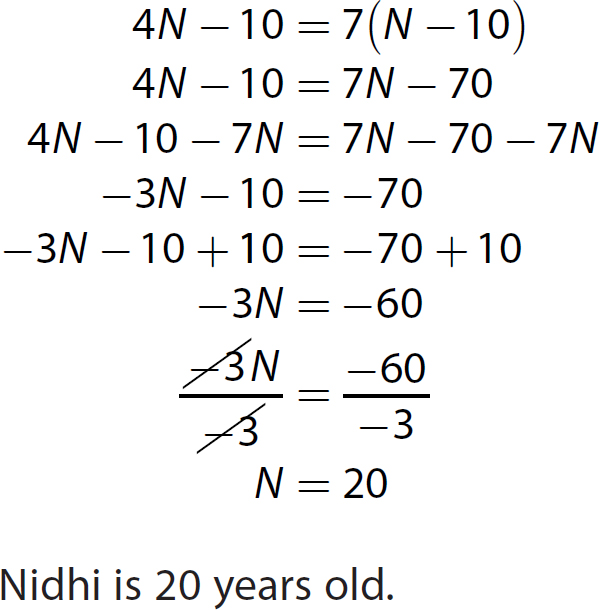
2. This is a consecutive integers problem. Let n = the first integer, n + 1 = the second integer, and n + 2 = the third integer.
Solve the equation.
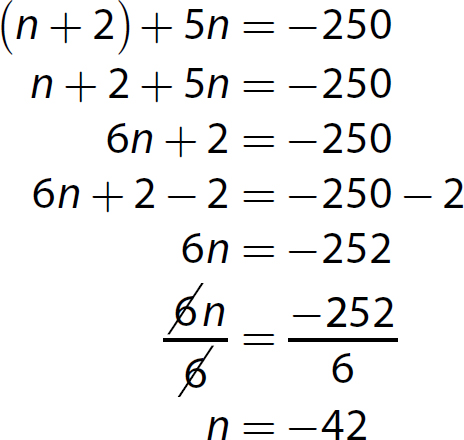
Find (n + 2), the greatest integer.
n + 2 = −42 + 2 = −40.
The greatest of the three integers is −40.
3. This is a consecutive even integers problem. Let n = the first even integer, n + 2 = the second even integer, and n + 4 = the third even integer.
Solve the equation.
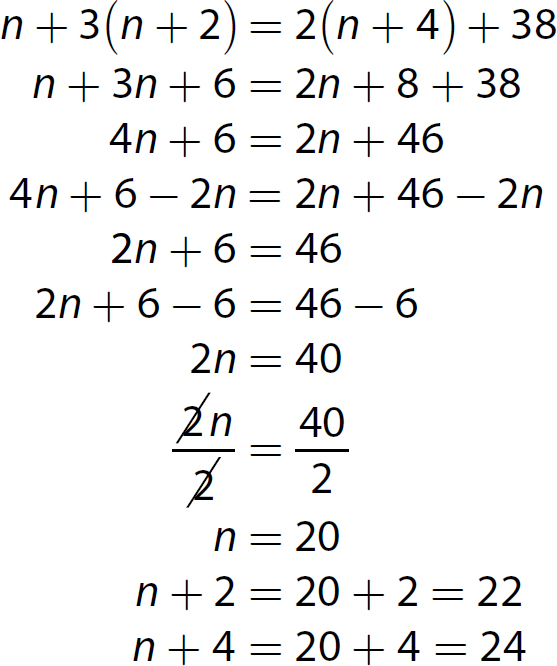
The three even integers are 20, 22, and 24.
4. This is a ratio problem. Let 4x = the number of women in the organization and 5x = the number of men in the organization.
Solve the equation.
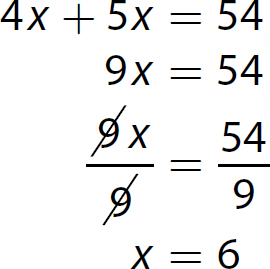
Find 4x, the number of women in the organization.
4x = 24
There are 24 women in the organization.
5. This is a mixture problem. Let W = the amount (in milliliters) of distilled water to be added and W + 1000 = the amount (in milliliters) of the final 50% alcohol solution.
Solve the equation. Note: Distilled water contains 0% alcohol.
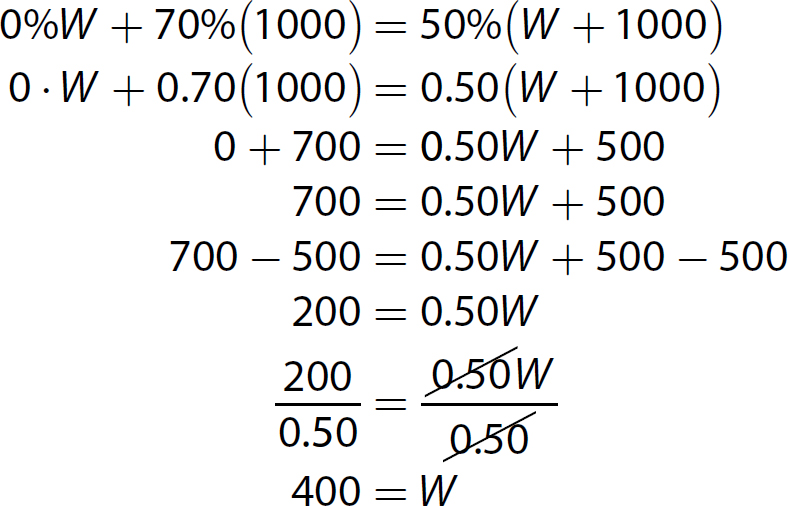
400 milliliters of distilled water must be added.
6. This is a mixture problem. Let x = the amount (in pounds) of the $10.50 coffee in the blend and y = the amount (in pounds) of the $8.50 coffee in the blend.
Solve the equations.
(1) x + y = 80
(2) 10.50x = 8.50y = 9(80)
Using the method of substitution, solve equation (1) for y in terms of x.
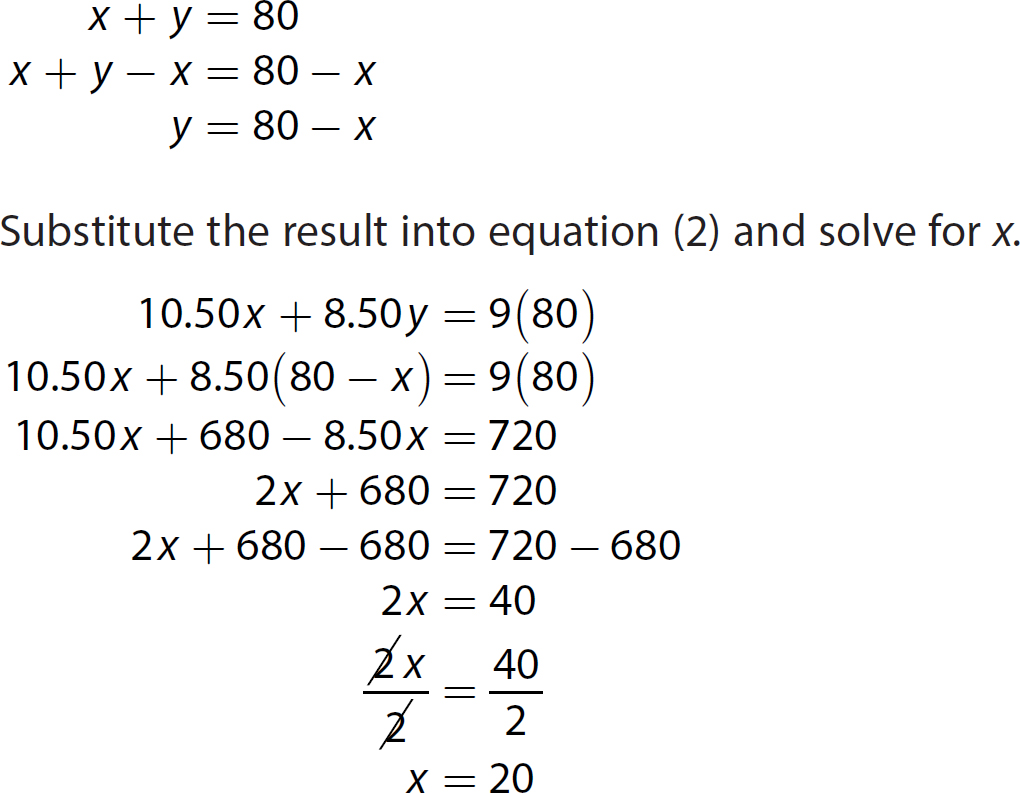
The owner should use 20 pounds of the $10.50 coffee in the blend.
7. This is a coins problem. Let n = the number of nickels in the collection and d = the number of dimes in the collection.
Solve the equations.
(1) n + d = 200
(2) 0.05n + 0.10d = 13.50
Using the method of substitution, solve equation (1) for n in terms of d.
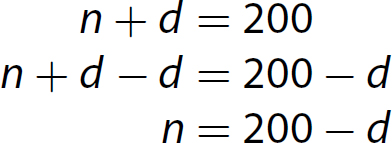
Substitute the result into equation (2) and solve for d.
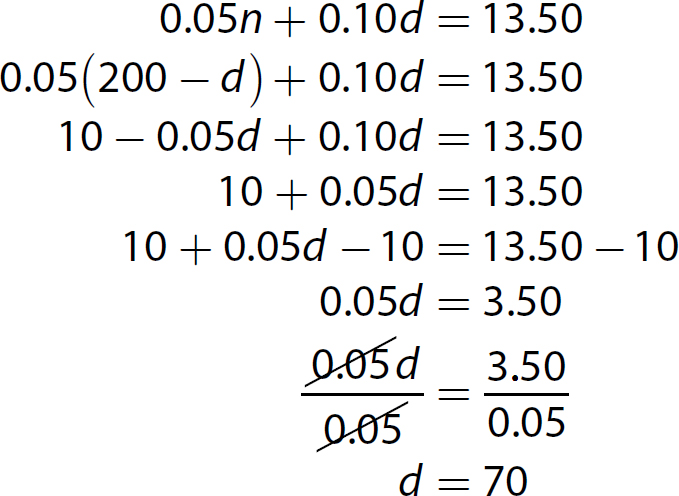
There are 70 dimes in the collection.
8. This is a rate-time-distance problem. Let t = the time (in hours) it will take the two vehicles to arrive at the same location.
Solve the equation.
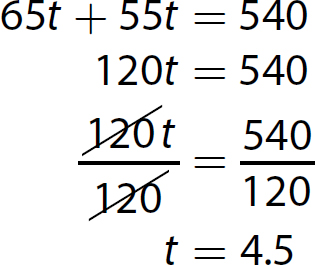
The two vehicles will arrive at the same location in 4.5 hours.
9. This is a work problem. Let t = the time (in hours) it will take the two pipes together to fill the tank.
Solve the equation.
The time it will take the two pipes together to fill the tank is 1.875 hours.
10. This is a percentage problem. The formula P = RB applies. P is unknown, R = 15%, and B = $295.
Solve the equation.
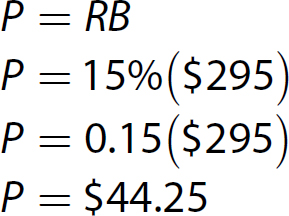
The amount saved is $44.25.
11. This is a percentage problem. The formula P = RB applies. B is unknown, R = 3%, and P = $55.35.
Solve the equation.
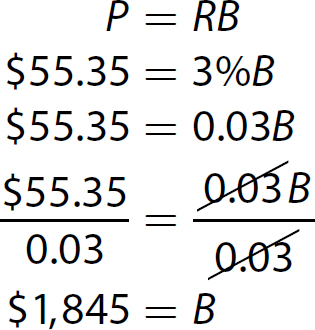
Last week, Ash’s total sales were $1,845.
12. This is a percentage problem. The formula P = RB applies. R is unknown, P = $1,624, and B = $5,800.
Solve the equation.
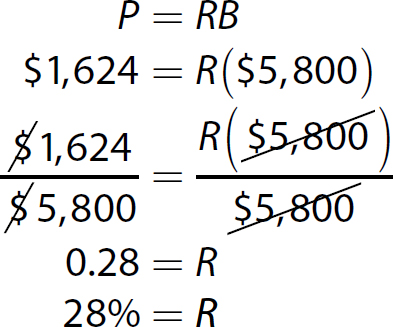
The amount saved is 28% of the original price.
13. This is a simple interest problem. The formula I = Prt applies. I is unknown, P = $15,000, r = 1.5% per year, and t = 8 years.
Solve the equation.
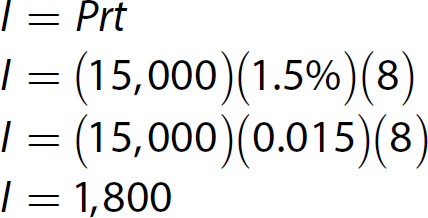
The investment will earn $1,800 in interest.
14. This is a number relationships problem. Let n = the second number and 2n + 12 = the first number.
Solve the equation.
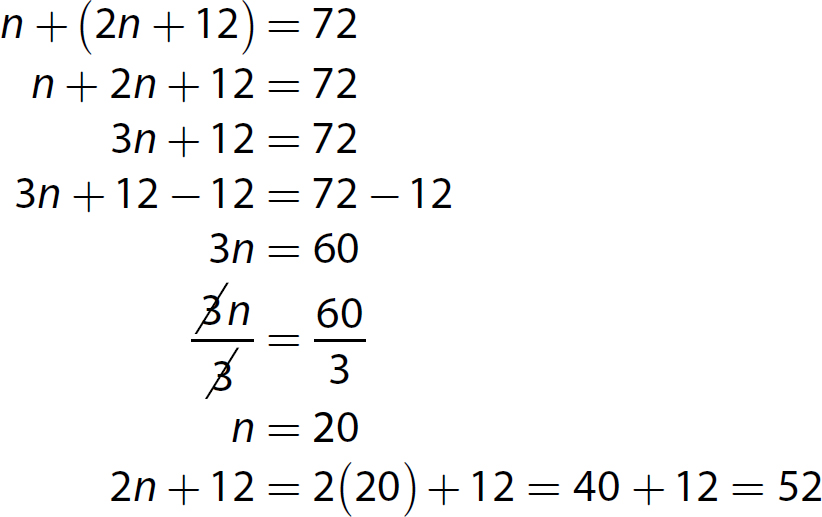
The two numbers are 20 and 52.
15. This problem involves the area of a rectangular geometric shape. Let W = the fence’s width (in meters) and 2W = the fence’s length (in meters).
Solve the equation.
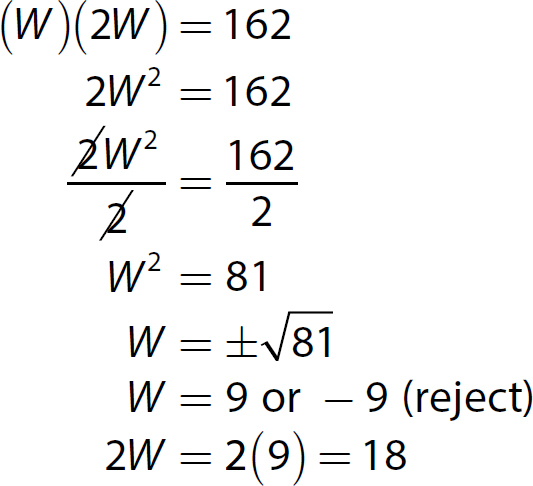
The fence’s width is 9 meters and its length is 18 meters.