Representations of a Function
Basic function concepts are presented in this chapter. One of the fundamental concepts of mathematics is the notion of a function. In algebra, you will see this idea in various settings, and you should become familiar with the different representations (forms) of a function. Three of the most frequently used representations are presented here.
Form 1: Ordered Pairs
A function is a set of ordered pairs such that no two different ordered pairs have the same first coordinate. The domain of a function is the set of all first coordinates of the ordered pairs in the function. The range of a function is the set of all second coordinates of the ordered pairs in the function.
Problem Determine which of the two sets is a function and identify the domain and range of the function.
f = {(4, 1), (3, 7), (2, 5), (5, 5)} w = {(5, 1), (4, 3), (6, 3), (4, 2)}
Solution
Step 1. Analyze the sets for ordered pairs that satisfy the function criteria. Set f is a function because no ordered pairs have the same first coordinate. Set w is not a function because (4, 3) and (4, 2) have the same first coordinate, but different second coordinates.
Step 2. Isolate the first and second coordinates of the function f.
The domain of f is D = { 2, 3, 4, 5 } and the range of f is R = { 1, 5, 7 }.
Problem Identify the domain and range of the function g = {(1,2), (2, 3), (3, 4), (4, 5),…}.
Solution
Step 1. Isolate the first and second coordinates of g.
The domain of g is D = {1, 2, 3, 4, …}, and the range of g is R = {2, 3, 4, 5, …}.
Form 2: Equation or Rule
The ordered pair form is very useful for getting across the basic idea, but other forms are more useful for algebraic work.
A function is a rule of correspondence between two sets A and B such that each element in set A is paired with exactly one element in set B. In algebra, the rule is normally an equation in two variables. An example is the equation y = 3x + 7. For this rule, 1 is paired with 10, 2 with 13, and 5 with 22. This is equivalent to saying that the ordered pairs (1, 10), (2, 13) and (5, 22) are in the function.
If the domain of a function is not obvious or not specified, then it is generally assumed that the domain is the largest set of real numbers for which the equation has numerical meaning in the set of real numbers. The domain, then, unless otherwise stated, is all the real numbers except excluded values. To determine the domain, start with the real numbers and exclude all values for x, if any, that would make the equation undefined over the real numbers.
Problem State the domain of the given function.
a.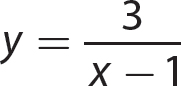 
b.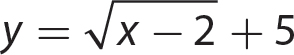 
Solution
a.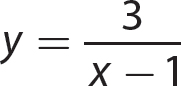
Step 1. Set the denominator equal to 0 and solve for x.
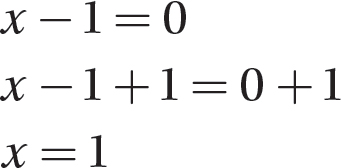
Step 2. State the domain.
The domain of 
is all real numbers except 1.
b.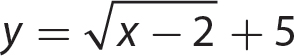 
Step 1. Because the square root is an even root, set the term under the radical greater than or equal to 0 and solve the inequality.
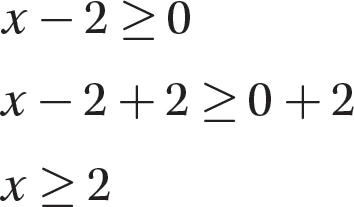
Step 2. State the domain.
The domain of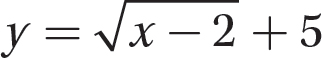 
is all real numbers greater than or equal to 2.
Terminology of Functions
A function is completely determined when the domain is known and the rule is specified. Even though the range is determined, it is often difficult to exhibit or specify the set of numbers in the range. Some of the techniques for determining the range of a function are beyond the scope of this book, and the focus here will be mostly on the domain and the equation that gives the rule. In fact, the words rule and equation will be used synonymously.
Some common terminology used in the study of functions is the following: (1) Domain values are inputs, and range values are outputs. (2) In equations of the form y = 3x + 5, x is the independent variable, and y is the dependent variable. Also, a convenient notation for a function is to use the symbol f(x) to denote the value of the function f at a given value for x. In this setting, it is convenient to think of x as being an input value and f(x) as being an output value. You can also write the function y = 3x + 5 as f(x) = 3x + 5, where y = f(x).
Problem Find the value of the function f(x) = 3x + 5 at the given x value.
a. x = 3
b. x = 0
Solution
a. x = 3
Step 1. Check whether 3 is in the domain of the function.
The equation will generate real number values for each real number x. The domain, then, is all real numbers. Thus, 3 is in the domain of f.
Step 2. Substitute the given number for x in the equation and evaluate.
f(3) = 3(3) + 5
f(3) = 14
b. x = 0
Step 1. Check whether 0 is in the domain of the function.
The equation will generate real number values for each real number x. The domain, then, is all real numbers. Thus, 0 is in the domain of f.
Step 2. Substitute the given number for x in the equation and evaluate.
f(0) = 3(0) + 5
f(0) = 5
Problem Find the value of the function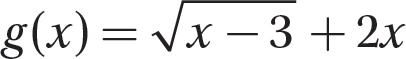 
at the given x value.
a. x = 4
b. x = 1
c. x = 8
Solution
a. x = 4
Step 1. Check whether 4 is in the domain of the function.
The square root of a negative number is not a real number, so set x−3 ≥ 0 and solve the inequality to determine the domain of the function.
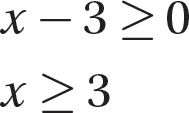
The domain is all real numbers greater than or equal to 3. Thus, 4 is in the domain of g.
Step 2. Substitute 4 for x in the equation and evaluate.
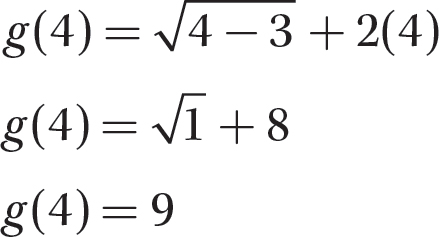
b. x = 1
Step 1. Check whether 1 is in the domain of the function.
The square root of a negative number is not a real number, so set x – 3 ≥ 0 and solve the inequality to determine the domain of the function.
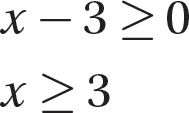
The domain is all real numbers greater than or equal to 3. Thus, 1 is not in the domain of g, so the function has no value at 1.
c. x = 8
Step 1. Check whether 8 is in the domain of the function.
The square root of a negative number is not a real number, so set x – 3 ≥ 0 and solve the inequality to determine the domain of the function.
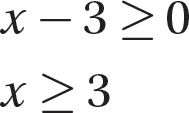
The domain is all real numbers greater than or equal to 3. Thus, 8 is in the domain of g.
Step 2. Substitute 8 for x in the equation and evaluate.
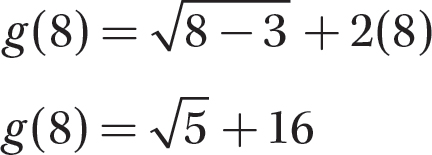
Problem Find the value of the function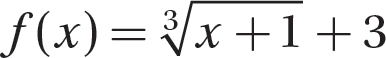 
at the given x value.
a. x = −9
b. x = 0
Solution
a. x = −9
Step 1. Check whether −9 is in the domain of the function.
Because the cube root is an odd root number, there is no restriction on the values under the radical. The domain, then, is all real numbers, so −9 is in the domain of f.
Step 2. Substitute −9 for x in the equation and evaluate.
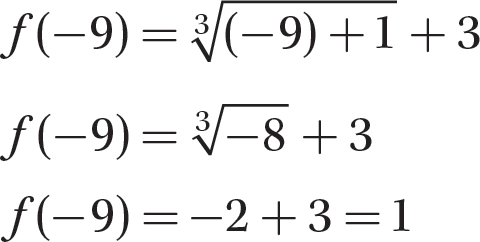
b. x = 0
Step 1. Check whether 0 is in the domain of the function.
Because the cube root is defined for all real numbers, there is no restriction on the values under the radical. The domain, then, is all real numbers, so 0 is in the domain of f.
Step 2. Substitute 0 for x in the equation and evaluate.
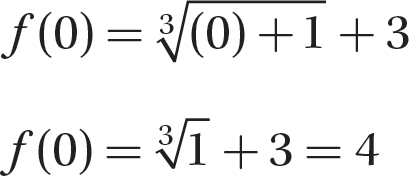
Form 3: Graphical Representation
An additional way to represent a function is by graphing the function in the Cartesian coordinate plane. You can easily determine whether a graph is the graph of a function by using the vertical line test. A graph is the graph of a function if and only if no vertical line crosses the graph in more than one point. This is a quick visual determination and is the graphical equivalent of saying that no two different ordered pairs have the same first coordinate.
Problem Determine which of the following is the graph of a function.
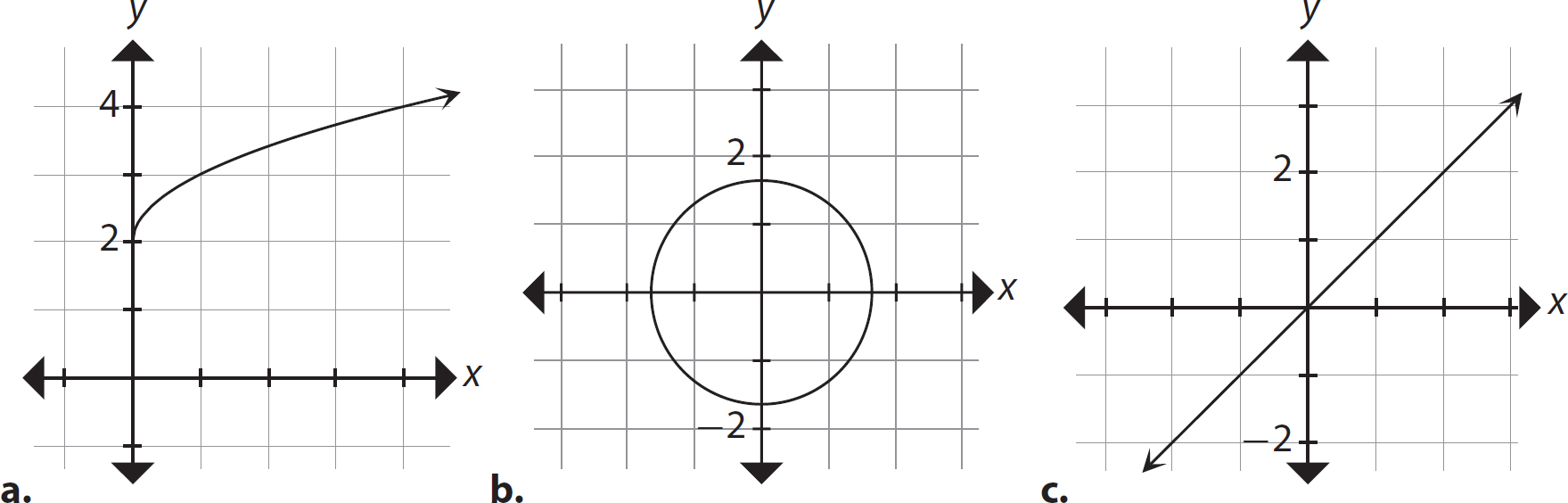
Solution
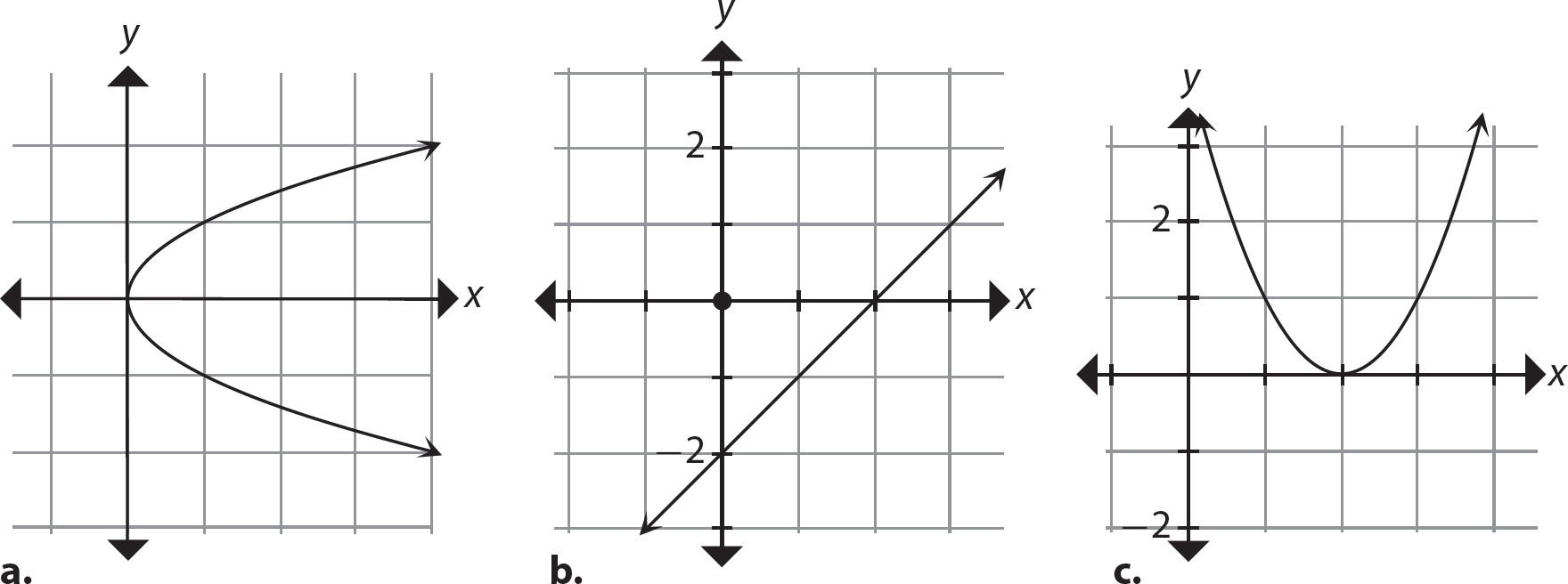
Step 1. Mentally apply the vertical line test to each graph.
a. This is the graph of a function.
b. This is not the graph of a function because a vertical line drawn through the point x = 1 will cross the graph in more than one point. (Actually, there are infinitely many vertical lines that will cross in more than one point, but it only takes one to ascertain it is not a function.)
c. This is the graph of a function.
Some Common Functions
Some of the more common functions you will study in algebra are listed here in general form and given special names.
a. y = f(x) = ax + bLinear function
b. y = f(x) = ax2 + bx + c, a ≠ 0Quadratic function
c. y = |x|Absolute value function
d. y =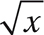 
Square root function
Chapter 17 dealt with the graph of linear functions. Sample graphs of the four functions above are shown in Figure 19.1. These are easily graphed with a graphing calculator, which is a good tool to have when you study algebra.
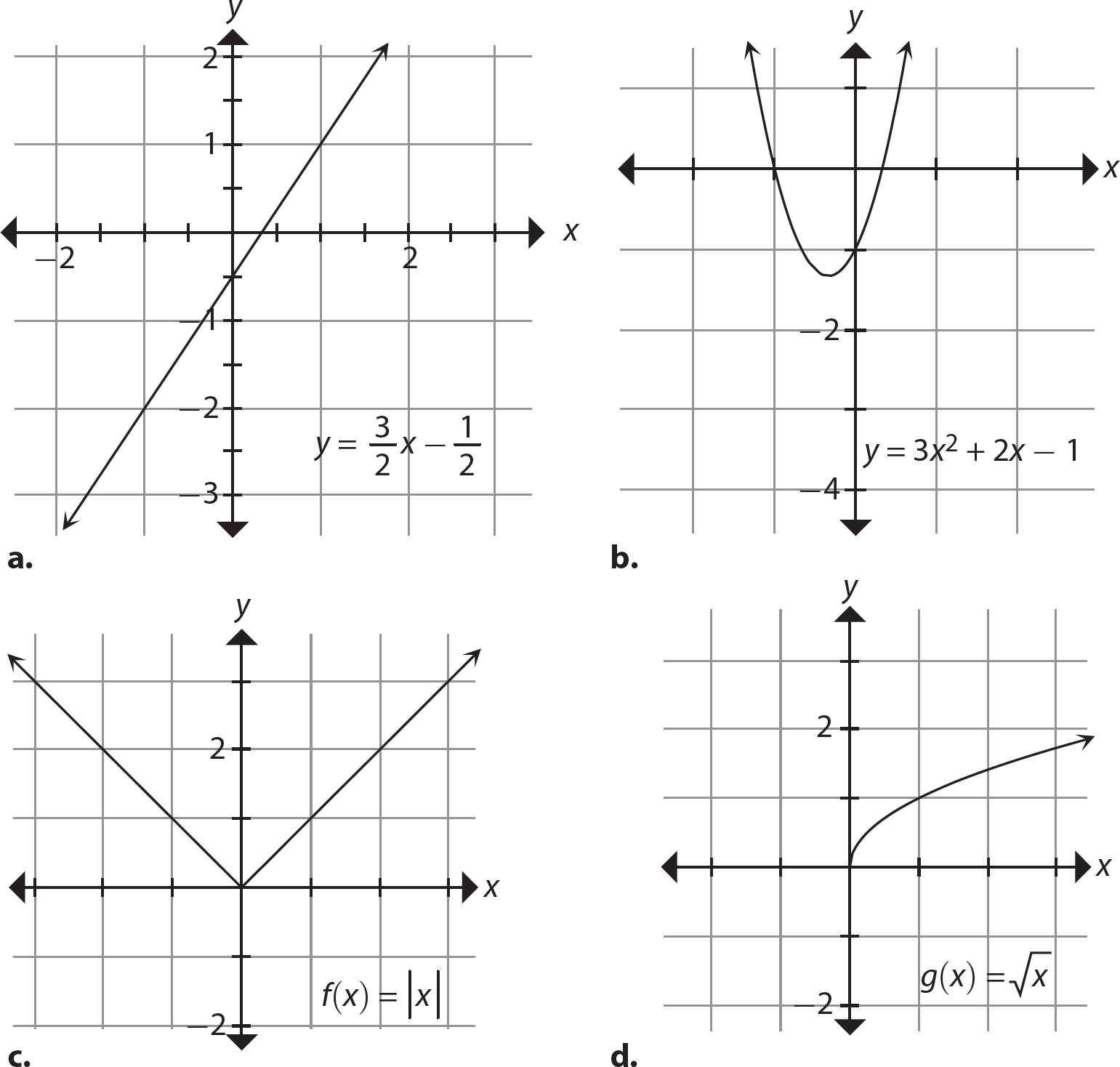
Figure 19.1 Sample graphs of four common functions: a) linear function; b) quadratic function; c) absolute value function; d) square root function
Of course, you can graph these functions “by hand” by setting up an x-y T-table and substituting several representative values for x.
Functional relationships naturally occur in many and various circumstances. A few examples will illustrate.
Problem Establish a functional relationship between the radius of a circle and its area.
Solution
Step 1. The formula for the area of a circle is πr2, where r is the radius.
Area = A = πr2
Step 2. Express the area of a circle as a function of its radius.
A(r) = πr2
Problem Establish a functional relationship between the x and y values in the following table.
Solution
Step 1. Look for a pattern that will connect the two numbers and describe the pattern in words.
The y number is twice the x number plus 1.
Step 2. Write the pattern for y in terms of x.
y = 2x + 1
Exercise 19
1. Determine which of the sets are functions.
a. f = {(2, 1), (4, 5), (6, 9), (5, 9)}
b. g = {(3, 4), (5, 1), (6, 3), (3, 6)}
c. h = {(2, 1)}
d. t = {(7, 5), (8, 9), (8, 9)}
2. State the domain and range of the function g = {(4, 5), (8, 9), (7, 7), (6, 7)}.
3. Find the domain of each of the functions.
a. y = f(x) = 5x − 7
b.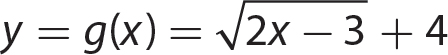 
c. 
d.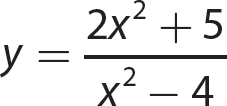 
4. If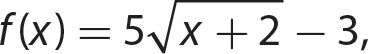 
, find the indicated value.
a. f(2)
b. f(−1)
c. f(6)
d. f(−3)
5. Which of the graphs is the graph of a function?
6. Write the equation for the functional relationship between x and y.
