9

Multiplying Polynomials

This chapter presents rules for multiplying polynomials. You use the properties of real numbers and the rules of exponents when you multiply polynomials.

Multiplying Monomials

Multiplying Monomials

To multiply monomials, (1) multiply the numerical coefficients, (2) multiply the variable factors using rules for exponents, and (3) use the product of the numerical coefficients as the coefficient of the product of the variable factors to obtain the answer.

Problem   Find the product.

a. (5x⁵y³)(3x²y⁶)

b. (−2a³b⁴)(8ab²)

c. (6x)(−2x)

d. (−10x³)(4x²)

e. (4x²y⁵)(−2xy³)(−3xy)

f. (x)(2)

Solution

a. (5x⁵y³)(3x²y⁶)

Step 1.   Multiply the numerical coefficients.

(5)(3) = 15

Step 2.   Multiply the variable factors.

(x⁵y³)(x²y⁶) = x⁷y⁹

To streamline your work when you are multiplying polynomials, arrange the variables in each term alphabetically.

Recall from Chapter 7 that when you multiply exponential expressions that have the same base, you add the exponents.

Step 3.   Use the product in step 1 as the coefficient of x⁷y⁹.

(5x⁵y³)(3x²y⁶) = 15x⁷y⁹

b. (−2a³b⁴)(8ab²)

Step 1.   Multiply the numerical coefficients.

(−2)(8) = −16

If no exponent is written on a variable, the exponent is understood to be 1.

Step 2.   Multiply the variable factors.

(a³b⁴)(ab²) = a⁴b⁶

Step 3.   Use the product in step 1 as the coefficient of a⁴b⁶.

(−2a³b⁴)(8ab²) = − 16a⁴b⁶

c. (6x)(−2x)

Step 1.   Multiply the numerical coefficients.

(6)(−2) = −12

Step 2.   Multiply the variable factors.

(x)(x) = x²

Step 3.   Use the product in step 1 as the coefficient of x².

(6x)(−2x) = −12x²

d. (−10x³)(4x²)

Step 1.   Multiply the numerical coefficients.

(−10)(4) = −40

Step 2.   Multiply the variable factors.

(x³)(x²) = x⁵

Step 3.   Use the product in step 1 as the coefficient of x⁵.

(−10x³)(4x²) = −40x⁵

e. (4x²y⁵)(−2xy³)(−3xy)

Step 1.   Multiply the numerical coefficients.

(4)(−2)(−3) = 24

Step 2.   Multiply the variable factors.

(x²y⁵)(xy³)(xy) = x⁴y⁹

Step 3.   Use the product in step 1 as the coefficient of x⁴y⁹.

(4x²y⁵)(−2xy³)(−3xy) = 24x⁴y⁹

f. (x)(2)

Step 1.   Multiply the numerical coefficients.

(1)(2) = 2

Step 2.   Multiply the variable factors.

There is only one variable factor, x.

Step 3.   Use the product in step 1 as the coefficient of x.

(x)(2) = 2x

Multiplying Polynomials by Monomials

Multiplying a Polynomial by a Monomial

To multiply a polynomial by a monomial, multiply each term of the polynomial by the monomial.

This rule is a direct application of the distributive property for real numbers.

Problem Find the product.

a. 2(x + 5)

b. x(3x − 2)

c. −8a³b⁵(2a² −7ab² −3)

d. x²(2x⁴ + 4x³ −3x + 6)

Solution

a. 2(x + 5)

Step 1.   Multiply each term of the polynomial by the monomial.

2(x + 5)

= 2 ⋅ x + 2 ⋅ 5

= 2x + 10

b. x(3x − 2)

Step 1.   Multiply each term of the polynomial by the monomial.

x(3x − 2)

= x ⋅ 3x − x ⋅ 2

= 3x² − 2x

c. −8a³b⁵(2a² −7ab² −3)

Be careful! Watch your exponents when you are multiplying polynomials by monomials.

Step 1.   Multiply each term of the polynomial by the monomial.

−8a³b⁵(2a²−7ab²−3)

= (−8a³b⁵)(2a²)−(−8a³b⁵)(7ab²)−(−8a³b⁵)(3)

= −16a⁵b⁵ + 56a⁴b⁷ + 24a³b⁵

d. x²(2x⁴ + 4x³ −3x + 6)

Step 1.   Multiply each term of the polynomial by the monomial.

x²(2x⁴ + 4x³−3x + 6)

= x² · 2x⁴ + x² · 4x³−x² · 3x + x² · 6

= 2x⁶ + 4x⁵−3x³ + 6x²

Multiplying Binomials

Multiplying Two Binomials

To multiply two binomials, multiply all the terms of the second binomial by each term of the first binomial and then simplify.

Problem   Find the product.

a. (2x + 3)(x − 5)

b. (a + b)(c + d)

Solution

a. (2x + 3)(x − 5)

Step 1.   Multiply all the terms of the second binomial by each term of the first binomial.

(2x + 3)(x−5)

= 2x · x + 2x · −5 + 3 · x + 3 · −5 Note: Mentally do this step.

= 2x² −10x + 3x−15

(2x + 3)(x−5) ≠ 2x² − 15. Don’t forget about −10 + 3x!

Step 2.   Simplify.

= 2x² −7x−15

Step 3.   Review your main result.

(2x + 3)(x−5) = 2x² −7x−15

b. (a + b)(c + d)

Step 1.   Multiply all the terms of the second binomial by each term of the first binomial.

(a + b)(c + d)

= a · c + a · d + b · c + b · d Note: Mentally do this step.

= ac + ad + bc + bd

Step 2.   Simplify.

There are no like terms, so ac + ad + bc + bd is simplified.

Step 3.   Review your main result.

(a + b)(c + d) = ac + ad + bc + bd

The FOIL Method

From the last problem, you can see that to find the product of two binomials, you compute four products, called partial products, using the terms of the two binomials. The FOIL method is a quick way to get those four partial products. Here is how FOIL works for finding the four partial products for (a + b)(c + d).

Be aware that the FOIL method works only for the product of two binomials.

Forgetting to compute the middle terms is the most common error when finding the product of two binomials.

1. Multiply the two First terms: a ⋅ c.

2. Multiply the two Outer terms: a ⋅ d.

3. Multiply the two Inner terms: b ⋅ c.

4. Multiply the two Last terms: b ⋅ d.

Notice that FOIL is an acronym for first, outer, inner, and last. The inner and outer partial products are the middle terms.

Here is an example.

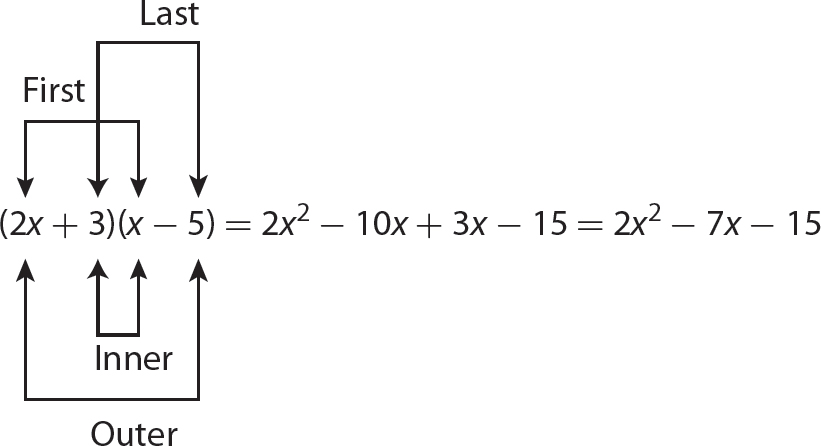
Problem   Find the product using the FOIL method.

a. (5x + 4)(2x − 3)

b. (x − 2)(x − 5)

c. (x − 2)(x + 5)

d. (x + y)²

Solution

a. (5x + 4)(2x − 3)

Step 1.   Find the partial products using the acronym FOIL.

(5x + 4)(2x−3)

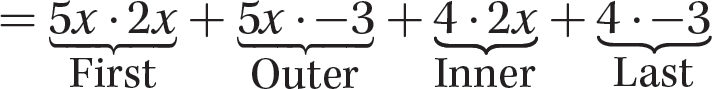Note: Mentally do this step.

= 10x² − 15x + 8x − 12

Step 2.   Simplify.

= 10x² − 7x − 12

Step 3.   Review your main result.

(5x + 4)(2x−3) = 10x² −7x−12

b. (x − 2)(x − 5)

Step 1.   Find the partial products using the acronym FOIL.

(x−2)(x−5)

x² − 5x − 2x + 10

Step 2.   Simplify.

= x²−7x + 10

Step 3.   Review your main result.

(x−2)(x + 5) = x²−7x + 10

c. (x−2)(x + 5)

Step 1.   Find the partial products using the acronym FOIL.

(x−2)(x + 5)

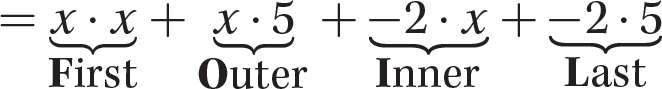
= x² + 5x −2x − 10

Step 2.   Simplify.

= x² + 3x−10

Step 3.   Review your main result.

(x−2)(x + 5) = x² + 3x−10

d. (x + y)²

Step 1.   Write as a product.

(x + y)² = (x + y)(x + y)

Put variable factors in alphabetical order.

Step 2.   Find the partial products using the acronym FOIL.

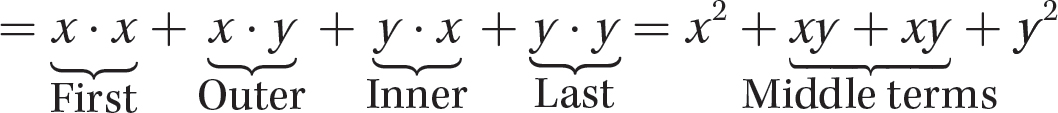
Step 3.   Simplify.

= x² + 2xy + y²

(x + y)² ≠ x² + y²! Don’t forget the middle terms!

Step 4.   Review the main steps.

(x + y)² = (x + y)(x + y) = x² + 2xy + y²

Multiplying Polynomials

Multiplying Two Polynomials

To multiply two polynomials, multiply all the terms of the second polynomial by each term of the first polynomial and then simplify.

Problem   Find the product.

a. (2x−1)(3x²−5x + 4)

b. (4x² + 2x−5)(2x²−x−3)

c. (x−2)(x² + 2x + 4)

As your skills improve, practice mentally reviewing the main steps.

Solution

a. (2x−1)(3x²−5x + 4)

Step 1.   Multiply all the terms of the second polynomial by each term of the first polynomial.

(2x−1)(3x²−5x + 4)

= 2x · 3x² + 2x · −5x + 2x · 4 + −1 · 3x² + −1 · −5x + −5x + 1 · 4      Note: Mentally do this step.

= 6x³ −10x² + 8x−3x² + 5x−4

Step 2.   Simplify.

= 6x³ −13x² + 13x−4

b. (4x² + 2x−5)(2x²−x−3)

Step 1.   Multiply all the terms of the second polynomial by each term of the first polynomial.

(4x² + 2x−5)(2x²−x−3)

= 4x² · 2x² + 4x² · −x + 4x² · −3 + 2x · 2x² + 2x · −x + 2x · −3 + −5 · 2x² + −5 · −x + −5 · −3

= 8x⁴ −4x³ −12x² + 4x³ −2x² −6x−10x² + 5x + 15

Step 2.   Simplify.

= 8x⁴ −24x² −x + 15

c. (x−2)(x² + 2x + 4)

Step 1.   Multiply all the terms of the second polynomial by each term of the first polynomial.

(x−2)(x² + 2x + 4)

= x · x² + x · 2x + x · 4 + −2 · x² + −2 · 2x + −2 · 4

= x³ + 2x² + 4x−2x² −4x−8

Step 2.   Simplify.

= x³ − 8

Special Products

The answer to part c of the last problem is an example of the “difference of two cubes.” It is a special product. Here is a list of special products that you need to know for algebra.

Memorizing special products is a winning strategy in algebra.

Special Products

Perfect Squares

(x + y)² = x² + 2xy + y²

(x−y)² = x²−2xy + y²

Difference of Two Squares

(x + y)(x−y) = x²−y²

Perfect Cubes

(x + y)³ = x³ + 3x²y + 3xy² + y³

(x−y)³ = x³−3x²y + 3xy²−y³

Sum of Two Cubes

(x + y)(x²−xy + y²) = x³ + y³

Difference of Two Cubes

(x−y)(x² + xy + y²) = x³−y³

Exercise 9

Find the product.

1. (4x⁵y³)(−3x²y³)

2. (−8a⁴b³)(5ab²)

3. (−10x³)(−2x²)

4. (−3x²y⁵)(6xy⁴)(−2xy)

5. 3(x − 5)

6. x(3x² − 4)

7. −2a²b³(3a² − 5ab² − 10)

8. (2x − 3)(x + 4)

9. (x + 4)(x + 5)

10. (x − 4)(x − 5)

11. (x + 4)(x − 5)

12. (x − 4)(x + 5)

13. (x − 1)(2x² − 5x + 3)

14. (2x² + x − 3)(5x² − x − 2)

15. (x − y)²

16. (x + y)(x − y)

17. (x + y)³

18. (x − y)³

19. (x + y)(x² − xy + y²)

20. (x − y)(x² + xy + y²)