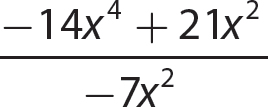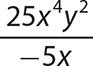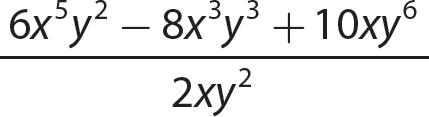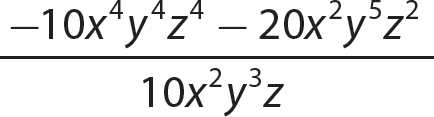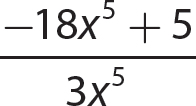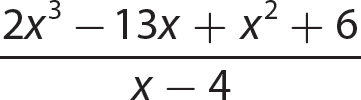This chapter presents a discussion of division of polynomials. Division of polynomials is analogous to division of real numbers. In algebra, you indicate division using the fraction bar. For example, 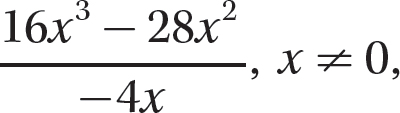 indicates 16x3 − 28x2 divided by −4x. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the divisor 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
indicates 16x3 − 28x2 divided by −4x. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the divisor 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
Dividing a Polynomial by a Monomial
Customarily, a division problem is a dividend divided by a divisor. When you do the division, you get a quotient and a remainder. You express the relationship between these quantities as


Dividing a Polynomial by a Monomial
To divide a polynomial by a monomial, divide each term of the polynomial by the monomial.
To avoid sign errors when you are doing division of polynomials, keep a − symbol with the number that follows it. You likely will need to properly insert a + symbol when you do this.
You will see this tactic illustrated in the following problem.
Problem Find the quotient and remainder.
a. 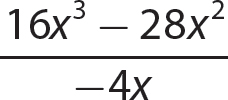
b. 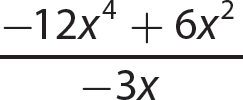
c. 
d. 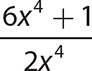
e. 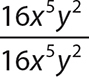
Solution
a. 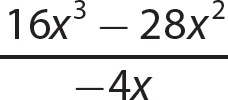

Step 1. Divide each term of the polynomial by the monomial.
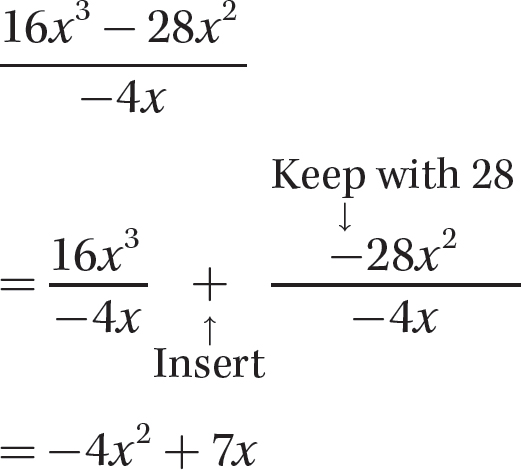
Step 2. State the quotient and remainder.
The quotient is −4x2 + 7x and the remainder is 0.
b. 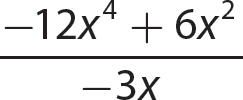

Step 1. Divide each term of the polynomial by the monomial.
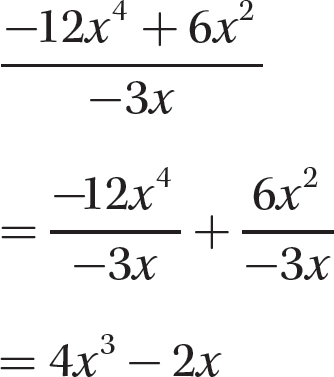
Step 2. State the quotient and remainder.
The quotient is 4x3 −2x and the remainder is 0.
c. 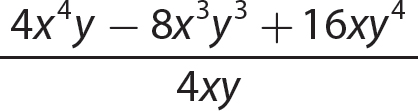

Step 1. Divide each term of the polynomial by the monomial.
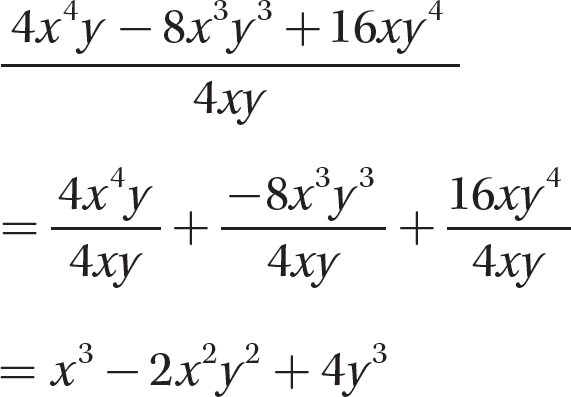
Step 2. State the quotient and remainder.
The quotient is x3−2x2y2 + 4y3 and the remainder is 0.
d. 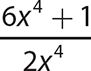

Step 1. Divide each term of the polynomial by the monomial.
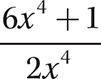
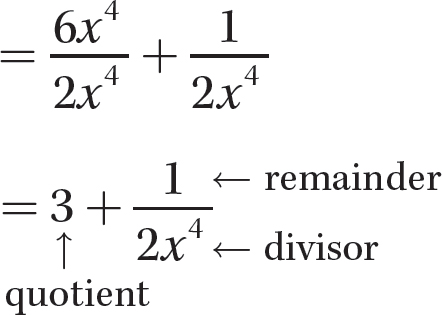
Step 2. State the quotient and remainder.
The quotient is 3 and the remainder is 1.
e. 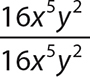

Step 1. Divide 16x5y2 by 16x5y2.
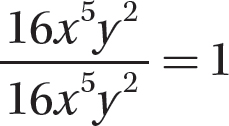
Step 2. State the quotient and remainder.
The quotient is 1 and the remainder is 0.
Dividing a Polynomial by a Polynomial
When you divide two polynomials, and the divisor is not a monomial, you use long division. The procedure is very similar to the long division algorithm of arithmetic. The steps are illustrated in the following problem.
Problem Find the quotient and remainder.
a. 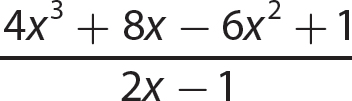
b. 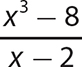
c. 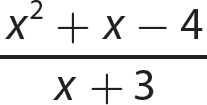
Solution
a. 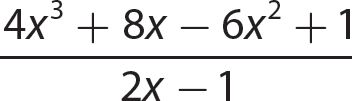

Step 1. Using the long division symbol  arrange the terms of both the dividend and the divisor in descending powers of the variable x.
arrange the terms of both the dividend and the divisor in descending powers of the variable x.

Step 2. Divide the first term of the dividend by the first term of the divisor and write the answer as the first term of the quotient.
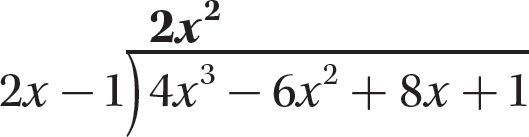
Step 3. Multiply 2x − 1 by 2x2 and enter the product under the dividend.
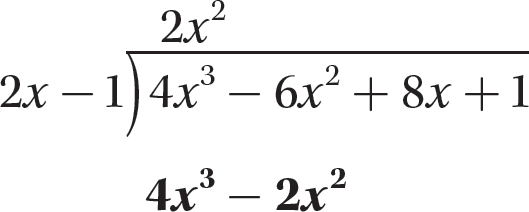
Step 4. Subtract 4x3 −2x2 from the dividend, being sure to mentally change the signs of both 4x3 and −2x2.
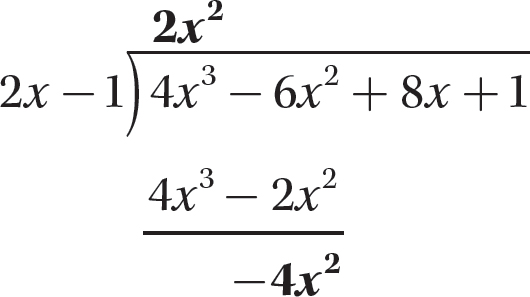
Step 5. Bring down +8x, the third term of the dividend, and repeat steps 2–4.
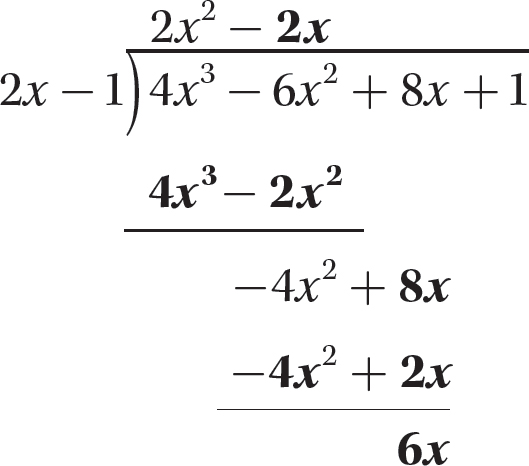
Step 6. Bring down +1, the last term of the dividend, and repeat steps 2–4.
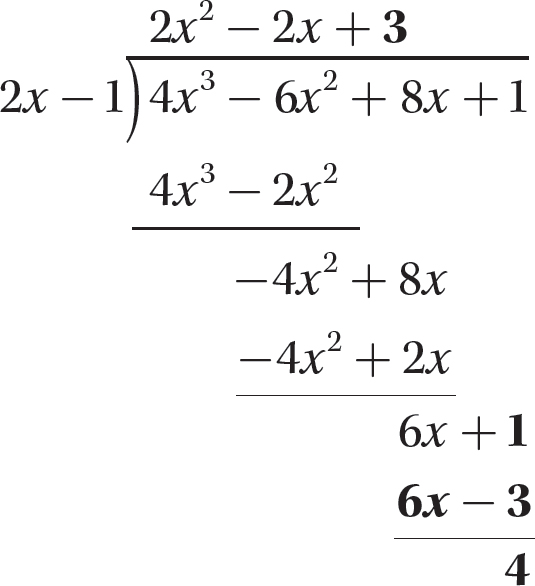
Step 7. State the quotient and remainder.
The quotient is 2x2 −2x + 3 and the remainder is 4.
b. 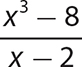

Step 1. Using the long division symbol 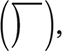 arrange the terms of both the dividend and the divisor in descending powers of the variable x. Insert zeros as placeholders for missing powers of x.
arrange the terms of both the dividend and the divisor in descending powers of the variable x. Insert zeros as placeholders for missing powers of x.
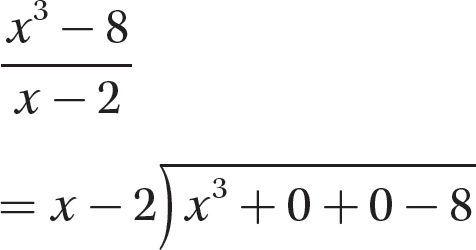
Step 2. Divide the first term of the dividend by the first term of the divisor and write the answer as the first term of the quotient.
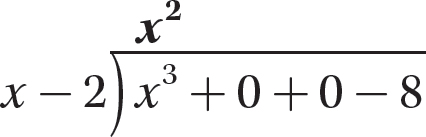
Step 3. Multiply x − 2 by x2 and enter the product under the dividend.
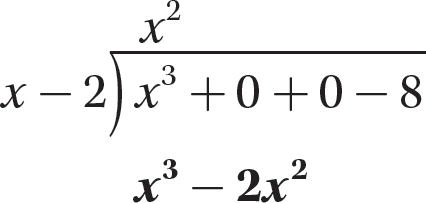
Step 4. Subtract x3−2x2 from the dividend, being sure to mentally change the signs of both x3 and −2x2.
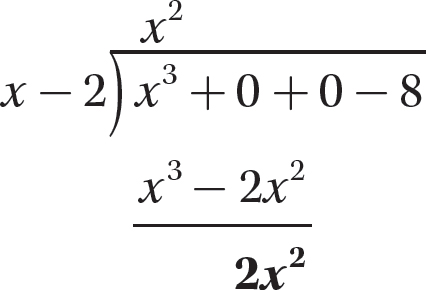
Step 5. Bring down +0, the third term of the dividend, and repeat steps 2–4.
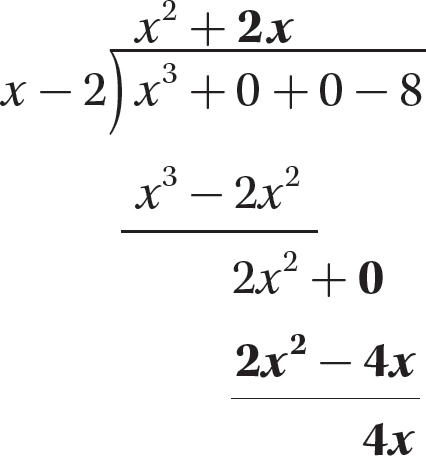
Step 6. Bring down −8, the last term of the dividend, and repeat steps 2–4.
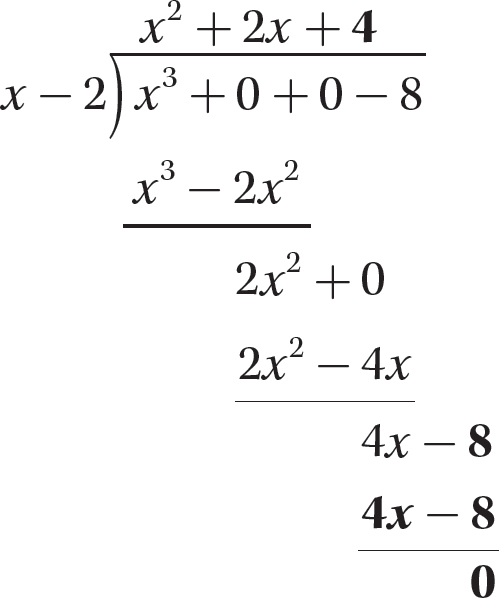
Step 7. State the quotient and remainder.
The quotient is x2 + 2x + 4 and the remainder is 0.
c. 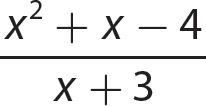

Step 1. Using the long division symbol 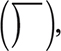 arrange the terms of both the dividend and the divisor in descending powers of the variable x.
arrange the terms of both the dividend and the divisor in descending powers of the variable x.
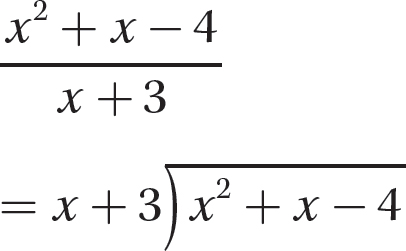
Step 2. Divide the first term of the dividend by the first term of the divisor and write the answer as the first term of the quotient.
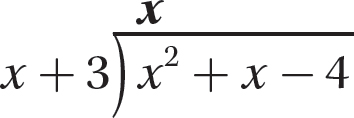
Step 3. Multiply x + 3 by x and enter the product under the dividend.
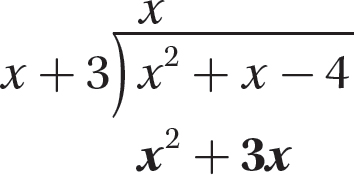
Step 4. Subtract x2 + 3x from the dividend, being sure to mentally change the signs of both x2 and 3x.
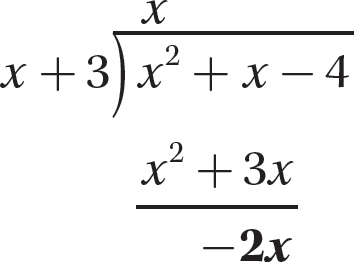
Step 5. Bring down −4, the third term of the dividend, and repeat steps 2–4.
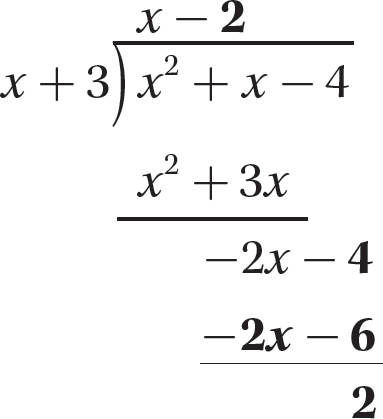
Step 6. State the quotient and remainder.
The quotient is x − 2 and the remainder is 2.
Exercise 11

Find the quotient and remainder.

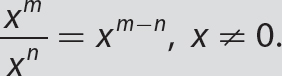 = xm − n, x ≠ 0.
= xm − n, x ≠ 0.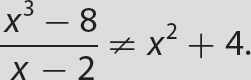 Avoid this common error.
Avoid this common error.