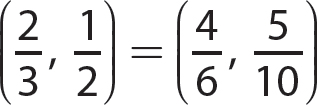In this chapter, you learn about the Cartesian coordinate plane.
Definitions for the Plane
The Cartesian coordinate plane is defined by two real number lines, one horizontal and one vertical, intersecting at right angles at their zero points (see Figure 16.1). The two real number lines are the coordinate axes. The horizontal axis, commonly called the x-axis, has positive direction to the right, and the vertical axis, commonly referred to as the y-axis, has positive direction upward. The two axes determine a plane. Their point of intersection is called the origin.
Figure 16.1 Cartesian coordinate plane
Ordered Pairs in the Plane
In the (Cartesian) coordinate plane, you identify each point P in the plane by an ordered pair (x, y) of real numbers x and y, called its coordinates. The ordered pair (0, 0) names the origin. An ordered pair of numbers is written in a definite order so that one number is first and the other second. The first number is the x-coordinate, and the second number is the y-coordinate (see Figure 16.2). The order in the ordered pair (x, y) that corresponds to a point P is important. The absolute value of the first coordinate, x, is the perpendicular horizontal distance (right or left) of the point P from the y-axis. If x is positive, P is to the right of the y-axis; if x is negative, it is to the left of the y-axis. The absolute value of the second coordinate, y, is the perpendicular vertical distance (up or down) of the point P from the x-axis. If y is positive, P is above the x-axis; if y is negative, it is below the x-axis.
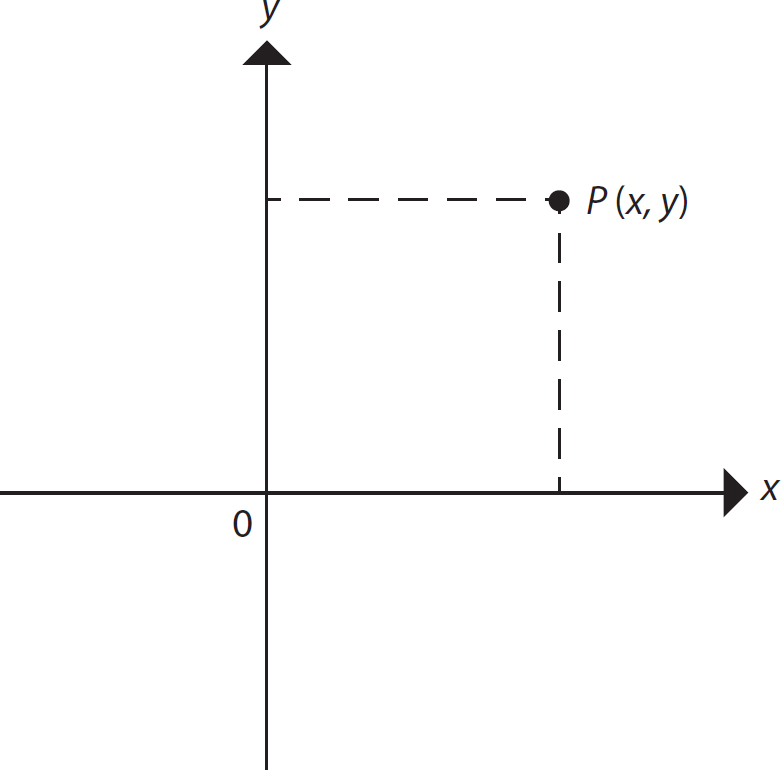
Figure 16.2 Point P in a Cartesian coordinate plane
Problem Name the ordered pair of integers corresponding to point A in the coordinate plane shown.
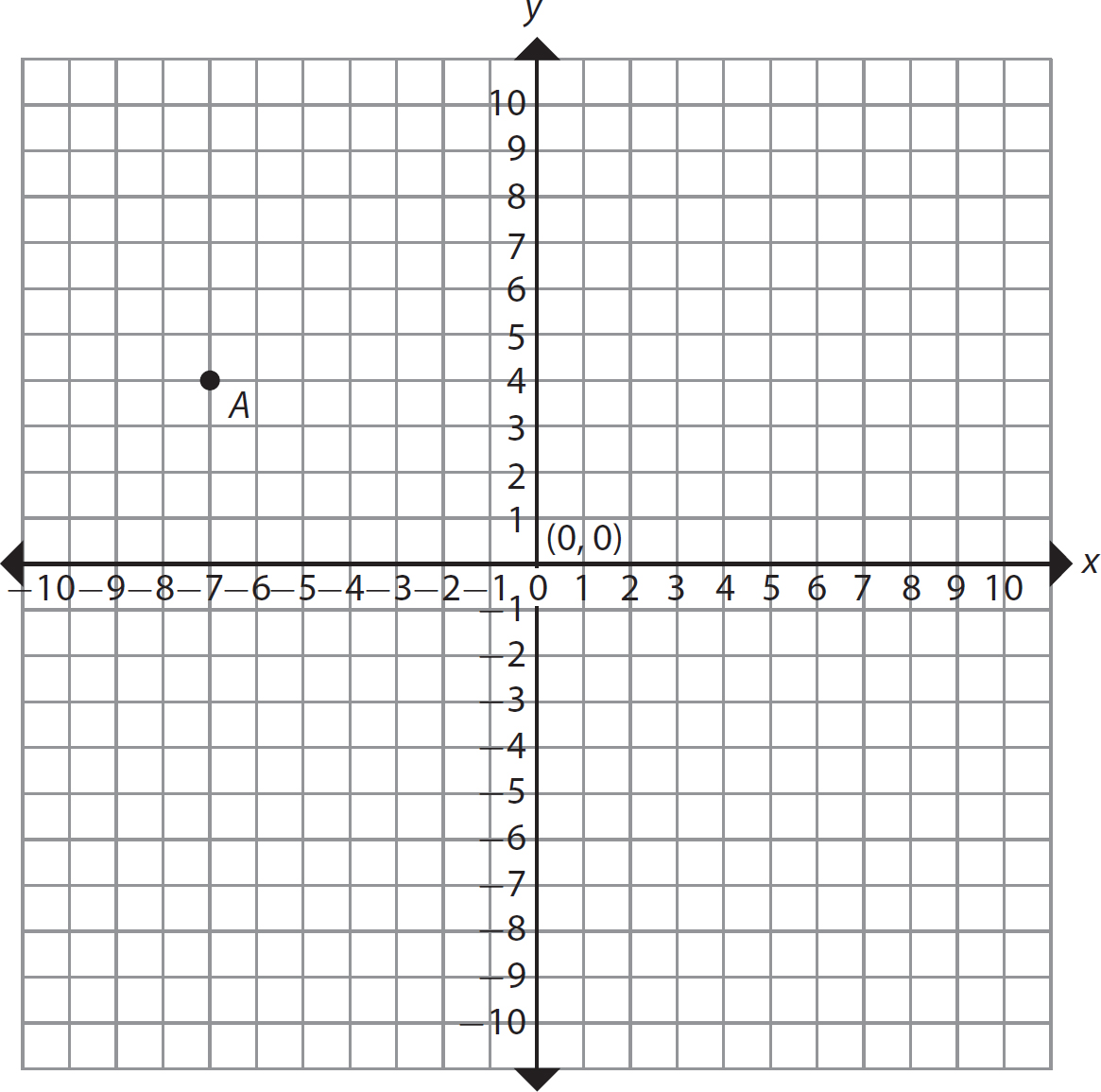
Solution

Step 1. Determine the x-coordinate of A.
The point A is 7 units to the left of the y-axis, so it has x-coordinate −7.
Step 2. Determine the y-coordinate of A.
The point A is 4 units above the x-axis, so it has y-coordinate 4.
Step 3. Name the ordered pair corresponding to point A.
(−7, 4) is the ordered pair corresponding to point A.
Two ordered pairs are equal if and only if their corresponding coordinates are equal; that is, (a, b) = (c, d) if and only if a = c and b = d.
Problem State whether the two ordered pairs are equal. Explain your answer.
a. (2, 7), (7, 2)
b. (−3, 5), (3, 5)
c. (−4, −1), (4, 1)
d. 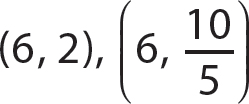
Solution
a. (2, 7), (7, 2)

Step 1. Check whether the corresponding coordinates are equal.
(2, 7) ≠ (7, 2) because 2 and 7 are not equal.
b. (−3, 5), (3, 5)

Step 1. Check whether the corresponding coordinates are equal.
(−3, 5) ≠ (3, 5) because −3 ≠ 3.
c. (−4, −1), (4, 1)

Step 1. (−4, −1) ≠ (4, 1) either because −4 ≠ 4 or because −1 ≠ 1.
d. 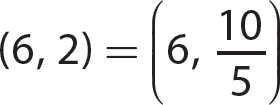 because 6 = 6 and
because 6 = 6 and 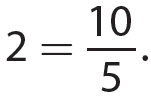
Quadrants of the Plane
The axes divide the Cartesian coordinate plane into four quadrants. The quadrants are numbered with Roman numerals—I, II, III, and IV—beginning in the upper right and going around counterclockwise, as shown in Figure 16.3.
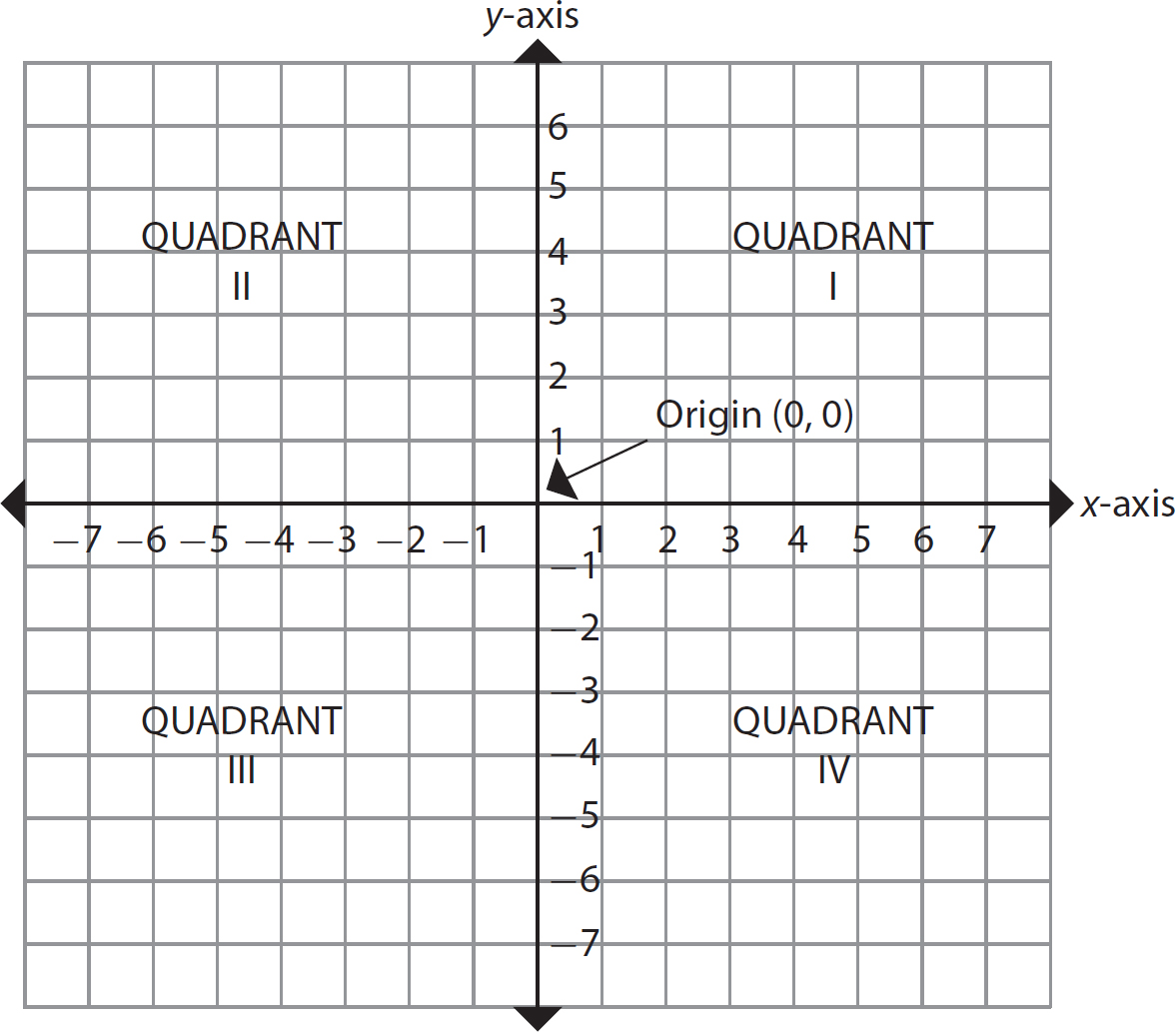
Figure 16.3 Quadrants in the coordinate plane
In quadrant I, both coordinates are positive; in quadrant II, the x-coordinate is negative, and the y-coordinate is positive; in quadrant III, both coordinates are negative; and in quadrant IV, the x-coordinate is positive and the y-coordinate is negative. Points that have 0 as one or both of the coordinates are on the axes. If the x-coordinate is 0, the point lies on the y-axis. If the y-coordinate is 0, the point lies on the x-axis. If both coordinates of a point are 0, the point is at the origin.
Problem Identify the quadrant in which the point lies.
a. (4, −8)
b. (1, 6)
c. (−8, −3)
d. (−4, 2)
Solution
a. (4, −8)

Step 1. Note the signs of x and y.
x is positive and y is negative.
Step 2. Identify the quadrant in which the point lies.
Because x is positive and y is negative, (4, −8) lies in quadrant IV.
b. (1, 6)

Step 1. Note the signs of x and y.
x is positive and y is positive.
Step 2. Identify the quadrant in which the point lies.
Because x is positive and y is positive, (1, 6) lies in quadrant I.
c. (−8, −3)

Step 1. Note the signs of x and y.
x is negative and y is negative.
Step 2. Identify the quadrant in which the point lies.
Because x is negative and y is negative, (−8, −3) lies in quadrant III.
d. (−4, 2)

Step 1. Note the signs of x and y.
x is negative and y is positive.
Step 2. Identify the quadrant in which the point lies.
Because x is negative and y is positive, (−4, 2) lies in quadrant II.
Finding the Distance Between Two Points in the Plane
If you have two points in a coordinate plane, you can find the distance between them using the formula given here.

Distance Between Two Points
The distance d between two points (x1, y1) and (x2, y2) in a coordinate plane is given by
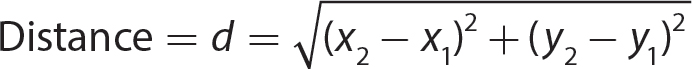
Problem Find the distance between the points (−1, 4) and (5, −3).
Solution

Step 1. Specify (x1, y1) and (x2, y2) and identify values for x1, y1, x2, and y2.
Let (x1, y1) = (-1, 4) and (x2, y2) = (5, −3). Then x1 = −1, y1 = 4, x2 = 5, and y2 = −3.
Step 2. Evaluate the formula for the values from step 1.
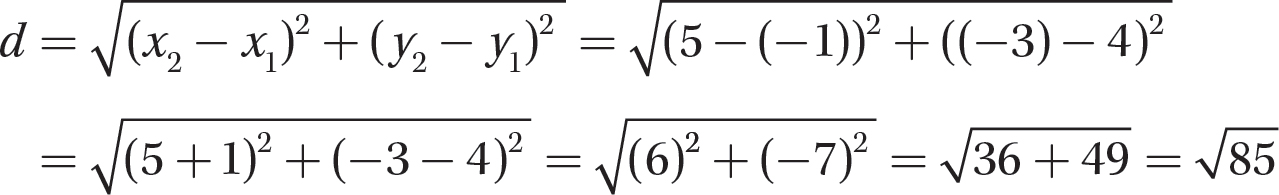
Step 3. State the distance.
The distance between (−1, 4) and (5, −3) is 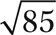 units.
units.
Finding the Midpoint Between Two Points in the Plane
You can find the midpoint between two points using the following formula.

Midpoint Between Two Points
The midpoint between two points (x1,y1) and (x2,y2) in a coordinate plane is the point with coordinates
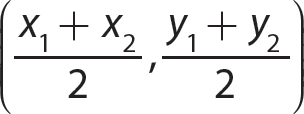
Problem Find the midpoint between (−1, 4) and (5, −3).
Solution

Step 1. Specify (x1,y1) and (x2,y2) and identify values for x1, y1, x2, and y2.
Let (x1,y1) = (-1, 4) and (x2,y2) = (-5, 3). Then x1 = -1, y1 = 4, x2 = 5, and y2 = -3.
Step 2. Evaluate the formula for the values from step 1.
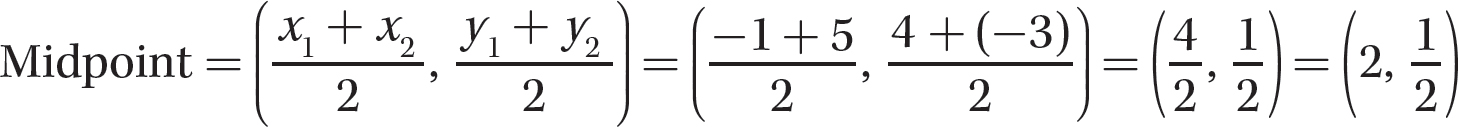
Step 3. State the midpoint.
The midpoint between (−1, 4) and (5, −3) is 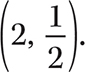
Finding the Slope of a Line Through Two Points in the Plane
When you have two distinct points in a coordinate plane, you can construct the line through the two points. The slope describes the steepness or slant (if any) of the line. To calculate the slope of a line, use the following formula.

Slope of a Line Through Two Points
The slope m of a line through two distinct points, (x1, y1) and (x2, y2), is given by
Slope = 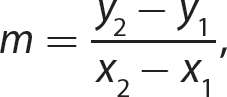 , provided x1 ≠ x2
, provided x1 ≠ x2
From the formula, you can see that the slope is the ratio of the change in vertical coordinates (the rise) to the change in horizontal coordinates (the run). Thus, 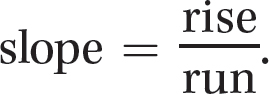 Figure 16.4 illustrates the rise and run for the slope of the line through points P1(x1, y1) and P2(x2, y2).
Figure 16.4 illustrates the rise and run for the slope of the line through points P1(x1, y1) and P2(x2, y2).
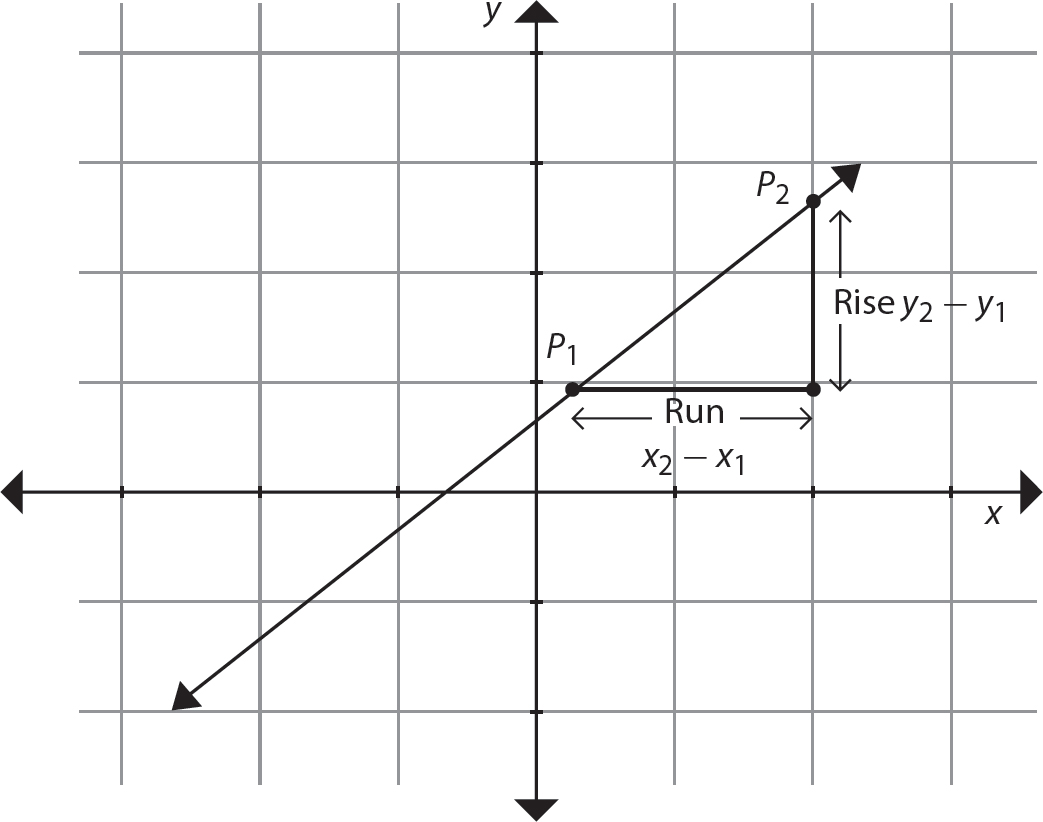
Figure 16.4 Rise and run
Lines that slant upward from left to right have positive slopes, and lines that slant downward from left to right have negative slopes. Also, horizontal lines have zero slope, but the slope for vertical lines is undefined.
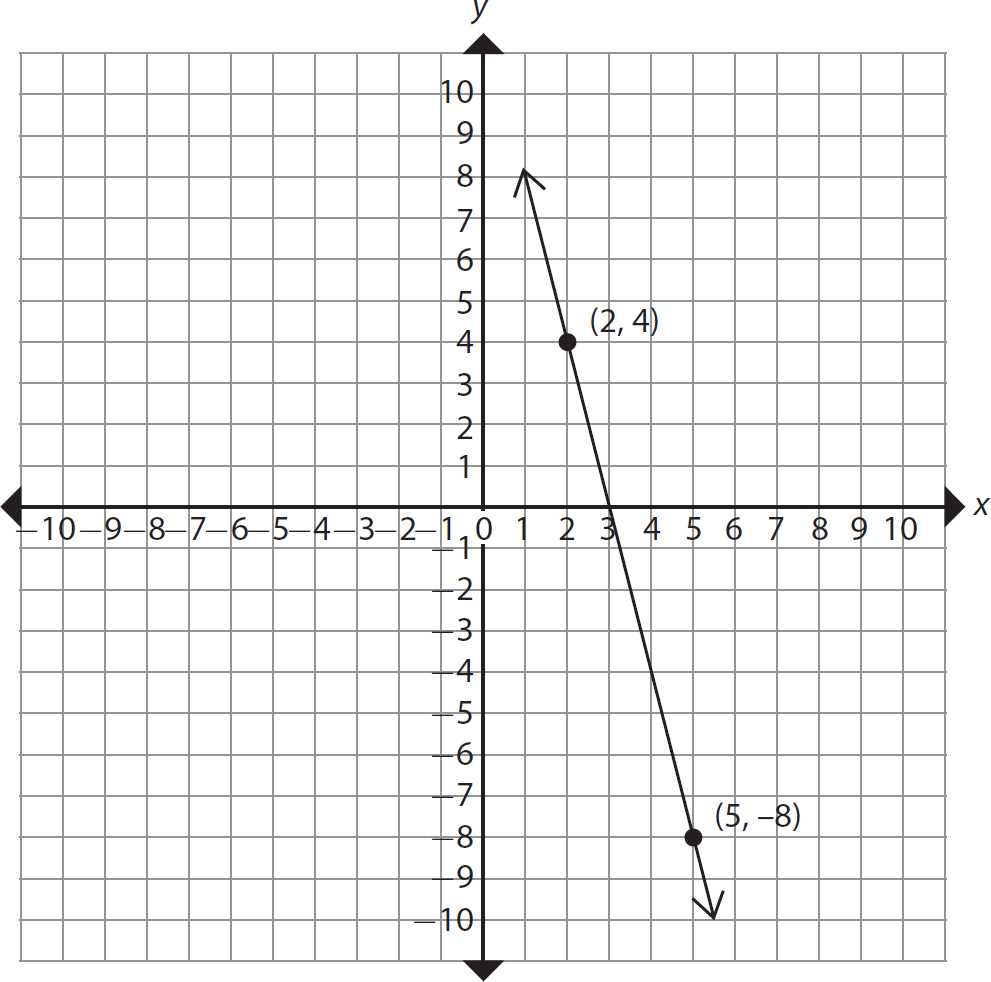
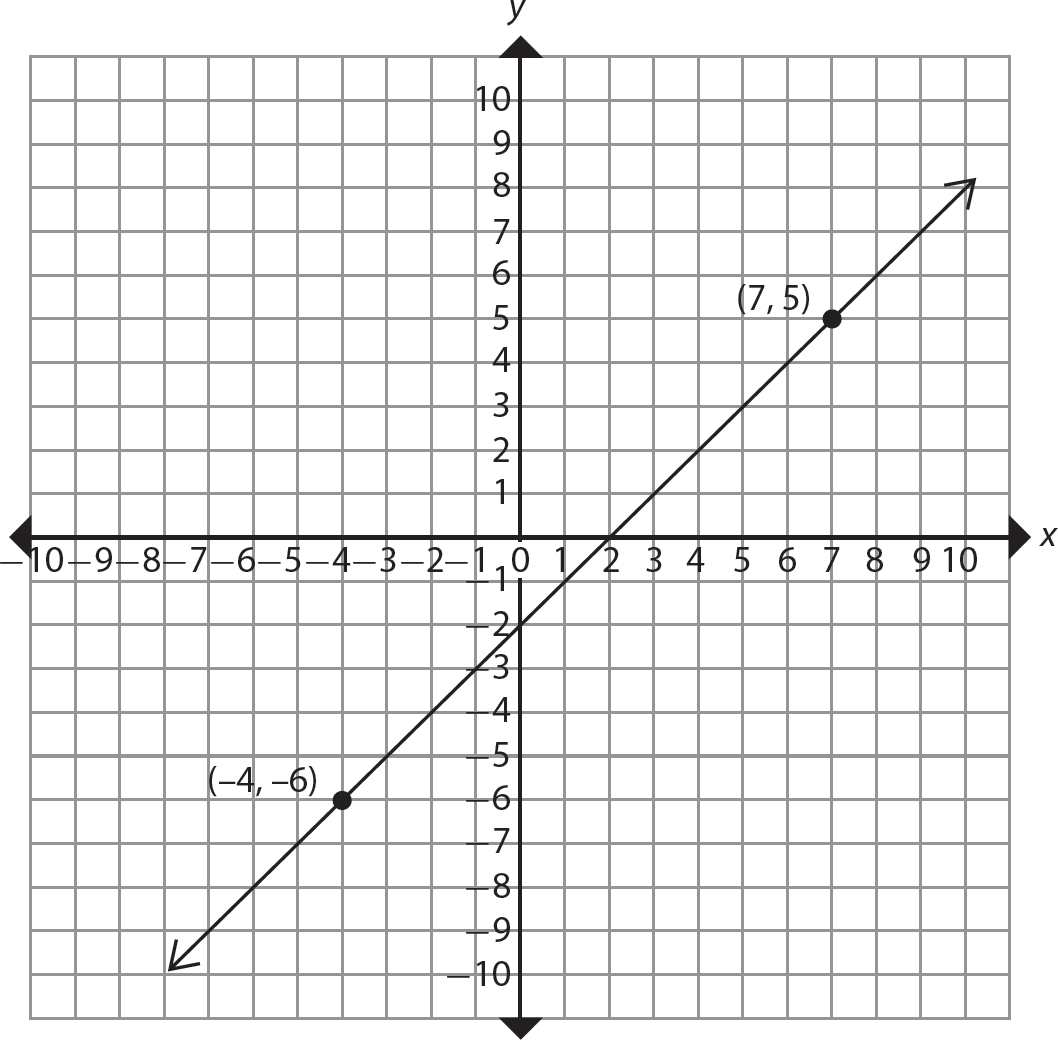
Problem Find the slope of the line through the points shown.
Solution

Step 1. Specify (x1, y1) and (x2, y2) and identify values for x1, y1, x2, and y2.
Let (x1, y1) = (7, 5) and (x2, y2) = (-4, -6). Then x1 = 7, y1 = 5, x2 = -4, and y2 = -6.
Step 2. Evaluate the formula for the values from step 1.
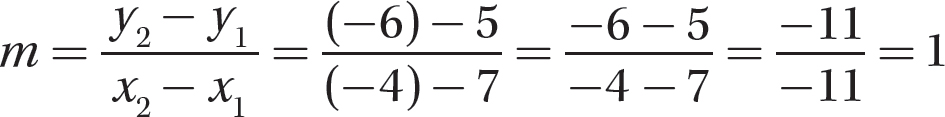
Step 3. State the slope.
The slope of the line that passes through the points (7, 5) and (−4, −6) is 1. Note: The line slants upward from left to right—so the slope should be positive.
Problem Find the slope of the line through the two points.
a. (−1, 4) and (5, −3)
b. (−6, 7) and (5, 7)
c. (5, 8) and (5, −3)
Solution
a. (−1, 4) and (5, −3)

Step 1. Specify (x1, y1) and (x2, y2) and identify values for x1, y1, x2, and y2.
Let (x1, y1) = (-1, 4) and (x2, y2) = (5, -3). Then x1 = -1, y1 = 4, x2 = 5, and y2 = -3.
Step 2. Evaluate the formula for the values from step 1.
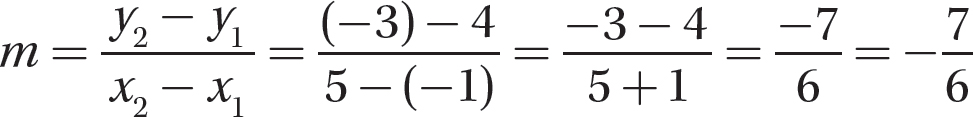
Step 3. State the slope.
The slope of the line through (−1, 4) and (5, −3) is 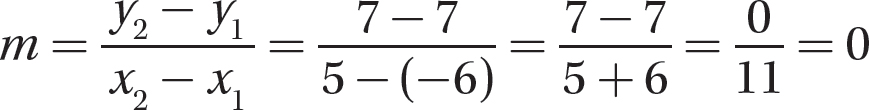 . Note: If you sketch the line through these two points, you will see that it slants downward from left to right—so its slope should be negative.
. Note: If you sketch the line through these two points, you will see that it slants downward from left to right—so its slope should be negative.
b. (−6, 7) and (5, 7)

Step 1. Specify (x1, y1) and (x2, y2) and identify values for x1, y1, x2, and y2.
Let (x1, y1) = (-6, 7) and (x2, y2) = (5, 7). Then x1 = -6, y1 = 7, x2 = 5, and y2 = 7.
Step 2. Evaluate the formula for the values from step 1.
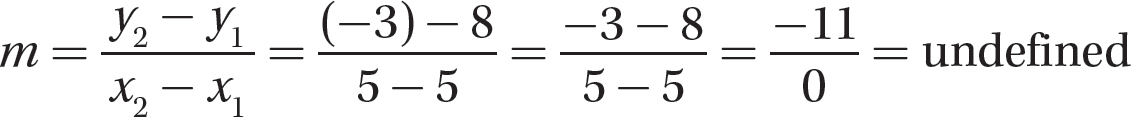
Step 3. State the slope.
The slope of the line that contains (−6, 7) and (5, 7) is 0. Note: If you sketch the line through these two points, you will see that it is a horizontal line—so the slope should be 0.
c. (5, 8) and (5, −3)

Step 1. Specify (x1, y1) and (x2, y2) and identify values for x1, y1, x2, and y2.
Let (x1, y1) = (-6, 7) and (x2, y2) = (5, 8). Then x1 = 5, y1 = 8, x2 = 5, and y2 = -3.
Step 2. Evaluate the formula for the values from step 1.
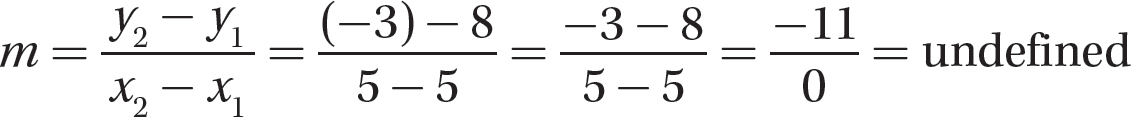
Step 3. State the slope.
The slope of the line that contains (5, 8) and (5, −3) is undefined. Note: If you sketch the line through these two points, you will see that it is a vertical line—so the slope should be undefined.
Slopes of Parallel and Perpendicular Lines
It is useful to know the following:

If two lines are parallel, their slopes are equal; if two lines are perpendicular, their slopes are negative reciprocals of each other.
Problem Find the indicated slope.
a. Find the slope m1 of a line that is parallel to the line through (−3, 4) and (−1, −2).
b. Find the slope m2 of a line that is perpendicular to the line through (−3, 4) and (−1, −2).
Solution
a. Find the slope m1 of a line that is parallel to the line through (−3, 4) and (−1, −2).

Step 1. Determine a strategy.
Because two parallel lines have equal slopes, m1 will equal the slope m of the line through (−3, 4) and (−1, −2); that is, m1 = m.
Step 2. Find m.
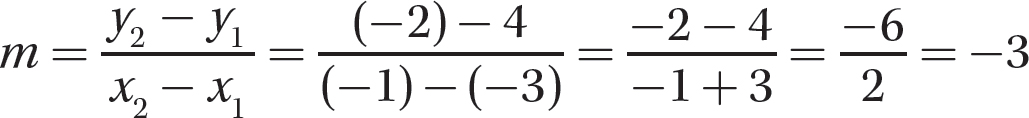
Step 3. Determine m1.
m1 = m = −3
b. Find the slope m2 of a line that is perpendicular to the line through (−3, 4) and (−1, −2).

Step 1. Determine a strategy.
Because the slopes of two perpendicular lines are negative reciprocals of each other, m2 will equal the negative reciprocal of the slope m of the line through (−3, 4) and (−1, −2); that is, 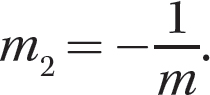 .
.
Step 2. Find m.
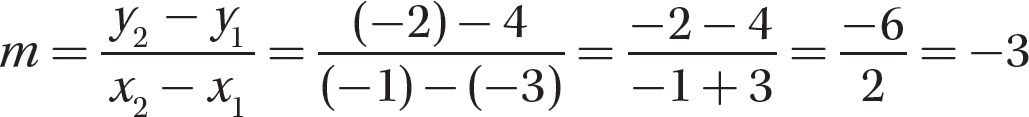
Step 3. Determine m2.
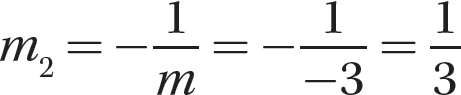

Exercise 16
For 1–6, indicate whether the statement is true or false.
1. The intersection of the coordinate axes is the origin.
2. (2, 3) = (3, 2)
4. The point 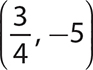 is in quadrant II.
is in quadrant II.
5. The point 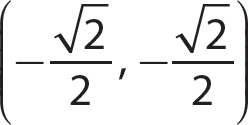 is in quadrant III.
is in quadrant III.
6. The point (5, 0) is in quadrant I.
For 7–14, fill in the blank to make a true statement.
7. The change in y-coordinates between two points on a line is the __________.
8. The change in x-coordinates between two points on a line is the __________.
9. Lines that slant downward from left to right have __________ slopes.
10. Lines that slant upward from left to right have __________ slopes.
11. Horizontal lines have __________ slope.
12. The slope of a line that is parallel to a line that has slope 2/3 is __________.
13. The slope of a line that is perpendicular to a line that has slope 3/4 is __________.
14. The slope of a vertical line is __________.
15. Name the ordered pair of integers corresponding to point K in the following coordinate plane.
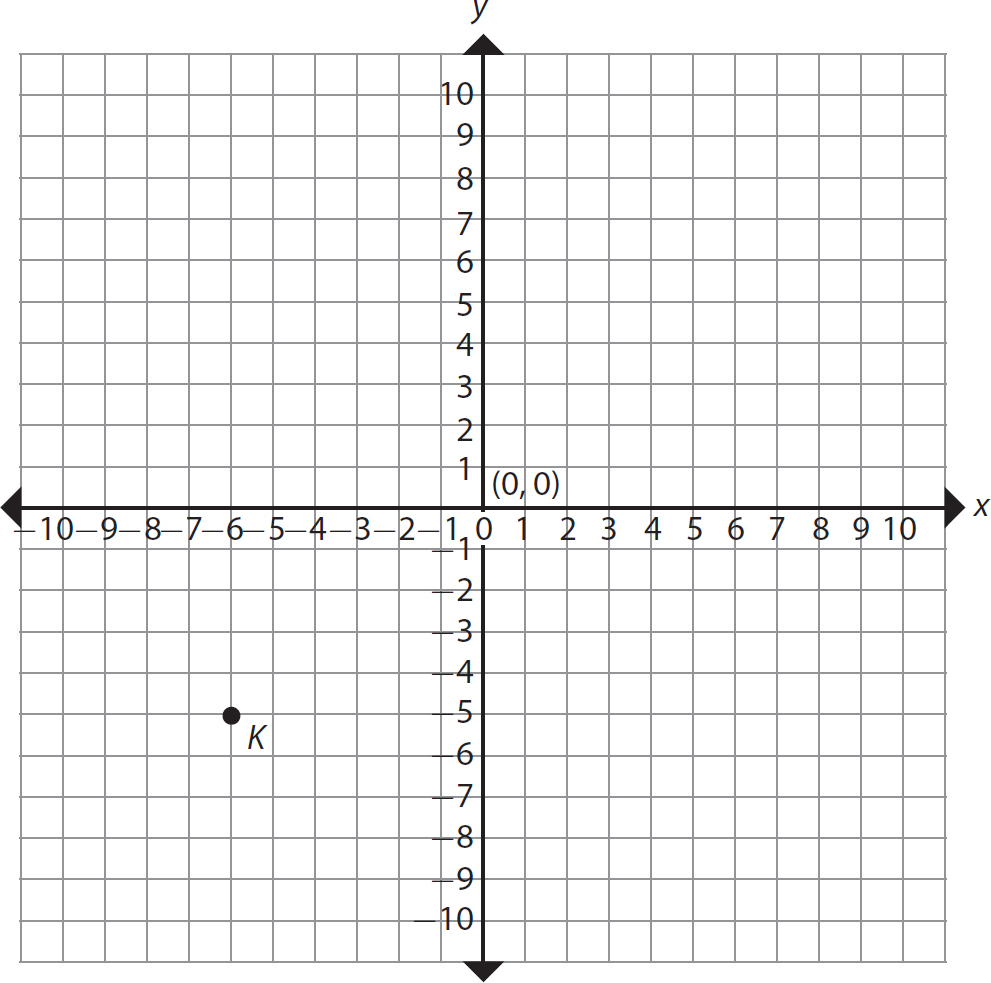
16. Find the distance between the points (1, 4) and (5, 7).
17. Find the distance between the points (−2, 5) and (4, −1).
18. Find the midpoint between the points (−2, 5) and (4, −1).
19. Find the slope of the line through (−2, 5) and (4, −1).
20. Find the slope of the line through the points shown.