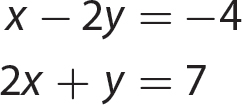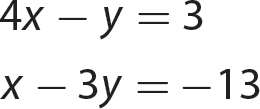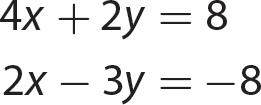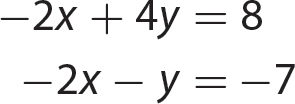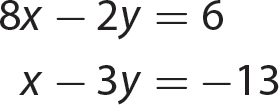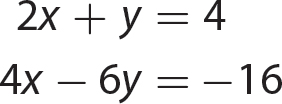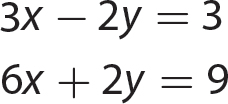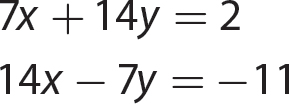20

Systems of Equations

In algebra, you might need to solve two linear equations in two variables and to solve them simultaneously. Three methods for solving two simultaneous equations are presented in this chapter.

Solutions to a System of Equations

From Chapter 19, the equation of a linear function has several forms, but for the purposes of this chapter, the form ax + by = c is preferred. You know from Chapter 17 that the graph of a linear equation is a line. When you encounter two such equations, the basic question you should ask yourself is, “What are the coordinates of the point of intersection, if any, of the two lines?”

Remember from Chapter 16 that the location of a point is an ordered pair of coordinates such as (x, y).

This question has three possible answers. If the lines do not intersect, there is no solution. If the two lines intersect, there is only one solution—an ordered pair (x, y). If the two lines are equal versions of the same line, then there are infinitely many solutions—an infinite set of ordered pairs.

Finally, when you are solving two linear equations in two variables, an example of the standard form of writing them together is

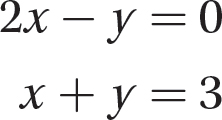
You solve the system when you answer the question: What are the coordinates of the point of intersection, if any, of the two lines? Here are three methods for solving a system of equations.

Solving a System of Equations by Substitution

To solve a system of equations by substitution, you solve one equation for one of the variables in terms of the other variable and then use substitution to solve the system. (See Chapter 14 for a discussion on how to solve linear equations.)

Problem   Solve the system.

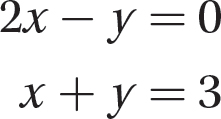
Solution

Step 1.   Solve the first equation, 2x − y = 0, for y in terms of x.

When you use the substitution method, enclose substituted values in parentheses to avoid errors.

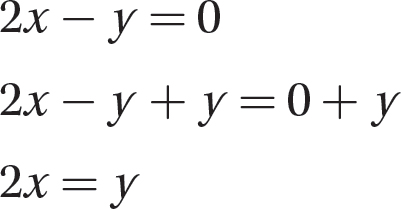
Step 2.   Substitute 2x for y in the second equation, x + y = 3, and solve for x.

x + (2x) = 3

3x = 3

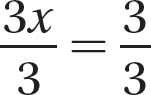
x = 1

When you use the substitution method, you can substitute the value for x in either equation. Just pick the one you think would be easier to work with.

Step 3.   Substitute 1 for x in the second equation, x + y = 3, and solve for y.

1 + y = 3

1 + y − 1 = 3 − 1

y = 2

Always check your solution in both equations when you solve a system of two linear equations.

Step 4.   Check whether x = 1 and y = 2 satisfy both equations in the system.

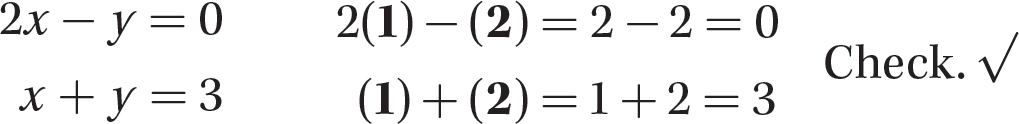
Step 5.   Write the solution.

The solution is x = 1 and y = 2. That is, the two lines intersect at the point (1, 2).

When you use the substitution method, it makes no difference which equation is solved first or for which variable, but when you solve it, be sure to substitute the value in the other equation.

Problem   Solve the system.

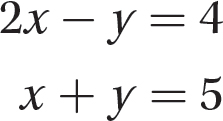
Solution

Step 1.   Solve the second equation, x + y = 5, for x in terms of y.

Step 2.   Substitute 5 − y for x in the first equation, 2x − y = 4, and solve for y.

Step 3.   Substitute 2 for y in the second equation, x + y = 5, and solve for x.

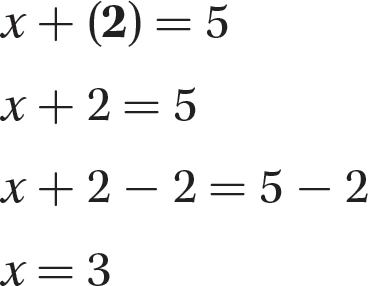
Step 4.   Check whether x = 3 and y = 2 satisfy both equations.

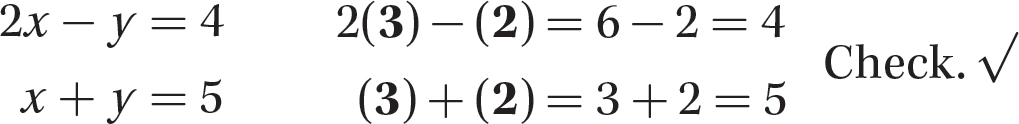
Step 5.   Write the solution.

The solution is x = 3 and y = 2. That is, the two lines intersect at the point (3, 2).

Solving a System of Equations by Elimination

To solve a system of equations by elimination, you multiply the equations by constants to produce opposite coefficients of one variable so that it can be eliminated by adding the two equations.

Problem   Solve the system.

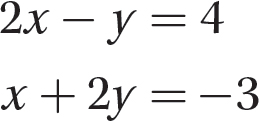
Solution

Step 1.   To eliminate x, multiply the second equation by −2.

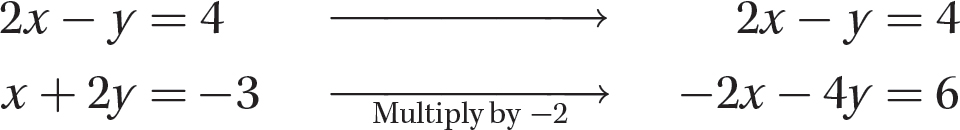
Step 2.   Add the resulting two equations.

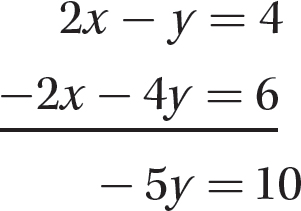
Step 3.   Solve −5y = 10 for y.

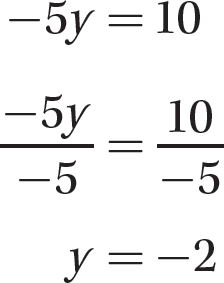
Step 4.   Substitute −2 for y in one of the original equations, 2x−y = 4, and solve for x.

2x − (−2) = 4

Step 5.   Check whether x = 1 and y = − 2 satisfy both original equations.

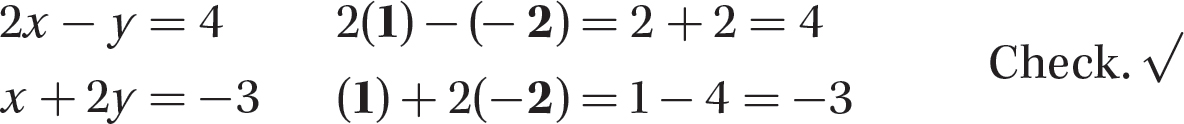
Step 6.   Write the solution.

The solution is x = 1 and y = − 2. That is, the two lines intersect at the point (1, −2).

Problem   Solve the system.

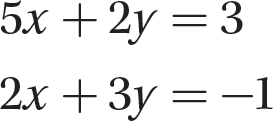
Solution

Step 1.   To eliminate y, multiply the first equation by 3 and the second equation by −2.

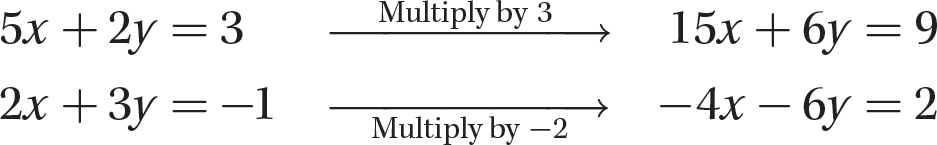
Step 2.   Add the resulting two equations.

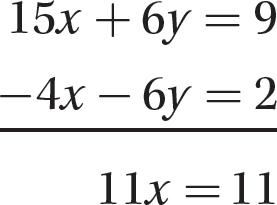
Step 3.   Solve 11x = 11 for x.

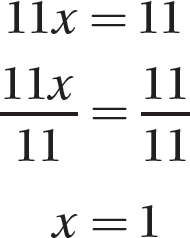
Step 4.   Substitute 1 for x in one of the original equations, 5x + 2y = 3, and solve for y.

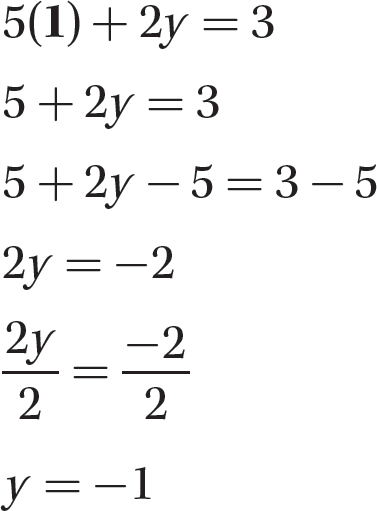
Step 5.   Check whether x = 1 and y = − 1 satisfy both original equations.

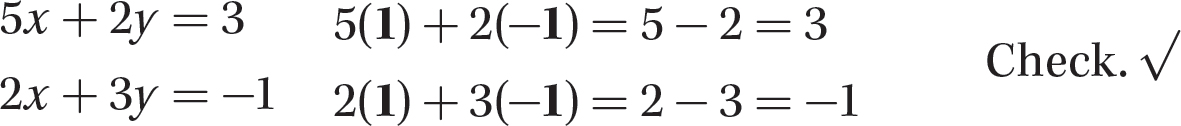
Step 6.   Write the solution.

The solution is x = 1 and y = − 1. That is, the two lines intersect at the point (1, −1).

Solving a System of Equations by Graphing

The graphing method might yield inaccurate results due to the limitations of graphing.

To solve a system of equations by graphing, you graph the two equations and locate (as accurately as possible) the intersection point on the graph. Because graphing devices such as graphing calculators and computer algebra systems require the slope-intercept form of the equation of straight lines, the steps will include writing the equations in that form. (See Chapter 17 for a discussion of the slope-intercept form.)

Problem   Solve the system.

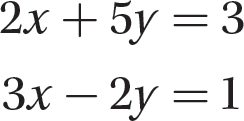
Solution

Step 1.   Write both equations in slope-intercept form.

The first equation, 2x + 5y = 3, yields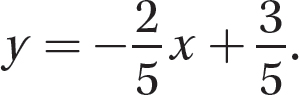

The second equation, 3x−2y = 1, yields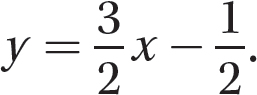

Step 2.   Graph both equations on the same coordinate plane.

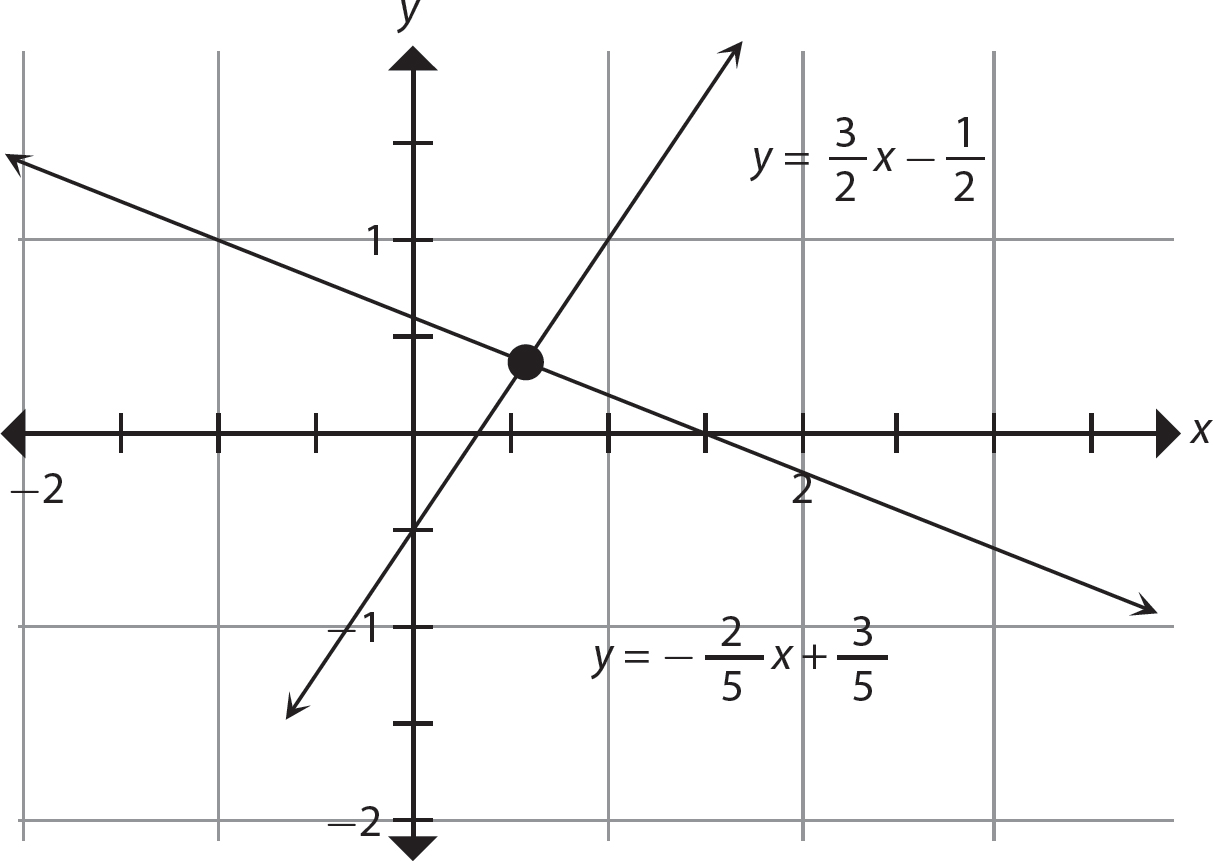
You can find an approximate solution of x ≈ 0.579 and y ≈ 0.368 by using a graphing utility. These values are close estimates but will not exactly satisfy either equation. Of course, you can find the exact solution of 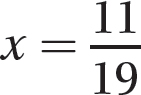and 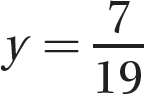by using either the substitution method or the elimination method. Nevertheless, the graphical approach gives you the approximate location of the intercept (if any), and, more important, this method helps you see the connection between the solution and the graphs of the two equations.

When an exact solution is needed, do not use the graphing method for solving a system of equations.

Exercise 20

For 1–3, solve by the substitution method.

1.

2.

3.

For 4–6, solve by the elimination method.

4.

5.

6.

For 7 and 8, estimate solutions by using the graphing method.

7.

8.