18

The Equation of a Line

In this chapter, you determine the equation of a line. The basic graph of all of mathematics is the straight line. It is the simplest to draw, and it has the unique property that it is completely determined by just two distinct points. Because of this unique property, it is a simple matter to write the equation of a line given just two items of critical information.

There are three common methods for determining the equation of a line.

Determining the Equation of a Line Given the Slope and y-Intercept

The simplest of the methods for determining the equation of a line is to use the slope-y-intercept form of the equation of a line: y = mx + b.

Problem   Given the slope m = 3 and the y-intercept = 5, write the equation of the line.

Solution

Step 1.   Recalling that the slope-y-intercept form of the equation of a line is y = mx + b, write the equation.

The equation of the line is y = 3x + 5. (You can see why this is the simplest method!)

Problem   Given the slope 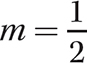and the y-intercept = −2, write the equation of the line.

Solution

Step 1.   Recalling that the slope-y-intercept form of the equation of a line is y = mx + b, write the equation.

The equation of the line is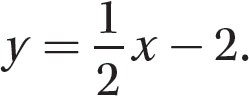

Determining the Equation of a Line Given the Slope and One Point on the Line

Use the point-slope formula 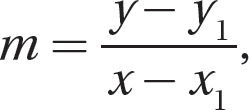, when you have the slope m and a point (x₁, y₁) on the line.

Watch your signs when you use the point-slope formula.

Problem   Given the slope m = 2 and a point (3, 2) on the line, write the equation of the line.

Solution

Step 1.   Let (x, y) be a point on the line different from (3, 2), then substitute the given information into the point-slope formula: .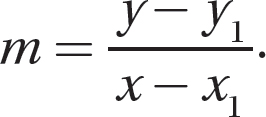

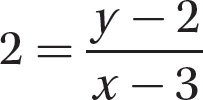
Step 2.   Solve the equation for y to get the slope-y-intercept form of the equation.

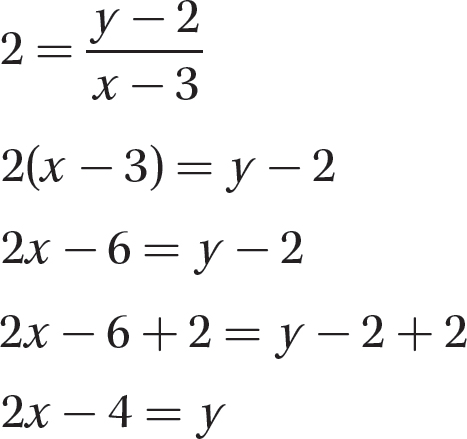
Step 3.   State the equation.

y = 2x−4 is the equation of the line.

Problem   Given the slope 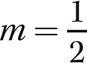and a point (−1, 3) on the line, write the equation of the line.

Solution

Step 1.   Let (x, y) be a point on the line different from (−1, 3), then substitute the given information into the point-slope formula: .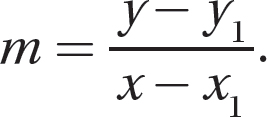

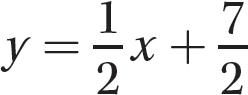
Step 2.   Solve the equation for y to get the slope-y-intercept form of the equation.

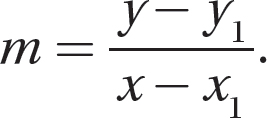
Step 3.   State the equation.

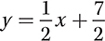is the equation of the line.

Problem   Given the slope m = −2 and a point (0, 0) on the line, write the equation of the line.

Solution

Step 1.   Let (x, y) be a point on the line different from (0, 0), then substitute the given information into the point-slope formula: .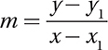

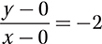
Step 2.   Solve the equation for y to get the slope-y-intercept form of the equation.

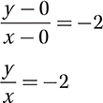
Step 3.   State the equation.

y = −2x is the equation of the line.

Determining the Equation of a Line Given Two Distinct Points on the Line

You also use the point-slope formula with this method.

Problem   Given the points (3, 4) and (1, 2) on the line, write the equation of the line.

Solution

Step 1.   Use the two points to determine the slope of the line.

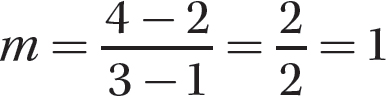
Step 2.   Now use the point-slope formula and one of the given points to finish writing the equation. Let (x, y) be a point on the line different from, say, (3, 4).

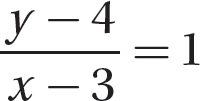
Step 3.   Solve the equation for y to get the slope-y-intercept form of the equation.

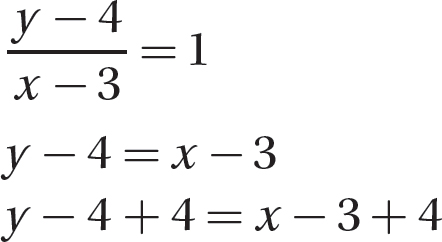
Step 4.   State the equation.

y = x + 1 is the equation of the line.

Problem   Given the points (−1, 4) and (3, −7) on the line, write the equation of the line.

Solution

Step 1.   Use the two points to determine the slope of the line.

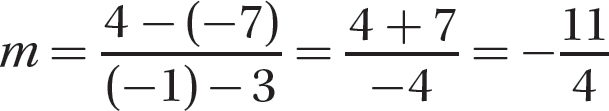
Step 2.   Now use the point-slope formula and one of the given points to finish writing the equation. Let (x, y) be a point on the line different from, say, (3, −7).

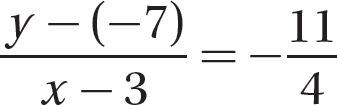
Step 3.   Solve the equation for y to get the slope-y-intercept form of the equation.

When two points are known, it does not make any difference which one is chosen to finish writing the equation.

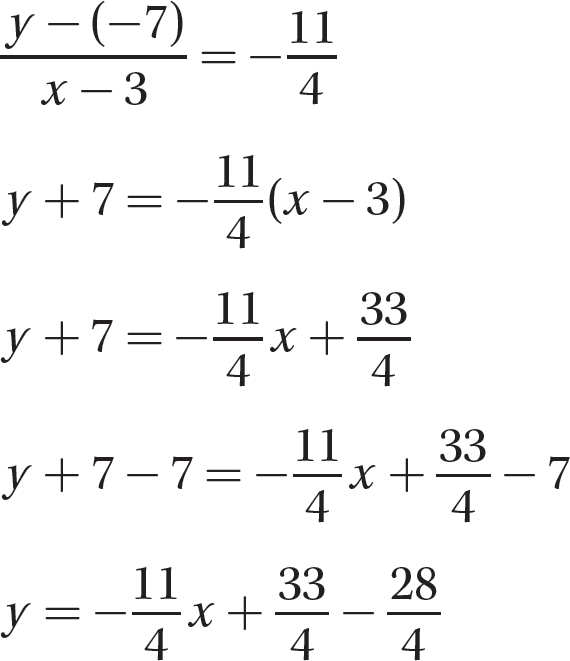
Step 4.   State the equation.

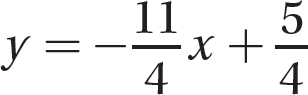is the equation of the line.

Exercise 18

1. Given the slope m = 4 and the y-intercept = 3, write the equation of the line.

2. Given the slope m = −3and the y-intercept = −3, write the equation of the line.

3. Given the slope 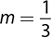and the y-intercept = 0, write the equation of the line.

4. Given the slope m = 2and a point (1, 1) on the line, write the equation of the line.

5. Given the slope m = −1and a point (2, 3) on the line, write the equation of the line.

6. Given the slope 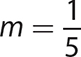and a point (0, 1) on the line, write the equation of the line.

7. Given the points (2, 4) and (1, 2) on the line, write the equation of the line.

8. Given the points (−1, 2) and (1, 2) on the line, write the equation of the line.

9. Given the points (2, −1) and (1, 0) on the line, write the equation of the line.

10. Given the points (4, 4) and (6, 6) on the line, write the equation of the line.