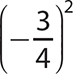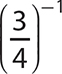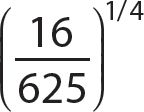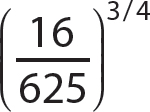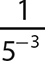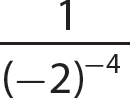This chapter presents a detailed discussion of exponents. Working efficiently and accurately with exponents will serve you well in algebra.
Exponents
An exponent is a small raised number written to the upper right of a quantity, which is called the base for the exponent. For example, consider the product 3 · 3 · 3 · 3 · 3, in which the same number is repeated as a factor multiple times. The shortened notation for 3 · 3 · 3 · 3 · 3 is 35. This representation of the product is an exponential expression. The number 3 is the base, and the small 5 to the upper right of 3 is the exponent. Most commonly, the exponential expression 35 is read as “three to the fifth.” Other ways you might read 35 are “three to the fifth power” or “three raised to the fifth power.” In general, xn is “x to the nth,” “x to the nth power,” or “x raised to the nth power.”
Exponentiation is the act of evaluating an exponential expression, xn.
The result you get is the nth power of the base. For instance, to evaluate 35, which has the natural number 5 as an exponent, perform the multiplication as shown here (see Figure 4.1).

Step 1. Write 35 in product form.
35 = 3 · 3 · 3 · 3 · 3
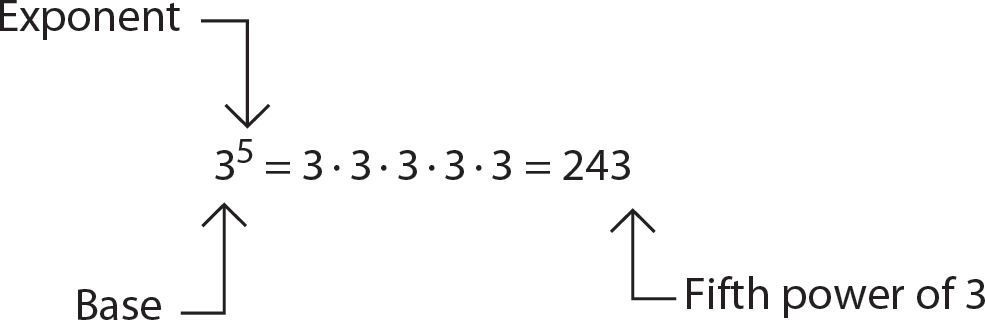
Figure 4.1 Parts of an exponential form
Step 2. Do the multiplication.
35 = 3 · 3 · 3 · 3 · 3 = 243 (the fifth power of 3)
The following discussion tells you about the different types of exponents and what they tell you to do to the base.
Natural Number Exponents
You likely are most familiar with natural number exponents.

Natural Number Exponents
If x is a real number and n is a natural number, then 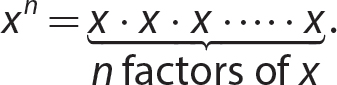
For instance, 54 has a natural number exponent, namely, 4. The exponent 4 tells you how many times to use the base 5 as a factor. When you do the exponentiation, the product is the fourth power of 5, as shown in Figure 4.2.
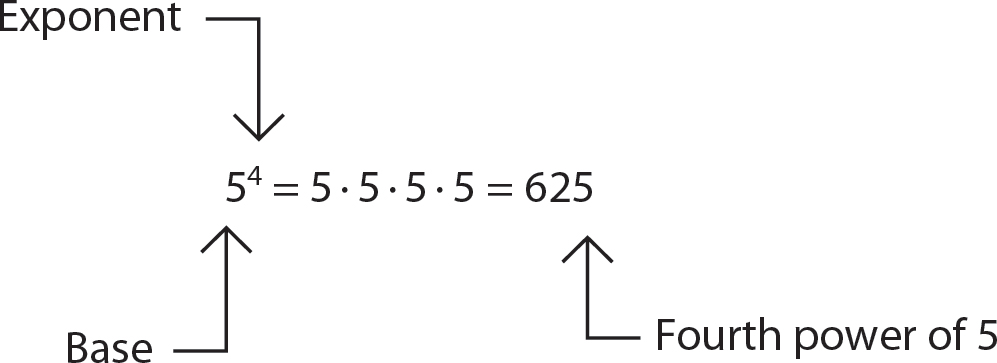
Figure 4.2 Fourth power of 5
For the first power of a number, for instance, 51, you usually omit the exponent and simply write 5. The second power of a number is the square of the number; read 52 as “five squared.” The third power of a number is the cube of the number; read 53 as “five cubed.” Beyond the third power, read 54 as “five to the fourth,” read 55 as “five to the fifth,” read 56 as “five to the sixth,” and so on.
Problem Write the indicated product as an exponential expression.
a. 2 · 2 · 2 · 2 · 2 · 2 · 2
b. −3 · −3 · −3 · −3 · −3 · −3
Solution
a. 2 · 2 · 2 · 2 · 2 · 2 · 2

Step 1. Count how many times 2 is a factor.
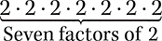
Step 2. Write the indicated product as an exponential expression with 2 as the base and 7 as the exponent.
2 · 2 · 2 · 2 · 2 · 2 · 2 = 27
b. −3 · −3 · −3 · −3 · −3 · −3

Step 1. Count how many times −3 is a factor.
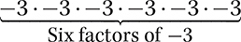
Step 2. Write the indicated product as an exponential expression with −3 as the base and 6 as the exponent.
−3 · −3 · −3 · −3 · −3 · −3 = (−3)6
In the above problem, you must enclose the −3 in parentheses to show that −3 is the number that is used as a factor six times. Only the 3 will be raised to the power unless parentheses are used to indicate otherwise.
Problem Evaluate.
a. 25
b. (−2)5
c. (0.6)2
d. 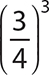
e. 0100
f. −52
g. (1 + 1)3
Solution
a. 25

Step 1. Write 25 in product form.
25 = 2 · 2 · 2 · 2 · 2
Step 2. Do the multiplication.
25 = 2 · 2 · 2 · 2 · 2 = 32
b. (−2)5

Step 1. Write (−2)5 in product form.
(−2)5 = −2 · −2 · −2 · −2 · −2
Step 2. Do the multiplication.
(−2)5 = −2 · −2 · −2 · −2 · −2 = −32
c. (0.6)2

Step 1. Write (0.6)2 in product form.
(0.6)2 = (0.6)(0.6)
Step 2. Do the multiplication.
(0.6)2 = (0.6)(0.6) = 0.36
d. 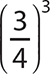

Step 3. Write 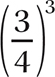 in product form.
in product form.
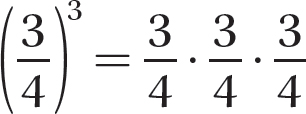
Step 2. Do the multiplication.
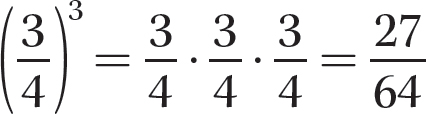
e. 0100

Step 1. Because 0100 has 0 as a factor 100 times, the product is 0.
0100 = 0
f. −52

Step 1. Keep the − symbol in front and write 52 in product form.
−52 = −5 · 5
Step 2. Do the multiplication.
−52 = −5 · 5 = −25
g. (1 + 1)3

Step 1. Add 1 and 1 because you want to cube the quantity 1 + 1. (See Chapter 5 for a discussion of parentheses as a grouping symbol.)
(1 + 1)3 = 23
Step 2. Write 23 in product form.
23 = 2 · 2 · 2
Step 3. Do the multiplication.
23 = 2 · 2 · 2 = 8
Zero and Negative Integer Exponents

Zero Exponent
If x is a nonzero real number, then x0 = 1.
A zero exponent on a nonzero number tells you to put 1 as the answer when you evaluate.
Problem Evaluate.
a. (−2)0
b. (0.6)0
c. 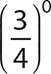
d. π0
e. 10
Solution
a. (−2)0

Step 1. The exponent is 0, so the answer is 1.
(−2)0 = 1
b. (0.6)0

Step 1. The exponent is 0, so the answer is 1.
(0.6)0 = 1
c. 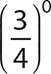

Step 1. The exponent is 0, so the answer is 1.
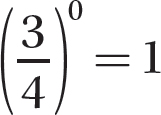
d. π0

Step 1. The exponent is 0, so the answer is 1.
π0 = 1
e. 10

Step 1. The exponent is 0, so the answer is 1.
10 = 1

Negative Integer Exponents
If x is a nonzero real number and n is a natural number, then 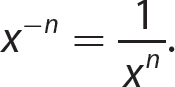 .
.
A negative integer exponent on a nonzero number tells you to obtain the reciprocal of the corresponding exponential expression that has a positive exponent.
Problem Evaluate.
a. 2−5
b. (−2)−5
c. (0.6)−2
d. 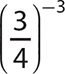
Solution
a. 2−5

Step 1. Write the reciprocal of the corresponding positive exponent version of 2−5.

Step 2. Evaluate 25.
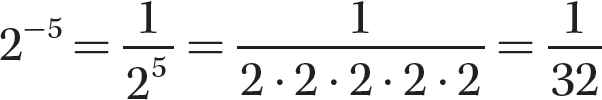
b. (−2)−5

Step 1. Write the reciprocal of the corresponding positive exponent version of (−2)−5.
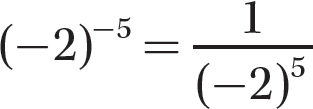
Step 2. Evaluate (−2)5.
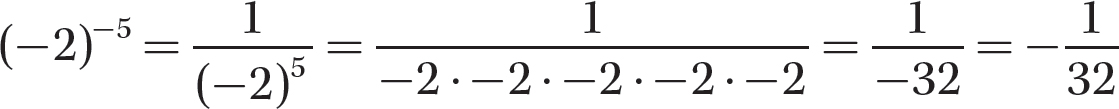
c. (0.6)−2

Step 1. Write the reciprocal of the corresponding positive exponent version of (0.6)−2.
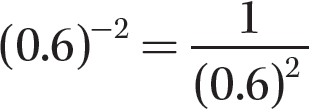
Step 2. Evaluate (0.6)2.
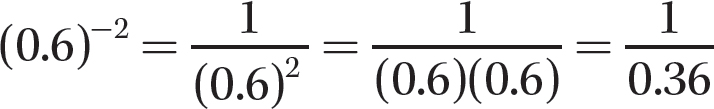
d. 

Step 1. Write the reciprocal of the corresponding positive exponent version of  .
.

Step 2. Evaluate  and simplify.
and simplify.
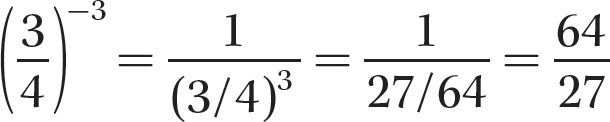
Notice that because 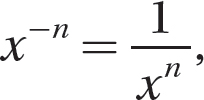 , the expression
, the expression 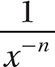 can be simplified as follows:
can be simplified as follows:
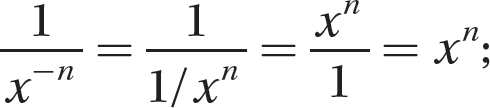 thus,
thus, 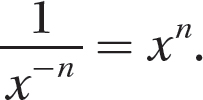 . Apply this rule in the following problem.
. Apply this rule in the following problem.
Problem Simplify.
a. 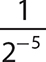
b. 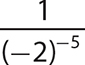
c. 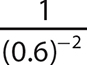
Solution
a. 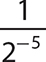

Step 1. Apply 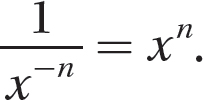
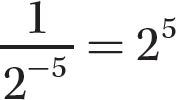
Step 2. Evaluate 25.
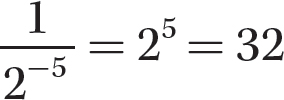
b. 

Step 1. Apply 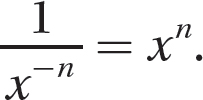
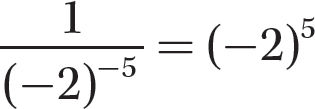
Step 2. Evaluate (−2)5.
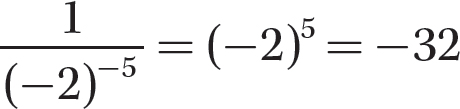
c. 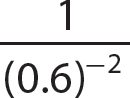

Step 1. Apply 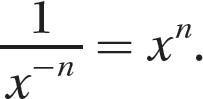
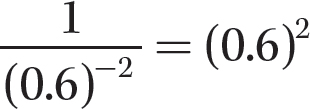
Step 2. Evaluate (0.6)2.
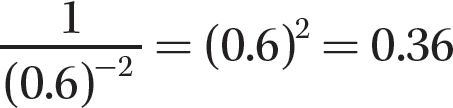
Unit Fraction and Rational Exponents

Unit Fraction Exponents
If x is a real number and n is a natural number, then 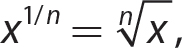 , provided that, when n is even, x ≥ 0.
, provided that, when n is even, x ≥ 0.
A unit fraction exponent on a number tells you to find the principal nth root of the number.
Problem Evaluate, if possible.
a. (−27)1/3
b. (0.25)1/2
c. (−16)1/4
d. 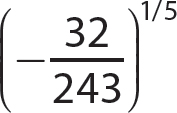
Solution
a. (−27)1/3

Step 1. Apply 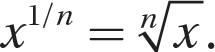
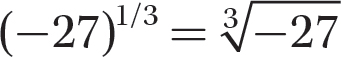
Step 2. Find the principal cube root of −27.

b. (0.25)1/2

Step 1. Apply 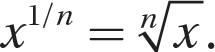
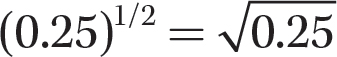
Step 2. Find the principal square root of 0.25.
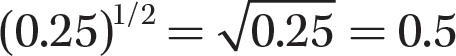
c. (−16)1/4

Step 1. Apply 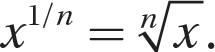
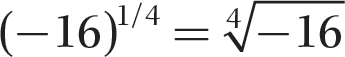
Step 2. −16 is negative and 4 is even, so (−16)1/4 is not a real number.
 is not defined for real numbers.
is not defined for real numbers.
d. 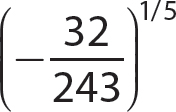

Step 1. Apply 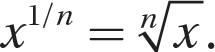
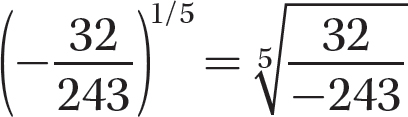
Step 2. Find the principal fifth root of 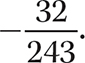
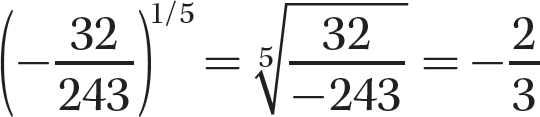

Rational Exponents
If x is a real number and m and n are natural numbers, then (a) xm/n = (x1/n)m or (b) xm/n = (xm)1/n, provided that in all cases even roots of negative numbers do not occur.
When you evaluate the exponential expression xm/n, you can find the nth root of x first and then raise the result to the mth power, or you can raise x to the mth power first and then find the nth root of the result. For most numerical situations, you usually will find it easier to find the root first and then raise to the power (as you will observe from the sample problems shown here).
Problem Evaluate using xm/n = (x1/n)m.
a. 
b. (36)3/2
Solution
a. 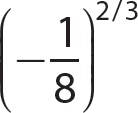

Step 1. Rewrite 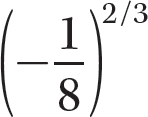 using xm/n = (x1/n)m.
using xm/n = (x1/n)m.
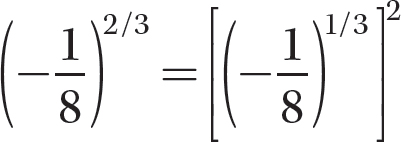
Step 2. Find 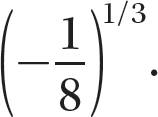 .
.
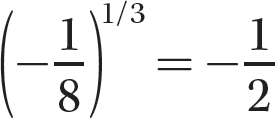
Step 3. Raise 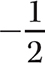 to the second power.
to the second power.
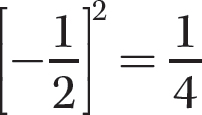
Step 4. Review your main results.

b. (36)3/2

Step 1. Rewrite (36)3/2 using xm/n = (x1/n)m.
(36)3/2 = (361/2)3
Step 2. Find (36)1/2.
(36)1/2 = 6
Step 3. Raise 6 to the third power.
63 = 216
Step 4. Review your main results.
(36)3/2 = (361/2)3 = 63 = 216
Problem Evaluate using xm/n = (xm)1/n.
a. 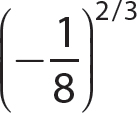
b. (36)3/2
Solution
a. 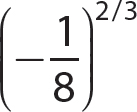

Step 1. Rewrite 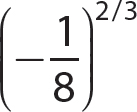 using xm/n = (xm)1/n.
using xm/n = (xm)1/n.
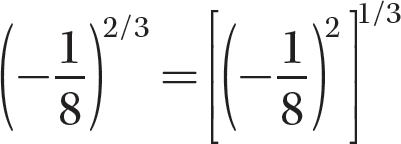
Step 2. Find 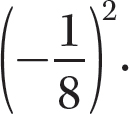
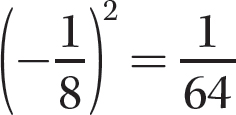
Step 3. Find 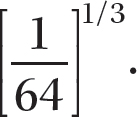

Step 4. Review your main results.
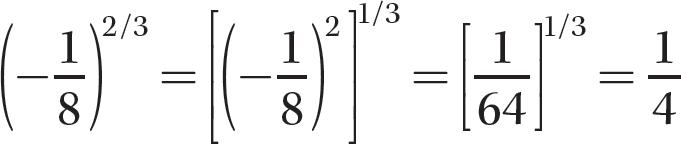
b. (36)3/2

Step 1. Rewrite (36)3/2 using xm/n = (xm)1/n.
(36)3/2 = (363)1/2
Step 2. Find (36)3.
(36)3 = 46,656
Step 3. Find (46,656)1/2.
(46,656)1/2 = 216
Step 4. Review your main results.
(36)3/2 = (363)1/2 = (46,656)1/2 = 216
Exercise 4

For 1 and 2, write the indicated product as an exponential expression.
1. −4 ·−4 ·−4 ·−4 ·−4
2. 8 · 8 · 8 · 8 · 8 · 8 · 8
For 3–18, evaluate, if possible.
3. (−2)7
4. (0.3)4
6. −24
7. (1 + 1)4
8. (−2)0
9. 3−4
10. (−4)−2
11. (0.3)−2
13. (−125)1/3
14. (0.16)1/2
15. (−121)1/4
17. (−27)2/3
For 19 and 20, simplify.
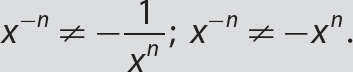 A negative exponent does not make a power negative.
A negative exponent does not make a power negative.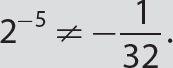
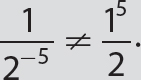 Keep the same base for the corresponding positive exponent version.
Keep the same base for the corresponding positive exponent version. , and so forth.
, and so forth.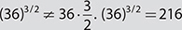 , but
, but 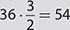 . Don’t multiply the base by the exponent!
. Don’t multiply the base by the exponent!