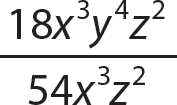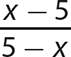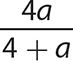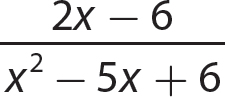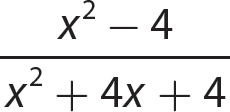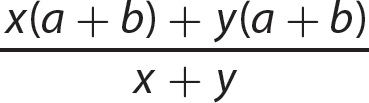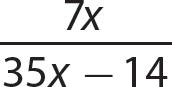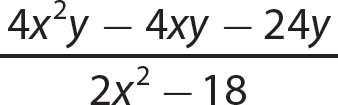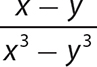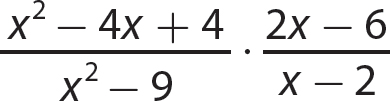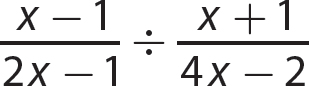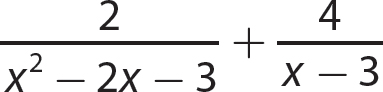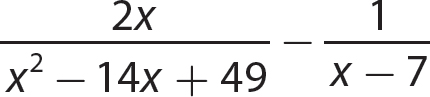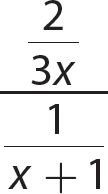In this chapter, you apply your skills in factoring polynomials to the charge of simplifying rational expressions. A rational expression is an algebraic fraction that has a polynomial for its numerator and a polynomial for its denominator. For instance, 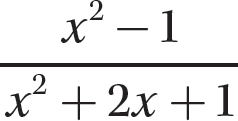 is a rational expression. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the denominator polynomial evaluate to 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
is a rational expression. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the denominator polynomial evaluate to 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
Reducing Algebraic Fractions to Lowest Terms
The following principle is fundamental to rational expressions.

Fundamental Principle of Rational Expressions
If P, Q, and R are polynomials, then 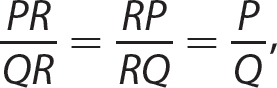 , provided neither Q nor R has a zero value.
, provided neither Q nor R has a zero value.
The fundamental principle allows you to reduce algebraic fractions to lowest terms by dividing the numerator and denominator by the greatest common factor (GCF).
Problem Reduce to lowest terms.
a. 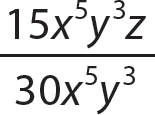
b. 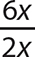
c. 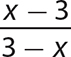
d. 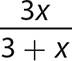
e. 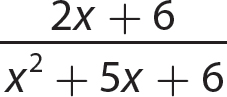
f. 
g. 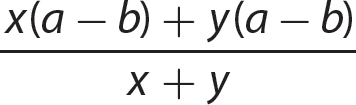
Solution
a. 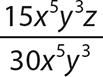

Step 1. Determine the GCF for 15x5y3z and 30x5y3.
GCF = 15 x5y3
Step 2. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
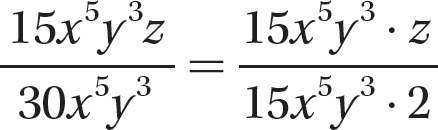
Step 3. Use the fundamental principle to reduce.
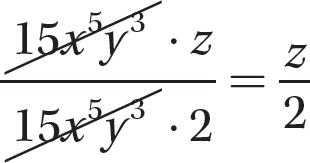
b. 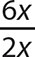

Step 1. Determine the GCF for 6x and 2x.
GCF = 2 x
Step 2. Write the numerator and denominator as equivalent products with the GCF as one of the factors.

Step 3. Use the fundamental principle to reduce the fraction.
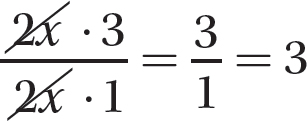
c. 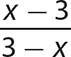

Step 1. Factor −1 from the denominator polynomial, so that the x term will have a positive coefficient.
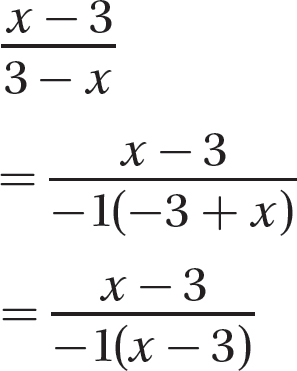
Step 2. Determine the GCF for x − 3 and −1(x − 3).
GCF = (x − 3) (Enclose x − 3 in parentheses to emphasize it’s a factor.)
Step 3. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
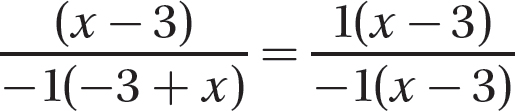
Step 4. Use the fundamental principle to reduce the fraction.

d. 

Step 1. Determine the GCF for 3x and 3 + x.
GCF = 1, so 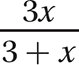 cannot be reduced further.
cannot be reduced further.
e. 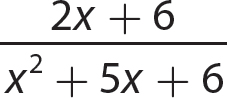

Step 1. Factor the numerator and denominator polynomials completely.
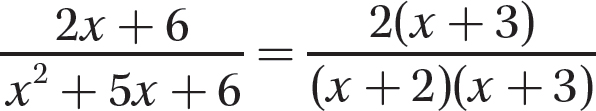
Step 2. Determine the GCF for 2(x + 3) and (x + 2)(x + 3).
GCF = (x + 3)
Step 3. Use the fundamental principle to reduce the fraction (in Step 1).

f. 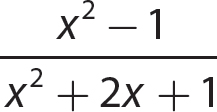

Step 1. Factor the numerator and denominator polynomials completely.
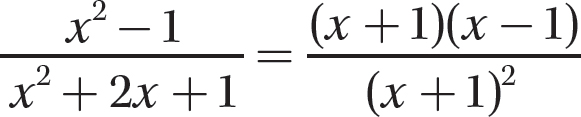
Step 2. Determine the GCF for (x + 1)(x − 1) and (x + 1)2.
GCF = (x + 1)
Step 3. Write the numerator and denominator as equivalent products with the GCF as one of the factors.

Step 4. Use the fundamental principle to reduce the fraction.
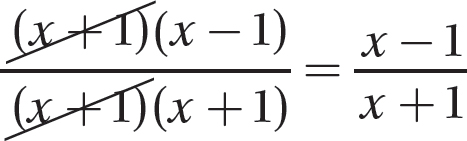
g. 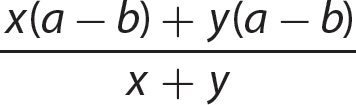

Step 1. Factor the numerator and denominator polynomials completely.
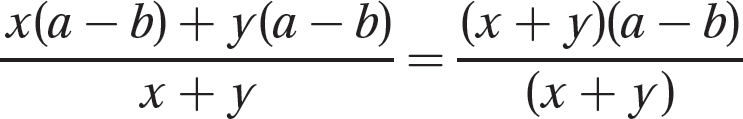
Step 2. Determine the GCF for (x + y)(a − b) and (x + y).
GCF = (x + y)
Step 3. Use the fundamental principle to reduce the fraction (in Step 1).
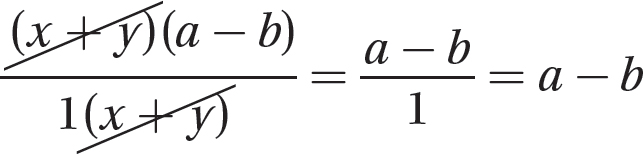
Multiplying Algebraic Fractions
To multiply algebraic fractions, (1) factor all numerators and denominators completely, (2) divide numerators and denominators by their common factors (as in reducing), and (3) multiply the remaining numerator factors to get the numerator of the answer and multiply the remaining denominator factors to get the denominator of the answer.
Problem Find the product.
a. 
b. 
Solution
a. 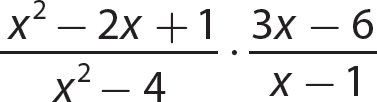

Step 1. Factor all numerators and denominators completely.
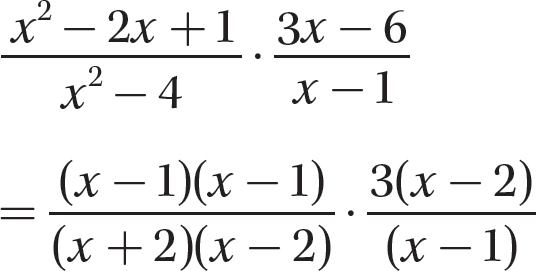
Step 2. Divide out common numerator and denominator factors.
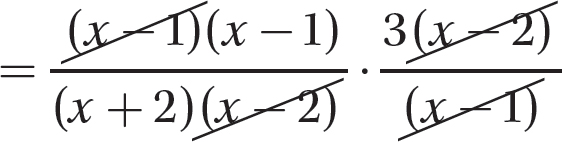
Step 3. Multiply the remaining numerator factors to get the numerator of the answer and multiply the remaining denominator factors to get the denominator of the answer.
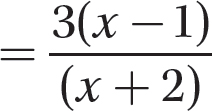
Step 4. Review the main steps.
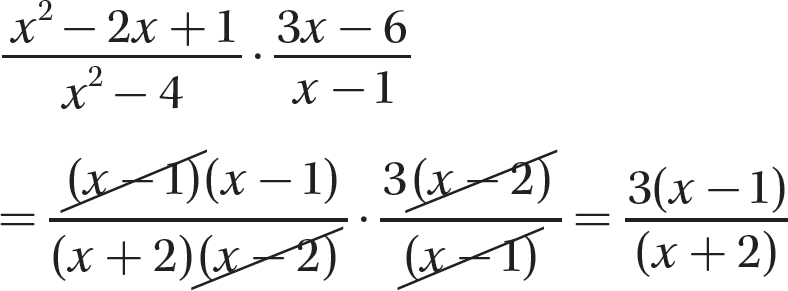
b. 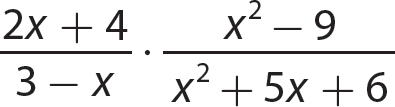

Step 1. Factor all numerators and denominators completely.

Step 2. Divide out common numerator and denominator factors.
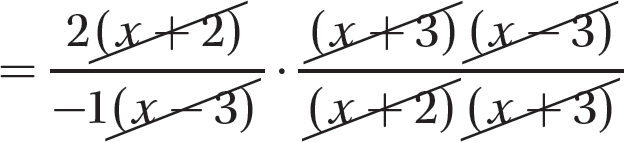
Step 3. Multiply the remaining numerator factors to get the numerator of the answer, and multiply the remaining denominator factors to get the denominator of the answer.

Step 4. Review the main steps.
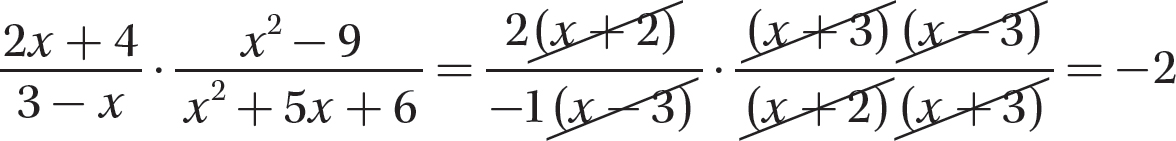
Dividing Algebraic Fractions
To divide algebraic fractions, multiply the first algebraic fraction by the reciprocal of the second algebraic fraction (the divisor).
Problem Find the quotient: 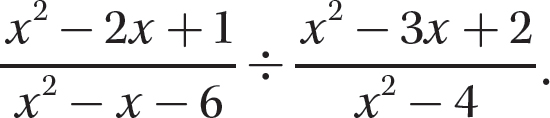 .
.
Solution

Step 1. Change the problem to multiplication by the reciprocal of the divisor.
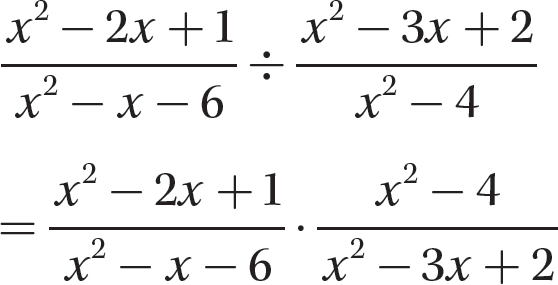
Step 2. Factor all numerators and denominators completely.
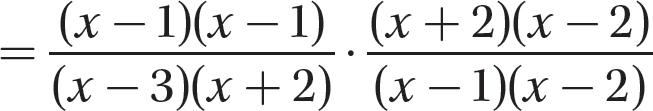
Step 3. Divide out common numerator and denominator factors.
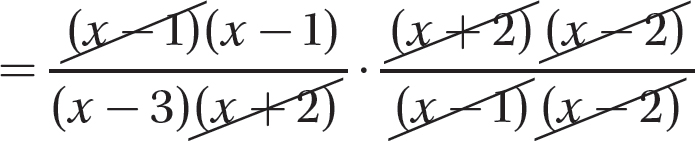
Step 4. Multiply the remaining numerator factors to get the numerator of the answer, and multiply the remaining denominator factors to get the denominator of the answer.

Step 5. Review the main steps.
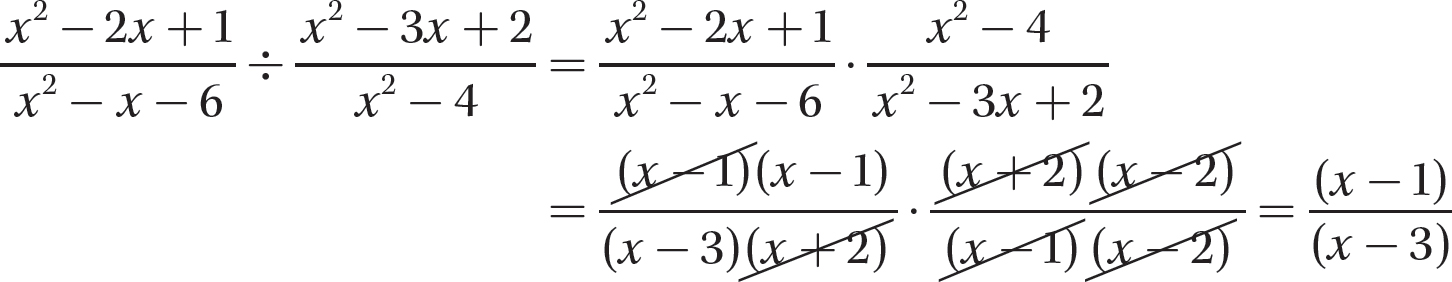
Adding (or Subtracting) Algebraic Fractions, Like Denominators
To add (or subtract) algebraic fractions that have like denominators, place the sum (or difference) of the numerators over the common denominator. Simplify and reduce to lowest terms, if needed.
Problem Compute as indicated.
a. 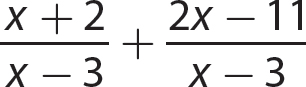
b. 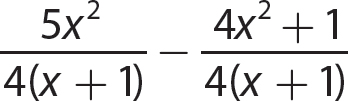
Solution
a. 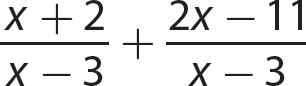

Step 1. Indicate the sum of the numerators over the common denominator.
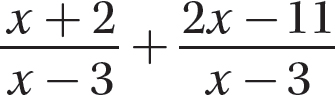
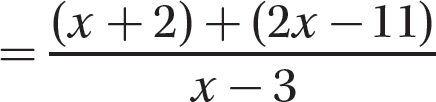
Step 3. Find the sum of the numerators.
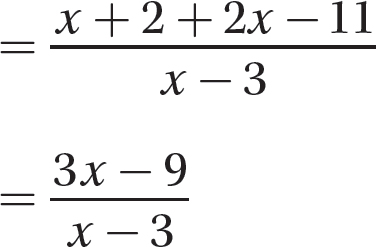
Step 3. Reduce to lowest terms.
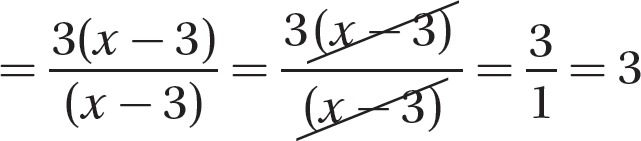
Step 4. Review the main steps.
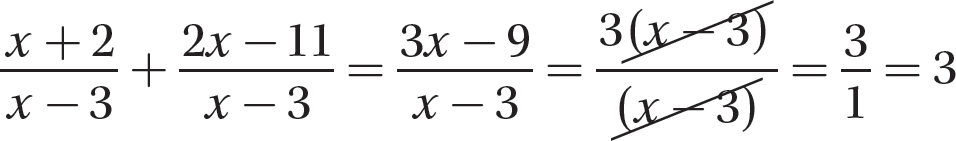
b. 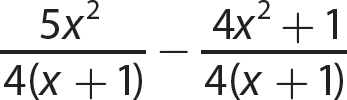

Step 1. Indicate the difference of the numerators over the common denominator.
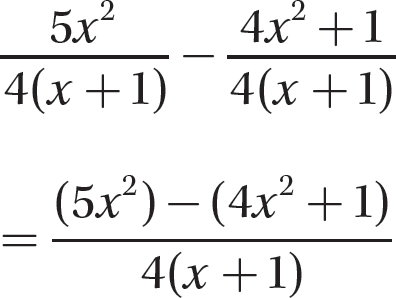
Step 2. Find the difference of the numerators.
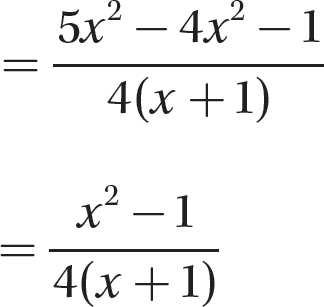
Step 3. Reduce to lowest terms.
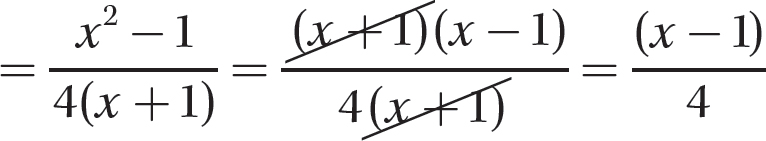
Step 4. Review the main steps.
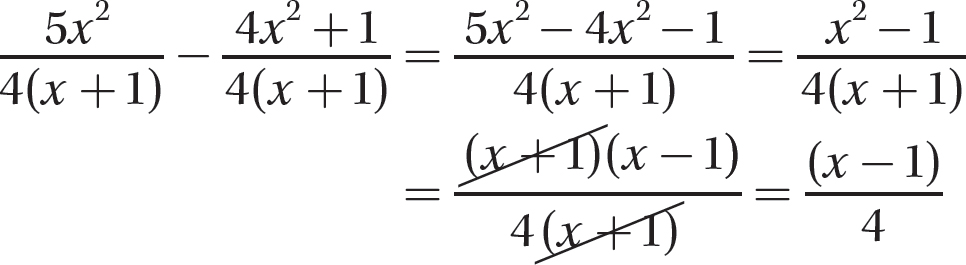
Adding (or Subtracting) Algebraic Fractions, Unlike Denominators
To add (or subtract) algebraic fractions that have unlike denominators, (1) factor each denominator completely; (2) find the least common denominator (LCD), which is the product of each prime factor the highest number of times it is a factor in any one denominator; (3) using the fundamental principle, write each algebraic fraction as an equivalent fraction having the common denominator as a denominator; and (4) add (or subtract) as for like denominators.
Note: A prime factor is one that cannot be factored further.
Problem Compute as indicated.
a. 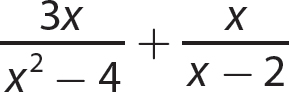
b. 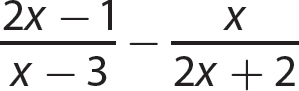
Solution
a. 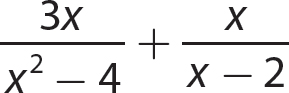

Step 1. Factor each denominator completely.
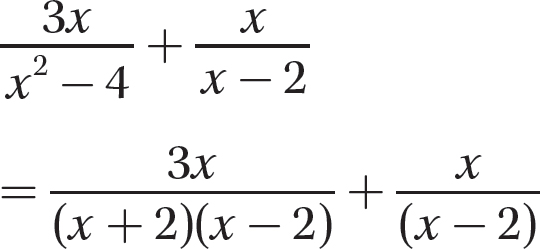
Step 2. Find the LCD.
LCD = (x + 2)(x−2)
Step 3. Write each algebraic fraction as an equivalent fraction having the common denominator as a denominator.
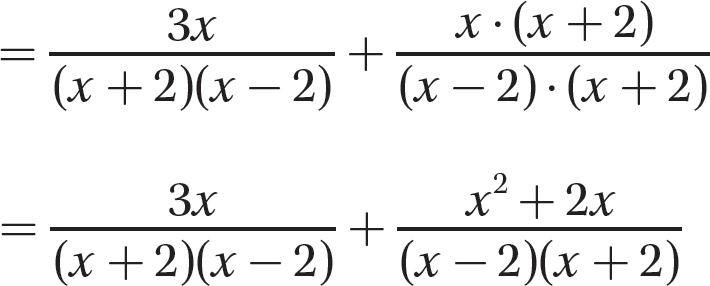
Step 4. Add as for like denominators.
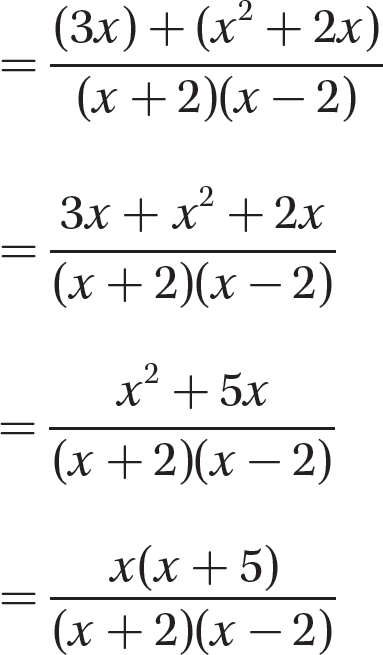
Step 5. Review the main steps.
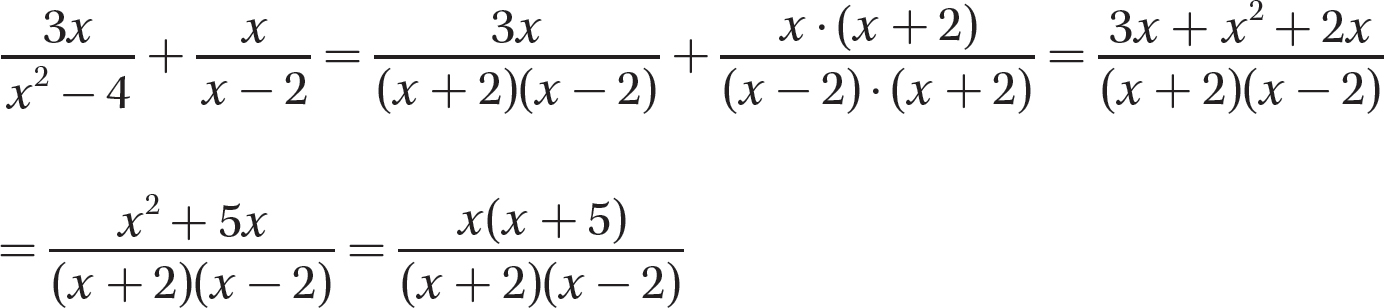
b. 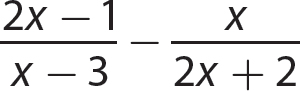

Step 1. Factor each denominator completely.
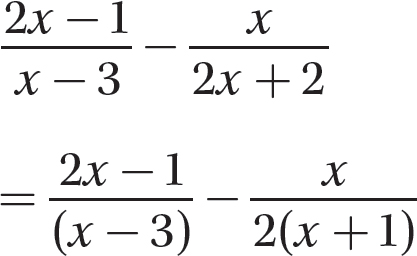
Step 2. Find the LCD.
LCD = 2(x−3)(x + 1)
Step 3. Write each algebraic fraction as an equivalent fraction having the common denominator as a denominator.
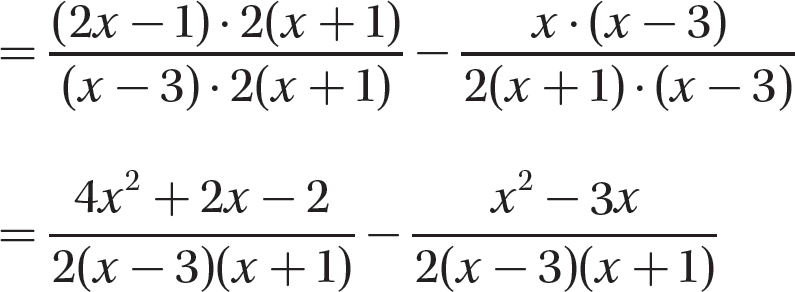
Step 4. Subtract as for like denominators.
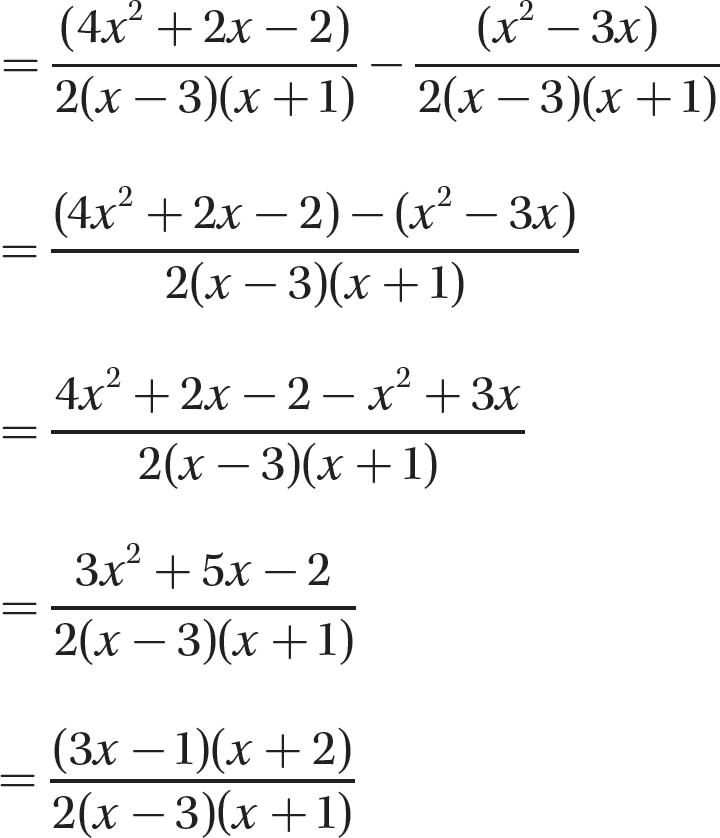
Step 5. Review the main steps.
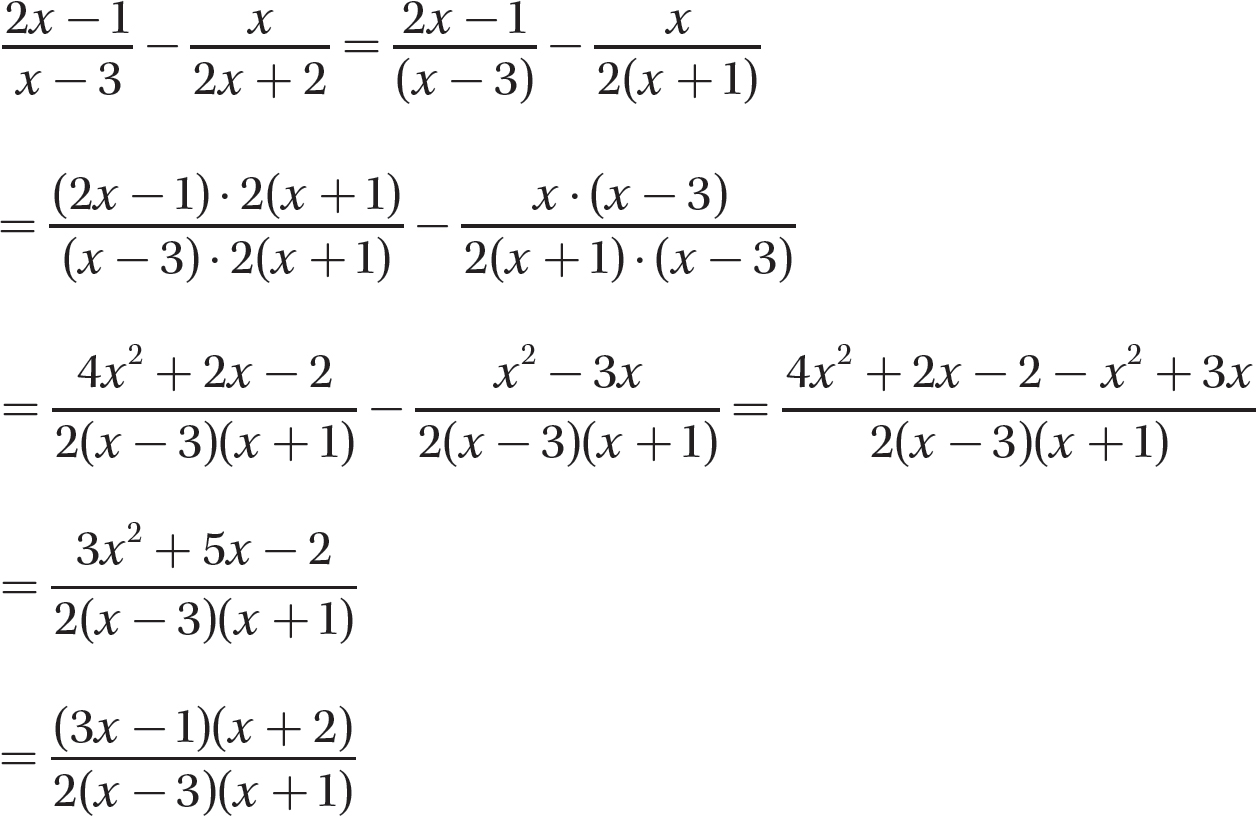
Simplifying Complex Fractions
A complex fraction is a fraction that has fractions in its numerator, denominator, or both. One way you can simplify a complex fraction is to interpret the fraction bar of the complex fraction as meaning division.
Problem Simplify: 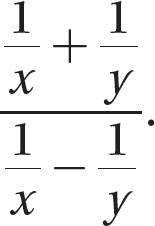
Solution

Step 1. Write the complex fraction as a division problem.
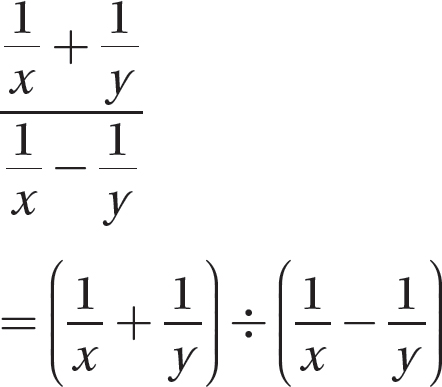
Step 2. Perform the indicated addition and subtraction.
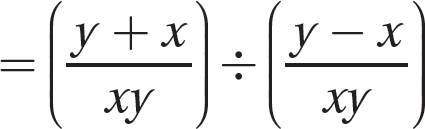
Step 3. Multiply by the reciprocal of the divisor.
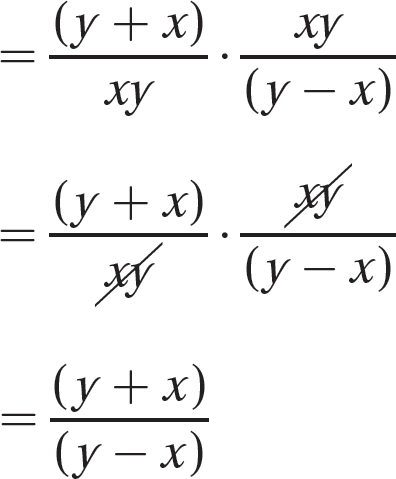
Step 4. Review the main steps.
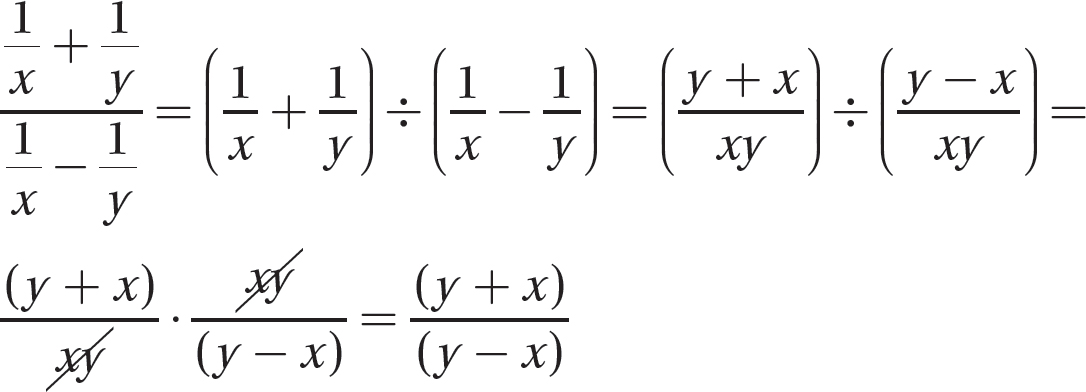
Another way you can simplify a complex fraction is to multiply its numerator and denominator by the LCD of all the fractions in its numerator and denominator.
Problem Simplify: 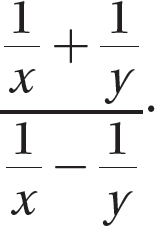
Solution

Step 1. Multiply the numerator and denominator by the LCD of all the fractions.

Exercise 13

For 1–10, reduce to lowest terms.
For 11–15, compute as indicated.
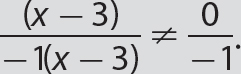 . Think of (x − 3) as 1(x − 3).
. Think of (x − 3) as 1(x − 3). . 3 is a factor of the numerator, but it is a term of the denominator. It is a mistake to divide out a term.
. 3 is a factor of the numerator, but it is a term of the denominator. It is a mistake to divide out a term. . 6 is a common term in the numerator and denominator, not a factor. Only divide out factors.
. 6 is a common term in the numerator and denominator, not a factor. Only divide out factors.