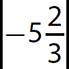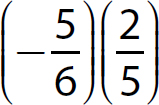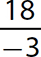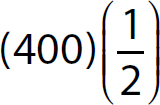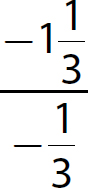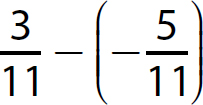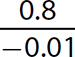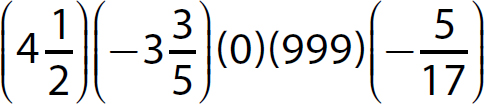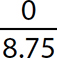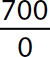This chapter presents the rules for computing with real numbers—often called signed numbers. Before proceeding with addition, subtraction, multiplication, and division of signed numbers, the discussion begins with comparing numbers and finding the absolute value of a number.
Comparing Numbers and Absolute Value
Comparing numbers uses the inequality symbols shown in Table 2.1.
Table 2.1 Inequality Symbols

Graphing the numbers on a number line is helpful when you compare two numbers. The number that is farther to the right is the greater number. If the numbers coincide, they are equal; otherwise, they are unequal.
Problem Which is greater, −7 or −2?
Solution

Step 1. Graph −7 and −2 on a number line.
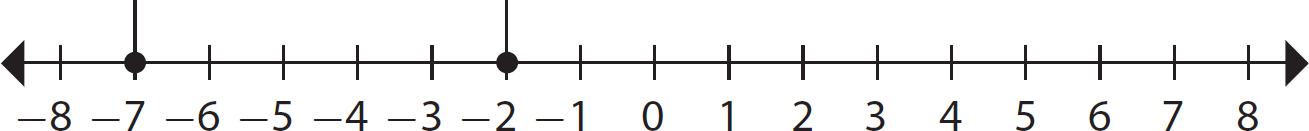
Step 2. Identify the number that is farther to the right as the greater number.
−2 is to the right of −7, so −2 > −7.
The concept of absolute value plays an important role in computations with signed numbers. The absolute value of a real number is its distance from 0 on the number line. For example, as shown in Figure 2.1, the absolute value of −8 is 8 because −8 is 8 units from 0.

Figure 2.1 The absolute value of −8
You indicate the absolute value of a number by placing the number between a pair of vertical bars like this: |−8| (read as “the absolute value of negative eight”). Thus, |−8| = 8.
Problem Find the indicated absolute value.
a. |−30|
b. |0.4|
c. 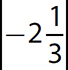
Solution
a. |−30|

Step 1. Recalling that the absolute value of a real number is its distance from 0 on the number line, determine the absolute value.
|−30| = 30 because −30 is 30 units from 0 on the number line.
b. |0.4|

Step 1. Recalling that the absolute value of a real number is its distance from 0 on the number line, determine the absolute value.
|0.4| = 0.4 because 0.4 is 0.4 unit from 0 on the number line.
c. 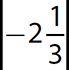

Step 1. Recalling that the absolute value of a real number is its distance from 0 on the number line, determine the absolute value.
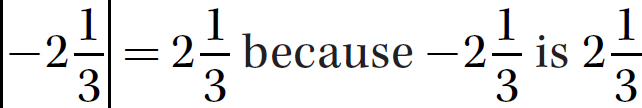 units from 0 on the number line.
units from 0 on the number line.
Problem Which number, if any, has the greater absolute value?
a. −35, 60
b. 35, −60
c. −25, 25
d. 
Solution
a. −35, 60

Step 1. Determine the absolute values.
|−35| = 35, |60| = 60
Step 2. Compare the absolute values.
60 has the greater absolute value because 60 > 35.
b. 35, −60

Step 1. Determine the absolute values.
|35| = 35, |−60| = 60
Step 2. Compare the absolute values.
−60 has the greater absolute value because 60 > 35.
c. −25, 25

Step 1. Determine the absolute values.
|−25| = 25, |25| = 25
Step 2. Compare the absolute values.
Neither number has the greater absolute value because 25 = 25.
d. 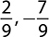

Step 1. Determine the absolute values.
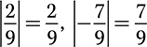
Step 2. Compare the absolute values.
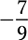 has the greater absolute value because
has the greater absolute value because 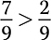 .
.
Addition and Subtraction of Signed Numbers
Real numbers are called signed numbers because these numbers may be positive, negative, or 0. From your knowledge of arithmetic, you already know how to do addition, subtraction, multiplication, and division with positive numbers and 0. To do these operations with all signed numbers, you simply use the absolute values of the numbers and follow the eight rules in this chapter.

Addition of Signed Numbers
Rule 1. To add two numbers that have the same sign, add their absolute values and give the sum their common sign.
Rule 2. To add two numbers that have opposite signs, subtract the lesser absolute value from the greater absolute value and give the sum the sign of the number with the greater absolute value; if the two numbers have the same absolute value, their sum is 0.
Rule 3. The sum of 0 and any number is the number.
Problem Find the sum.
a. −35 + −60
b. 35 + −60
c. −35 + 60
d. 
e. 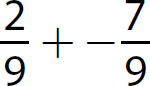
f. −9.75 + −8.12
g. −990.36 + 0
Solution
a. −35 + −60

Step 1. Determine which addition rule applies.
−35 + −60
The signs are the same (both negative), so use Rule 1.
Step 2. Add the absolute values, 35 and 60.
35 + 60 = 95
Step 3. Give the sum a negative sign (the common sign).
−35 + −60 = −95
b. 35 + −60

Step 1. Determine which addition rule applies.
35 + −60
The signs are opposites (one positive and one negative), so use Rule 2.
Step 2. Subtract 35 from 60 because |−60| > |35|.
60 − 35 = 25
Step 3. Make the sum negative because −60 has the greater absolute value.
35 + −60 = −25
c. −35 + 60

Step 1. Determine which addition rule applies.
−35 + 60
The signs are opposites (one negative and one positive), so use Rule 2.
Step 2. Subtract 35 from 60 because |60| > |−35|.
60 − 35 = 25
Step 3. Keep the sum positive because 60 has the greater absolute value.
−35 + 60 = 25
d. 

Step 1. Determine which addition rule applies.
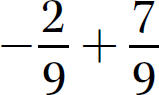
The signs are opposites (one positive and one negative), so use Rule 2.
Step 2. Subtract  from
from  because
because 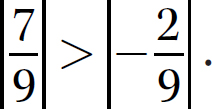 .
.
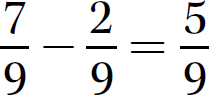
Step 3. Keep the sum positive because  has the greater absolute value.
has the greater absolute value.
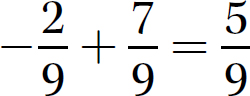
e. 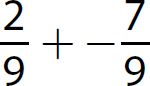

Step 1. Determine which addition rule applies.
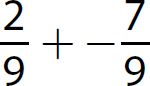
The signs are opposites (one positive and one negative), so use Rule 2.
Step 2. Subtract  from
from  because
because 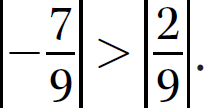 .
.

Step 3. Make the sum negative because 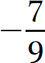 has the greater absolute value.
has the greater absolute value.
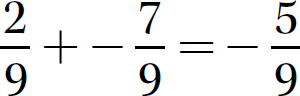
f. −9.75 + −8.12

Step 1. Determine which addition rule applies.
−9.75 + −8.12
The signs are the same (both negative), so use Rule 1.
Step 2. Add the absolute values 9.75 and 8.12.
9.75 + 8.12 = 17.87
Step 3. Give the sum a negative sign (the common sign).
−9.75 + −8.12 = −17.87
g. −990.36 + 0

Step 1. Determine which addition rule applies.
−990.36 + 0
0 is added to a number, so the sum is the number (Rule 3).
−990.36 + 0 = −990.36
You subtract signed numbers by changing the subtraction problem to an addition problem in a special way, so that you can apply the rules for addition of signed numbers. Here is the rule.

Subtraction of Signed Numbers
Rule 4. To subtract two numbers, keep the first number and add the opposite of the second number.
To apply this rule, think of the minus sign, −, as “add the opposite of.” In other words, “subtracting a number” and “adding the opposite of the number” give the same answer.
Problem Change the subtraction problem to an addition problem.
a. −35 − 60
b. 35 − 60
c. 60 − 35
d. −35 − (−60)
e. 0 − 60
f. −60 − 0
Solution
a. −35 − 60

Step 1. Keep −35.
−35
Step 2. Add the opposite of 60.
= −35 + −60
b. 35 − 60

Step 1. Keep 35.
35
Step 2. Add the opposite of 60.
= 35 + −60
c. 60 − 35

Step 1. Keep 60.
60
Step 2. Add the opposite of 35.
= 60 + −35
d. −35 − (−60)

Step 1. Keep −35.
−35
Step 2. Add the opposite of −60.
= −35 + 60
e. 0 − 60

Step 1. Keep 0.
0
Step 2. Add the opposite of 60.
= 0 + −60
f. −60 − 0

Step 1. Keep −60.
−60
Step 2. Add the opposite of 0.
= −60 + 0
Problem Find the difference.
a. −35 − 60
b. 35 − 60
c. 60 − 35
d. −35 − (−60)
e. 0 − (−60)
f. −60 − 0
Solution
a. −35 − 60

Step 1. Keep −35 and add the opposite of 60.
−35 − 60
= −35 + −60
Step 2. The signs are the same (both negative), so use Rule 1 for addition.
= −95
Step 3. Review the main results.
−35 − 60 = −35 + −60 = −95
a. 35 − 60

Step 1. Keep 35 and add the opposite of 60.
35 − 60
= 35 + −60
Step 2. The signs are opposites (one positive and one negative), so use Rule 2 for addition.
= −25
Step 3. Review the main results.
35 − 60 = 35 + −60 = −25
c. 60 − 35

Step 1. Keep 60 and add the opposite of 35.
60 − 35
= 60 + −35
Step 2. The signs are opposites (one positive and one negative), so use Rule 2 for addition.
= 25
Step 3. Review the main results.
60 − 35 = 60 + −35 = 25
d. −35 − (−60)

Step 1. Keep −35 and add the opposite of −60.
−35 − (−60)
= −35 + 60
Step 2. The signs are opposites (one positive and one negative), so use Rule 2 for addition.
= 25
Step 3. Review the main results.
−35 − (−60) = −35 + 60 = 25
e. 0 − (−60)

Step 1. Keep 0 and add the opposite of −60.
0 − (−60)
= 0 + 60
Step 2. 0 is added to a number, so the sum is the number (Rule 3 for addition).
= 60
Step 3. Review the main results.
0 − (−60) = 0 + 60 = 60
f. −60 − 0

Step 1. Keep −60 and add the opposite of 0.
−60 − 0
= −60 + 0
Step 2. 0 is added to a number, so the sum is the number (Rule 3 for addition).
= −60
Step 3. Review the main results.
−60 − 0 = −60 + 0 = −60
Before going on, it is important that you distinguish the various uses of the short horizontal − symbol. Thus far, this symbol has three uses: (1) as part of a number to show that the number is negative, (2) as an indicator to find the opposite of the number that follows, and (3) as the minus symbol indicating subtraction.
Problem Given the statement 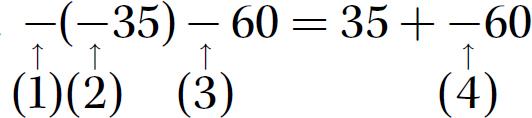
a. Describe the use of the − symbols at (1), (2), (3), and (4).
b. Express the statement −(−35) − 60 = 35 + −60 in words.
Solution
a. Describe the use of the − symbols at (1), (2), (3), and (4).

Step 1. Interpret each − symbol.

b. Express the statement −(−35) − 60 = 35 + −60 in words.

Step 1. Translate the statement into words.
−(−35) − 60 = 35 + −60 is read “the opposite of negative thirty-five minus sixty is thirty-five plus negative sixty.”
Multiplication and Division of Signed Numbers
For multiplication of signed numbers, use the following three rules:

Multiplication of Signed Numbers
Rule 5. To multiply two numbers that have the same sign, multiply their absolute values and keep the product positive.
Rule 6. To multiply two numbers that have opposite signs, multiply their absolute values and make the product negative.
Rule 7. The product of 0 and any number is 0.
Problem Find the product.
a. (−3)(−40)
b. (3)(40)
c. (−3)(40)
d. (3)(−40)
e. (358)(0)
Solution
a. (−3)(−40)

Step 1. Determine which multiplication rule applies.
(−3)(−40)
The signs are the same (both negative), so use Rule 5.
Step 2. Multiply the absolute values, 3 and 40.
(3)(40) = 120
Step 3. Keep the product positive.
(−3)(−40) = 120
b. (3)(40)

Step 1. Determine which multiplication rule applies.
(3)(40)
The signs are the same (both positive), so use Rule 5.
Step 2. Multiply the absolute values, 3 and 40.
(3)(40) = 120
Step 3. Keep the product positive.
(3)(40) = 120
c. (−3)(40)

Step 1. Determine which multiplication rule applies.
(−3)(40)
The signs are opposites (one negative and one positive), so use Rule 6.
Step 2. Multiply the absolute values, 3 and 40.
(3)(40) = 120
Step 3. Make the product negative.
(−3)(40) = −120
d. (3)(−40)

Step 1. Determine which multiplication rule applies.
(3)(−40)
The signs are opposites (one positive and one negative), so use Rule 6.
Step 2. Multiply the absolute values, 3 and 40.
(3)(40) = 120
Step 3. Make the product negative.
(3)(−40) = −120
e. (358)(0)

Step 1. Determine which multiplication rule applies.
(358)(0)
0 is one of the factors, so use Rule 7.
Step 2. Find the product.
(358)(0) = 0
Rules 5, 6, and 7 tell you how to multiply two numbers, but often you will want to find the product of more than two numbers. To do this, multiply in pairs. You can keep track of the sign as you go along, or you simply can use the following guideline:
When 0 is one of the factors, the product is always 0; otherwise, products that have an even number of negative factors are positive, whereas those that have an odd number of negative factors are negative.
Problem Find the product.
a. (600)(−40)(−1,000)(0)(−30)
b. (−3)(−10)(−5)(25)(−1)(−2)
c. (−2)(−4)(−10)(1)(−20)
Solution
a. (600)(−40)(−1,000)(0)(−30)

Step 1. 0 is one of the factors, so the product is 0.
(600)(−40)(−1,000)(0)(−30) = 0
b. (−3)(−10)(−5)(25)(−1)(−2)

Step 1. Find the product, ignoring the signs.
(3)(10)(5)(25)(1)(2) = 7,500
Step 2. You have five negative factors, so make the product negative.
(−3)(−10)(−5)(25)(−1)(−2) = −7,500
c. (−2)(−4)(−10)(1)(−20)

Step 1. Find the product, ignoring the signs.
(2)(4)(10)(1)(20) = 1,600
Step 2. You have four negative factors, so leave the product positive.
(−2)(−4)(−10)(1)(−20) = 1,600

Division of Signed Numbers
Rule 8. To divide two numbers, divide their absolute values (being careful to make sure you don’t divide by 0) and then follow the rules for multiplication of signed numbers.
Problem Find the quotient.
a. 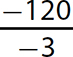
b. 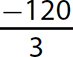
c. 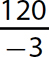
d. 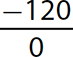
e. 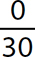
Solution
a. 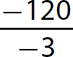

Step 1. Divide 120 by 3.
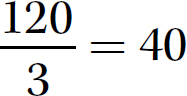
Step 2. The signs are the same (both negative), so keep the quotient positive.
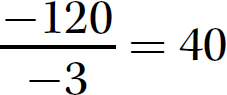
b. 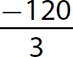

Step 1. Divide 120 by 3.
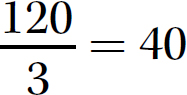
Step 2. The signs are opposites (one negative and one positive), so make the quotient negative.
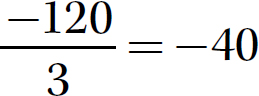
c. 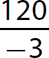

Step 1. Divide 120 by 3.
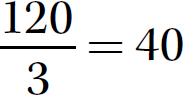
Step 2. The signs are opposites (one positive and one negative), so make the quotient negative.
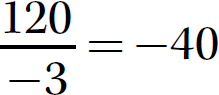
d. 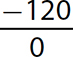

Step 1. The divisor (denominator) is 0, so the quotient is undefined.
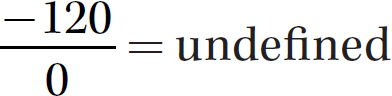
e. 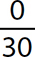

Step 1. The divisor is nonzero and the dividend (numerator) is 0, so the quotient is 0.
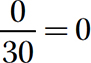
To be successful in algebra, you must memorize the rules for adding, subtracting, multiplying, and dividing signed numbers. Of course, when you do a computation, you don’t have to write out all the steps. For instance, you can mentally ignore the signs to obtain the absolute values, do the necessary computation or computations, and then make sure your result has the correct sign.
Exercise 2

For 1–3, simplify.
1. |−45|
2. |5.8|
For 4 and 5, state in words.
4. −9 + −(−4) = −9 + 4
5. −9 − (−4) = −9 + 4
For 6–20, compute as indicated.
6. −80 + −40
7. 0.7 + −1.4
10. (−100)(−8)
13. −450.95 − (−65.83)
16. −458 + 0
20. (−3)(1)(−1)(−5)(−2)(2)(−10)
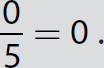 . But if 0 is the divisor, the quotient is undefined. Thus,
. But if 0 is the divisor, the quotient is undefined. Thus, 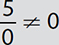 and
and 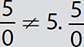 has no answer because division by 0 is undefined!
has no answer because division by 0 is undefined!