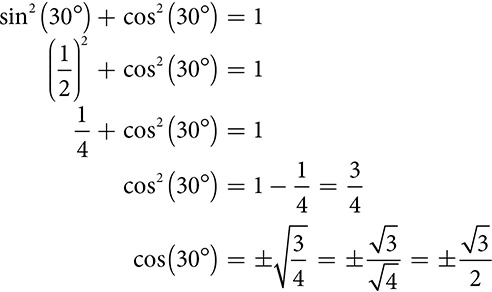CHAPTER 10
Right Triangle Trigonometry
Trigonometry means “triangle measurement.” It uses ideas from similarity to provide a means of finding measurements of sides or angles in right triangles.
Similar Right Triangles
To be certain that two triangles are similar, all that is necessary is to show that two angles in one triangle are congruent to two angles of the other. Because all right triangles have a right angle, they’re halfway to being similar. All that’s needed is to find a pair of acute angles, one from each triangle, that are congruent. That means that if you have a right triangle with a 23° angle, it’s similar to every other right triangle with a 23° angle. It’s as if the universe of right triangles is divided into families of similar right triangles, based on the size of the acute angles. In the figure below, ΔABK ~ ΔACJ ~ ΔADI ~ ΔAEH ~ ΔAFG. All of these triangles are similar because each has a right angle and each contains ∠A.

Let’s focus on ΔABK and ΔAFG, the smallest and largest of the group. Obviously ∠A ≅ ∠A, and the right angles ∠ABK and ∠AFG are congruent, so by the Third Angle theorem, ∠AKB ≅ ∠AGF. Corresponding sides are in proportion, and the proportion for these two triangles would say  . The last ratio in that proportion is the ratio of the two hypotenuses, and the middle ratio compares the sides opposite ∠A. Sides
. The last ratio in that proportion is the ratio of the two hypotenuses, and the middle ratio compares the sides opposite ∠A. Sides  and
and 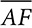 , whose lengths are compared in the first ratio, are the sides adjacent to ∠A. Of course, ∠A is between two sides, but one is always called the hypotenuse, so the non-hypotenuse side is referred to as the adjacent side. The proportion above says
, whose lengths are compared in the first ratio, are the sides adjacent to ∠A. Of course, ∠A is between two sides, but one is always called the hypotenuse, so the non-hypotenuse side is referred to as the adjacent side. The proportion above says 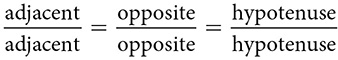 . Whatever scale factor enlarges or reduces the adjacent sides affects the other sides the same way.
. Whatever scale factor enlarges or reduces the adjacent sides affects the other sides the same way.
If we focus on just two of the ratios at a time, and apply properties of proportions, 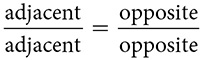 could become
could become 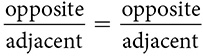 , and
, and  could become
could become 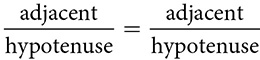 . For example,
. For example,  says the ratio of the adjacent side to the opposite side in little ΔABK is the same as the ratio of the adjacent side to the opposite in big ΔAFG.
says the ratio of the adjacent side to the opposite side in little ΔABK is the same as the ratio of the adjacent side to the opposite in big ΔAFG.
There are many different ways of organizing the information about corresponding sides into proportions. The key is to have a plan for what you want to compare, and hold to that for the entire proportion.
Basic Ratios
As the last few exercises suggest, a particular ratio of opposite side to hypotenuse, or adjacent side to opposite side, or whatever, turns out to be the same for every triangle in a particular family. If your right triangle has a 60° angle, the ratio of the side to adjacent to the 60° angle to the hypotenuse is 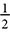 . It may be that the adjacent side is 3 inches and the hypotenuse is 6 inches, or it may be that the adjacent side is 20 miles and the hypotenuse is 40 miles. It will always reduce to
. It may be that the adjacent side is 3 inches and the hypotenuse is 6 inches, or it may be that the adjacent side is 20 miles and the hypotenuse is 40 miles. It will always reduce to 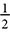 . Not every ratio will be such a tidy fraction. If your angle is 53° instead of 60°, the ratio will be an irrational number approximately equal to 0.545, but just as the ratio will be
. Not every ratio will be such a tidy fraction. If your angle is 53° instead of 60°, the ratio will be an irrational number approximately equal to 0.545, but just as the ratio will be 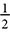 for the entire 60° family, it will be approximately 0.545 for the entire 53° family.
for the entire 60° family, it will be approximately 0.545 for the entire 53° family.
If every family of right triangles has a set value for each of the six possible ratios, then it makes sense to record those values to make them easier to use. First, we name the ratios to make them easier to talk about.

EXAMPLE
The values for all these ratios were recorded in tables, and you could look up the values you wanted to use (and you still can.) Now, scientific calculators or graphing calculators can provide the values for you. You’ll see keys for sin, cos, and tan on your calculator. If you want the value for the sine, cosine, or tangent for any family of right triangles, those keys will provide that information.
EXAMPLE
Finding a Side
Because you’re able to call up the value of a particular ratio for any family, you can find the length of an unknown side without needing to have two similar triangles. You just need to have one right triangle, know the measurement of one acute angle, and know the length of one side.
To use trig ratios to find a missing side in a right triangle:

Finding an Angle
Trig ratios give you a quick way to find an unknown side of a right triangle, as long as you know the measure of one acute angle of the right triangle. But what if you don’t know the measure of the angle? What if the measure of the angle is exactly what you’re trying to find?
You can do that with a little more information. You’ll need to know two sides of the right triangle, and you’ll need the inverse operation. You’ve met other inverses; square roots undo the work of squaring, for example. When you write cos(60) = 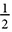 , you’re saying the right triangles in the 60° family have a ratio of adjacent side to hypotenuse that reduces to
, you’re saying the right triangles in the 60° family have a ratio of adjacent side to hypotenuse that reduces to  . What you need now is to say “what angle has a cosine value of
. What you need now is to say “what angle has a cosine value of  ?” You can write that as
?” You can write that as  . The −1 is not an exponent but a symbol for the inverse or opposite process. To find the angle that has a sine equal to
. The −1 is not an exponent but a symbol for the inverse or opposite process. To find the angle that has a sine equal to 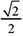 , you want
, you want 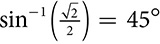 .
.
There is another notation for the inverse of the trig relationships that is sometimes used. Instead of 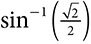 , the same idea could be expressed as
, the same idea could be expressed as 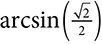 ,
, 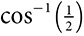 could be written as
could be written as 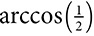 , and
, and  could be arctan(1).
could be arctan(1).
To find the measure of an acute angle of a right triangle:

EXAMPLE
Reciprocal and Complementary Relationships
When the trig ratios were named and defined, you may have noticed that there were two ratios that involved each pair of sides. The six different ratios are three pairs of reciprocals, and like all reciprocal pairs, their product is 1.

The reciprocals give you a choice when you’re trying to find an unknown side. If you know the opposite and are looking for the adjacent, you can use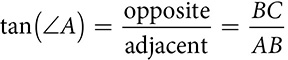 or
or 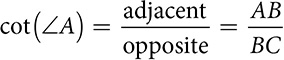 , whichever you prefer. Each has an advantage. If you are looking for AB, you may prefer to have the variable in the numerator, because it’s faster to solve. On the other hand, using sin, cos, or tan means you have a key on your calculator that will give you that value. You’ll have to work a bit to get the value of sec, csc, or cot.
, whichever you prefer. Each has an advantage. If you are looking for AB, you may prefer to have the variable in the numerator, because it’s faster to solve. On the other hand, using sin, cos, or tan means you have a key on your calculator that will give you that value. You’ll have to work a bit to get the value of sec, csc, or cot.
EXAMPLE
The “co” in the names of three of the six trig ratios comes from “complementary.” Two angles are complementary if their measures add to 90°, and the two acute angles in a right triangle are complementary. You may have noticed that the sine of one angle in a right triangle is the same value as the cosine of the other angle. The sine of one angle is the cosine of its complement. The complementary relationships are sine and cosine, secant and cosecant, and tangent and cotangent.

If you’re trying to find the measure of an acute angle in ΔABC, and you know the lengths of leg  and hypotenuse
and hypotenuse  , you can use
, you can use 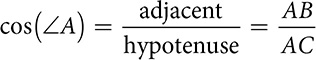 or
or 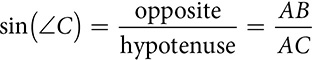 , depending on which angle you want to find. The cosine of ∠A is the sine of ∠C.
, depending on which angle you want to find. The cosine of ∠A is the sine of ∠C.
Pythagorean Identity
The famous rule known as the Pythagorean theorem says that if a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse, then  . All of the trig ratios involve the lengths of sides of right triangles, and the Pythagorean theorem provides some information about the relationships among the ratios. Consider right triangle ΔRST with right angle ∠S, and label legs
. All of the trig ratios involve the lengths of sides of right triangles, and the Pythagorean theorem provides some information about the relationships among the ratios. Consider right triangle ΔRST with right angle ∠S, and label legs  and
and  as a and b, and hypotenuse
as a and b, and hypotenuse  as c. Think about the trig ratios for ∠T.
as c. Think about the trig ratios for ∠T.
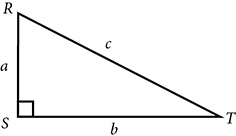

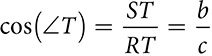
Square each ratio by squaring the numerator and squaring the denominator.

They have a common denominator, so look at what happens when they’re added.

The Pythagorean theorem says  .
.

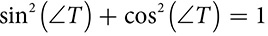
For any acute angle, the square of the sine of the angle plus the square of the cosine of the angle always equals one.
This observation, known as the Pythagorean identity, allows you to find the cosine of an angle if you know its sine, or find the sine if you know the cosine.
EXAMPLE
For now, only the positive square root will make sense in your work, but later the negative option will play a role.
While 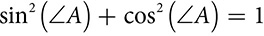 is what is usually thought of as the Pythagorean identity, it is actually one of three. Divide each term by
is what is usually thought of as the Pythagorean identity, it is actually one of three. Divide each term by  to get an identity involving cotangent and cosecant.
to get an identity involving cotangent and cosecant.
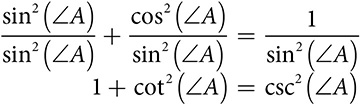
Or divide the original by  to get an identity involving tangent and secant.
to get an identity involving tangent and secant.

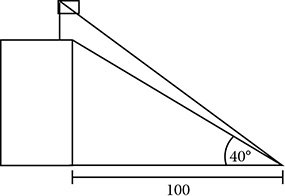
Modeling with Trigonometry
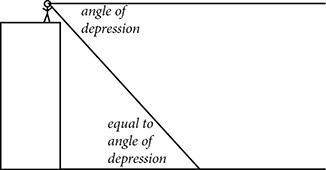
Right triangle trigonometry can often provide tools for modeling real-life situations and solving problems. When those situations are described, the description often includes “angle of elevation” or “angle of depression.” These angles provide important information but may or may not actually be in the right triangle.
EXAMPLE

 .
.
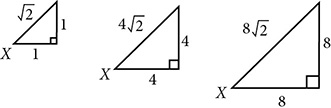
 Instead of “for every right triangle in the 60° family, the ratio of the adjacent side to the hypotenuse is
Instead of “for every right triangle in the 60° family, the ratio of the adjacent side to the hypotenuse is 
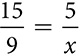 , then 15x = 45 and x = 3.
, then 15x = 45 and x = 3.
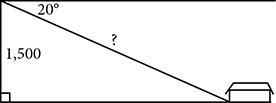
 and you can find out that tan(59°) is approximately 1.66. That takes the place of the ratio from ΔABC, and you can check that 15 ÷ 9 is very close to the value the calculator gives for tan(59°).
and you can find out that tan(59°) is approximately 1.66. That takes the place of the ratio from ΔABC, and you can check that 15 ÷ 9 is very close to the value the calculator gives for tan(59°).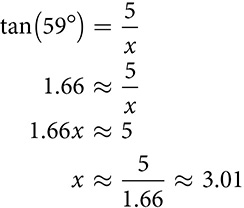
 , which measures 38 cm. If m∠X = 30°, find the length of leg
, which measures 38 cm. If m∠X = 30°, find the length of leg 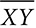 and the length of
and the length of  .
. .
. .
.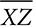 in rectangle WXYZ if m∠WXZ = 47° and XW = 5 meters?
in rectangle WXYZ if m∠WXZ = 47° and XW = 5 meters? measures 14 cm and leg
measures 14 cm and leg 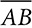 measures 8 cm. To find the measure of ∠C, notice that you have the hypotenuse and the side opposite ∠C. The opposite and hypotenuse can create the sine ratio.
measures 8 cm. To find the measure of ∠C, notice that you have the hypotenuse and the side opposite ∠C. The opposite and hypotenuse can create the sine ratio. 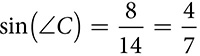 . Simplifying the fraction is not absolutely necessary, so use
. Simplifying the fraction is not absolutely necessary, so use  if you prefer. Write
if you prefer. Write  , and then find
, and then find 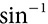 above the sin key on your calculator. Type 2nd and then sin to get
above the sin key on your calculator. Type 2nd and then sin to get  when rounded to the nearest thousandth.
when rounded to the nearest thousandth.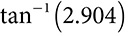
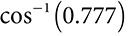
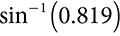

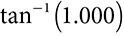
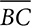 measures 62 cm. Find the measure of ∠A to the nearest tenth of a degree.
measures 62 cm. Find the measure of ∠A to the nearest tenth of a degree.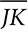 measures 14 inches, what is the measure of ∠L to the nearest tenth of a degree?
measures 14 inches, what is the measure of ∠L to the nearest tenth of a degree?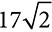 cm and a leg measures 17 cm.
cm and a leg measures 17 cm.
 , what is csc(∠A)?
, what is csc(∠A)? , what is cos(∠R)?
, what is cos(∠R)? and sin(60°) =
and sin(60°) =  , what is tan(60°)?
, what is tan(60°)?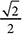 , what is cos(45°)?
, what is cos(45°)? , then:
, then: