CHAPTER 12
Circles
Much of the study of geometry is focused on polygons, figures built from line segments. The primary exception is the circle, a simple figure with so much to explore.
Circle Vocabulary
A circle is the set of all points in the plane at a fixed distance from a fixed point. The fixed point is called the center. The fixed distance is called the radius. The term radius is also used to refer to a line segment that connects the center to a point on the circle. A line segment that has its endpoints on the circle and passes through the center is the diameter.
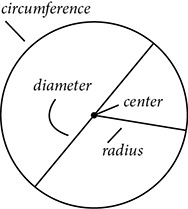
The distance around the circle is called the circumference, an idea similar to the perimeter of a polygon. The area of a circle is the area enclosed within it. The calculations of circumference and area rely on a constant, π, which is the ratio of the circumference to the diameter. The number π is usually approximated as 3.14 or 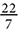 .
.
A portion of the circle, between two endpoints, is called an arc. Arcs are measured in degrees, with the full circle being 360°. Half a circle, called a semicircle, is an arc of 180°. An arc that is less than 180°, less than a semicircle, is a minor arc, and one that measures more than 180° but less than 360° is a major arc.
A circle is named by its center, as in “circle O,” but minor arcs are named by their endpoints, with an arc symbol above, as in  . To distinguish a major arc from a minor arc, major arcs are named with three letters, the two endpoints, and another point on the arc between the endpoints, as in
. To distinguish a major arc from a minor arc, major arcs are named with three letters, the two endpoints, and another point on the arc between the endpoints, as in 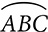 , which begins at A, passes through B, and ends at C.
, which begins at A, passes through B, and ends at C.

 Chords and Diameters In addition to the radius and diameter, there are a number of lines and line segments in and around circles. A line segment whose endpoints are points on the circle is a chord. The diameter is a chord that passes through the center of the circle; as such, it is the longest chord in the circle.
Chords and Diameters In addition to the radius and diameter, there are a number of lines and line segments in and around circles. A line segment whose endpoints are points on the circle is a chord. The diameter is a chord that passes through the center of the circle; as such, it is the longest chord in the circle.
 Secants and Tangents If a chord is extended beyond the circle, the resulting line is called a secant. A tangent is a line that touches the circle at only one point. Two circles may have a common tangent. If that tangent passes between the two circles, so that it crosses a line segment connecting the centers, it is an internal tangent. If it does not cross that line segment, it is externally tangent to the two circles.
Secants and Tangents If a chord is extended beyond the circle, the resulting line is called a secant. A tangent is a line that touches the circle at only one point. Two circles may have a common tangent. If that tangent passes between the two circles, so that it crosses a line segment connecting the centers, it is an internal tangent. If it does not cross that line segment, it is externally tangent to the two circles.

Circles may be tangent to one another, if they touch at just one point. If the two circles bump up against one another, they are externally tangent. If one circle is inside the other, just touching one point on the outer circle, the circles are internally tangent. If one circle sits inside another so that they have the same center and do not touch, they are called concentric circles.

Circumference and Area of Circles
The circumference of a circle is a measurement of the distance around the circle. Early mathematicians noticed that the ratio of the circumference of a circle to its diameter was always a little more than 3. Different cultures made different estimates of that number, but all a little more than 3.
Today we refer to that number as pi, using the symbol π. Mathematicians have calculated thousands of digits of the decimal of π, but it has no end, so if we want an exact value, we’ll just say π and if we want an approximate value, we’ll use one of the common approximations: 3.14 or  . Calculators generally have a key for π, which will give more decimal places, like 3.141592654, but that is still approximate.
. Calculators generally have a key for π, which will give more decimal places, like 3.141592654, but that is still approximate.
 Circumference C = πd = 2πr, where d is the diameter and r is the radius. You can use whichever version of the formula is convenient for the information you have and the value for which you’re looking.
Circumference C = πd = 2πr, where d is the diameter and r is the radius. You can use whichever version of the formula is convenient for the information you have and the value for which you’re looking.
 Area
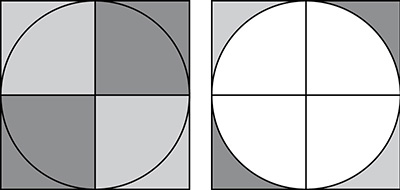
Area 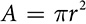 , where r is the radius. By overlaying a circle with four squares, each with sides the length of the radius, you can see that
, where r is the radius. By overlaying a circle with four squares, each with sides the length of the radius, you can see that  is larger than the area of the circle.
is larger than the area of the circle.
The actual formula can be derived by cutting the circle into sectors and rearranging them to create something that looks a lot like a parallelogram. The smaller you make the sectors, the more of them you have, and the more the rearrangement resembles a parallelogram. That near-parallelogram has a height equal to the radius, and a slightly bumpy base equal to half the circumference, or πr. The area of the rearranged circle is A = r(πr) or 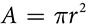 .
.

Angle Measurement
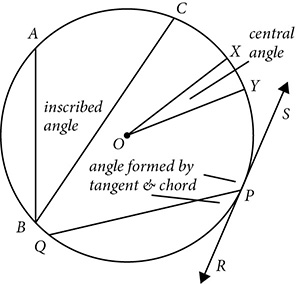
There are many different types of angles that can be drawn in and around circles, and it may seem as those each has its own rule for measurement, but in fact, they can all be organized under four rules, depending on where the vertex of the angle is.
 Vertex at the center measure of the angle = measure of the arc
Vertex at the center measure of the angle = measure of the arc
The central angle takes its name from the fact that its vertex is the center of the circle. Its sides are radii, and the number of degrees of arc between the points at which those radii touch the circle is the measure of both the arc and the central angle.
 Vertex on the circle measure of the angle =
Vertex on the circle measure of the angle = 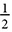 measure of the arc
measure of the arc
An inscribed angle is formed by two chords that meet at a point on the circle. The measure of the angle is half the measure of the arc intercepted by those chords.
An angle formed by a tangent and a chord has its vertex on the circle, at the point of tangency. The tangent and chord actually form a linear pair, and each angle is half the measure of the arc on that side of the chord.
EXAMPLE
 Vertex inside the circle measure of the angle =
Vertex inside the circle measure of the angle =  sum of the two arcs
sum of the two arcs
When two chords intersect within the circle, their endpoints divide the circle into four arcs, and the chords create two pairs of vertical angles. The measure of the angle is the average of the arcs it and its vertical angle partner intercept.
EXAMPLE
 Vertex outside the circle measure of the angle =
Vertex outside the circle measure of the angle =  difference of the two arcs
difference of the two arcs
 Angle formed by two tangents from the same point The tangents each touch the circle at one point. These two points of tangency divide the circle into two arcs: a smaller one near the vertex of the angle, and a larger one that is the remainder of the circle. If the smaller arc is x°, the larger one is 360° − x°, and the measure of the angle is
Angle formed by two tangents from the same point The tangents each touch the circle at one point. These two points of tangency divide the circle into two arcs: a smaller one near the vertex of the angle, and a larger one that is the remainder of the circle. If the smaller arc is x°, the larger one is 360° − x°, and the measure of the angle is 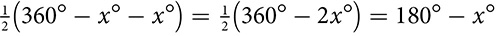
 Angle formed by a tangent and a secant from the same point The tangent touches the circle at one point and the secant cuts through two points. The smaller arc is from the point of tangency to the first time the secant intersects the circle. The larger arc is from the second intersection with the secant to the point of tangency. The measure of the angle is
Angle formed by a tangent and a secant from the same point The tangent touches the circle at one point and the secant cuts through two points. The smaller arc is from the point of tangency to the first time the secant intersects the circle. The larger arc is from the second intersection with the secant to the point of tangency. The measure of the angle is 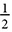 (measure of larger arc – measure of smaller arc).
(measure of larger arc – measure of smaller arc).
 Angle formed by two secants from the same point Each secant intersects the circle in two points. The smaller arc is the arc between the first intersection of each secant with the circle. The larger arc is the portion of the circle between the second intersections. The measure of the angle is
Angle formed by two secants from the same point Each secant intersects the circle in two points. The smaller arc is the arc between the first intersection of each secant with the circle. The larger arc is the portion of the circle between the second intersections. The measure of the angle is 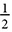 (measure of larger arc – measure of smaller arc).
(measure of larger arc – measure of smaller arc).
EXAMPLE
Segments in Circles
There are several different relationships among segments in and around circles, which aren’t quite as easy to categorize. There are the segments that simply are congruent.
 In any circle, all radii are congruent, all diameters are congruent, and the length of a diameter is twice the length of a radius.
In any circle, all radii are congruent, all diameters are congruent, and the length of a diameter is twice the length of a radius.
 If two tangent segments are drawn to a circle from the same point, the tangent segments are congruent.
If two tangent segments are drawn to a circle from the same point, the tangent segments are congruent.
The next two are a little more complicated.
 The length of a chord is inversely related to its distance from the center. The closer to the center the chord is drawn, the longer it will be. The longest chord is the diameter.
The length of a chord is inversely related to its distance from the center. The closer to the center the chord is drawn, the longer it will be. The longest chord is the diameter.
 A diameter or radius perpendicular to a chord bisects the chord and its arc.
A diameter or radius perpendicular to a chord bisects the chord and its arc.
Draw radii from the center to the endpoints of the chord, and you can prove the right triangles congruent. The two sections of the chord will be congruent by CPCTC. The arcs will be congruent because their central angles are congruent.

The next group usually expresses the relationship in terms of products, but those products come from cross-multiplying proportions because the relationships are based on similar triangles.
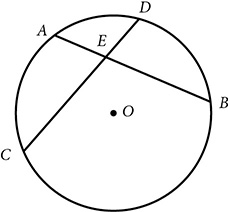
 When two chords intersect in a circle, the product of the lengths of the segments of one chord is equal to the products of the lengths of the segments of the other.
When two chords intersect in a circle, the product of the lengths of the segments of one chord is equal to the products of the lengths of the segments of the other.

ΔEAC ~ ΔEDB, so 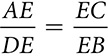 and AE ⋅ EB = DE ⋅ EC
and AE ⋅ EB = DE ⋅ EC
 If two secant segments are drawn to a circle from the same point, the product of the lengths of the external segment and the whole secant is the same for both secants.
If two secant segments are drawn to a circle from the same point, the product of the lengths of the external segment and the whole secant is the same for both secants.

ΔPTQ ~ ΔPRS, so 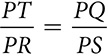 and PS ⋅ PT = PQ ⋅ PR
and PS ⋅ PT = PQ ⋅ PR
 If a secant and a tangent are drawn to a circle from the same point, the product of the lengths of the external segment and the whole secant is equal to the length of the tangent segment squared.
If a secant and a tangent are drawn to a circle from the same point, the product of the lengths of the external segment and the whole secant is equal to the length of the tangent segment squared.
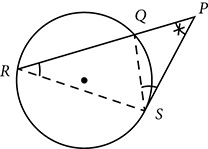
ΔPRS ~ ΔPSQ, so 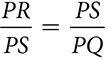 and PQ ⋅ PR = PS2
and PQ ⋅ PR = PS2
Inscribed and Circumscribed Polygons and Constructing Tangents
When you constructed a regular polygon in a circle, you inscribed the polygon in the circle. You constructed it in such a way that the vertices were points on the circle. Each interior angle of the polygon was an inscribed angle of the circle. Each side of the polygon was a chord. The polygon is inside the circle, and as large as it can be without breaking out of the circle.
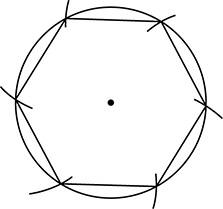
If, on the other hand, a polygon is circumscribed about a circle, each of its sides is tangent to the circle. The interior angles of the polygon are angles formed by two tangents. The circle is within the polygon, as large as it can be without breaking through the sides of the polygon.

Inscribing a polygon in a circle usually involves constructions that divide the circle into arcs of equal measure and then connecting some or all of the points that define the arcs with chords. Circumscribing a polygon about a circle will require the construction of tangent lines. There are two constructions that produce tangent lines, depending on whether you are given the point of tangency or a point outside the circle.
The construction of a tangent to a point on the circle relies on the fact that a radius or diameter drawn to the point of tangency is perpendicular to the tangent. If you are given the point of tangency, you can construct a tangent by extending the radius through the point of tangency and then constructing a perpendicular to the radius at the given point.
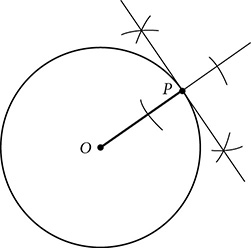
Constructing a tangent to the circle from a point outside the circle is not as simple, however, because you do not know where the point of tangency should be. This construction will still rely on the radii perpendicular to the tangent, but finding the right radius to the right point of tangency will take a little more work. Start by connecting the center of the circle to the point from which the tangent will be drawn. This line is going to become the diameter of a new circle and the hypotenuse of a right triangle inscribed in that circle. The legs of that right triangle will be the radius of the original circle and the tangent we want. To make that happen, we have to make sure the vertex of the right angle is a point on both the new circle and the original circle:
EXAMPLE
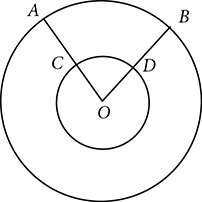
Arc Measure, Arc Length, and Area of a Sector
Arc measure and arc length are related but should not be confused. The measure of an arc is a number of degrees equal to the measure of the central angle that intercepts that arc. Because it measures an amount of rotation, it is the same in small circles as in large circles. The radius has no effect.
The measure of an arc is equal to the measure of the central angle that intercepts it. Arc measure is given in degrees.
But the size of the radius does make a difference in arc length. The length of an arc is a fraction of the circumference and depends on both the amount of rotation and the radius. An arc of a certain measure has a greater length in a large circle than in a small one.
Arc length is a fraction of the circumference and is measured in units of length like centimeters or inches. The common symbol for arc length is s.
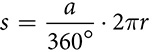
where s is the arc length, r is the radius, and a is the measure of the arc or its central angle.
EXAMPLE
Just as arc length is a fraction of the circumference of a circle, the area of a sector is a fraction of the area of the circle. Both depend upon the measure of the central angle or the intercepted arc.

where a is the measure of the central angle or its arc and r is the radius.
EXAMPLE
Radian Measure
Angles are commonly measured in degrees. A degree is a unit of measure based on dividing a full rotation into 360 parts. Each part is 1 degree. Working in circles and carrying the idea of trig ratios into the algebraic world of functions leads to a different system of measurement of rotation and therefore of angles. Radian measure is built on a unit of one radian.
 1 radian The measure of an angle whose intercepted arc has a length equal to the radius
1 radian The measure of an angle whose intercepted arc has a length equal to the radius

The definition of the radian is rooted in the circle. It uses the radius as a way to divide the rotation. The circumference of a circle is C = 2πr, so if it is divided into arcs equal to the radius, there will be 2π, or slightly more than 6 arcs in the circumference. Each arc is the intercepted arc of an angle of 1 radian, which means that there are 2π radians in a full rotation.
The ratio of 1 unit to the whole rotation can be used to convert between radians and degrees.
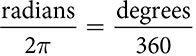
EXAMPLE
Using radian measure makes it easier to move from trigonometry in triangles to trigonometric functions, but it also makes arc length and area of sectors easier. Remember that both of those involve a fraction which was the number of degrees in the arc or central angle over 360 in the full rotation. If we use the symbol θ for the radian measure of the central angle and 2π for the full rotation, those formulas become simpler.
Arc length 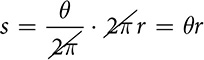
Area of sector 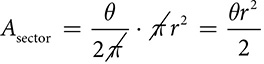

 .
. .
. .
. .
. and m∠QPS =
and m∠QPS =  .
.
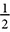 (m
(m + m
+ m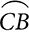 ) and m∠AEC = m∠DEB =
) and m∠AEC = m∠DEB = 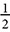 (m
(m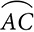 + m
+ m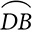 )
)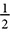 (m
(m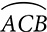 − m
− m (m
(m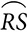 − m
− m )
)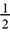 (m
(m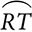 − m
− m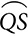 )
)
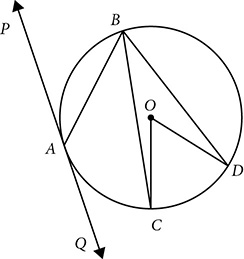
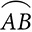 measures 50°, what is the measure of ∠PAB?
measures 50°, what is the measure of ∠PAB? ?
? ?
? were drawn, what would be the measure of ∠BAD?
were drawn, what would be the measure of ∠BAD?
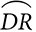 = 30°,
= 30°, 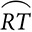 = 90°,
= 90°,  = 75°,
= 75°,  = 15°.
= 15°.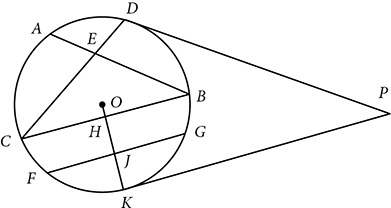
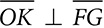 . If FG = 12 and OK = 10, how long is
. If FG = 12 and OK = 10, how long is 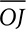 ?
? .
.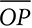 is drawn, find the length of
is drawn, find the length of 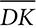 were drawn, what conclusion could you draw about ∠PDK and ∠PKD?
were drawn, what conclusion could you draw about ∠PDK and ∠PKD?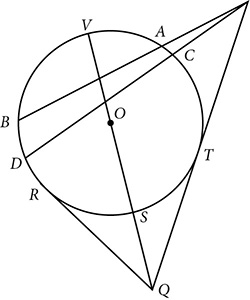
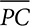 ?
?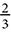 , find PT.
, find PT. intersects
intersects 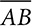 , the segments of
, the segments of 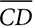 , the segments of
, the segments of 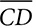 can be represented as x +1 and x + 2, and their product is 72. Find the lengths of
can be represented as x +1 and x + 2, and their product is 72. Find the lengths of  .
. . Call the midpoint M. M will be the center of the new circle.
. Call the midpoint M. M will be the center of the new circle. , scribe a circle. Circle M should pass through P and O, and intersect the circle in two points. Those two points, which we’ll label Q and R, are the points of tangency.
, scribe a circle. Circle M should pass through P and O, and intersect the circle in two points. Those two points, which we’ll label Q and R, are the points of tangency.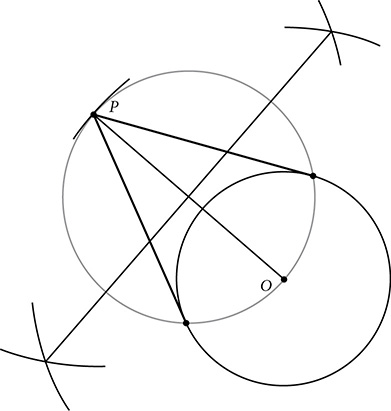



 and
and 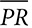 .
.
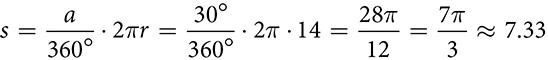 cm
cm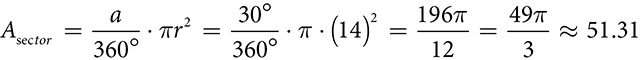 cm2
cm2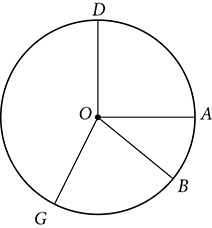
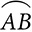 ? How long is
? How long is  ?
?
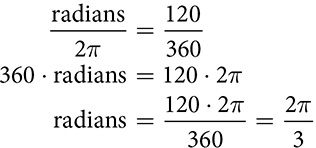
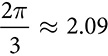 radians.
radians.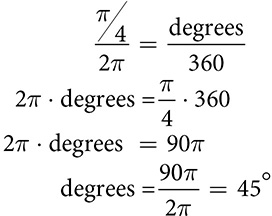
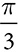 radians
radians radians if the radius of the circle is 24 inches.
radians if the radius of the circle is 24 inches.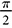 radians if the diameter of the circle is 10 meters.
radians if the diameter of the circle is 10 meters.