CHAPTER 14
Three-Dimensional Figures
Much of the geometry studied in school is plane geometry, focused on points, lines, and two-dimensional figures like polygons and circles. The world we live in is not two-dimensional, of course, and so it makes sense to spend some time looking at three-dimensional objects. Commonly referred to by the generic term solids, they are not actually filled, but these three-dimensional objects can be used for modeling real situations.
Polyhedrons
A polyhedron is a three-dimensional object formed by joining polygons at their edges. A polyhedron has faces, which are polygons, or sections of a plane. It has edges, which are the line segments where two faces meet, and vertices, or points where several faces come together. Convex polyhedrons, like convex polygons, have no dents or holes. Polyhedrons are named by the number of faces, similar to the way polygons are named by the number of sides. A polygon with five sides is a pentagon; a polyhedron with five faces is a pentahedron. This general naming system is often replaced by more common names. A regular hexahedron is more likely to be called a cube.
In the 18th century, Swiss mathematician Leonhard Euler developed a formula to relate the number of faces, number of edges, and number of vertices in any convex polyhedron. With a bit of observation, you may see it too. Think about a cube.

How many faces? How many edges? How many vertices?
Now look at a square pyramid.

How many faces? How many edges? How many vertices?
Can you see it yet? Look at other polyhedrons. Count faces, edges, and vertices. Add the number of faces to the number of vertices. Notice anything?
Euler’s Polyhedron Formula Faces + Vertices = Edges + 2
You’ll see the formula rearranged in different ways, like Faces + Vertices – Edges = 2, but choose the one that’s easiest for you to remember.
There are other three-dimensional figures that do not meet the definition of polyhedron, usually because one or more of their surfaces are not polygons. Think of a sphere or a cone or a cylinder. These shapes that curve don’t qualify as polyhedrons, but many ideas used in dealing with polyhedrons can be applied, with a little modification, to some of their curved cousins.
Surface Areas of Prisms and Cylinders
Surface area is just the total of the area of all the faces of a polyhedron. If you’re looking at a cube, you see 6 faces, each of them a square with the same side length. You find the area of one of the squares, by squaring the length of its side, and multiply by 6.
As the polyhedrons become more complicated, of course, it’s not always that easy. How many faces? What shape? Are they all the same shape? Do you have the dimensions you need to plunge right into finding areas? That’s why many people like to take the time to decompose a polyhedron into a flat image, called a net, which can fold up into the polyhedron. A net allows you to see each of the polygons that form the polyhedron and calculate area piece by piece.
A net for a cube might look like this:
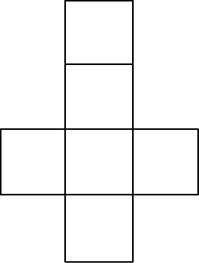
A net for a square pyramid might look like this:
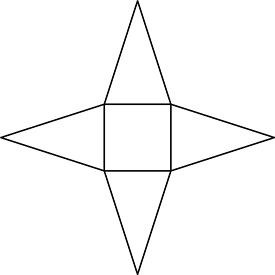
A prism is a polyhedron with two identical, parallel bases, surrounded by lateral sides that are parallelograms. If the bases are directly above one another and the lateral sides are rectangles, the prism is a right prism. The prism takes its name from the shape of the bases. If the bases are pentagons, the prism is a pentagonal prism. A triangular prism has bases that are triangles.
If the bases of a prism are regular polygons, the lateral area can be found by finding the area of one parallelogram and multiplying by the number of sides, but if the bases are not regular, the area of each parallelogram may need to be calculated separately. In that case, a well-labeled net is helpful.
EXAMPLE
Cylinders are all around, as cans or other containers, or the shape of everything from poles to pencils. A cylinder is not a polyhedron because of its curved lateral surface, but breaking it down into a net shows how the surface area can still be found. The bases are both circles, so the area of the bases is 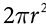 . The lateral area can be imagined as unrolling the label on a cylindrical can. It unwraps to a rectangle, with one dimension equal to the height of the cylinder and the other dimension equal to the circumference of the circle. The surface area of a cylinder is
. The lateral area can be imagined as unrolling the label on a cylindrical can. It unwraps to a rectangle, with one dimension equal to the height of the cylinder and the other dimension equal to the circumference of the circle. The surface area of a cylinder is 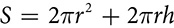 .
.
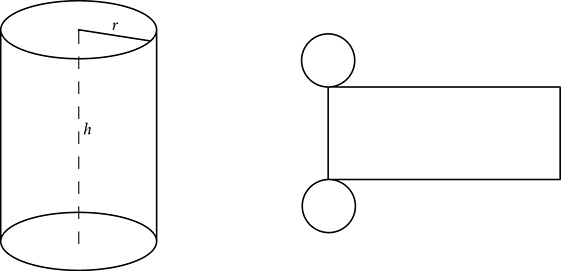
EXAMPLE
Volumes of Prisms and Cylinders
Imagine that you’ve been giving the task of packing children’s alphabet blocks into a box. You could just dump them in and hope for the best, but the blocks are cubes, 1 inch on each edge, so they will pack in nicely. If you have the patience to pack them, the blocks will settle into a layer, and the number of blocks in the layer will depend on the length and width of the box. In a box that measures 12 inches long, 8 inches wide, and 10 inches high, the bottom layer will have 8 rows of 12 blocks, or 96 blocks per layer, and you’ll be able to make 10 such layers, for a total of 960 blocks. The volume of the box is 960 cubic inches.
For a rectangular prism, the area of the base is length times width, so V = lwh, but for other prisms, finding volume will not always be as easy as length times width times height. The calculation of the base area will be more complicated, but volume is the area of the base times the height. The volume of a prism is  .
.
EXAMPLE
The idea of volume as area of the base times the height can be applied to cylinders with a small adjustment. The base of a cylinder is a circle, so the area of the base is 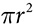 , and the volume of the cylinder is V = πr2h.
, and the volume of the cylinder is V = πr2h.
EXAMPLE
Surface Areas of Pyramids and Cones
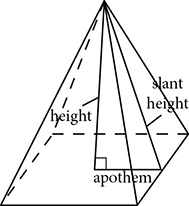
A pyramid is a polyhedron with one polygonal base and lateral sides that are triangles which tip in so that their vertices all meet at a point.

The net for a pyramid shows the base surrounded by triangles. The surface area of the pyramid is equal to the area of the base, B, plus the total of the areas of all the triangles. The area of each triangle is 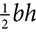 , but look carefully at the pyramid before you start to calculate. The base of each triangle is an edge of the base polygon, but the height of the triangle is not the height of the pyramid. The height of the pyramid is measured from the top point of the pyramid perpendicular to the base. The height of the triangle, which is called the slant height and designated as l, is the hypotenuse of a right triangle formed by the apothem of the base, the height of the pyramid, and the slant height. The apothem is the measure from the center of the base, perpendicular to an edge.
, but look carefully at the pyramid before you start to calculate. The base of each triangle is an edge of the base polygon, but the height of the triangle is not the height of the pyramid. The height of the pyramid is measured from the top point of the pyramid perpendicular to the base. The height of the triangle, which is called the slant height and designated as l, is the hypotenuse of a right triangle formed by the apothem of the base, the height of the pyramid, and the slant height. The apothem is the measure from the center of the base, perpendicular to an edge.
The slant height is 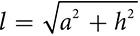 .
.
If B is the area of the base, l is the slant height, and P is the perimeter of the base, the surface area of a pyramid is 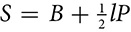 .
.
EXAMPLE
Applying similar thinking to a cone, you can see that the slant height is the hypotenuse of a right triangle formed by the radius of the base, the height of the cone, and the slant height: 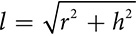 .
.
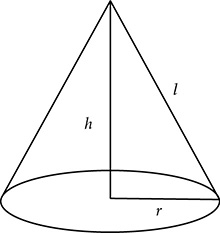
The area of the base of the cone is easy:  . Finding the lateral area of the cone is not as simple. If you unroll it for a net, you see that it is part, but not all, of a circle. But what part? And what is the radius of that circle? If you look at the process of unrolling the lateral area, you’ll see that the radius of this partial circle is actually the slant height, l. Realize too that when you roll this partial circle into a cone, it fits right around the circumference of the base. That means that the arc length of this partial circle is the circumference of the base, so s = 2πr.
. Finding the lateral area of the cone is not as simple. If you unroll it for a net, you see that it is part, but not all, of a circle. But what part? And what is the radius of that circle? If you look at the process of unrolling the lateral area, you’ll see that the radius of this partial circle is actually the slant height, l. Realize too that when you roll this partial circle into a cone, it fits right around the circumference of the base. That means that the arc length of this partial circle is the circumference of the base, so s = 2πr.
If it were a full circle, its circumference would be C = 2πl. The portion of the circle that forms the lateral area has an arc length that is 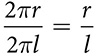 of the full circumference, so it will have
of the full circumference, so it will have  of the full area:
of the full area: 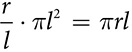 . To get the total surface area, add the base area and the lateral area:
. To get the total surface area, add the base area and the lateral area:  . The surface area of a cone is
. The surface area of a cone is 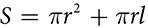 .
.
EXAMPLE
Volumes of Pyramids and Cones
Finding volumes of pyramids and cones is very similar to finding volumes of prisms and cylinders, but it is necessary to account for the fact that pyramids and cones narrow to a point and therefore will have a smaller volume. Fortunately, the adjustment is always the same. The volume of the pyramid is one-third the volume of the prism with the same base area and height, and the volume of a cone is one-third the volume of the cylinder with the same base and height.
 Volume of a pyramid
Volume of a pyramid 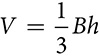
EXAMPLE
 Volume of a cone
Volume of a cone 
EXAMPLE
Spheres
Spheres get a category of their own. Their ball shape has no bases and no points, no flat faces. Deriving the formulas for the surface area and volume of a sphere requires calculus, so we won’t do that here, but there are some ways you can see the logic of them. Carefully peel an orange. Try to keep the peel in as few pieces as possible, and then flatten them on a surface. Break the orange into two halves. The cross section is a circle with area  for whatever the radius of the orange is. Place the two halves, circle side down, on the flattened peel and you should see they take up about half the space of the peel. You could fit two more of those circles. The surface area of a sphere with radius r is
for whatever the radius of the orange is. Place the two halves, circle side down, on the flattened peel and you should see they take up about half the space of the peel. You could fit two more of those circles. The surface area of a sphere with radius r is  .
.
EXAMPLE
If you wanted to create a container in which to place your orange, it would have to be at least as wide as the diameter of your orange, and at least as tall as that diameter. If you create a cylinder with the diameter of the orange, or 2r, and a height of 2r, the volume of that cylinder is 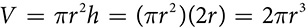 . Your whole orange would fit inside, but there would be space left over. The cylindrical container has a volume a bit more, but not a lot more, than the volume of the orange. The volume of a sphere with radius r is
. Your whole orange would fit inside, but there would be space left over. The cylindrical container has a volume a bit more, but not a lot more, than the volume of the orange. The volume of a sphere with radius r is  .
.
EXAMPLE
Modeling with Three-Dimensional Figures
Three-dimensional figures can be used to model real-life situations because real-life situations involve three-dimensional objects. Those objects may not be perfect cylinders or precisely a hexagonal pyramid, but they may be close enough to allow reasonable estimates.
One of the ways to estimate volumes of irregularly shaped objects is to think about cross sections. If you have one slice from a loaf of bread, you can measure its length, width, and thickness to find the volume of that slice. Then if the slices are all the same shape and size, you can find the volume of the loaf by multiplying the volume of one slice by the number of slices. If the slices are not all the same, you might divide the loaf into sections, with similar slices throughout each section.
Many common polyhedrons can be created by rotating common polygons. Rotate:
 A rectangle about one of its sides and you produce a cylinder.
A rectangle about one of its sides and you produce a cylinder.
 A right triangle about one of its legs and you produce a cone.
A right triangle about one of its legs and you produce a cone.
 A circle about one of its diameters and you produce a sphere.
A circle about one of its diameters and you produce a sphere.
Here too, you may want to break an object into parts. The body of a rocket might be modeled by placing a right triangle atop a rectangle and rotating the combination about a side.
Density
Earlier in this chapter, we noted that the general term of solid for three-dimensional figures could be misleading, because they could, in many cases, be hollow. But when they are in fact solid, it is possible to talk about the density of the polyhedron. Density is a comparison of an object’s mass to its volume. The density of water is 1 gram per cubic centimeter, while the density of honey is 1.33 grams per cubic centimeter, and the density of vegetable oil is a bit less than the density of water, at 0.92 g/cm3. The materials from which you might construct containers also have different densities. The density of aluminum is about 2.7 grams per cubic centimeter, while steel has a density of 8.05 g/cm3 and flexible PVC plastic is about 1.29 g/cm3.

Remember that mass, the actual amount of matter, is different from weight, although they are often spoken of as though they were the same. Weight depends on the force of gravity acting on the mass. If you travel into space, you may experience weightlessness. If you land on the moon, you will weigh less than you weigh on Earth, but your mass is always the same.
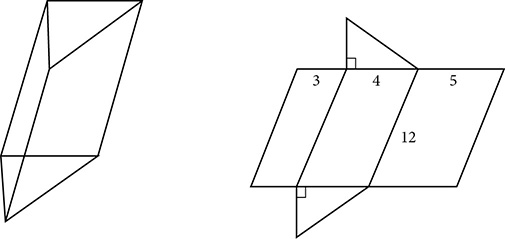
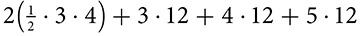 . Before evaluating that expression, stop to notice a possible shortcut. If the height of 12 is factored out of the last three terms, the result is the height of the prism times the perimeter of the base.
. Before evaluating that expression, stop to notice a possible shortcut. If the height of 12 is factored out of the last three terms, the result is the height of the prism times the perimeter of the base.
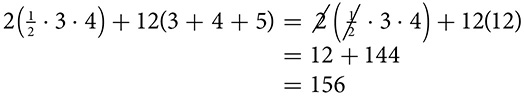
 becomes
becomes 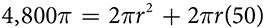 , which simplifies to
, which simplifies to 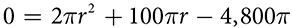 or
or  . Factor to get (r + 80)(r – 30) = 0, which produces two solutions. The negative solution, r = −80, is rejected, so the radius is 30 cm.
. Factor to get (r + 80)(r – 30) = 0, which produces two solutions. The negative solution, r = −80, is rejected, so the radius is 30 cm.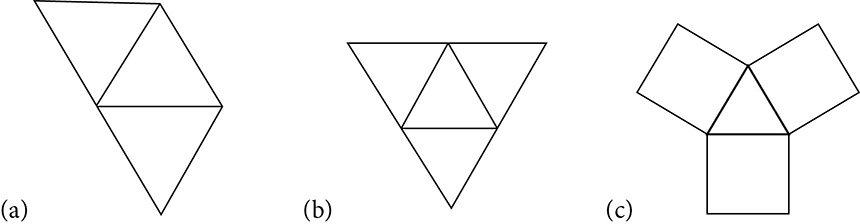
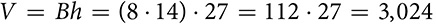 cubic inches.
cubic inches.
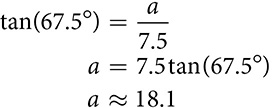
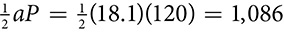 . Finally, you can calculate
. Finally, you can calculate 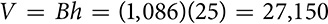 cubic centimeters.
cubic centimeters.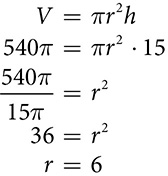
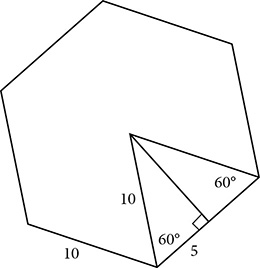
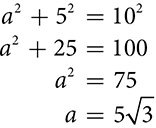
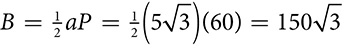

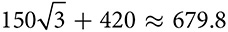
 inches. Its surface area is
inches. Its surface area is 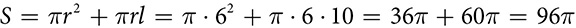 square inches.
square inches.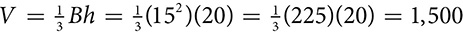 cubic centimeters.
cubic centimeters.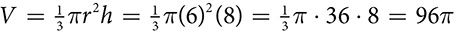 cubic inches.
cubic inches. square inches.
square inches.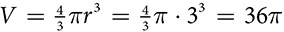 cubic inches.
cubic inches.