CHAPTER 9
Similarity
As mentioned in Chapter 7, the idea of congruence, the correspondence between two polygons of exactly the same size and shape, is one of the key relationships in geometry. The other is similarity, which finds correspondence between figures that are the same shape but different sizes. When a rigid transformation is applied to a polygon, it produces an image that is congruent to the pre-image. An image similar to the pre-image is created by applying a transformation called a dilation.
Dilations
A dilation is a transformation that produces an image which is the same shape as the pre-image, but a different size. If the image is larger than the pre-image, the dilation is an enlargement; if the image is smaller, the dilation is a reduction.
One way to visualize a dilation is to imagine a projector directing beams of light toward an image. The greater the distance between the projector and the surface on which the image falls, the larger the image will appear. The dilation is described by its center, a fixed point akin to the location of the projector, and by the scale factor, the ratio of image size to pre-image size. Enlargements have scale factors greater than 1, while reductions have scale factors less than 1. A scale factor of 3 indicates that the image is three times the size of the pre-image. A scale factor of ½ means the image is half the size of the pre-image.
Think of the center as the projector’s light source, sending beams of light toward the pre-image. It can be a point on the polygon or elsewhere in the plane. Focus your attention on the vertices of the polygon, which determine its shape. The beams of light that strike those vertices diverge as they continue on. A scale factor of 2 means that PA′ = 2 ⋅ PA. A scale factor less than 1 means the image is closer to the center, and therefore smaller.
EXAMPLE
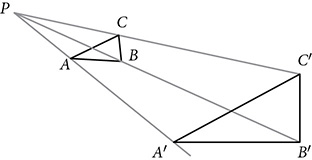
Like rigid transformations, dilations are often easier to draw if you work on a coordinate plane. In the figure below, ΔPQR is subjected to a dilation with a scale factor of 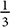 , centered at the origin. The distance from the origin to a point on the image, like R′, is
, centered at the origin. The distance from the origin to a point on the image, like R′, is 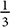 of the distance from the origin to the corresponding point R on the pre-image, but notice that in the image, the coordinates of each vertex of the image are
of the distance from the origin to the corresponding point R on the pre-image, but notice that in the image, the coordinates of each vertex of the image are 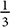 of the coordinates in the pre-image.
of the coordinates in the pre-image.
To perform a dilation centered at the origin, multiply the coordinates of the pre-image by the scale factor.
EXAMPLE
If the center of the dilation is not the origin, you can translate the center to the origin, apply the same translation to the pre-image, multiply by the scale factor, draw the image, and, finally, translate everything back.
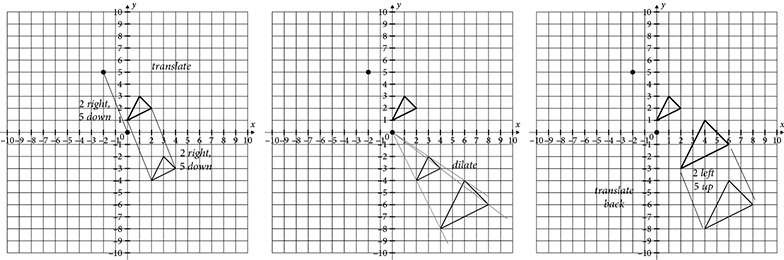
Similarity
Two polygons are similar if they are the same shape but different sizes, or put another way, if one is the image of another under a dilation. In order to accomplish this, the corresponding angles, which control the shape, must be congruent, and the corresponding sides must be enlarged or reduced by the same factor. In similar figures, corresponding angles are congruent and corresponding sides are in proportion.
The symbol for “is similar to” is ~, part of the symbol for “is congruent to,” ≅. Similar figures are the same shape (~) but not the same size (=). The way in which the similarity statement is written makes the correspondence clear, just as congruence statements spelled out the correspondence. If ΔABC ~ ΔYXZ, then ∠A ≅ ∠Y, ∠B ≅ ∠X, and ∠C ≅ ∠Z. The lengths of corresponding sides create the proportion  .
.
Proving Triangles Similar
Just as it is not necessary to prove all pairs of corresponding parts congruent in order to claim two triangles are congruent, it is not necessary to prove all corresponding angles congruent and all corresponding sides in proportion in order to show two triangles are similar. The most common method of showing two triangles are similar is “angle-angle.”
 AA If two angles of one triangle are congruent to the corresponding angles of the other triangle, then the triangles are similar.
AA If two angles of one triangle are congruent to the corresponding angles of the other triangle, then the triangles are similar.
It is not necessary to prove that the third pair of angles are congruent, because the Triangle Sum theorem guarantees that the sum of the three angles in any triangle is 180°, and so it takes little more than arithmetic to prove the Third Angle theorem: If two angles of one triangle are congruent to the corresponding angles of another triangle, then the third angles will also be congruent.
Other less commonly used shortcuts for showing two triangles similar involve showing some or all sides are in proportion.
 SSS If all three pairs of corresponding sides in one triangle are in proportion to the corresponding sides of another triangle, the triangles are similar.
SSS If all three pairs of corresponding sides in one triangle are in proportion to the corresponding sides of another triangle, the triangles are similar.
 SAS If two sides of one triangle are proportional to the corresponding sides of the other triangle and the angles included between those sides are congruent, then the triangles are similar.
SAS If two sides of one triangle are proportional to the corresponding sides of the other triangle and the angles included between those sides are congruent, then the triangles are similar.
After proving a pair of triangles congruent, you often needed to use the fact that corresponding parts of congruent triangles are congruent (CPCTC) to prove that a pair of angles or a pair of sides, not previously mentioned, was congruent. When you prove triangles similar, you may need to make an additional claim as well. It is not usually a claim about angles, but rather one about sides being in proportion. The reason you can claim that the proportion is true is “corresponding sides of similar triangles are in proportion,” but that doesn’t usually get a handy abbreviation.
Using Proportions
Knowing that corresponding sides of similar triangles are proportional can be helpful in finding missing dimensions. If you can write a proportion about the sides of similar triangles that contains enough known information, you can solve for the missing side(s).
There are a few key things about proportions worth reviewing. A proportion is a statement that says two ratios are equal. A proportion is usually written with the ratios as fractions, as in 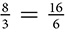 , but could be written on a single line like this: 8:3 = 16:6. The first and last numbers are called the extremes, and the two in the middle are called the means. The most important property of proportions is the Means-Extremes property, which says that the product of the means is equal to the product of the extremes.
, but could be written on a single line like this: 8:3 = 16:6. The first and last numbers are called the extremes, and the two in the middle are called the means. The most important property of proportions is the Means-Extremes property, which says that the product of the means is equal to the product of the extremes.
EXAMPLE
When the proportion involves a variable, cross-multiplying leads to an equation that can be solved.
EXAMPLE
Before we look at other properties of proportions, remember that the denominator of a fraction can never be zero. That won’t often come up when you’re working with lengths of sides, but be thoughtful when using variables.
 If
If 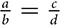 , then
, then 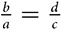 . You can invert the ratios. Remember to invert both.
. You can invert the ratios. Remember to invert both.
 If
If 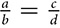 , then
, then 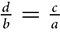 . You can swap the extremes. You can also swap the means.
. You can swap the extremes. You can also swap the means.
 If
If 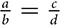 , then
, then 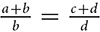 and
and 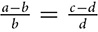 .
.  can be simplified to
can be simplified to  or
or 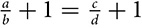 .
.
These are just telling you what things look like when you add (or subtract) an equal amount to both sides of the equation.
Dividing the Sides of a Triangle
A midsegment of a triangle is a line segment that connects the midpoints of two sides of a triangle. The Midsegment theorem says that the segment that connects the midpoints of two sides of a triangle is parallel to the third side and half as long.
 Midsegment theorem The segment that connects the midpoints of two sides of a triangle is parallel to the third side and half as long.
Midsegment theorem The segment that connects the midpoints of two sides of a triangle is parallel to the third side and half as long.
EXAMPLE
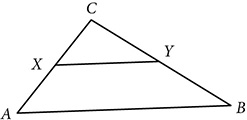
 This idea can be generalized to line segments that cut two sides in other ratios. If a line segment connects two sides of a triangle so that the sides are divided in the same ratio
This idea can be generalized to line segments that cut two sides in other ratios. If a line segment connects two sides of a triangle so that the sides are divided in the same ratio  , then the line segment is parallel to the third side of the triangle and its length is
, then the line segment is parallel to the third side of the triangle and its length is  of the third side. (See the proof of the Midsegment theorem and replace
of the third side. (See the proof of the Midsegment theorem and replace  with
with 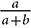 .)
.)
The converse of this generalized version is known as the Side-Splitter theorem.
 Side-Splitter theorem If a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
Side-Splitter theorem If a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
EXAMPLE
 The Angle Bisector theorem also talks about dividing a side of a triangle and creating proportional relationships.
The Angle Bisector theorem also talks about dividing a side of a triangle and creating proportional relationships.
 Angle Bisector theorem The bisector of an interior angle of a triangle divides the side opposite the angle into segments whose lengths are proportional to the adjacent sides.
Angle Bisector theorem The bisector of an interior angle of a triangle divides the side opposite the angle into segments whose lengths are proportional to the adjacent sides.
EXAMPLE
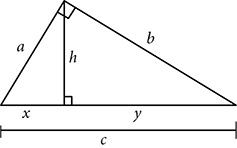
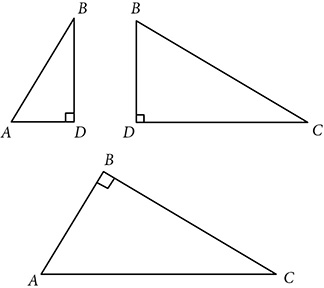
Altitude to the Hypotenuse
One of the special properties of any right triangle is that each leg is also an altitude. The altitude from the right angle vertex to the hypotenuse is not a side of the original triangle, but it comes with its own special properties.
The altitude to the hypotenuse of a right triangle divides the triangle into two right triangles, each of which is similar to the original triangle. The two smaller right triangles are similar to each other as well:
EXAMPLE
Finding the correct correspondence for the similarity statement can be a challenge however. The right angles must correspond, and those are at vertex D in the small triangles, but vertex B in the original. Then locate the smaller acute angle in each triangle. In ΔADB, the smallest angle is ∠B, but in ΔCDB, and in ΔABC, it’s ∠C.
Altitude 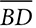 to the hypotenuse of ΔABC creates two right triangles, ΔADB and ΔCDB, which are similar to each other and to the original triangle, under the correspondence ΔABC ~ ΔADB ~ ΔBDC.
to the hypotenuse of ΔABC creates two right triangles, ΔADB and ΔCDB, which are similar to each other and to the original triangle, under the correspondence ΔABC ~ ΔADB ~ ΔBDC.
Corresponding sides are in proportion:

From those proportions come two rules about the lengths of segments, both involving the geometric mean. In a proportion like 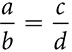 , b and c are the means. If both b and c are the same quantity, that quantity is the geometric mean. If
, b and c are the means. If both b and c are the same quantity, that quantity is the geometric mean. If  , then
, then 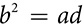 and
and  . Geometry deals with segment lengths so ignore negative square roots.
. Geometry deals with segment lengths so ignore negative square roots.
 The altitude to the hypotenuse is the geometric mean between the two segments of the hypotenuse.
The altitude to the hypotenuse is the geometric mean between the two segments of the hypotenuse.
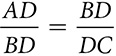
 Each segment of the hypotenuse is the geometric mean between the adjacent side and the whole hypotenuse.
Each segment of the hypotenuse is the geometric mean between the adjacent side and the whole hypotenuse.
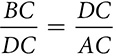
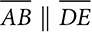 . Prove ΔABC ~ ΔDEC.
. Prove ΔABC ~ ΔDEC.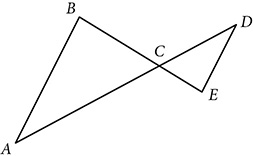
 . Prove ΔABC ~ ΔDEC.
. Prove ΔABC ~ ΔDEC.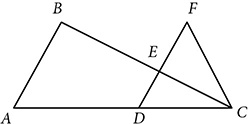
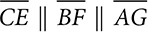 . Prove ΔCDE ~ ΔBDF.
. Prove ΔCDE ~ ΔBDF.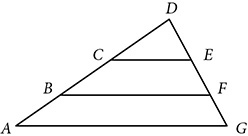
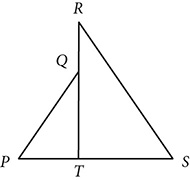
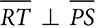 and ∠PQT ≅ ∠SRT. Prove
and ∠PQT ≅ ∠SRT. Prove 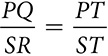 .
.
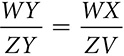
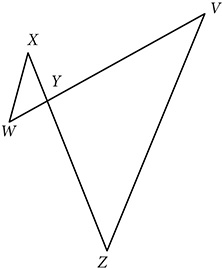
 is drawn in ΔADC and altitude
is drawn in ΔADC and altitude  is drawn in ΔJML. If ΔACD ~ ΔJLM, prove ΔABC ~ ΔJKL.
is drawn in ΔJML. If ΔACD ~ ΔJLM, prove ΔABC ~ ΔJKL.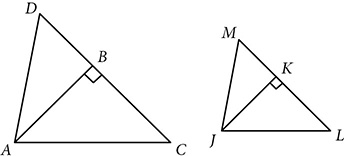
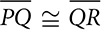 and ΔRST is isosceles with
and ΔRST is isosceles with 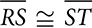 . If T is the midpoint of
. If T is the midpoint of 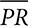 and
and 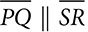 , prove that RS =
, prove that RS = 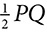 .
.

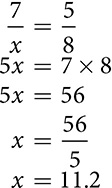
 .
.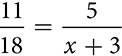 .
.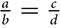 , shown in the properties above, (
, shown in the properties above, ( ,
, ,
,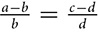 ) results in an equivalent equation after the Means-Extremes property is applied.
) results in an equivalent equation after the Means-Extremes property is applied.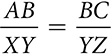 . If AB = 14, XY = 49, and YZ = 57, find BC.
. If AB = 14, XY = 49, and YZ = 57, find BC.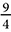 . If AB = 9 cm, how long is A′B′?
. If AB = 9 cm, how long is A′B′? . If X′Y′ = 156 cm and XZ = 110 cm, find the lengths of XY and X′Z′.
. If X′Y′ = 156 cm and XZ = 110 cm, find the lengths of XY and X′Z′.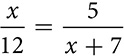 for a positive value of x. If this proportion expressed the proportional relationship of sides of similar triangles, what would the scale factor be?
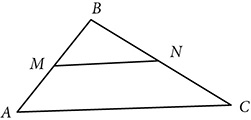
for a positive value of x. If this proportion expressed the proportional relationship of sides of similar triangles, what would the scale factor be?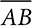 and N is the midpoint of
and N is the midpoint of 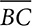 . M divides
. M divides 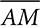 into
into  and
and 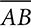 , each half as long as
, each half as long as 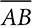 , and N divides
, and N divides 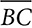 into
into 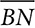 and
and  , each half of
, each half of 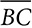 . Therefore,
. Therefore, 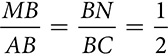 . Two pairs of corresponding sides are in proportion. ∠B is included between
. Two pairs of corresponding sides are in proportion. ∠B is included between 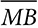 and
and 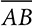 and
and 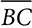 in ΔABC. Because ∠B is congruent to itself, ΔMBN ~ ΔABC by SAS. Because the triangles are similar, corresponding angles are congruent, and ∠A ≅ ∠BMN, and that proves that
in ΔABC. Because ∠B is congruent to itself, ΔMBN ~ ΔABC by SAS. Because the triangles are similar, corresponding angles are congruent, and ∠A ≅ ∠BMN, and that proves that 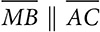 . Like the other sides of the two triangles,
. Like the other sides of the two triangles, 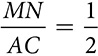 .
.
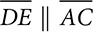 , then
, then 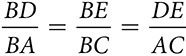 and
and  .
.
 . The proof of this one requires trigonometry, so we’ll save that for later.
. The proof of this one requires trigonometry, so we’ll save that for later.
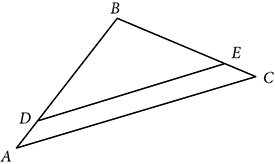
 in the triangle below, you can prove that
in the triangle below, you can prove that 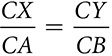 . Use properties of proportions to show that if
. Use properties of proportions to show that if 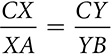 .
.
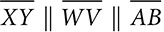 . Prove
. Prove 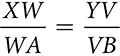 .
.
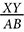 equal to
equal to  or
or  ? Explain your reasoning.
? Explain your reasoning.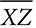 bisects ∠X. If XY = 3 inches, XW = 4 inches, and WY = 5 inches, find the length of
bisects ∠X. If XY = 3 inches, XW = 4 inches, and WY = 5 inches, find the length of 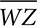 .
.
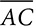 into two segments. AD = 32 cm and DC = 20 cm. If AB is 15 cm longer than BC, find the length of
into two segments. AD = 32 cm and DC = 20 cm. If AB is 15 cm longer than BC, find the length of 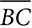 .
.
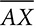 ,
, 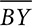 , and
, and 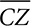 are angle bisectors and P is the incenter of the triangle. Explain why
are angle bisectors and P is the incenter of the triangle. Explain why 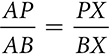 .
.