Chapter 10. Acids, Bases, and Buffers
Equipment and Materials
You’ll need the following items to complete this lab session. (The standard kit for this book, available from www.thehomescientist.com, includes the items listed in the first group.)
Materials from Kit
Goggles
Acetic acid solution
Ammonia solution
Beaker, 50 mL
Centrifuge tubes, 15 mL (5)
Hydrochloric acid solution
pH test paper
Pipettes
Reaction plate, 24-well
Reaction plate, 96-well
Sodium hydroxide solution
Stirring rod
Materials You Provide
Gloves
Marking pen
Paper towels
Scissors
Specimens: household materials (see Procedure III-1-3: pH of Household Materials)
Water, distilled
Background
Acids, bases, and buffers are fundamental components of the chemistry of life. All lifeforms use these chemicals in numerous essential life processes, from respiration to digesting food to maintaining the cellular environments necessary for life, to give just a few examples.
Living organisms use many different acids, bases, and buffers, from simple compounds to very complex organic molecules. For example, the gastric juice in your stomach is largely made up of one of the simplest of all acids, hydrochloric acid, while the DNA present in your cells is actually deoxyribonucleic acid, the most complex of all acids.
In this lab session, we’ll learn how biologists quantify these chemicals and examine some of the important characteristics of acids, bases, and buffers.
Procedure III-1-1: Percentage and Molar Concentrations
A solution is a mixture of two or more components, each of which may be a solid, liquid, or gas. The solute is the material being dissolved, and the solvent is the material that dissolves the solute. For example, if you add a teaspoon of sugar to a mug of tea, the sugar is the solute and the tea is the solvent.
Note
When solids are dissolved in liquids, the solids are always considered the solutes, regardless of the amount being dissolved. Otherwise, by convention, the material or materials present in the smaller amounts are considered to be the solute or solutes, while the material or materials present in the larger amounts are considered to be the solvent or solvents.
The concentration of a solution specifies the amount of solute per unit of solvent. There are many ways to specify concentration, but the five most widely used by biologists are weight-to-volume percentage, weight-to-weight percentage, volume-to-volume percentage, molarity, and molality.
- Weight-to-volume percentage
Weight-to-volume percentage, abbreviated w/v, is the number of grams of solute per 100 mL of solution. For example, a 1% w/v solution of methylene blue contains 1 gram of methylene blue dissolved in sufficient water to make up 100 mL of solution. W/v percentages are most often used for stains and other bench reagents that comprise a solid dissolved in water or alcohol. In recent texts this method is usually called mass-to-volume percentage, abbreviated m/v, although the older (and incorrect) weight-to-volume remains very widely used.
- Weight-to-weight percentage
Weight-to-weight percentage, abbreviated w/w or m/m, is the number of grams of solute per per 100 grams (not mL) of solution. For example, a 36% w/w solution of hydrochloric acid contains contains 36 grams of hydrochloric acid gas per 100 grams of solution. Note that the w/w percentage may differ significantly from the w/v percentage because the density of the solution may be greater or less than 1.00 grams/mL. W/w percentages are most often used for gases dissolved in water, such as hydrochloric acid, ammonia, and formaldehyde. This makes it easy to obtain a specific amount of the chemical by simple weighing. For example, if you need 3.6 grams of hydrochloric acid, you can get it simply by weighing out 10.0 grams of the 36% solution.
- Volume-to-volume percentage
Volume-to-volume percentage, abbreviated v/v, is ordinarily used for solutions that contain water and another miscible liquid such as ethanol, isopropanol, or acetone, but is sometimes used to specify the concentration of an aqueous solution of a gas. V/v percentage is simply the number of mL of solute per 100 mL of solution. For example, a 70% v/v solution of isopropanol contains 70 mL of pure isopropanol mixed with water to make 100 mL of total solution. We phrased that very carefully, because volumes are not necessarily additive and are often greater or less than you might expect. For example, mixing 70 mL of pure isopropanol with 30 mL of pure water does not yield 100 mL of solution.
The preceding three methods of specifying concentration are common, but all of them share a disadvantage. They are based on the mass or volume of solute present in the solution, but do not take into account the fact that different solute molecules have different molecular masses. Molecules react with each other in fixed ratios based on the number of molecules rather than their masses or volumes. For example, two molecules of sodium hydroxide, NaOH, react with one molecule of sulfuric acid, H2SO4, to form one molecule of sodium sulfate, Na2SO4 and two molecules of water, H2O, by the following balanced equation.
2 NaOH + H2SO4 → Na2SO4 + 2 H2O
One mole of any chemical compound contains the same number of molecules, so it’s also correct to say that two moles of sodium hydroxide react with one mole of sulfuric acid to produce one mole of sodium sulfate and two moles of water. Because the molecular mass of different compounds varies, the mass of one mole of different compounds also varies.
Six of One, 60,000,000,000,000,000,000,000 Dozen of the Other
Mole is a group noun, like dozen or gross but larger. How much larger? If you have a dozen eggs, you have 12 eggs; if you have a gross of microscope slides, you have 144 slides; if you have a mole of molecules, you have 6.0 x 1023 (6 followed by 23 zeros) or 60 sextillion dozen molecules.
The mass of one mole of sodium hydroxide is 40.00 grams. (You can also say that the molar mass of sodium hydroxide is 40.00 g/mol.) The mass of one mole of sulfuric acid is 98.07 grams. So, for any procedure that involves reacting chemicals with each other, it’s much more convenient to specify concentrations in terms of moles rather than with mass or volume percentages.
For example, if you want to react a 10% w/v solution of sodium hydroxide with a 10% w/v solution of sulfuric acid to produce pure sodium sulfate without an excess of either reactant, you have some calculating to do to get the mole ratios to come out right. On the other hand, if the concentrations of your solutions are specified in moles, the calculations are trivially simple. That brings up the final two methods of specifying concentration that are widely used by biologists.
- Molarity
Molarity, abbreviated mol/L or M, is the number of moles of solute per per liter of solution. For example, a solution that contains 6 moles of solute per liter of solution is 6 molar, usually abbreviated 6 M.
Chemists usually use fractional molarities to refer to solutions less concentrated than 1 M. For example, a chemist would probably refer to a 0.1 M solution as “tenth-molar” and a 0.01 M solution as “hundredth-molar.” Biologists often work with much more dilute solutions than chemists—down into the 0.00001 M range or less—so biologists often specify concentrations in millimoles/L (0.001 mol/L, or millimolar, abbreviated mM) or micromoles/L (0.000001 mol/L, or micromolar, abbreviated μM). A 1 M solution is 1,000 mM and 1,000,000 μM.
SI Versus the Real World
The term molarity is officially deprecated; the official SI unit is moles of substance per cubic meter, abbreviated mol/m3. That value is too large to be practical—a 1 molar solution contains 1,000 moles of solute per cubic meter—but young, pedantic scientists sometimes use the unofficial SI-like unit moles of substance per cubic decimeter, abbreviated mol/dm3, which has the same value as molarity. That is, a 1 molar solution contains 1 mole of solute per cubic decimeter of solution.
In practice, particularly in the United States, most scientists continue to use the old-style terminology. The word molar is simply too useful to give up in favor of the long, awkward official SI terminology.
- Molality
Molality, abbreviated mol/kg or m, is the number of moles of solute per kilogram of solvent. For example, a solution that contains 6 moles of solute per kilogram of solvent is 6 molal, usually abbreviated 6 m. Molality is useful when working with procedures that involve the colligative properties of solutions, such as diffusion and osmosis.
Molarity Versus Molality
Remember the difference between molarity and molality. Molarity specifies the number of moles of solute per liter of solution. Molality specifies the number of moles of solute per kilogram of solvent (not solution). At low concentrations in aqueous solutions, the values for molarity and molality are very similar. In concentrated solutions, or those using a solvent other than water, the two values may differ dramatically.
To continue our example from above, a six molar (6 M) solution of sodium hydroxide contains 240.0 grams (6 moles) of sodium hydroxide per liter of solution, and a 1 M solution of sulfuric acid contains 98.07 grams (1 mole) of sulfuric acid per liter of solution. Since we know that two moles of sodium hydroxide react with one mole of sulfuric acid, if you are using these molar solutions you can simply mix one volume of the 6 M sodium hydroxide solution with three volumes of the sulfuric acid solution to produce a pure solution of sodium sulfate, without either reactant in excess.
Similarly, if you need 1 M sodium hydroxide, you can simply dilute one volume of the 6 M sodium hydroxide solution with five volumes of distilled water. As it happens, we need to do exactly that to produce solutions that we’ll use later in this lab session.
Making Up 1 M Solutions
For the following procedure, we’ll need 1 molar solutions of acetic acid, ammonia, hydrochloric acid, and sodium hydroxide. The following instructions assume you are using the 6 M solutions supplied with the kit. If you are using chemicals from another source, dilute them appropriately. For example, if you are using concentrated (12 M) hydrochloric acid, add one part of the acid to 11 parts distilled water to make up a 1 M solution. If you are using solid sodium hydroxide, dissolve 4.00 grams of the solid in about 80 mL of water and make up the solution to 100 mL. (Warning: adding concentrated acids or bases to water produces considerable heat and may cause the solution to boil and spatter. Take care to avoid being burned or splashed.)
Note
Pure distilled water has a pH of 7.0. Unfortunately, distilled water absorbs carbon dioxide gas from the air to form carbonic acid, so the pH of distilled water that has been standing in an open container can be significantly lower than 7.0. To ensure that your distilled water actually has a pH close to neutral, either use a freshly opened bottle or boil the distilled water for a couple of minutes to drive off the dissolved carbon dioxide and then allow it to cool in a covered container.
If you have not already done so, put on your goggles, gloves, and protective clothing. Warning: The concentrated solutions you’ll be using are extremely corrosive.
Using a clean pipette, transfer 1.25 mL of distilled water to each of four centrifuge tubes or other small containers labeled “1 M acetic acid,” “1 M ammonia,” “1 M hydrochloric acid,” and “1 M NaOH.”
Using clean pipettes each time, transfer 0.25 mL of the corresponding 6 M solutions to each of the labeled containers. Swirl or stir the containers to mix the solutions, and replace the caps.
Retain all of these solutions for use later in this lab session.
Procedure III-1-2: Effect of Concentration on pH
Acids and bases are key components of the chemistry of life. For our purposes, we can consider an acid to be any chemical that, when dissolved in water, increases the concentration of hydrogen ions (H+) of the solution. (Actually, a free hydrogen ion immediately reacts with a water molecule, H2O, to form a hydronium ion, H3O+, but the effect is the same.) A base is any chemical that, when dissolved in water, increases the concentration of the hydroxide ion, OH-.
In pure water, only a tiny percentage of water molecules dissociate to form hydrogen ions and hydroxide ions. In any aqueous solution, including pure water, the product of the concentrations of the hydrogen and hydroxide ions is 10-14.
[H+] · [OH-] = 10-14
In pure water, the concentrations of the hydrogen and hydroxide ions are equal, at 10-7 molar, or one ten-millionth molar.
[10-7] · [10-7] = 10-14
If you add an acid to the water to increase the hydrogen ion concentration to, say, 10-4, a tiny percentage of those additional hydrogen ions react with hydroxide ions to form water molecules, thereby reducing the hydroxide ion concentration.
[H+] · [OH-] = 10-14
[10-4] · [10-10] = 10-14
In other words, adding the acid to the water increased the concentration of hydrogen ions from 0.0000001 molar to 0.0001 molar, while at the same time reducing the concentration of hydroxide ions from 0.0000001 molar to 0.0000000001 molar.
Obviously, such tiny numbers are inconvenient to deal with, so chemists use the pH scale to quantify the acidity or basicity of a solution. The pH of a solution is the negative base-10 log of its hydrogen ion concentration. So, for example, if the hydrogen ion concentration of a solution is 10-4, that solution’s pH is:
-log10(10-4) = 4
A neutral solution, one that is neither acidic nor basic, has a pH of 7. Pure water is neutral. An acid solution has a pH lower than 7, and a basic solution has a pH higher than 7. Each pH unit corresponds to a ten-fold increase or decrease in acidity or basicity. For example, a solution with a pH of 4 is ten times more acidic than a solution with a pH of 5, and a solution with a pH of 12 is ten times more basic than a solution with a pH of 11. Although the pH scale is often thought of as extending from 0 to 14, it’s actually open-ended. A concentrated solution of a strong acid can have a pH lower than 0, and a concentrated solution of a strong base can have a pH higher than 14.
In this procedure, we’ll prepare various dilutions of two acids, acetic and hydrochloric, and two bases, ammonia and sodium hydroxide. We’ll then use pH test paper to determine the pH of each of these solutions.
Populating the Reaction Plate
The first step is to populate the reaction plate with various dilutions of the four solutions whose pH we’ll be testing. We’ll use a procedure called serial dilution to produce ten-fold dilutions from each well to the next. For example, well A1 will contain 1.0 M acetic acid, well B1 0.1 M acetic acid, well C1 0.01 M acetic acid, and so on.
Fill the clean 50 mL beaker nearly full with distilled water.
Using a clean pipette, transfer nine drops of distilled water to each of wells B1 through H1, B3 through H3, B5 through H5, and B7 through H7 of the reaction plate.
Use a clean pipette to transfer a few drops of 1 M acetic acid to well A1 and one drop of 1 M acetic acid to well B1. Return any acid still in the pipette to the labeled container.
Use the pipette to draw up and expel the contents of well B1 several times to ensure the solution is thoroughly mixed. Well B1 now contains one drop of 1 M acetic acid mixed with nine drops of distilled water, which produces 0.1 M acetic acid.
Transfer one drop of the solution from well B1 to well C1. Return any solution remaining in the pipette to well B1, and use the pipette to mix the solution in well C1 thoroughly. Well C1 now contains one drop of 0.1 M acetic acid and nine drops of water, for a concentration of 0.01 M.
Repeat the serial dilution for the remaining wells in column 1. When you finish you’ll have eight wells populated, A1 through H1, with acetic acid dilutions of 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, and 0.0000001 M, respectively.
Using a clean pipette, repeat the serial dilution procedure with ammonia in rows A through H of column 3 to produce final dilutions of 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, and 0.0000001 M, respectively.
Using a clean pipette, repeat the serial dilution procedure with hydrochloric acid in rows A through H of column 5 to produce final dilutions of 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, and 0.0000001 M, respectively.
Using a clean pipette, repeat the serial dilution procedure with sodium hydroxide in rows A through H of column 7 to produce final dilutions of 1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, and 0.0000001 M, respectively.
Retain the beaker of distilled water and the leftover 1 M solutions for use later in this lab session.
Determining the pH of the Solutions
With the reaction plate populated with acids and bases at various concentrations, the next step is to determine pH values for each of those solutions.
Use scissors to quarter eight strips of pH test paper. You’ll need 32 pieces of pH test paper, one for each of the occupied wells.
Being careful not to slosh solution from one well into another, dip the tip of the stirring rod into well H1 (the most dilute acetic acid solution) and touch the tip of the rod to a piece of pH test paper to transfer the drop of acid to the paper. Compare the color of the test paper to the color chart and estimate the pH of that solution as closely as possible. Record that value in your lab notebook.
Dip the tip of the stirring rod into the beaker of distilled water to rinse it. Dry the stirring rod with a clean paper towel.
Repeat steps 2 and 3 to test each of the remaining wells in columns 1, 3, 5, and 7.
The actual pH values you observe and record may vary slightly from expected values, particularly at the mid-range pH levels, depending on how accurate your serial dilutions were and how accurately you interpret the colors of the pH test paper.
Hydrochloric acid is a strong acid and sodium hydroxide is a strong base, which means they fully dissociate in solution to form hydrogen ions and hydroxide ions, respectively. The 1 M hydrochloric acid should have a pH value of 0, with each succeeding ten-fold dilution increasing that value by 1. Similarly, the 1 M sodium hydroxide should have a pH value of 14, with each ten-fold dilution decreasing that value by 1.
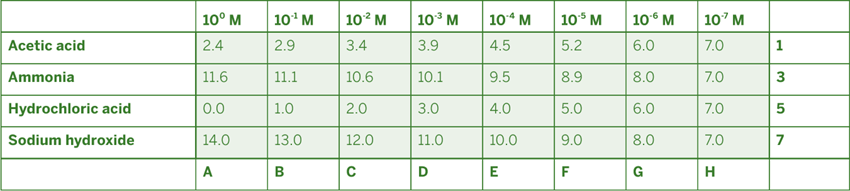
Acetic acid is a weak acid and ammonia is a weak base, which complicates matters. In concentrated solutions, neither of these chemicals dissociates fully, so the pH of the acetic acid solution is higher than you might expect, and the pH of the ammonia solution lower. Figure 10-1 lists the theoretical pH values for various concentrations of these four chemicals, from 100 molar (1 molar) to 10-7 molar (0.0000001 molar).
Note that in the most dilute solutions, the pH values for the weak acid and weak base are very close to those of the corresponding strong acid and strong base. In such dilute solutions, the weak acid or base is sufficiently dissociated to provide enough hydronium or hydroxide ions to establish the pH at the expected level. Conversely, as the concentration increases, the pH values begin to diverge. In the highest concentration, 1 M, the weak acetic acid has a pH of only 2.4, versus the 0.0 pH of the strong and therefore fully dissociated hydrochloric acid. Similarly, in a 1 M solution, the weak base ammonia has a pH of only 11.6, versus the 14.0 pH of the strong and therefore fully dissociated sodium hydroxide. This difference in behavior between strong and weak acids and bases has profound implications for the chemistry of life.
Procedure III-1-3: pH of Household Materials
To move our study of pH into a more familiar realm, let’s take a few minutes to test the pH of common household materials. If the materials are liquids, test them directly. For solids, dissolve a tiny amount in a few drops of water in a reaction plate. Quarter pH test strips, and use a fresh strip for each material.
Here are some materials you might test: water (distilled, tap, and bottled), saliva, urine, table salt, table sugar, baking soda, mouthwash, alcohol or hand sanitizer, washing soda, laundry detergent, chlorine bleach, toilet cleaner, drain opener, window cleaner, soap, shampoo, juices (apple, grape, grapefruit, etc.), vinegar, soft drinks (carbonated and uncarbonated), coffee and tea (with and without milk and/or sugar), and milk.
Record your observations in your lab notebook, along with any conclusions you make concerning the range of pH values found in food and other biological materials versus those intended for cleaning and similar purposes.
Procedure III-1-4: Buffers
As we learned in the first procedure, even a tiny amount of acid or base can have a major effect on the pH of a solution, particularly if the pH of that solution is originally neutral or nearly so. For example, adding one drop of 1 M hydrochloric acid to nine drops of distilled water reduces the pH from 7 to 1; adding one drop to 99 drops of water reduces the pH from 7 to 2; and adding one drop to 999 drops of water reduces the pH from 7 to 3.
Such large variations in pH are incompatible with the biological processes of life. For example, many enzymes function only within an extremely narrow pH range, and are denatured (destroyed) if exposed to a pH much outside that range. Living things avoid these extremes in pH by using buffers, which resist changes in pH. Human blood plasma is one example of a buffer. It ordinarily maintains a pH of 7.40 ± 0.05. If the pH of someone’s blood plasma is outside the range of about 7.3 to 7.5, that person is ill; if the pH is much outside that range, the person is dead.
A buffer solution is a mixture of a weak acid and a strong base or (more rarely) a weak base and a strong acid. For example, acetic acid (a weak acid) reacts in solution with sodium hydroxide (a strong base) to produce sodium acetate. A pure solution of sodium acetate is fully dissociated into sodium ions and acetate ions, and has an alkaline (basic) pH. But if you mix that sodium acetate solution with additional acetic acid—which does not dissociate fully in solution—you produce a solution that contains sodium ions, acetate ions, and molecular (nondissociated) acetic acid.
If you add a small amount of a strong acid to this acetate buffer solution, it absorbs the additional hydrogen ions by forming additional acetic acid molecules from those hydrogen ions and free acetate ions. If you instead add a small amount of a strong base to the acetate buffer solution, it absorbs the additional hydroxide ions by breaking down acetic acid molecules into hydrogen ions and acetate ions. The newly freed hydrogen ions react with the excess hydroxide ions to form neutral water molecules. In either case, the pH of the solution changes only slightly.
In this procedure, we’ll prepare a buffer solution and test its ability to resist pH changes as we add small amounts of a strong acid and a strong base.
Preparing a 0.1 M Acetate Buffer Solution
The first step is to prepare a 0.1 M acetate buffer solution. That solution will be 0.1 M with respect to sodium acetate and 0.1 M with respect to acetic acid and will have a pH just under 5.0. We’ll use 6 M solutions of acetic acid and sodium hydroxide to make up the buffer.
Because one mole of acetic acid reacts with one mole of sodium hydroxide to form one mole of sodium acetate, we’ll need to use twice as much acetic acid as sodium hydroxide. (Half of the acetic acid reacts with sodium hydroxide to form sodium acetate, and the other half of the acetic acid remains in solution as acetic acid.) Because a 6 M solution is 60 times more concentrated than our target 0.1 M concentration, we’ll need to dilute the solutions by using one part 6 M sodium hydroxide and two parts 6 M acetic acid to 57 parts of water.
If you have not already done so, put on your goggles, gloves, and protective clothing.
Label a 15 mL centrifuge tube “acetate buffer” and transfer 10 or 12 mL of distilled water to the tube.
Use a clean pipette to transfer 0.25 mL of 6 M sodium hydroxide solution to the tube. Swirl to mix the solution.
Use a clean pipette to transfer 0.50 mL of 6 M acetic acid to the tube. Swirl to mix the solution.
Fill the tube to the 15 mL line with distilled water. Cap the tube and invert it several times to mix the solution.
Testing the Buffer Solution
With the acetate buffer prepared, the next step is to test its resistance to changes in pH and compare that resistance to that of a nonbuffer solution (ordinary water). We’ll use the 1 M solutions of hydrochloric acid and sodium hydroxide we prepared earlier in this lab session.
If you have not already done so, put on your goggles, gloves, and protective clothing.
Use scissors to quarter 8 or 10 pH test paper strips.
Use a clean pipette to transfer 2.0 mL of water to each of wells A1 and D1 of the 24-well reaction plate and 2.0 mL of acetate buffer solution to each of wells B1 and C1 of the reaction plate.
Add one drop of 1 M hydrochloric acid to well A1. Stir the contents of the well with the stirring rod, and use the tip of the stirring rod to transfer one drop of the contents to a piece of test paper. Record your results in your lab notebook.
Using a fresh piece of test paper each time, repeat step 4 until you have added a total of five drops of 1 M hydrochloric acid to well A1.
Repeat steps 4 and 5, but this time adding 1 M sodium hydroxide to well D1.
Repeat steps 4 and 5, but this time adding the 1 M hydrochloric acid dropwise to well B1, which contains buffer solution. Continue adding acid to well B1 until the pH starts to show a sharp decrease, or until you run out of acid.
Repeat steps 4 and 5, but this time adding the 1 M sodium hydroxide dropwise to well C1, which contains buffer solution. Continue adding base to well C1 until the pH starts to show a sharp increase, or until you run out of base.
Note the key difference between a buffer solution and an unbuffered solution such as water. An unbuffered solution reacts to the addition of small amounts of a strong acid or strong base by showing large changes in pH. A buffer solution absorbs small quantities of a strong acid or strong base without much change in pH. Note also that the capacity of a buffer is limited. Adding larger amounts of a strong acid or strong base eventually overwhelms the ability of the buffer solution to resist changes in pH. Once the buffer solution reaches its capacity, it behaves as an ordinary, unbuffered solution.
Review Questions
Q1: How would you make up 100 mL of 1 M potassium iodide solution?
Q2: You need to make up 1 L of 1 M sulfuric acid. Your concentrated sulfuric acid is 98% sulfuric acid and has a density as 1.84 g/mL. Describe two methods for making up the 1 M solution.
Q3: You have a hydrochloric acid solution with a known pH of 3.00. How much of that solution would you dilute with distilled water to a final volume of 1 L to produce a 100 μM (micromolar) solution? What would the pH of that solution be? (Assume complete dissociation of the acid.)
Q4: How did the pH values you observed for food and other material intended for human consumption differ from the pH values of household cleaners and similar items?