In Chapter 3, we took a brief look at certain update anomalies that can be caused by FDs: specifically, FDs that hold in a relvar that’s not in BCNF. To be frank, however, the update anomaly concept was never very precisely defined (at least, not in that context); probably the best that could be said about it is that the update anomaly problem is just the redundancy problem looked at from another point of view. So what about JDs?—specifically, JDs that hold in a relvar that’s not in 5NF? Such JDs do cause redundancy, as we’ve seen, and so we can expect them to give rise to update anomalies as well. And indeed they do; what’s more, the concept can be (or at any rate, is) more precisely defined in that context, as we’ll see.
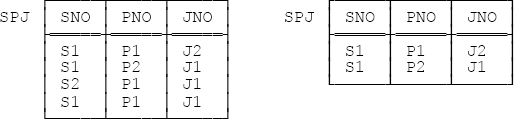
Consider Figure 10-2, which shows two possible values for relvar SPJ; the one on the left is a repeat of the relation from Figure 10-1, the one on the right is obtained from the one on the left by removing two tuples.
Observe now that if the current value of relvar SPJ is the relation on the left of the figure, there’s a deletion anomaly: We can’t delete just the tuple (S1,P1,J1), because what results after that deletion violates the JD and is thus not a legal value for the relvar. Likewise, if the current value of relvar SPJ is the relation on the right of the figure, there’s an insertion anomaly: We can’t insert just the tuple (S2,P1,J1), because what results after that insertion is (again, and for the same reason) not a legal value for the relvar.
Now, the JD in this example is tuple forcing. (Recall from Chapter 9 that a JD is tuple forcing if it’s such that, if certain tuples appear, certain additional tuples are forced to appear as well.) And the notion of tuple forcing JDs (or the intuition behind that notion, rather) allows us to give definitions of the kinds of update anomalies that can occur in the presence of such a JD—definitions that are more precise than their FD counterparts (such as they are).[104] To be specific:
Definition: Let the JD J hold in relvar R. Then R suffers from a deletion anomaly with respect to J if and only if there exist a relation r and a tuple t, each with the same heading as R, such that:
r satisfies J, and
The relation r′ whose body is obtained from that of r by removing t violates J.
Definition: Let the JD J hold in relvar R. Then R suffers from an insertion anomaly with respect to J if and only if there exist a relation r and a tuple t, each with the same heading as R, such that:
r satisfies J, and
The relation r′ whose body is obtained from that of r by appending t satisfies R’s key constraints but violates J.
Points arising:
Note carefully that the foregoing anomalies are specifically defined in terms of some JD J, and they can certainly occur if J is tuple forcing, as we’ve seen. In Chapter 13, however, we’ll see that a relvar can suffer from an insertion anomaly (though not a deletion anomaly) with respect to J even if J isn’t tuple forcing.
Although they’re more precisely defined than their FD counterparts, the foregoing anomalies can still be regarded as the redundancy problem looked at from another point of view—though here, of course, we’re referring to redundancy caused by a JD, not by an FD.
If relvar R is subject to update anomalies and those anomalies are caused by a JD (tuple forcing or otherwise), then replacing R by a set of 5NF projections will solve the problem. That is, such anomalies can’t occur with a 5NF relvar.
Please note carefully, however, that not all update anomalies are caused by FDs and JDs. In fact, it’s probably true to say that most integrity constraints (though not all) can give rise to an insertion anomaly, in the sense that there always exists a tuple whose insertion would cause the constraint in question to be violated. (As a simple example, suppose there’s a constraint to the effect that supplier status values must lie in the range 1 to 100, inclusive.) By contrast, comparatively few constraints can give rise to a deletion anomaly. (One that does would be a constraint to the effect that there must always be at least two distinct suppliers. Another is a foreign key constraint; in the suppliers-and-parts database, for example, deleting a supplier can’t be done if it causes the pertinent foreign key constraint to be violated).
[104] They might be more precise, but they’re also slightly suspect, inasmuch as they talk about inserting or deleting an individual tuple. As explained in SQL and Relational Theory, INSERT and DELETE really work on entire relations, not on individual tuples.