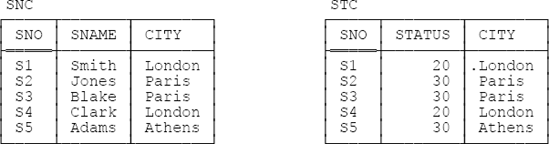
For simplicity, suppose the FD {CITY} →{STATUS} does not hold in relvar S (please note that I’ll stay with this assumption throughout the present chapter). Consider the following decomposition of that relvar:
SNC { SNO , SNAME , CITY }
KEY { SNO }
STC { SNO , STATUS , CITY }
KEY { SNO }Sample values are shown in Figure 14-1. As the figure shows, this decomposition is hardly very sensible (in particular, note that the fact that a given supplier is located in a given city appears twice), and yet it abides by all of the normalization principles—both projections are in 5NF; the decomposition is nonloss; dependencies are preserved; and both projections are needed in the reconstruction process.
Intuitively, the problem with the foregoing design is obvious: The tuple (s,n,c) appears in SNC if and only if the tuple (s,t,c) appears in STC; equivalently, the tuple (s,c) appears in the projection of SNC on SNO and CITY if and only if that very same tuple (s,c) appears in the projection of STC on SNO and CITY. To state the matter a trifle more formally, we can say the design is subject to the following equality dependency (EQD)—
CONSTRAINT ... SNC { SNO , CITY } = STC { SNO , CITY } ;—and this EQD makes the redundancy explicit.
To repeat, however, the foregoing design abides by all of the well established principles of normalization. It follows that those principles by themselves aren’t enough—we need something else to tell us what’s wrong with this design (something else formal, that is; we all know what’s wrong with it informally). To put the matter another way, the normalization discipline provides a set of formal principles to guide us in our attempts to reduce redundancy, but that set of principles by itself is inadequate, as the example plainly shows. We need another principle. In other words, as I’ve said more than once in this book already, we need more science.