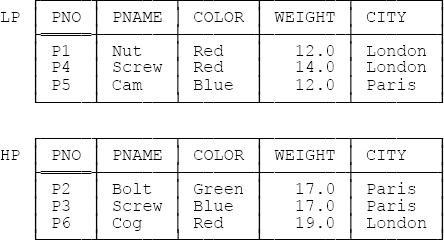
In order to see what the principle we need might look like, let’s consider a simpler example. As you know, normalization as such—in particular, normalization as used in the example of the previous section—has to do with “vertical” decomposition of relvars (meaning decomposition via projection). But “horizontal” decomposition (that is, decomposition via restriction) is clearly possible, too. Consider the design illustrated in Figure 14-2, in which the parts relvar P has been split horizontally—in fact, partitioned—into two relvars, one (“light parts,” LP) containing parts with weight less than 17.0 pounds and the other (“heavy parts,” HP) containing parts with weight greater than or equal to 17.0 pounds. (I assume for definiteness that WEIGHT values represent weights in pounds avoirdupois.)
The predicates are as follows:
LP: Part PNO is named PNAME, has color COLOR and weight WEIGHT (which is less than 17.0), and is stored in city CITY.
HP: Part PNO is named PNAME, has color COLOR and weight WEIGHT (which is greater than or equal to 17.0), and is stored in city CITY.
Note that the original relvar P can be recovered by taking the (disjoint) union of relvars LP and HP.
Why might we want to perform such a horizontal decomposition? Frankly, I’m not aware of any good logical reason for doing so, though of course that’s not to say no such reason exists. Be that as it may, observe that we can, and should, state two constraints that apply to these relvars:
CONSTRAINT LPC AND ( LP , WEIGHT < 17.0 ) ;
CONSTRAINT HPC AND ( HP , WEIGHT ≥ 17.0 ) ;(I remind you from Chapter 2 that the Tutorial D expression AND(rx,bx), where rx is a relational expression and bx is a boolean expression, returns TRUE if and only if bx evaluates to TRUE for every tuple in the relation denoted by rx.)
So we have here a slightly unusual situation: To be specific, in the case of relvars LP and HP, part of the predicate can, and should, be captured formally in the shape of explicit constraints. Indeed, the very fact that such constraints need to be stated and enforced might be seen as militating against the design. But even if horizontal decomposition is contraindicated at the logical level, there are still plenty of pragmatic reasons (having to do with recovery, security, performance, and other such matters) for such a decomposition at the physical level; hence, given that the logical and physical levels tend to be in lockstep, pretty much, in today’s DBMSs—i.e., there’s not nearly as much data independence in those DBMSs as there ought to be—it follows that there are likely to be pragmatic reasons for performing such a decomposition at the logical level as well, at least in current products.
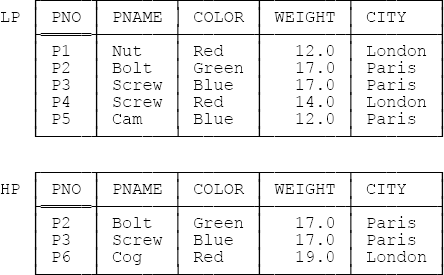
Now, regardless of what you might think of the foregoing argument, at least there’s nothing obviously bad about the design of Figure 14-2 (well, let’s agree as much for the sake of the example, at any rate).[141] But suppose we were to define relvar LP just a little differently; to be specific, suppose we defined it to contain those parts with weight less than or equal to 17.0 pounds (adjusting the predicate and constraint LPC accordingly, of course). Figure 14-3 below is a revised version of Figure 14-2, showing what happens with this revised design. As you can see, now there definitely is something bad; to be specific, the tuples for parts P2 and P3 now appear in both relvars in Figure 14-3 (in other words, there’s now some redundancy). What’s more, those tuples must appear in both relvars! For suppose, contrariwise, that (say) the tuple for part P2 appeared in HP and not in LP. Then, noting that LP contains no tuple for part P2, we could legitimately conclude from The Closed World Assumption—see Chapter 2—that it’s not the case that part P2 weighs 17.0 pounds. But then we see from HP that part P2 in fact does weigh 17.0 pounds, and the database is thus inconsistent, because it contains a contradiction. (Inconsistency in a database is highly undesirable, of course. As I show in SQL and Relational Theory, you can never trust the results you get from an inconsistent database; in fact, you can get absolutely any result whatsoever—even results asserting nonsensical things like 0 = 1—from such a database!)
Now, the problem with the design of Figure 14-3 is easy to see: The predicates for LP and HP “overlap,” in the sense that the very same tuple t can satisfy both of them. What’s more, if t is such a tuple, and if at some given time that tuple t represents a “true fact,” then, in accordance with The Closed World Assumption, that tuple t must necessarily appear in both relvars at the time in question (whence the redundancy, of course). In fact, we have another EQD on our hands:
CONSTRAINT ... ( LP WHERE WEIGHT = 17.0 ) =
( HP WHERE WEIGHT = 17.0 ) ;To say it again, the problem in the example is that we’ve allowed two relvars to have overlapping predicates. Clearly, then, the principle we’re looking for is going to say something along the lines of: Don’t do that! Let’s try and state the matter a little more precisely:
Definition (first attempt): The Principle of Orthogonal Design says that if relvars R1 and R2 are distinct, then there must not exist a tuple with the property that if it appears in R1, then it must also appear in R2 and vice versa.[142] Note: The term orthogonal here derives from the fact that what the principle effectively says is that relvars should be independent of one another—which they won’t be, if their meanings overlap in the foregoing sense.
In what follows, I’ll sometimes abbreviate the foregoing principle (or, rather, various versions of that principle) to just the orthogonality principle, or sometimes just to orthogonality.
Aside: As elsewhere in this book, I might be accused of practicing a tiny deception in the foregoing. Take another look at Figure 14-3; in particular, take a look at the tuple for part P2. That tuple appears in both LP and HP because it represents a true instantiation of the predicate for LP and a true instantiation of the predicate for HP. Or does it? The instantiations of those predicates for part P2 are actually as follows:
LP: Part P2 is named Bolt, has color Green and weight 17.0 (which is less than or equal to 17.0), and is stored in city Paris.
HP: Part P2 is named Bolt, has color Green and weight 17.0 (which is greater than or equal to 17.0), and is stored in city Paris.
These two propositions aren’t the same! Of course, they’re certainly equivalent to one another—but in order to recognize that equivalence, we need to know that “17.0 ≤ 17.0” and “17.0 ≥ 17.0” are both true, and then we need to apply a little logical reasoning. (The point is, what’s obvious to us as human beings isn’t necessarily obvious to a machine, and for completeness I really ought to have spelled out the missing steps in my argument.) End of aside.
Now, adherence to the orthogonality principle in the light vs. heavy parts example would certainly avoid the redundancies illustrated in Figure 14-3. Note, however, that the principle as stated applies only to relvars like LP and HP that have the very same heading, because of course it’s impossible for the same tuple to appear in two different relvars if the relvars in question have different headings. Thus, you might be thinking the orthogonality principle isn’t much use, because it’s probably unusual in practice to have two relvars in the same database with the same heading.[143] And I would probably agree with you, if that were all there was to it; I mean, in that case life would be fairly simple and this chapter could stop right here (it might not even be worth dignifying such a very obvious rule with the rather grand label “principle”). But, of course, there’s quite a lot more to be said on the matter. In order to explore the possibilities further, I first need to take a closer look at the relationship between tuples and propositions.
[141] Actually there might be something bad. Consider, for example, what has to happen if the weight of part P1 is doubled.
[142] That “and vice versa” is important. Consider a revised version of the suppliers-and-parts database, in which (a) attribute QTY is dropped from relvar SP and (b) another relvar, SAP, with heading {SNO,PNO} and predicate Supplier SNO is able to supply part PNO is added. Then there might well be a constraint to the effect that a given tuple can appear in SP only if it also appears in SAP, and such a reasonable state of affairs doesn’t (and obviously shouldn’t) constitute a violation of orthogonality.
[143] In this chapter, unlike previous chapters, the fact that the heading concept includes the pertinent attribute types is sometimes important; thus, the term heading must be (re)interpreted accordingly, where it makes any difference. By way of example, the headings {PNO CHAR, WEIGHT RATIONAL} and {PNO CHAR, WEIGHT INTEGER}, though they involve the same attribute names, aren’t the same heading, precisely because the two WEIGHT attributes are of different types. All of that being said, for simplicity I’ll continue to ignore attribute types as much as I can throughout the rest of the chapter.