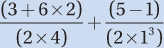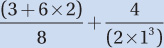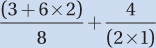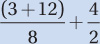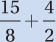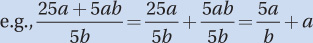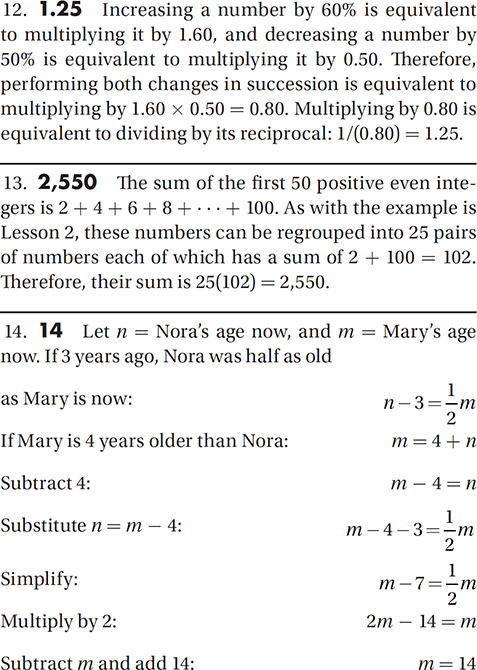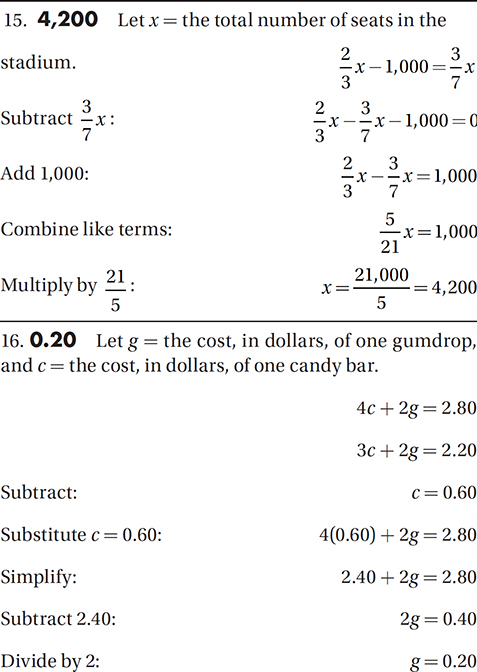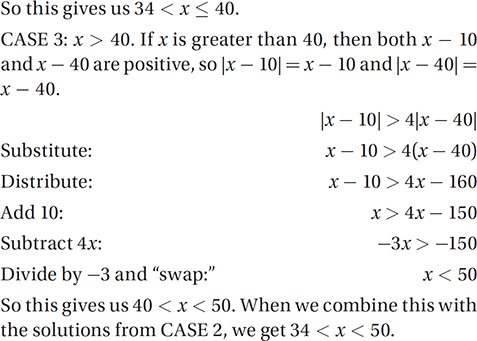CHAPTER 7
2. Working with Linear Equations
3. Working with Inequalities and Absolute Values
4. Working with Linear Systems
The SAT Math: Heart of Algebra
Why is algebra so important on the SAT Math test?
About 36% (21 out of 58) of the SAT Math questions fall under the category called the “Heart of Algebra.” Questions in this category test your ability to
analyze, fluently solve, and create linear equations, inequalities, [and] systems of equations using multiple techniques.
These questions will also assess your skill in
interpreting the interplay between graphical and algebraic representations [and] solving as a process of reasoning.
The specific topics include
• creating and solving linear equations in one and two variables
• graphing and interpreting linear equations
• creating, interpreting, and solving linear systems
• graphing and solving inequalities and systems of inequalities
• interpreting and solving algebraic word problems
Why are these skills important?
Algebra is an essential tool of quantitative analysis not only in math but also in subjects like engineering, the physical sciences, and economics. When describing the relationships between or among different quantities, or exploring the nature of unknown quantities, algebra provides essential tools for analyzing and solving problems. Most colleges consider fluency in algebra to be a vital prerequisite to a college-level liberal arts curriculum.
Sound intimidating? It’s not.
If you take the time to master the four core skills presented in these 13 lessons, you will gain the knowledge and practice you need to master even the toughest SAT Math “Heart of Algebra” questions.
Skill 1: Working with Expressions
Lesson 1: Using algebraic expressions
To solve tough SAT math problems, you must be fluent in defining, manipulating, and analyzing algebraic expressions.
Corrine drives to her office at an average speed of 50 miles per hour. When she returns home by the same route, the traffic is lighter and she averages 60 miles per hour. If her trip home is 10 minutes shorter than her trip to her office, what is the distance, in miles, from Corrine’s home to her office?
(Medium-hard) Why does everyone hate “word problems” like this one? For most of us, the problem is that the equations aren’t “set up” for us—we have to set them up ourselves, which can be a pain in the neck. But we can make these problems much easier by breaking them down into clear steps.
Step 1. Identify: In this problem, there are six relevant quantities:
• the speed from home to work
• the distance from home to work
• the time it takes to get from home to work
• the speed from work to home
• the distance from work to home
• the time it takes to get from work to home
This may seem like a lot, but as we will see, keeping track of them is quite manageable.
Step 2. Express: The problem gives us enough information to express all six quantities in terms of only two “unknowns.” If d is the distance, in miles, from her home to her office, and t is the time, in hours, it takes her to get home from the office, then we can express our six quantities, respectively, as
Step 3. Translate: To translate the facts of this problem into equations, we must know the formula distance = average speed × time. Applying this to each trip gives us
Step 4. Analyze and Solve: We have now reduced the problem to a “two by two system,” that is, two equations with two unknowns. Since the number of equations equals the number of unknowns, we should be able to solve for those unknowns. (In Lessons 12 and 13, we will review these concepts and techniques.) Since the unknown d is isolated in both equations, substitution is simple:
Since t represents the time it took Corrine to return home, in hours, this means it took her 5/6 hours (or 50 minutes) to get from her office to her home, and 5/6 hour + 1/6 hour = 1 hour to get to her office from home. But remember, the question asks for the distance from her home to her office, which we can find by substituting into either of our equations:
50(5/6 + 1/6) or 60(5/6) = 50 miles
Lesson 2: The Laws of Arithmetic
When expressing or simplifying a quantity, you frequently have many options. For instance, the expression 4x2 – 12x can also be expressed as 4x(x – 3). Similarly, 3.2 can be expressed as 16/5 or 3⅕ or 32/10. Which way is better? It depends on what you want to do with the expression. Different forms of an expression can reveal different characteristics of that quantity or the equation in which it appears. To gain fluency in expressing quantities, you must understand the Laws of Arithmetic.
To simplify complex expressions, you must know the Order of Operations:
PG-ER-MD-AS
Step 1: PG (parentheses and other grouping symbols, from innermost to outermost and left to right)
Since this expression contains no parentheses, we don’t have to worry about “grouped” operations, right? Wrong! Remember that fraction bars and radicals are “grouping symbols” just like parentheses are.
In other words, we can think of this expression as
If a set of parentheses contains only one operation, then we simply do that operation:
If it contains more than one operation, then we must move on to the next step.
Step 2: ER (exponents and roots, from innermost to outermost and left to right)
Do any of the parentheses contain exponents or roots? Yes, so we must perform that operation next:
Step 3: MD (multiplication and division, from left to right)
Next, we do any multiplication inside the parentheses:
Step 4: AS (addition and subtraction, from left to right)
Now we do any addition and subtraction left in the parentheses:
Once all the “grouped” operations are completed, we run through the order of operations once again to finish up. Exponents or roots? No. Multiplication or division? Yes:
1.875 + 2
Addition or subtraction? Yes: 1.875 + 2 = 3.875
What is the sum of the first 100 positive integers?
(Hard) Here, following the order of operations would be, shall we say, less than convenient: it would require 99 computations. Even with a calculator, it would be a pain. But here is a much simpler method:
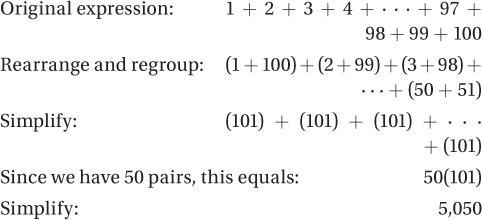
This gives us exactly the same result as the order of operations would give, but with just a few simple calculations. How did we do it? By using three more laws of arithmetic: the commutative law of addition, the associative law of addition, and the distributive law of multiplication over addition.
Which of the following is equivalent to 3(34 × 53)? [No calculator]
A) 3(34) × 3(53)
B) 94 + 153
C) 94 × 153
D) 35 × 53
Before making your choice, check the laws of arithmetic; don’t make up your own laws. Which laws of arithmetic can we use? Since the expression is a product, we can use the commutative law of multiplication and jumble up the terms, or the associative law of multiplication and regroup the terms any way we want (or not at all). Using the associative law gives us
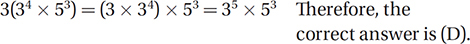
If x ≠ 0, which of the following equals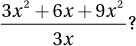 
A)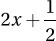 
B)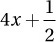 
C) 2x2 + 2
D) 4x + 2
So the correct answer is (D). Look at each step carefully and notice how each one uses a particular Law of Arithmetic. In particular, notice that the “combining of like terms” in steps 1–3 is really an example of commuting, associating, and (un)distributing. Even more interesting, notice that steps 4–5 show that division distributes just like multiplication does.
You can also distribute division over addition just as you can distribute multiplication.
How many distinct values of x are solutions to the equation x2 + 4 = –4x ?
A) none
B) one
C) two
D) three
(Medium) You might recognize that this equation is a quadratic equation (which we will discuss in much more detail in Chapter 9) and remember that such equations usually have two distinct solutions, but not always, so we must look at this equation more carefully.
Step 2 might seem a bit mysterious. Why did we write 4x as 2x + 2x? Here we are using the Product-Sum Method for factoring quadratics, which is explained in a bit more detail in Chapter 9, Lesson 4. For now, though, just notice that each step follows a particular Law of Arithmetic.
If the product of two numbers is 0, then one of those numbers must be 0. (This is the Zero Product Property.) Therefore x + 2 = 0 and so x = –2. Since the other factor is the same, we only get one solution to this equation, and the answer is (B).
To check the equation in step 5, we can FOIL the product of binomials on the left side to make sure we get the same expression we had back in step 1: (x + 2)(x + 2) = x2 + 4x + 4, which is precisely the expression we started with in step 1, confirming that our work is correct.
This means that the factoring process in steps 2–5 can be thought of as un-FOILing. We will look at this method of factoring more carefully in Chapter 9.
Make sure you know how to FOIL and un-FOIL.
FOILing is simply the shortcut for multiplying two binomials, which requires applying the distributive law twice. For example:
Exercise Set 1 (No Calculator)
(1 – (1 – (1 – 2))) – (1 – (1 – (1 – 3))) =
When 14 is subtracted from 6 times a number, 40 is left. What is half the number?
Four consecutive even numbers have a sum of 76. What is the greatest of these numbers?
If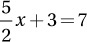 
, then 10x + 12 =
What number decreased by 7 equals the opposite of five times the number?
If 5d + 12 = 24, then 5d – 12 =
If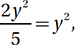 
then y + 5 =
The product of x and y is 36. If both x and y are integers, then what is the least possible value of x – y ?
A) –37
B) –36
C) –35
D) –9
If a factory can manufacture b computer screens in n days at a cost of c dollars per screen, then which of the following represents the total cost, in dollars, of the computer screens that can be manufactured, at that rate, in m days?
A)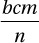 
B)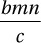 
C)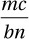 
D)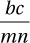 
Which of the following is equivalent to 5x(2x × 3) – 5x2 for all real values of x ?
A) 5x2 + 15x
B) 25x2
C) 5x2 – 15x
D) 10x2 × 15x – 5x2
The symbol O represents one of the fundamental operators: +, –, ×, or ÷. If (x O y) × (y O x) = 1 for all positive values of x and y, then O can represent
A) +
B) ×
C) –
D) ÷
Exercise Set 1 (Calculator)
The difference of two numbers is 4 and their sum is 14. What is their product?
If x + y – 1 = 1 – (1 – x), what is the value of y ?
If 3x2 + 2x = 40, then 15x2 + 10x =
Ellen is currently twice as old as Maria, but in 6 years, Maria will be 2/3 as old as Ellen. How old is Ellen now?
If 2x – 2y = 5 and x + y = 6, what is the value of x2 – y2 ?
On a typical day, a restaurant sells n grilled cheese sandwiches for p dollars each. Today, however, the manager reduced the price of grilled cheese sandwiches by 30% and as a result sold 50% more of them than usual. Which of the following represents the revenue for today’s grilled cheese sandwich sales, in dollars?
A) 0.5np – 0.3
B) 1.05np
C) 1.20np
D) 1.50np
For all real numbers x and y, 4x(x) – 3xy(2x) =
A) 12x2y(x – 2y)
B) 2x2(2 – 3y)
C) 2x2(2 + 3y)
D) 4xy(x – 3y)
If a = 60(99)99 + 30(99)99, b = 99100, and c = 90(90)99, then which of the following expresses the correct ordering of a, b, and c ?
A) c < b < a
B) b < c < a
C) a < b < c
D) c < a < b
Which of the following statements must be true for all values of x, y, and z ?
I (x + y) + z = (z + y) + x
II (x – y) – z = (z – y) – x
III (x ÷ y) ÷ z = (z ÷ y) ÷ x
A) I only
B) I and II only
C) I and III only
D) II and III only
Carlos began with twice as much money as David had. After Carlos gave $12 to David, Carlos still had $10 more than David. How much money did they have combined at the start?
A) $34
B) $68
C) $102
D) 108
EXERCISE SET 1 ANSWER KEY
No Calculator
Calculator
Lesson 3: Simplifying expressions and operations
If x and y are positive numbers and 3x - 2y = 7, what is the value of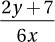 
?
A) 
B) 
C) 
D) 
(Easy) Working with algebraic equations doesn’t always mean “solving for x.” Notice that this particular question doesn’t ask for the values of x or y, but rather for the value of a more complicated expression. This may seem harder, but it’s actually pretty simple if you understand the Law of Substitution.
How does this help us here? Notice that if we simply add 2y to both sides of the equation, we get
Therefore, by the Law of Substitution, we can substitute 3x for 2y + 7 or vice-versa. Since 2y + 7 appears in the expression we are asked to evaluate, it makes sense to replace it with 3x:
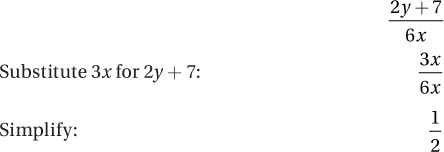
Increasing a positive number x by 25% and then decreasing the result by 50% is equivalent to dividing x by what number?
A) 1.333
B) 1.5
C) 1.6
D) 1.625
(Medium) Increasing a quantity by 25% is equivalent to multiplying it by 1.25, because the final amount is 125% of the original amount (Chapter 8, Lesson 8). Decreasing a quantity by 50% is equivalent to multiplying it by .5, because the final amount is 50% of the original amount. Therefore, performing both changes is equivalent to multiplying by 1.25 × 0.50, or 0.625, which is equal to 5/8. But the question asks us for the equivalent division. Here, we need to remember a simple rule: multiplying by a number is equivalent to dividing by its reciprocal. Therefore, multiplying by 5/8 is the same as dividing by 8/5, which is 1.6. Therefore, the correct answer is (C).
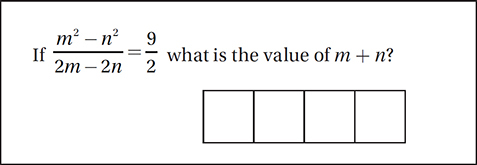
(Easy) When a problem includes a complicated expression, we should try to simplify it, but always keep an eye on what the question is asking. In this case, simplifying to find the value of m + n requires knowing some factoring identities.
Lesson 4: Using conversion as a problem-solving tool
Niko is 27 inches shorter than his father, who is 5 feet 10 inches tall. How tall is Niko? (1 foot = 12 inches)
A) 3 feet 4 inches
B) 3 feet 6 inches
C) 3 feet 7 inches
D) 3 feet 10 inches
(Easy) Solving this problem requires unit conversions. To convert inches to feet, we multiply by the conversion factor (1 foot/12 inches). To convert feet to inches, we multiply by its reciprocal (12 inches/1 foot). If Niko’s father is 5 feet 10 inches tall, he is 5 feet × (12 inches/1 foot) + 10 inches = 70 inches tall. If Niko is 27 inches shorter, he is 70 – 27 = 43 inches tall, which is equivalent to 43 inches × (1 foot/12 inches) = 3 7/12 feet, or 3 feet 7 inches, so the correct answer is (C).
If a factory can manufacture b computer screens in n days at a cost of c dollars per screen, then which of the following represents the total cost, in dollars, of the computer screens that can be manufactured, at that rate, in m days?
A)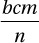
B)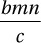
C)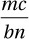
D)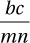
(Medium) This problem, from the previous exercise set, can be solved in several different ways. One method is to simply choose values for the unknowns and turn the problem into an arithmetic problem instead of an algebra problem. But here we will look at it as a conversion problem.
We can think of this problem as being a “conversion” from a quantity of days to an equivalent quantity of dollars. We are given that this factory is working for m days, so we write this quantity down, including the units, and we multiply by the conversion factors until we get dollars:
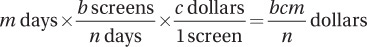
So the correct answer is (A).
Exercise Set 2 (No Calculator)
If bag A weighs 4 pounds 5 ounces and bag B weighs 6 pounds 2 ounces, how much heavier, in ounces, is bag B than bag A? (1 pound = 16 ounces)
If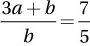 
, what is the value of 
?
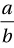If x – 2y = 10 and x ≠ 0, what is the value of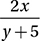 
If a – b = 4 and a2 – b2 = 3, what is the value of a + b ?
If 6 gricks are equivalent to 5 merts, then 2 merts are equivalent to how many gricks?
If the function {x} is defined by the equation {x} = (1 – x)2, what is the value of {{4}} ?
If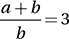 
and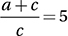 
, what is the value of 
(x – 9)(x – a) = x2 – 4ax + b
In the equation above, a and b are constants. If the equation is true for all values of x, what is the value of b ?
A) –27
B) –12
C) 12
D) 27
If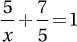 
, what is the value of x ?
A)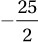 
B) –7
C)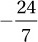 
D)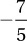 
(p + 2)2 = (p – 5)2
The equation above is true for which of the following values of p ?
A) –2 and 5
B) 2 and –5
C) 1.5 only
D) 5 only
If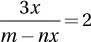 
for all positive values of m and n, then
which of the following is equal to x ?
A)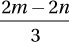 
B)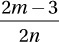 
C)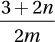 
D)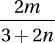 
Exercise Set 2 (Calculator)
Let m be a positive real number. Increasing m by 60% then decreasing the result by 50% is equivalent to dividing m by what number?
What is the sum of the first 50 positive even integers?
Three years ago, Nora was half as old as Mary is now. If Mary is four years older than Nora, how old is Mary now?
If 2/3 of the seats at a football stadium were filled at the beginning of the game, and at halftime 1,000 spectators left, leaving 3/7 of the seats filled, what is the total number of seats in the stadium?
If three candy bars and two gumdrops cost $2.20, and four candy bars and two gumdrops cost $2.80, what is the cost, in dollars, of one gumdrop?
If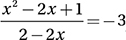 
, what is the value of x –1 ?
Subtracting 3 from a number and then multiplying this result by 4 is equivalent to multiplying the original number by 4 and then subtracting what number?
In a poker game, a blue chip is worth 2 dollars more than a red chip, and a red chip is worth 2 dollars more than a green chip. If 5 green chips are worth m dollars, then which of the following represents the value, in dollars, of 10 blue chips and 5 red chips?
A) 50 + 3m
B) 18 + 60m
C) 40 + 3m
D) 28 + 20m
A train travels at an average speed of 50 miles per hour for the first 100 miles of a 200-mile trip, and at an average of 75 miles per hour for final 100 miles. What is the train’s average speed for the entire trip?
A) 58.5 mph
B) 60.0 mph
C) 62.5 mph
D) 63.5 mph
Which of the following is equivalent to 3m(m2 × 2m) for all real values of m ?
A) 3m2 + 6m
B) 3m2 × 6m
C) 3m3 × 6m2
D) 6m4
If the cost of living in a certain city increased by 20% in the 10 years from 1980 to 1990, and increased by 50% in the 20 years from 1980 to 2000, what was the percent increase in the cost of living from 1990 to 2000?
A) 15%
B) 20%
C) 25%
D) 30%
EXERCISE SET 2 ANSWER KEY
No Calculator
Calculator
Skill 2: Working with Linear Equations
Lesson 5: Constructing and interpreting linear equations
The Horizon Resort charges $150 per night for a single room, and a one-time valet parking fee of $35. There is a 6.5% state tax on the room charges, but no tax on the valet parking fee. Which of the following equations represents the total charges in dollars, c, for a single room, valet parking, and taxes, for a stay of n nights at The Horizon Resort?
A) c = (150 + 0.065n) + 35
B) c = 1.065(150n) + 35
C) c = 1.065(150n + 35)
D) c = 1.065(150 + 35)n
(Medium) This question asks us explicitly to set up an equation to express a mathematical relationship in a word problem. Usually, this is just the first step in analyzing the situation more deeply, for instance, finding particular values of the variables that satisfy certain conditions, or interpreting the meanings of terms or coefficients in the equation, but this problem only asks us to set up the equation.
When translating verbal information into an equation, it’s helpful to take small steps. First, since the room charge is $150 per night, the charge for n nights is $150n. If a 6.5% tax is added to this, the room charge becomes 150n + 0.065(150n) = 1.065(150n). The $35 valet parking charge is added separately, and not taxed, so the total charges are 1.065(150n) + 35, and the correct answer is (B). Notice that this equation shows a linear relationship between c and n.
Which of the following represents the equation of the line with an x-intercept of 6 that passes through the point (4, 4)?
A)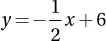 
B) y = 2x – 4
C) y = –2x + 12
D) y = –2x + 6
(Easy) This question asks you to construct the equation of a line given some facts about its graph. Start by drawing a graph (on the xy-plane) of the given information in the space next to the question. It also helps to know something about the different forms of linear equations and what they reveal about the graph of the line.
Graph of a line in the xy-plane
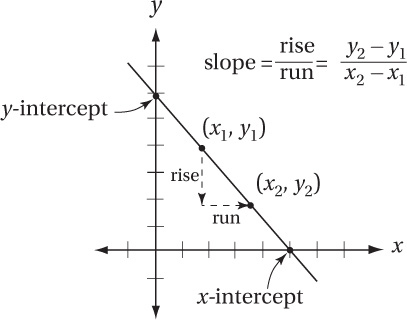
Forms of linear equations
In this problem, we are given two points on the line: (4, 4) and the x-intercept (6, 0). We can calculate the slope using the slope formula above: slope = (4 – 0)/(4 – 6) = (4)/(–2) = –2. If we use this slope and the point (6, 0), we can set up the equation in point-slope form:
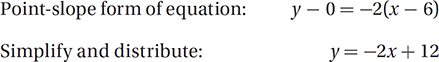
This is the equation in (C). Notice that this equation is in slope-intercept form, and reveals that this line also has a y-intercept of 12. Check this fact against your diagram, and also check that both given points, (4, 4) and (6, 0), satisfy this equation.
Lesson 6: Solving equations with the Laws of Equality
(Medium) At first glance, this doesn’t look like a linear equation. But one simple move reveals that it is:
As this shows, sometimes solving equations requires a clever use of the Laws of Equality.
If x2 = y2, then which of the following must be true?
I x = y
II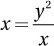 
III x = |y|
A) none
B) I only
C) I and II only
D) I, II and III
(Medium-hard) This question tests your skills of deductive logic. Notice it is not asking which statements can be true, but rather which must be true. It seems that if we “unsquare” both sides of the original equation, we get the equation in I. If we divide the original equation by x on both sides, we get the equation in II. Does this mean that statements I and II are necessarily true? No, because we violated rule 3 in both cases. If x2 = y2, it does not follow that x = y. Notice that x could be 2 and y could be –2. These values certainly satisfy the original equation, but they do not satisfy the equations in I or III. They do, however, satisfy the equation in II, because 2 = (–2)2/2. However, statement II is still not necessarily true. What if x and y were both 0? This would satisfy the original equation, but 0 ≠ (0)2/(0) because 0/0 is undefined. Therefore, the correct answer is (A).
Lesson 7: Making and analyzing graphs of linear equations
If m is a constant greater than 1, which of the following could be the graph in the xy-plane of x + my + m = 0 ?
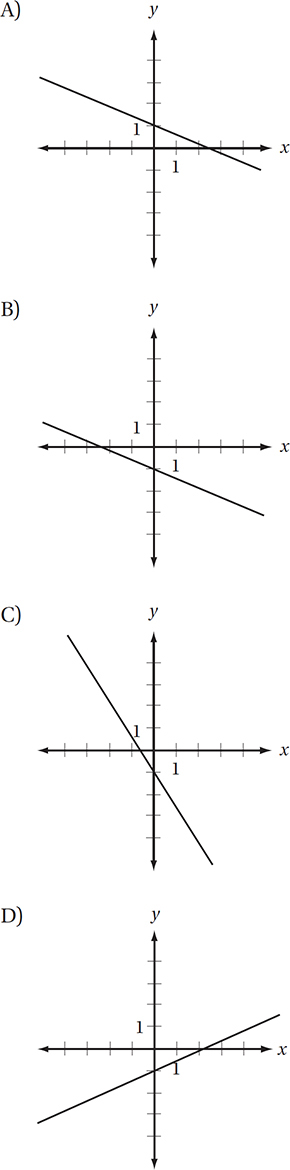
(Medium-hard) First, we should try to get the equation into a more useful form. Let’s try the slope-intercept (y = mx + b) form:
This shows that the line has a slope of –1/m and a y-intercept of –1. Since the problem tells us that m is greater than 1, we know that the slope (–1/m) must be between –1 and 0. The only graph that satisfies these conditions is (B).
The points A(10, 4) and B(–2, k) are 13 units apart. Which of the following equations could describe the line that contains points A and B ?
A) 13x + 12y = 178
B) 5x + 12y = 98
C) 5x + 12y = 98
D) 5x + 13y = –2
(Hard) Drawing a diagram will help us analyze this problem. Although we don’t know precisely where point B is, we know it is somewhere on the line x = –2. This gives us the following picture:
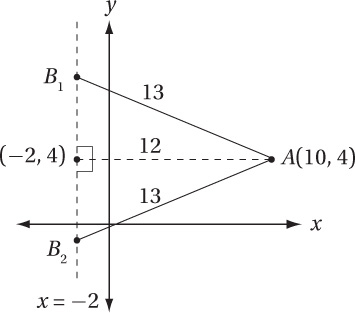
Next, notice that all of the equations given in the choices are in “standard” form, and in standard form the slope of the line is –a/b. Therefore, the slopes of these lines are, respectively, (A) –13/12, (B) –5/12, (C) 5/12, and (D) 5/13. Therefore, finding the slope of the line should help us choose the correct equation. Looking at the diagram more closely, notice that it includes two right triangles, and we can find the missing side of each one using the Pythagorean Theorem, or just by noticing that they are both 5-12-13 right triangles (52 + 122 = 132). Putting this information into the diagram shows us that B can therefore be at (–2, 9) or (–2, –1).
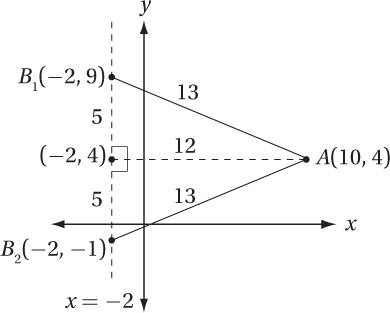
Therefore, the slope (rise/run) of the line containing B1 is –5/12, and the slope of the line containing B2 is 5/12. This means that our answer is either (B) or (C). How do we choose between them? Just remember that the line must contain the point (10, 4). If you plug x = 10 and y = 4 into these equations, only (B) works: 5(10) + 4(12) = 98.
Exercise Set 3 (No Calculator)
If x – 2(1 – x) = 5, what is the value of x ?
If f(x) = –2x + 8, and f(k) = –10, what is the value of k ?
What is the slope of the line that contains the points (–2, 3) and (4, 5) ?
What is the slope of the line described by the equation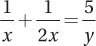 
?
Line l is perpendicular to the line described by the equation 5x + 11y = 16. What is the slope of line l ?
If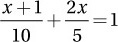 
, what is the value of x ?
What is the y-intercept of the line containing the points (3, 7) and (6, 3) ?
In the xy-plane, the graph of y = h(x) is a line with slope –2. If h(3) = 1 and h(b) = –9, what is the value of b ?
If a train maintains a constant speed of 60 miles per hour, it can travel 4 miles per gallon of diesel fuel. If this train begins a trip with a full 200 gallon tank of diesel fuel, and maintains a speed of 60 miles per hour, which of the following equations represents the number of gallons, g, left in the tank t hours into the trip?
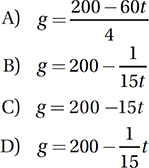
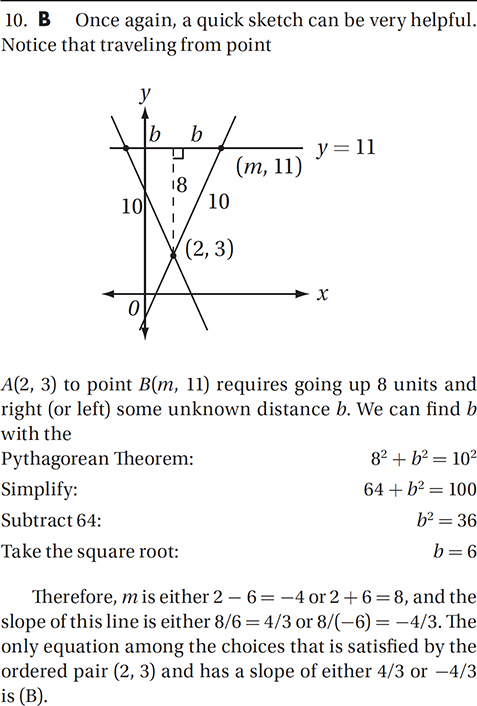
The points A(2, 3) and B(m, 11), are 10 units apart. Which of the following equations could describe the line that contains points A and B ?
A) 8x + 6y = 11
B) 8x – 6y = –2
C) 6x + 8y = 36
D) 6x – 8y = –12
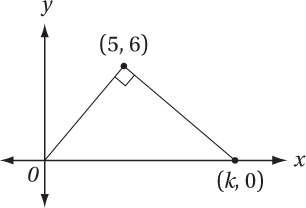
The figure above shows a right triangle with vertices at the origin, (5, 6) and (k, 0). What is the value of k ?
Exercise Set 3 (Calculator)
If the points (2, 4), (5, k), and (8, 20) are on the same line, what is the value of k ?
Line l has a slope of 3 and a y-intercept of –4. What is its x-intercept?
If f(–1) = 1 and f(3) = 2 and f is a linear function, what is the slope of the graph y = f(x) ?
If f(–1) = 1 and f(3) = 2 and f is a linear function, what is f(5) ?
In the xy-plane, the graph of line n has an x-intercept of 2b and an y-intercept of –8b, where b ≠ 0. What is the slope of line n ?
If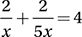 
, what is the value of x ?
If the line 3x – 2y = 12 is graphed in the xy-plane, what is its x-intercept?
If the graphs of the equations 5x – 2y = 5 and 6x + ky = 9 are perpendicular, what is the value of k ?
The net profit for the sales of a product is equal to the total revenue from the sales of that product minus the total cost for the sales of that product. If a particular model of calculator sells for $98, and the cost for making and selling n of these calculators is $(35n + 120,000), which of the following equations expresses the net profit in dollars, P, for making and selling n of these calculators?
A) P = 63n – 120,000
B) P = 63n + 120,000
C) P = 63(n – 120,000)
D) P = 63(n + 120,000)
Which of the following represents the equation of the line with an x-intercept of 5 and a y-intercept of 6 ?
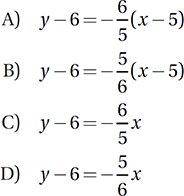
The table above shows several ordered pairs corresponding to the linear function f. What is the value of a + b ?
A) 12
B) 16
C) 20
D) It cannot be determined from the information given.
EXERCISE SET 3 ANSWER KEY
Part 1: No Calculator
Part 2: No Calculator
Skill 3: Working with Inequalities and Absolute Values
Lesson 8: Understanding inequalities and absolute values
On the real number line, a number, b, is more than twice as far from –3 as it is from 3. Which of the following equations can be solved to find all possible values of b ?
A) |b - 3| > 2|b + 3|
B) |b + 3| > 2|b - 3|
C) 2|b - 3| > |b + 3|
D) 2|b + 3| > |b - 3|
(Medium-hard) We can use this definition to translate the problem. The key is to translate the statement “b is more than twice as far from –3 as it is from 3” into a statement about distances: “The distance between b and –3 is more than twice the distance between b and 3.” Notice how easily this translates into an inequality:
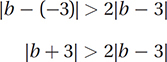
which is choice (B).
The label on each box of Deer Valley Raisins says that it contains 1.25 pounds of raisins, but industry standards allow these boxes to be sold with anywhere from 1.20 pounds to 1.32 pounds of raisins. If x represents the number of pounds of raisins in a box of Deer Valley raisins that meets industry standards, which of the following inequalities represents all possible values of x ?
A) |x – 1.25| ≤ 0.05
B) |x – 1.26| ≤ 0.06
C) |x – 1.25| ≤ 0.06
D) |x – 1.26| ≤ 0.05
(Medium-hard) The important fact here is the industry standard, not the label on the box. The standard says that the box can contain any weight of raisins between 1.20 pounds and 1.32 pounds. The midpoint of this range is (1.20 + 1.32)/2 = 1.26 pounds of raisins, and this midpoint is 0.06 from the endpoints of that range (1.32 – 1.26 = 0.06 and 1.26 – 1.20 = 0.06). Therefore, x can be any value that is 0.06 or less away from 1.26. Since the expression for the distance from x to 1.26 is |x – 1.26|, the correct inequality is |x – 1.26| ≤ 0.06, which is choice (B).
Lesson 9: Solving inequalities with the Laws of Inequality
If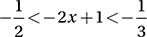 
, what is one possible value of x?
(Easy) This kind of inequality is called a “sandwich inequality” because the expression in the middle is between the other two, like meat between slices of bread. Working with inequalities like this one requires understanding the Laws of Inequality.
The Laws of Inequality
Every inequality is a “tipped” scale, and the Laws of Inequality are simply the rules for “keeping the scale tipped the right way,” that is, deducing other true inequalities that follow from the original one. In a nutshell, the Laws of Inequality say that
1. You may make changes to any inequality, as long as you follow rules 2, 3 and 4.
2. Whatever you do to one side of the inequality, you must do to the other.
3. You may not perform undefined operations (like dividing by 0), or operations that have more than one possible result (like taking a square root).
4. If you multiply or divide both sides by a negative number, you must “switch” the direction of the inequality. This is because multiplying or dividing by a negative number involves a reflection over the origin on the number line, and this reflection requires the “switch”:
So we can solve the sandwich inequality by applying
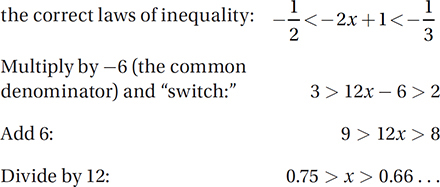
Therefore, any value greater than 0.666 but less than 0.750 is correct.
Which of the following must be true if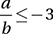 
A) a ≤ –3b
B) a ≥ –3b
C) a ≤ –3b < 0 and a ≥ –3b > 0
D) a ≤ –3b < 0 or a ≥ –3b > 0
(Hard) We might be tempted to multiply both sides of the inequality by b and get the inequality in (A). But this would be incorrect because it would ignore rule 4. We need to consider the possibility that b might be negative. Let’s think about possible solutions to the original inequality. Notice that a = 10 and b = –2 gives a possible solution, because 10/(–2) = –5 ≤ –3. But this would not satisfy the inequality in (A): 10 is not less than or equal to (–3)(–2) = 6.
To solve this inequality, we will need to consider two distinct possible conditions:
Condition 1: If b > 0, then a ≤ –3b and therefore a ≤ –3b < 0
Condition 2: If b < 0, then a ≥ –3b and therefore a ≥ –3b > 0
which is the answer in choice (D).
Lesson 10: Graphing inequalities
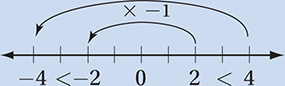
On the real number line, a number, b, is more than twice as far from –3 as it is from 3. Which of the following graphs represents all possible values of b ?
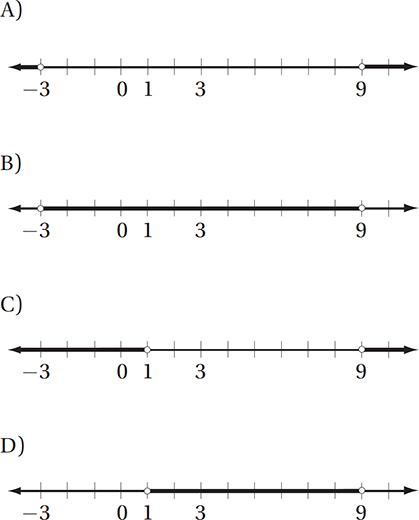
(Medium) We saw this scenario in Lesson 8, but now we are asked to graph the solution. Recall from Lesson 8 that this relationship is expressed by the inequality |b + 3| > 2|b – 3|. How do we translate this into a graph? The simplest way to start is to visualize the number line, and to think about a related, but simpler, question: What if b is exactly twice as far from –3 as it is from 3? A little guessing and checking should reveal that two points work:
Notice that 9 works because 3 is the midpoint between –3 and 9, and 1 works because it is 2/3 of the way from –3 to 3. Also, you can confirm that both numbers satisfy the equation |b + 3| = 2|b – 3|. These two points now divide the line into three parts: everything less than 1, everything between 1 and 9, and everything greater than 9. A little bit of checking (just pick a number from each portion and plug it into our inequality) confirms that only the numbers in the middle portion satisfy our inequality, so the correct graph is the one in choice (D).
Exercise Set 4 (No Calculator)
What positive number is twice as far from 10 as it is from 1 ?
If the points (2, a) and (14, b) are 20 units apart, what is |a – b| ?
What is the least integer n for which 
If |x + 4| = |x – 5|, what is the value of x ?
What is the greatest integer value of n such that 
What is the only integer b for which 
and 3b ≥ 7.5 ?
If (b + 2)2 = (b – 5)2, what is the value of b ?
Which of the following statements is equivalent to the statement –4< 2x ≤ 2 ?
A) x > –2 and x ≤ 1
B) x < –2 or x ≥ 1
C) x ≥ –2 and x < 1
D) x ≤ –2 or x > 1
The annual profit from the sales of an item is equal to the annual revenue minus the annual cost for that item. The revenue from that item is equal to the number of units sold times the price per unit. If n units of a portable heart monitor were sold in 2012 at a price of $65 each, and the annual cost to produce n units was $(20,000 + 10n), then which of the following statements indicates that the total profit for this heart monitor in 2012 was greater than $500,000?
A) 500,000 < 55n – 20,000
B) 500,000 > 55n – 20,000
C) 500,000 < 55n + 20,000n
D) 500,000 < 75n – 20,000n
Colin can read a maximum of 25 pages an hour. If he has been reading a 250 page book for h hours, where h < 10, and has p pages left to read, which of the following expresses the relationship between p and h ?
A)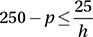 
B)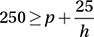 
C) 250 – p ≤ 25h
D) 250 + 25h ≤ p
On the real number line, a number, x, is more than 4 times as far from 10 as it is from 40. Which of the following statements describes all possible values of x ?
A) x < 34 or x > 50
B) x > 40
C) 34 < x < 50
D) 32.5 < x < 160
Exercise Set 4 (Calculator)
If a < 0 and |a – 5| = 7, what is |a| ?
If n is a positive integer and 16< |6 – 3n|< 19, what is the value of n ?
What is the only integer n such that 20 – 2n > 5 and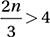 
What is the smallest number that is as far from 9.25 as 3 is from –1.5 ?
If |2x + 1| = 2|k – x|, for all values of x, what is the value of |k| ?
Which of the following is equivalent to the statement |x – 2|< 1 ?
A) x < 3
B) x < –1
C) 1 < x < 3
D) –1 < x < 3
If the average (arithmetic mean) of a and b is greater than the average (arithmetic mean) of c and 2b, which of the following must be true?
A) b > 0
B) a > b
C) a > b + c
D) a + c > b
Of the statements below, which is equivalent to the statement “The distance from x to 1 is greater than the distance from x to 3 ?
A) 1 < x < 3
B) x > 2
C) x < 2
D) x – 1 > 3
Which of the following is equivalent to the statement 4x2 ≥ 9 ?
A) 2x > 3
B) x ≥ 1.5 or x ≤ –1.5
C) |x| > 2
D) –1.5 ≤ x ≤ 1.5
The graph above indicates the complete solution set to which of the following statements?
A) |x – 3| > 3
B) |x| < 6
C) |x – 6| < 6
D) |x – 3| < 3
Which of the following is true for all real values of x ?
A) |x| > 0
B) x < 2 or x > 1
C) x > –2 or x < –3
D) x2 – 1 > 0
EXERCISE SET 4 ANSWER KEY
No Calculator
Calculator
Skill 4: Working with Linear Systems
Lesson 11: Constructing, graphing, and interpreting linear systems
Two high school teachers took their classes on a field trip to a museum. One class spent $154 for admission for 20 students and 3 adults, and the other class spent $188 for admission for 24 students and 4 adults. Which of the following systems of equations could be solved to determine the price of a single student admission, s, and the price of a single adult admission, a, in dollars?
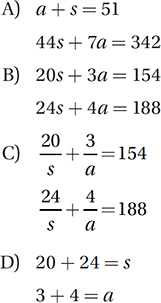
(Medium) This problem can be described with a two-by-two system of equations, that is, two equations with two unknowns. The two equations come from two facts: one class spent $154 for admission and the other class spent $188 for admission. The cost of 20 student admissions and 3 adult admissions is 20s + 3a, so the first equation is 20s + 3a = 154. Similarly, the equation for the other class is 24s + 4a = 188, so the correct answer is (B).
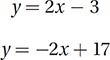
If the solutions to the two equations above are graphed in the xy-plane, what is the y-coordinate of the point at which the graphs intersect?
(Easy) Since the equations of both lines are given in slope-intercept form, we could graph the two lines in the xy-plane to find their point of intersection.
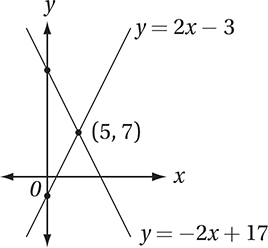
Therefore, the point (5, 7) gives us the only solution to this system, and so the answer to the original question is 7.
Alternately, (as we will see in Lesson 13) we can just add the corresponding sides of the two equations together to get 2y = 14, which yields y = 7.
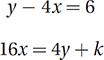
For what value of k does the system of equations above have at least one solution?
A) –32
B) –30
C) –24
D) –20
(Medium) This is a two-by-two system of linear equations, and so its solution is the intersection of those two lines. If we convert them to slope-intercept form, we get y = 4x + 6 and y = 4x – k/4, which reveals that these two lines have the same slope. This means that they are either parallel lines or identical lines. Two lines with the same slope can intersect only if they are the same line, and therefore –k/4 = 6 and k = –24.
Lesson 12: Solving systems by substitution
Let’s go back to the second linear system from Lesson 11. This system can also be solved with a simple application of the Law of Substitution.
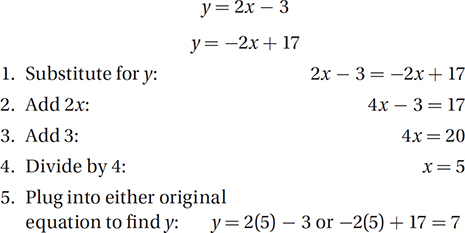
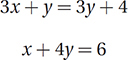
Based on the system of equations above what is the value of xy ?
(Medium) This system is not quite as tidy as the previous one, but we can still solve it by using the Law of Substitution.
Lesson 13: Solving systems by linear combination
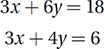
Based on the system of equations above, what is the value of y ?
(Easy) Although this system can be solved by substitution (try it as an exercise), the setup of these equations suggests a much easier method, known as linear combination. It’s based on a simple idea:
If we apply this rule to our system, notice that we can easily eliminate x from the system by just subtracting the equations:
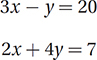
Based on the system of equations above, what is the value of x – 5y ?
(Medium) This question looks tougher than the previous one, because it’s not just asking for x or y. It seems that the question requires us to solve the system for x and y and then to plug these values into the expression x – 5y and evaluate. We could do that, but there is a much simpler method. Notice that a simple combination gives us the expression the question is asking for.
Exercise Set 5 (No Calculator)
If 3x + 2y = 72, and y = 3x, what is the value of x ?
If 2a – 7b = 10 and 2a + 7b = 2, what is the value of 4a2 – 49b2 ?
If the lines y = –4x – 3 and y = –3x – b intersect at the point (–1, c), what is the value of b ?
If the lines 4x + 5y = 13 and 4y + kx = 2 are parallel, what is the value of k ?
If the lines 4x + 5y = 13 and 6y – kx = 6 are perpendicular, what is the value of k ?
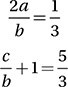
Based on the system of equations above, what is the value of 
?
If ab = –4 and abc = 12, what is the value of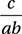 
?
If a and b are constants and the graphs of the lines 2x – 3y = 8 and ax + by = 2 are perpendicular, then what is the value of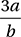 
?
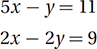
Based on the system of equations above, what is the value of 3x + y ?
A) –2
B) 0
C) 2
D) 4
Two numbers have a difference of 4 and a sum of –7. What is their product?
A) –33
B) –10.25
C) 8.25
D) 10.25
It costs Emma p dollars to make each of her custom bracelets, which she sells for m dollars apiece. She makes a profit of $60 if she makes and sells 5 of these bracelets, but she only makes a profit of $10 if she makes 5 bracelets but only sells 4 of them. How much does it cost Emma to make each bracelet?
A) $36
B) $38
C) $48
D) $50
Exercise Set 5 (Calculator)
If 2y = x + 1 and 4x + 6y = 0, then y =
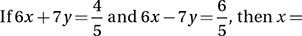
2x – 5y = 20
10x – 25y = 4k
For what value of k does the system of equations above have at least one solution?
At the beginning of the week, the ratio of cats to dogs at Glenna’s Pet Store was 4 to 5. By the end of the week, the number of cats had doubled, while the number of dogs had increased by 12. If the ratio of cats to dogs at the end of the week was 1 to 1, how many cats did the store have at the beginning of the week?
Jenny originally had twice as many friendship bracelets as Emilie. After Jenny gave Emilie 5 of her friendship bracelets, Jenny still had 10 more than Emilie. How many friendship bracelets did Jenny have originally?
The average (arithmetic mean) of x and y is 14. If the value of x is doubled and the value of y is tripled, the average (arithmetic mean) of the two numbers remains the same. What is the value of x ?
7m + 10n = 7
6m + 9n = 1
Based on the system of equations above, what is the value of 4m + 4n ?
In the xy-plane, perpendicular lines a and b intersect at the point (2, 2). If line a contains the point (7, 1), which of the following points is on line b ?
A) (0, 1)
B) (4, 5)
C) (7, 3)
D) (3, 7)
Which of the following pairs of equations has no solution in common?
A) 2x – 3y = 1 and 6x – 9y = 3
B) y = 4x and y = –4x
C) 2x – 3y = 1 and 6x – 9y = 2
D) y = 4x and 2y – 8x = 0
In the xy-plane, the line l is perpendicular to the line described by the equation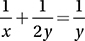 
. What is the slope of line l ?
A) –2
B)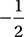 
C) 
D) 2
EXERCISE SET 5 ANSWER KEY
No Calculator
Calculator
