. At what rate is the radius expanding when the radius is 4 inches?This chapter deals with two different types of word problems that involve motion: related rates and the relationship between velocity and acceleration of a particle. The subject matter might seem arcane, but once you get the hang of them, you’ll see that these aren’t so hard, either. Besides, the AP exam tests only a few basic problem types.
The idea behind these problems is very simple. In a typical problem, you’ll be given an equation relating two or more variables. These variables will change with respect to time, and you’ll use derivatives to determine how the rates of change are related. (Hence the name: related rates.) Sounds easy, doesn’t it?
Example 1: A circular pool of water is expanding at the rate of . At what rate is the radius expanding when the radius is 4 inches?
Note: The pool is expanding in square inches per second. We’ve been given the rate that the area is changing, and we need to find the rate of change of the radius. What equation relates the area of a circle to its radius? A = πr2.
Step 1: Set up the equation and take the derivative of this equation with respect to t (time), and you’ll get this:
In this equation, 
represents the rate at which the area is changing, and 
is the rate at which the radius is changing. The simplest way to explain this is that whenever you have a variable in an equation (r, for example), the derivative with respect to time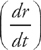 
represents the rate at which that variable is increasing or decreasing.
Step 2: Now we can plug in the values for the rate of change of the area and for the radius. (Never plug in the values until after you have taken the derivative or you will get nonsense!)
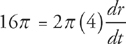
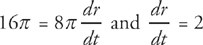
The radius is changing at a rate of 2 
. It’s important to note that this is the rate only when the radius is 4 inches. As the circle gets bigger and bigger, the radius will expand at a slower and slower rate.
Example 2: A 25-foot long ladder is leaning against a wall and sliding toward the floor. If the foot of the ladder is sliding away from the base of the wall at a rate of 15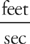 
, how fast is the top of the ladder sliding down the wall when the top of the ladder is 7 feet from the ground?
Here’s another classic related rates problem. As always, a picture is worth 1,000 words.
You can see that the ladder forms a right triangle with the wall. Let x stand for the distance from the foot of the ladder to the base of the wall, and let y represent the distance from the top of the ladder to the ground. What’s our favorite theorem that deals with right triangles? The Pythagorean theorem tells us here that x2 + y2 = 252. Now we have an equation that relates the variables to each other.
Now take the derivative of the equation with respect to t:
Just plug in what you know and solve. Since we’re looking for the rate at which the vertical distance is changing, we’re going to solve for 
.
Let’s see what we know. We’re given the rate at which the ladder is sliding away from the wall: 
= 15. The distance from the ladder to the top of the wall is 7 feet (y = 7). To find x, use the Pythagorean theorem. If we plug in y = 7 to the equation x2 + y2 = 252, x = 24.
Now plug all this information into the derivative equation:
Example 3: A spherical balloon is expanding at a rate of 
. How fast is the surface area of the balloon expanding when the radius of the balloon is 4 in?
Step 1: You’re given the rate at which the volume’s expanding, and you know the equation that relates volume to radius. But you have to relate radius to surface area as well, because you have to find the surface area’s rate of change. This means that you’ll need the equations for volume and surface area of a sphere:
You’re trying to find , but A is given in terms of r, so you have to get first. Because we know the volume, if we work with the equation that gives us volume in terms of radius, we can find . From there, work with the other equation to find . If we take the derivative of the equation with respect to t we get: 
. Plugging in for 
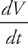and for r, we get: 60π = 4π(4)2 .
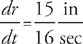
Step 2: Now, we take the derivative of the other equation with respect to t:
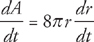
We can plug in for r and from the previous step and we get:
One final example.
Example 4: An underground conical tank, standing on its vertex, is being filled with water at the rate of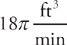 
. If the tank has a height of 30 feet and a radius of 15 feet, how fast is the water level rising when the water is 12 feet deep?
This “cone” problem is also typical. The key point to getting these right is knowing that the ratio of the height of a right circular cone to its radius is constant. By telling us that the height of the cone is 30 and the radius is 15, we know that at any level, the height of the water will be twice its radius, or h = 2r.
The volume of a cone is
. (You’ll learn
to derive this formula
through integration in
Chapter 17.)
You must find the rate at which the water is rising (the height is changing), or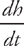 
. Therefore, you want to eliminate the radius from the volume. By substituting 
= r into the equation for volume, we get:
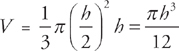
Differentiate both sides with respect to t:
Now we can plug in and solve for :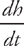
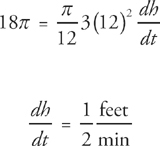
In order to solve related rates problems, you have to be good at determining relationships between variables. Once you figure that out, the rest is a piece of cake. Many of these problems involve geometric relationships, so review the formulas for the volumes and areas of cones, spheres, boxes, and other solids. Once you get the hang of setting up the problems, you’ll see that these problems follow the same predictable patterns. Look through these sample problems.
PROBLEM 1. A circle is increasing in area at the rate of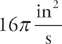 
. How fast is the radius increasing when the radius is 2 in?
Answer: Use the expression that relates the area of a circle to its radius: A = πr2
Next, take the derivative of the expression with respect to t:
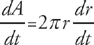
Now, plug in = 16π and r = 2
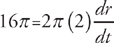
When you solve for , you’ll get 
.
PROBLEM 2. A rocket is rising vertically at a rate of 5,400 miles per hour. An observer on the ground is standing 20 miles from the rocket’s launch point. How fast (in radians per second) is the angle of elevation between the ground and the observer’s line of sight of the rocket increasing when the rocket is at an elevation of 40 miles?
Answer: First, draw a picture:
Now find the equation that relates the angle of elevation to the rocket’s altitude:
If we take the derivative of both sides of this expression with respect to t, we get:
We know that 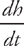= 5,400 miles per hour, but the problem asks for time in seconds, so we need to convert this number. There are 3,600 seconds in an hour, so 
miles per second. Next, we know that tan θ = 
, so when h = 40, tanθ = 2. Because 1 + tan2θ = sec2θ, we get sec2θ = 5.
Plug in this information:
Now try these problems on your own. The answers are in Chapter 23.
1. Oil spilled from a tanker spreads in a circle whose circumference increases at a rate of 40 ft/sec. How fast is the area of the spill increasing when the circumference of the circle is 100π ft?
2. A spherical balloon is inflating at a rate of 27π in3/sec. How fast is the radius of the balloon increasing when the radius is 3 in?
3. Cars A and B leave a town at the same time. Car A heads due south at a rate of 80 km/hr and car B heads due west at a rate of 60 km/hr. How fast is the distance between the cars increasing after three hours?
4. A cylindrical tank with a radius of 6 meters is filling with fluid at a rate of 108π m3/sec. How fast is the height increasing?
5. The sides of an equilateral triangle are increasing at the rate of 27 in/sec. How fast is the triangle’s area increasing when the sides of the triangle are each 18 inches long?
6. An inverted conical container has a diameter of 42 in and a depth of 15 in. If water is flowing out of the vertex of the container at a rate of 35π in3/sec, how fast is the depth of the water dropping when the height is 5 inches?
7. A boat is being pulled toward a dock by a rope attached to its bow through a pulley on the dock 7 feet above the bow. If the rope is hauled in at a rate of 4 ft/sec, how fast is the boat approaching the dock when 25 feet of rope is out?
8. A 6-foot-tall woman is walking at the rate of 4 ft/sec away from a street lamp that is 24 feet tall. How fast is the length of her shadow changing?
9. The voltage, V, in an electrical circuit is related to the current, I, and the resistance, R, by the equation V = IR. The current is decreasing at –4 amps/sec as the resistance increases at 20 ohms/sec. How fast is the voltage changing when the voltage is 100 volts and the current is 20 amps?
10. The minute hand of a clock is 6 inches long. Starting from noon, how fast is the area of the sector swept out by the minute hand increasing in in2/min at any instant?
Almost every AP exam has a question on position, velocity, or acceleration. It’s one of the traditional areas of physics where calculus comes in handy. Some of these problems require the use of integral calculus, which we won’t talk about until the second half of this book. So, this unit is divided in half; you’ll see the other half later.
If you have a function that gives you the position of an object (usually called a “particle”) at a specified time, then the derivative of that function with respect to time is the velocity of the object, and the second derivative is the acceleration. These are usually represented by the following:
Position: x(t) or sometimes s(t)
Velocity: v(t), which is x′(t)
Acceleration: a(t), which is x″(t) or v′(t)
By the way, speed is the absolute value of velocity.
Example 1: If the position of a particle at a time t is given by the equation x(t) = t3 − 11t2 + 24t, find the velocity and the acceleration of the particle at time t = 5.
First, take the derivative of x(t):
x′(t) = 3t2 – 22t + 24 = v(t)
Second, plug in t = 5 to find the velocity at that time:
v(5) = 3(52) – 22(5) + 24 = –11
Third, take the derivative of v(t) to find a(t):
v′(t) = 6t – 22 = a(t)
Finally, plug in t = 5 to find the acceleration at that time:
a(5) = 6(5) – 22 = 8
See the negative velocity? The sign of the velocity is important, because it indicates the direction of the particle. Make sure that you know the following:
When the velocity is negative, the particle is moving to the left.
When the velocity is positive, the particle is moving to the right.
When the velocity and acceleration of the particle have the same signs, the particle’s speed is increasing.
When the velocity and acceleration of the particle have opposite signs, the particle’s speed is decreasing (or slowing down).
When the velocity is zero and the acceleration is not zero, the particle is momentarily stopped and changing direction.
Example 2: If the position of a particle is given by x(t) = t3 – 12t2 + 36t + 18, where t > 0, find the point at which the particle changes direction.
The derivative is:
x′(t) = v(t) = 3t2 – 24t + 36
Set it equal to zero and solve for t:
x′(t) = 3t2 – 24t + 36 = 0
t2 – 8t + 12 = 0
(t – 2)(t – 6) = 0
So, we know that t = 2 or t = 6
You need to check that the acceleration is not 0. x″(t) = 6t – 24. This equals 0 at t = 4. Therefore, the particle is changing direction at t = 2 and t = 6.
Example 3: Given the same position function as in Example 2, find the interval of time during which the particle is slowing down.
When 0 < t < 2 and t > 6, the particle’s velocity is positive; when 2 < t < 6, the particle’s velocity is negative. You can verify this by graphing the function and seeing when it’s above or below the x-axis. Or, try some points in the regions between the roots and outside the roots. Now, we need to determine the same information about the acceleration:
a(t) = v′(t) = 6t – 24
So the acceleration will be negative when t < 4, and positive when t > 4.
So we have:
Whenever the velocity and acceleration have opposite signs, the particle is slowing down. Here the particle is slowing down during the first two seconds (0 < t < 2) and between the fourth and sixth seconds (4 < t < 6).
Another typical question you’ll be asked is to find the distance a particle has traveled from one time to another. This is the distance that the particle has covered without regard to the sign, not just the displacement. In other words, if the particle had an odometer on it, what would it read? Usually, all you have to do is plug the two times into the position function and find the difference.
Example 4: How far does a particle travel between the eighth and tenth seconds if its position function is x(t) = t2 – 6t?
Find x(10) – x(8) = (100 – 60) – (64 – 48) = 24.
Be careful about one very important thing: If the velocity changes sign during the problem’s time interval, you’ll get the wrong answer if you simply follow the method in the paragraph above. For example, suppose we had the same position function as above but we wanted to find the distance that the particle travels from t = 2 to t = 4:
x(4) – x(2) = (–8) – (–8) = 0
This is wrong. The particle travels from –8 back to –8, but it hasn’t stood still. To fix this problem, divide the time interval into the time when the velocity is negative and the time when the velocity is positive, and add the absolute values of each distance. Here, the velocity is v(t) = 2t – 6. The velocity is negative when t < 3 and positive when t > 3. So we find the absolute value of the distance traveled from t = 2 to t = 3 and add to that the absolute value of the distance traveled from t = 3 to t = 4.
Because x(t) = t2 – 6t:
|x(3) − x(2)| + |x(4) − x(3)| = |−9 + 8| + |−8 + 9| = 2
This is the distance that the particle traveled.
Example 5: Given the position function x(t) = t4 – 8t2, find the distance that the particle travels from t = 0 to t = 4.
First, find the first derivative (v(t) = 4t3 – 16t) and set it equal to zero:
4t3 – 16t = 0 4t(t2 – 4) = 0 t = 0, 2, –2
So we need to divide the time interval into t = 0 to t = 2 and t = 2 to t = 4:
|x(2) − x(0)| + |x(4) − x(2)| = 16 + 144 = 160
Here are some solved problems. Do each problem, covering the answer first, then checking your answer.
PROBLEM 1. Find the velocity and acceleration of a particle whose position function is x(t) = 2t3 – 21t2 + 60t + 3, for t > 0.
Answer: Find the first two derivatives:
v(t) = 6t2 – 42t + 60
a(t) = 12t – 42
PROBLEM 2. Given the position function in problem 1, find when the particle’s speed is increasing.
Answer: First, set v(t) = 0:
6t2 – 42t + 60 = 0
t2 – 7t + 10 = 0
(t – 2)(t – 5) = 0
t = 2, t = 5
You should be able to determine that the velocity is positive from 0 < t < 2, negative from 2 < t < 5, and positive again from t > 5.
Now, set a(t) = 0:
12t – 42 = 0
t = 
You should be able to determine that the acceleration is negative from 0 < t < and positive from t > .
The intervals where the velocity and the acceleration have the same sign are 2 < t < and t > 5.
PROBLEM 3. Given that the position of a particle is found by x(t) = t3 – 6t2 + 1; t > 0, find the distance that the particle travels from t = 2 to t = 5.
Answer: First, find v(t).
v(t) = 3t2 – 12t
Second, set v(t) = 0 and find the critical values:
3t2 – 12t = 0 3t(t – 4) = 0 t = {0, 4}
Since the particle changes direction after four seconds, you have to figure out two time intervals separately (from t = 2 to t = 4 and from t = 4 to t = 5) and add the absolute values of the distances:
|x(4) − x(2)| + |x(5) − x(4)| = |(−31) − (−15)| + |(−24) − (−31)| = 23
Now try these problems. The answers are in Chapter 23.
1. Find the velocity and acceleration of a particle whose position function is x(t) = t3 – 9t2 + 24t, t > 0.
2. Find the velocity and acceleration of a particle whose position function is x(t) = sin(2t) + cos(t).
3. If the position function of a particle is 
, t < 0 find when the particle is changing direction.
4. If the position function of a particle is 
, 0 < t < 4π, find when the particle is changing direction.
5. If the position function of a particle is x(t) = 3t2 + 2t + 4, t > 0, find the distance that the particle travels from t = 2 to t = 5.
6. If the position function of a particle is x(t) = t2 + 8t, t > 0, find the distance that the particle travels from t = 0 to t = 4.
7. If the position function of a particle is x(t) = 2sin2t + 2cos2t, t > 0, find the velocity and acceleration of the particle.
8. If the position function of a particle is x(t) = t3 + 8t2 – 2t + 4, t > 0, find when the particle is changing direction.
9. If the position function of a particle is x(t) = 2t3 – 6t2 + 12t – 18, t > 0, find when the particle is changing direction.
10. If the position function of a particle is x(t) = sin2 2t, t > 0, find the distance that the particle travels from t = 0 to t = 2.