and the x-axis (the curve y = 0), from x = 0 to x = 1, and revolve it about the x-axis. The picture looks like this:Does the chapter title leave you in a cold sweat? Don’t worry. You’re not alone. This chapter covers a topic widely seen as one of the most difficult on the AP exam. There is always a volume question on the test. The good news is that you’re almost never asked to evaluate the integral—you usually only have to set it up. The difficulty with this chapter, as with Chapter 16, is that there aren’t any simple rules to follow. You have to draw the picture and figure it out.
In this chapter we’re going to take the region between two curves, rotate it around a line (usually the x- or y-axis), and find the volume of the region. There are two methods of doing this: the washers method and the cylindrical shells method. Sometimes you’ll hear the washers method called the disk method, but a disk is only a washer without a hole in the middle.
Let’s look at the region between the curve y = and the x-axis (the curve y = 0), from x = 0 to x = 1, and revolve it about the x-axis. The picture looks like this:
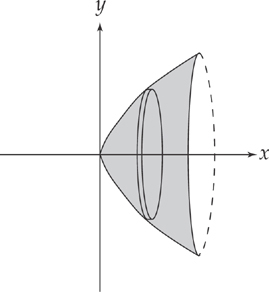
If you slice the resulting solid perpendicular to the x-axis, each cross-section of the solid is a circle, or disk (hence the phrase “disk method”). The radii of the disks vary from one value of x to the next, but you can find each radius by plugging it into the equation for y: Each radius is . The area of each disk is therefore:
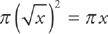
Each disk is infinitesimally thin, so its thickness is dx; if you add up the volumes of all the disks, you’ll get the entire volume. The way to add these up is by using the integral, with the endpoints of the interval as the limits of integration. Therefore, to find the volume, evaluate the integral:
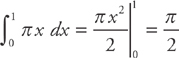
Now, let’s generalize this. If you have a region whose area is bounded by the curve y = f(x) and the x-axis on the interval [a, b], each disk has a radius of f(x), and the area of each disk will be:
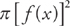
To find the volume, evaluate the integral:
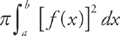
This is the formula for finding the volume using disks.
Example 1: Find the volume of the solid that results when the region between the curve y = x and the x-axis, from x = 0 to x = 1, is revolved about the x-axis.
As always, sketch the region to get a better look at the problem:
When you slice vertically, the top curve is y = x and the limits of integration are from x = 0 to x = 1. Using our formula, we evaluate the integral:
The result is:
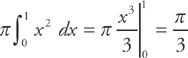
By the way, did you notice that the solid in the problem is a cone with a height and radius of 1? The formula for the volume of a cone is 
πr2h so you should expect to get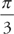 
.
Now, let’s figure out how to find the volume of the solid that results when we revolve a region that does not touch the x-axis. Consider the region bounded above by the curve y = x3 and below by the curve y = x2, from x = 2 to x = 4, which is revolved about the x-axis. Sketch the region first:
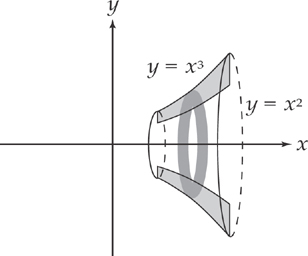
If you slice this region vertically, each cross-section looks like a washer (hence the phrase “washer method”):
The outer radius is R = x3 and the inner radius is r = x2. To find the area of the region between the two circles, take the area of the outer circle, πR2, and subtract the area of the inner circle, πr2.
We can simplify this to:
πR2 − πr2 = π(R2 − r2)
Because the outer radius is R = x3 and the inner radius is r = x2, the area of each region is π(x6 − x4). You can sum up these regions using the integral:
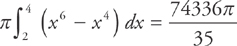
Here’s the general idea: In a region whose area is bounded above by the curve y = f(x) and below by the curve y = g(x), on the interval [a, b], then each washer will have an area of:
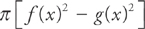
To find the volume, evaluate the integral:
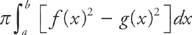
This is the formula for finding the volume using washers when the region is rotated around the x-axis.
Example 2: Find the volume of the solid that results when the region bounded by y = x and y = x2, from x = 0 to x = 1, is revolved about the x-axis.
Sketch it first:
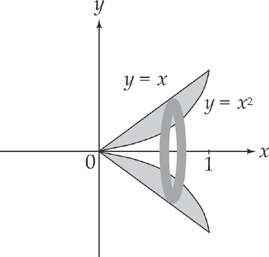
The top curve is y = x and the bottom curve is y = x2 throughout the region. Then our formula tells us that we evaluate the integral:
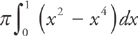
The result is:
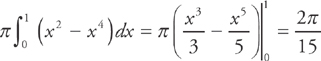
Suppose the region we’re interested in is revolved around the y-axis instead of the x-axis. Now, to find the volume, you have to slice the region horizontally instead of vertically. We discussed how to do this in the previous unit on area.
Now, if you have a region whose area is bounded on the right by the curve x = f(y) and on the left by the curve x = g(y), on the interval [c, d], then each washer has an area of:
To find the volume, evaluate the integral:
This is the formula for finding the volume using washers when the region is rotated about the y-axis.
Example 3: Find the volume of the solid that results when the region bounded by the curve x = y2 and the curve x = y3, from y = 0 to y = 1 is revolved about the y-axis.
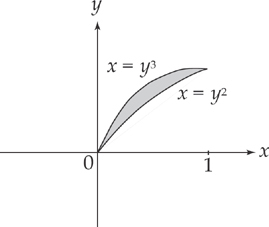
Since x = y2 is always on the outside and x = y3 is always on the inside, you have to evaluate the integral:
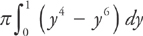
Here’s what you should get:
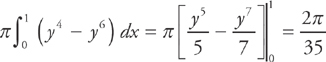
There’s only one more nuance to cover. Sometimes you’ll have to revolve the region about a line instead of one of the axes. If so, this will affect the radii of the washers; you’ll have to adjust the integral to reflect the shift. Once you draw a picture, it usually isn’t too hard to see the difference.
Example 4: Find the volume of the solid that results when the area bounded by the curve y = x2 and the curve y = 4x is revolved about the line y = –2. Set up but do not evaluate the integral. (This is how the AP exam will say it!)
You’re not given the limits of integration here, so you need to find where the two curves intersect by setting the equations equal to each other:
x2 = 4x
x2 – 4x = 0
x = 0, 4
These will be our limits of integration. Next, sketch the curve:
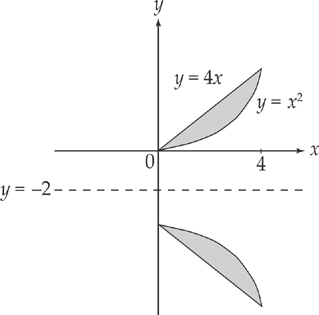
Notice that the distance from the axis of revolution is no longer found by just using each equation. Now, you need to add 2 to each equation to account for the shift in the axis. Thus, the radii are x2 + 2 and 4x + 2. This means that we need to evaluate the integral:
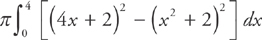
Suppose instead that the region was revolved about the line x = –2. Sketch the region again:
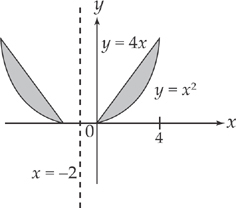
You’ll have to slice the region horizontally this time; this means you’re going to solve each equation for x in terms of y: x =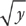 
and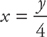 
. We also need to find the y-coordinates of the intersection of the two curves: y = 0, 16.
Notice also that, again, each radius is going to be increased by 2 to reflect the shift in the axis of revolution. Thus we will have to evaluate the integral:
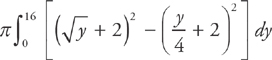
Finding the volumes isn’t that hard, once you’ve drawn a picture, figured out whether you need to slice vertically or horizontally, and determined whether the axis of revolution has been shifted. Sometimes, though, there will be times when you want to slice vertically yet revolve around the y-axis (or slice horizontally yet revolve about the x-axis). Here’s the method for finding volumes in this way.
Let’s examine the region bounded above by the curve y = 2 – x2 and below by the curve y = x2, from x = 0 to x = 1. Suppose you had to revolve the region about the y-axis instead of the x-axis:
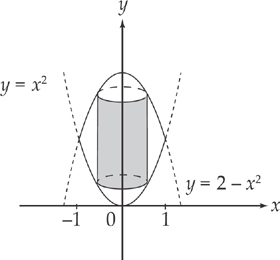
If you slice the region vertically and revolve the slice, you won’t get a washer; you’ll get a cylinder instead. Because each slice is an infinitesimally thin rectangle, the cylinder’s “thickness” is also very, very thin, but real nonetheless. Thus, if you find the surface area of each cylinder and add them up, you’ll get the volume of the region.
We know it’s difficult to visualize, but you must practice drawing these pictures. If you can’t draw the picture, you won’t be able to set up the integral.
The formula for the surface area of a cylinder is 2πrh. The height of the cylinder is the length of the vertical slice, (2 – x2) – x2 = 2 – 2x2 and the radius of the slice is x. Thus, evaluate the integral:
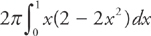
The math goes like this:
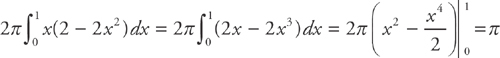
Suppose you tried to slice the region horizontally and use washers. You’d have to convert each equation and find the new limits of integration. Because the region is not bounded by the same pair of curves throughout, you would have to evaluate the region using several integrals. The cylindrical shells method was invented precisely so you can avoid this.
From a general standpoint: If we have a region whose area is bounded above by the curve y = f(x) and below by the curve y = g(x), on the interval [a, b], then each cylinder will have a height of f(x) – g(x), a radius of x, and an area of 2πx[f(x) – g(x)].
To find the volume, evaluate the integral:
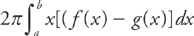
This is the formula for finding the volume using cylindrical shells when the region is rotated around the y-axis.
Example 5: Find the volume of the region that results when the region bounded by the curve y = , the x-axis, and the line x = 9 is revolved about the y-axis. Set up but do not evaluate the integral.
Your sketch should look like this:
Notice that the limits of integration are from x = 0 to x = 9, and that each vertical slice is bounded from above by the curve y = and from below by the x-axis (y = 0). We need to evaluate the integral:
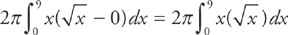
Example 6: Find the volume that results when the region in Example 5 is revolved about the line x = –1. Set up but do not evaluate the integral.
Sketch the figure:
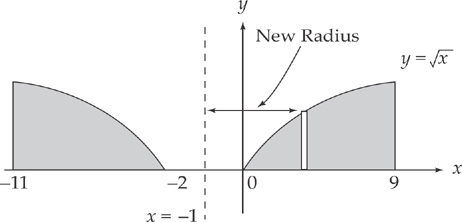
If you slice the region vertically, the height of the shell doesn’t change because of the shift in axis of revolution, but you have to add 1 to each radius.
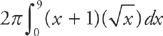
The last formula you need to learn involves slicing the region horizontally and revolving it about the x-axis. As you probably guessed, you’ll get a cylindrical shell.
If you have a region whose area is bounded on the right by the curve x = f(y) and on the left by the curve x = g(y), on the interval [c, d], then each cylinder will have a height of f(y) – g(y), a radius of y, and an area of 2πy[f(y) – g(y)].
To find the volume, evaluate the integral:
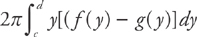
This is the formula for finding the volume using cylindrical shells when the region is rotated around the x-axis.
Example 7: Find the volume of the region that results when the region bounded by the curve x = y3 and the line x = y, from y = 0 to y = 1, is rotated about the x-axis. Set up but do not evaluate the integral.
Let your sketch be your guide:
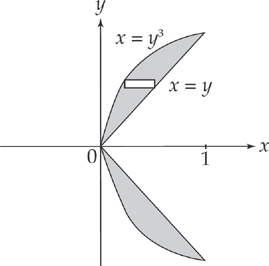
Each horizontal slice is bounded on the right by the curve x = y and on the left by the line x = y3. The integral to evaluate is:
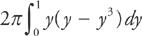
Suppose that you had to revolve this region about the line y = –1 instead. Now the region looks like this:
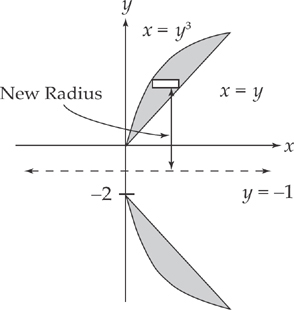
The radius of each cylinder is increased by 1 because of the shift in the axis of revolution, so the integral looks like this:
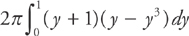
Wasn’t this fun? Volumes of Solids of Revolution require you to sketch the region carefully and to decide whether it’ll be easier to slice the region vertically or horizontally. Once you figure out the slices’ boundaries and the limits of integration (and you’ve adjusted for an axis of revolution, if necessary), it’s just a matter of plugging into the integral. Usually, you won’t be asked to evaluate the integral unless it’s a simple one. Once you’ve conquered this topic, you’re ready for anything.
There is one other type of volume that you need to be able to find. Sometimes, you will be given an object where you know the shape of the base and where perpendicular cross-sections are all the same regular, planar geometric shape. These sound hard, but are actually quite straightforward. This is easiest to explain through an example.
Example 8: Suppose we are asked to find the volume of a solid whose base is the circle x2 + y2 = 4, and where cross-sections perpendicular to the x-axis are all squares whose sides lie on the base of the circle. How would we find the volume?
First, make a drawing of the circle:
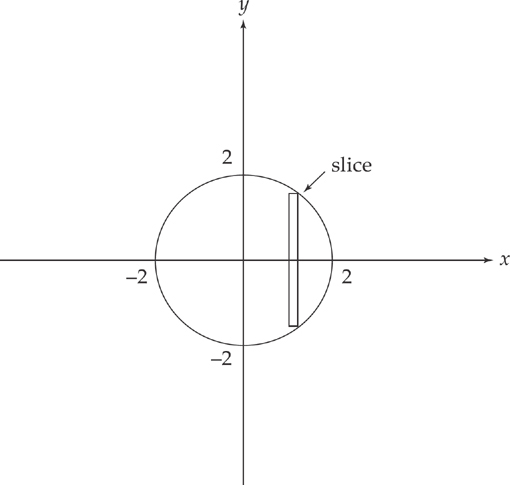
What this problem is telling us is that every time we make a vertical slice, the slice is the length of the base of a square. If we want to find the volume of the solid, all we have to do is integrate the area of the square, from one endpoint of the circle to the other.
The side of the square is the vertical slice whose length is 2y, which we can find by solving the equation of the circle for y and multiplying by 2. We get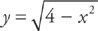 
. Then the length of a side of the square is 
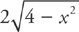. Because the area of a square is side2, we can find the volume by: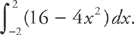 
Let’s perform the integration, although on some problems you will be permitted to find the answer with a calculator.
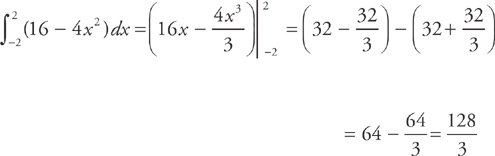
As you can see, the technique is very simple. First you find the side of the cross-section in terms of y. This will involve a vertical slice. Then you plug the side into the equation for the area of the cross-section. Then integrate the area from one endpoint of the base to the other. On the AP exam, cross-sections will be squares, equilateral triangles, circles, or semi-circles, or maybe isosceles right triangles. So here are some handy formulae to know.
Given the side of an equilateral triangle, the area is: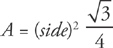 
Given the diameter of a semi-circle, the area is: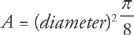 
Given the hypotenuse of an isosceles right triangle, the area is: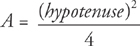 
Example 9: Use the same base as Example 8, except this time the cross-sections are equilateral triangles. We find the side of the triangle just as we did above. It is 2y, which is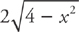 
. Now, because the area of an equilateral triangle is (side)2 
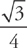, we can find the volume by evaluating the integral 
We get: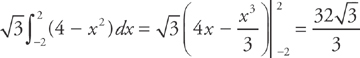 
Example 10: Use the same base as Example 8, except this time the cross-sections are semi-circles whose diameters lie on the base. We find the side of the semi-circle just as we did above. It is 2y, which is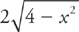 
. Now, because the area of a semi-circle is (diameter)2
, we can find the volume by evaluating the integral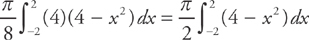 
We get: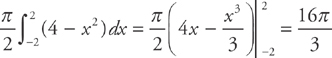 
Here are some solved problems. Do each problem, covering the answer first, then check your answer.
PROBLEM 1. Find the volume of the solid that results when the region bounded by the curve y = 16 – x2 and the curve y = 16 – 4x is rotated about the x-axis. Use the washer method and set up but do not evaluate the integral.
Answer: First, sketch the region:
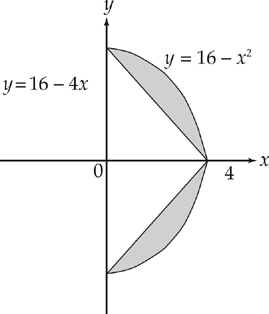
Next, find where the curves intersect by setting the two equations equal to each other:
16 – x2 = 16 – 4x
x2 = 4x
x2 – 4x = 0
x = 0, 4
Slicing vertically, the top curve is always y = 16 – x2 and the bottom is always y = 16 – 4x, so the integral looks like this:
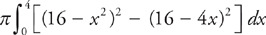
PROBLEM 2. Repeat Problem 1, but revolve the region about the y-axis and use the cylindrical shells method. Set up but do not evaluate the integral.
Answer: Sketch the situation:
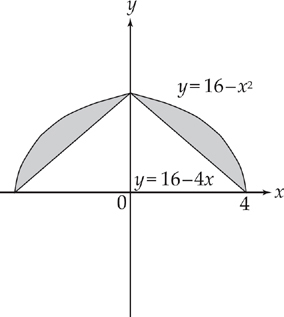
Slicing vertically, the top of each cylinder is y = 16 – x2, the bottom is y = 16 – 4x, and the radius is x. Therefore, you should set up the following:
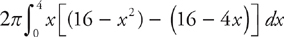
PROBLEM 3. Repeat Problem 1 but revolve the region about the x-axis and use the cylindrical shells method. Set up but do not evaluate the integral.
Answer: Sketch it like this:
To slice horizontally, you have to solve each equation for x in terms of y and find the limits of integration with respect to y. First, solve for x in terms of y:
Next, determine the limits of integration: They’re from y = 0 to y = 16. Slicing horizontally, the curve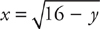 
is always on the right and the curve 
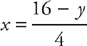is always on the left. The radius is y, so we evaluate:
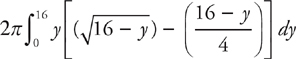
PROBLEM 4. Repeat Problem 1 but revolve the region about the y-axis and use the washers method. Set up but do not evaluate the integral.
Answer: Sketch.
Slicing horizontally, the curve 
is always on the right and the curve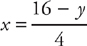 
is always on the left. Therefore, your integral should look like this:
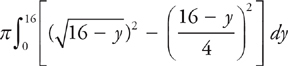
PROBLEM 5. Repeat Problem 1, but revolve the region about the line y = –3. You may use either method. Set up but do not evaluate the integral.
Answer: Your sketch should resemble the one below (note that it’s not drawn exactly to scale):
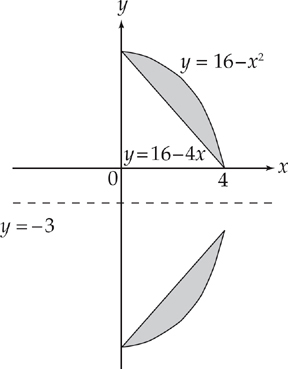
If you were to slice the region vertically, you would use washers. You’ll need to add 3 to each radius to adjust for the axis of revolution. The integral to evaluate is:
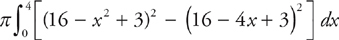
To slice the region horizontally, use cylindrical shells. The radius of each shell would increase by 3, and you would evaluate:
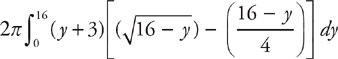
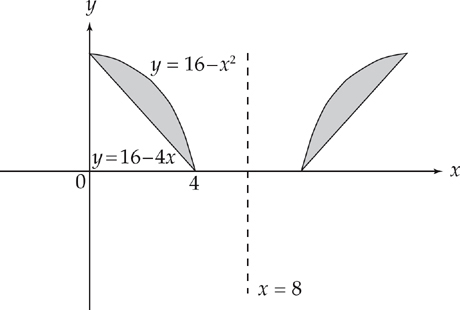
PROBLEM 6. Repeat Problem 1, but revolve the region about the line x = 8. You may use either method. Set up but do not evaluate the integral.
Warning! This one is tricky!
Answer: First, sketch the region.
If you choose cylindrical shells, slice the region vertically; you’ll need to adjust for the axis of revolution. Each radius can be found by subtracting x from 8. (Not 8 from x. That was the tricky part, in case you missed it.) The integral to evaluate is:
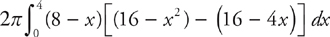
If you choose washers, slice the region horizontally. The radius of each washer is found by subtracting each equation from 8. Notice also that the curve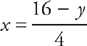 
is now the outer radius of the washer, and the curve 
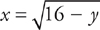is the inner radius. The integral looks like:
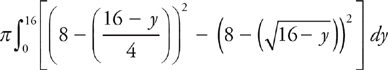
PROBLEM 7: Find the volume of a solid whose base is the region between the x-axis and the curve y = 4 – x2, and whose cross-sections perpendicular to the x-axis are equilateral triangles with a side that lies on the base.
Answer: The curve y = 4 – x2 intersects the x-axis at x = –2 and x = 2. The side of the triangle is 4 – x2, so all that we have to do is evaluate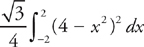 
.
Expand the integrand to get:
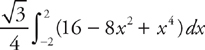
Then integrate, which gives you:
Calculate the volumes below. The answers are in Chapter 23.
1. Find the volume of the solid that results when the region bounded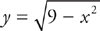 
by and the x-axis is revolved around the x-axis.
2. Find the volume of the solid that results when the region bounded by y = sec x and the x-axis from 
to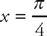 
is revolved around the x-axis.
3. Find the volume of the solid that results when the region bounded by x = 1 – y2 and the y-axis is revolved around the y-axis.
4. Find the volume of the solid that results when the region bounded by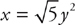 
and the y-axis from y = –1 to y = 1 is revolved around the y-axis.
5. Find the volume of the solid that results when the region bounded by y = x3, x = 2, and the x-axis is revolved around the line x = 2.
6. Use the method of cylindrical shells to find the volume of the solid that results when the region bounded by y = x, x = 2, and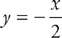 
is revolved around the y-axis.
7. Use the method of cylindrical shells to find the volume of the solid that results when the region bounded by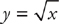 
, y = 2x – 1, and x = 0 is revolved around the y-axis.
8. Use the method of cylindrical shells to find the volume of the solid that results when the region bounded by y = x2, y = 4, and x = 0 is revolved around the x-axis.
9. Use the method of cylindrical shells to find the volume of the solid that results when the region bounded by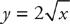 
, x = 4, and y = 0 is revolved around the y-axis.
10. Use the method of cylindrical shells to find the volume of the solid that results when the region bounded by y2 = 8x and x = 2 is revolved around the line x = 4.
11. Find the volume of the solid whose base is the region between the semi-circle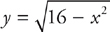 
and the x-axis, and whose cross-sections perpendicular to the x-axis are squares with a side on the base.
12. Find the volume of the solid whose base is the region between y = x2 and y = 4 and whose perpendicular cross-sections are isosceles right triangles with the hypotenuse on the base.