We find the area of a region bounded by f(x) above and g(x) below at all points of the interval [a, b] using the formula 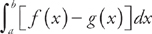 . Here, f(x) = 2 and g(x) = x2 – 2. First, let’s make a sketch of the region:
. Here, f(x) = 2 and g(x) = x2 – 2. First, let’s make a sketch of the region:
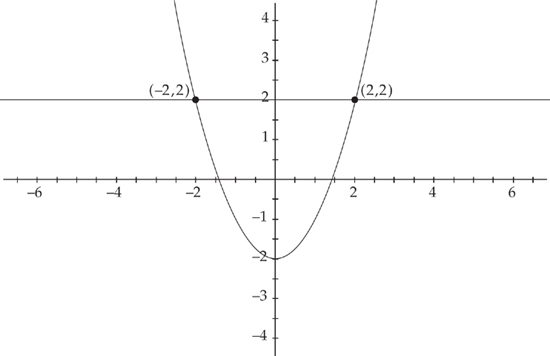
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: x2 – 2 = 2. The solutions are (–2,0) and (2,0). Therefore, in order to find the area of the region, we need to evaluate the integral  . We get:
. We get:
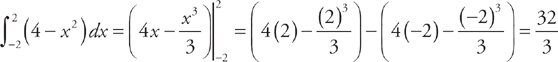 .
.
We find the area of a region bounded by f(x) above and g(x) below at all points of the interval [a,b] using the formula 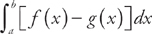 . Here, f(x) = 4x – x2 and g(x) = x2.
. Here, f(x) = 4x – x2 and g(x) = x2.
First, let’s make a sketch of the region:
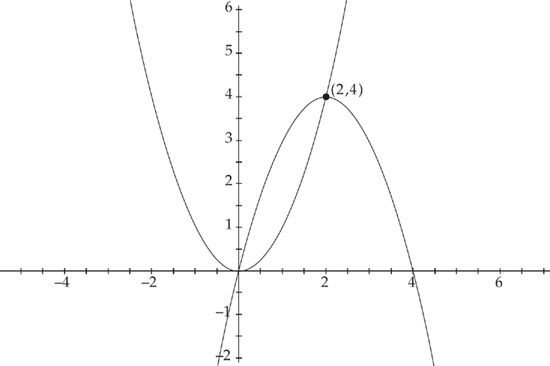
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: 4x – x2 = x2. The solutions are (0,0) and (2,4). Therefore, in order to find the area of the region, we need to evaluate the integral 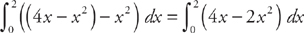 . We get:
. We get: 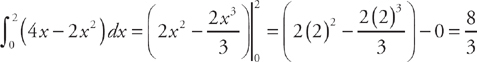 .
.
We find the area of a region bounded by f(x) above and g(x) below at all points of the interval [a, b] using the formula 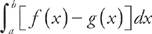 . Here, f(x) = x3 and g(x) = 3x2 – 4.
. Here, f(x) = x3 and g(x) = 3x2 – 4.
First, let’s make a sketch of the region:
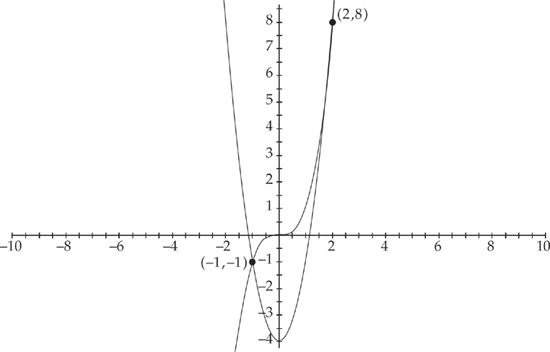
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: 3x2 – 4 = x3. The solutions are (–1, –1) and (2, 8). Therefore, in order to find the area of the region, we need to evaluate the integral 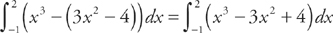 . We get:
. We get: 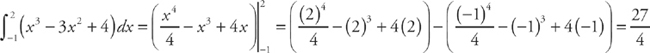
4. 36
We find the area of a region bounded by f(x) above and g(x) below at all points of the interval [a, b] using the formula 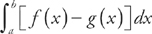 . Here, f(x) = 2x – 5 and g(x) = x2 – 4x – 5.
. Here, f(x) = 2x – 5 and g(x) = x2 – 4x – 5.
First, let’s make a sketch of the region:

Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: x2 – 4x – 5 = 2x – 5. The solutions are (0,–5) and (6,7). Therefore, in order to find the area of the region, we need to evaluate the integral 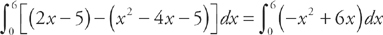 . We get:
. We get:
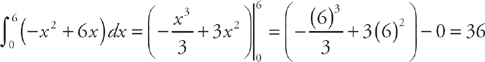 .
.
We find the area of a region bounded by f(x) above and g(x) below at all points of the interval [a, b] using the formula 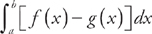 .
.
First, let’s make a sketch of the region:
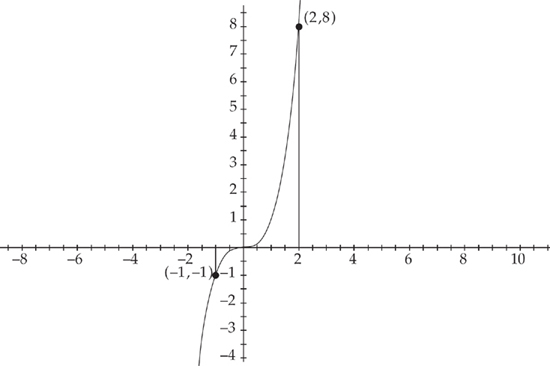
Notice that in the region from x = –1 to x = 0 the top curve is f(x) = 0 (the x‑axis) and the bottom curve is g(x) = x3, but from x = 0 to x = 2 the situation is reversed, so the top curve is f(x) = x3 and the bottom curve is g(x) = 0. Thus, we split the region into two pieces and find the area by evaluating two integrals and adding the answers: 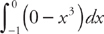 and
and 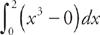 . We get:
. We get: 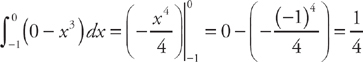 and
and 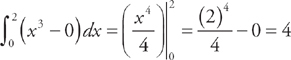 . Therefore, the area of the region is
. Therefore, the area of the region is 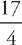 .
.
We find the area of a region bounded by f(y) on the right and g(y) on the left at all points of the interval [c, d] using the formula 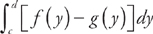 . Here, f(y) = y + 2 and g(y) = y2.
. Here, f(y) = y + 2 and g(y) = y2.
First, let’s make a sketch of the region:
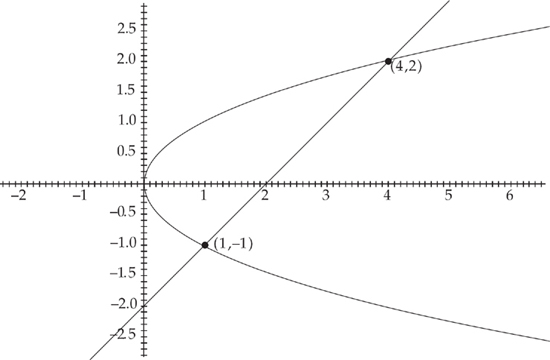
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: y2 = y + 2. The solutions are (4,2) and (1,–1). Therefore, in order to find the area of the region, we need to evaluate the integral 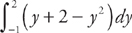 . We get:
. We get:
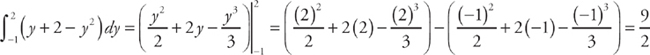
7. 4
We find the area of a region bounded by f(y) on the right and g(y) on the left at all points of the interval [c, d] using the formula 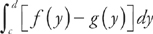 . Here, f(y) = 3 – 2y2 and g(y) = y2.
. Here, f(y) = 3 – 2y2 and g(y) = y2.
First, let’s make a sketch of the region:
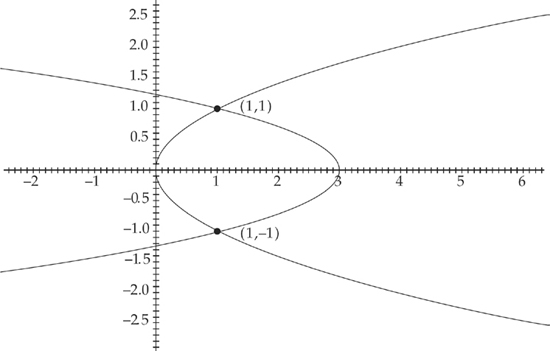
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: y2 = 3 – 2y2. The solutions are (1,1) and (1, –1). Therefore, in order to find the area of the region, we need to evaluate the integral 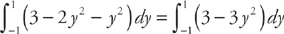 . We get:
. We get:  .
.
We find the area of a region bounded by f(y) on the right and g(y) on the left at all points of the interval [c, d] using the formula 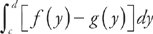 . Here, f(y) = y3 – y2 and g(y) = 2y.
. Here, f(y) = y3 – y2 and g(y) = 2y.
First, let’s make a sketch of the region:
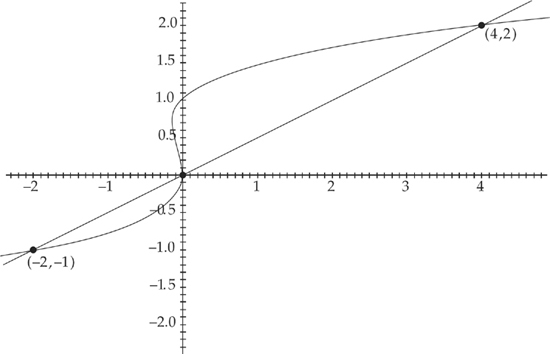
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: y3 – y2 = 2y. The solutions are (4,2), (0,0) and (–2,–1). Notice that in the region from y = –1 to y = 0, the right curve is f(y) = y3 – y2 and the left curve is g(y) = 2y, but from y = 0 to y = 2 the situation is reversed, so the right curve is f(y) = 2y and the left curve is g(y) = y3 – y2. Thus, we split the region into two pieces and find the area by evaluating two integrals and adding the answers: 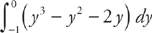 and
and  . We get:
. We get: 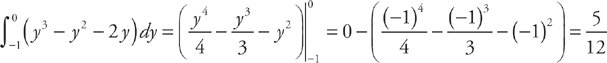 and
and 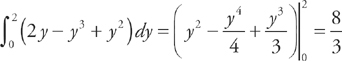 . Therefore, the area of the region is
. Therefore, the area of the region is  .
.
We find the area of a region bounded by f(y) on the right and g(y) on the left at all points of the interval [c, d] using the formula 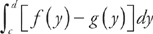 . Here, f(y) = y – 2 and g(y) = y2 – 4y + 2. First, let’s make a sketch of the region:
. Here, f(y) = y – 2 and g(y) = y2 – 4y + 2. First, let’s make a sketch of the region:
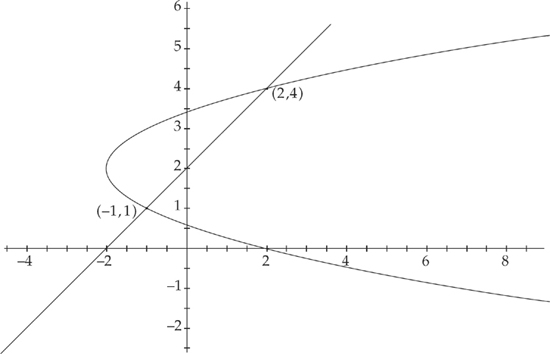
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: y2 – 4y + 2 = y – 2. The solutions are (2,4) and (–1,1). Therefore, in order to find the area of the region, we need to evaluate the integral 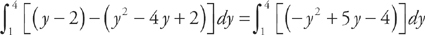 . We get:
. We get: 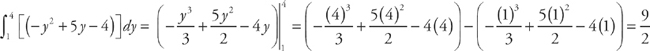
We find the area of a region bounded by f(y) on the right and g(y) on the left at all points of the interval [c, d] using the formula 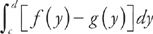 . Here, f(y) = 2 – y4 and
. Here, f(y) = 2 – y4 and 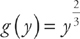 . First, let’s make a sketch of the region:
. First, let’s make a sketch of the region:
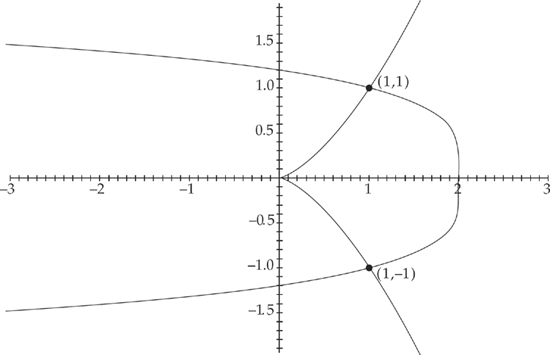
Next, we need to find where the two curves intersect, which will be the endpoints of the region. We do this by setting the two curves equal to each other. We get: 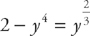 . The solutions are (1,1) and (1,–1). Therefore, in order to find the area of the region, we need to evaluate the integral
. The solutions are (1,1) and (1,–1). Therefore, in order to find the area of the region, we need to evaluate the integral 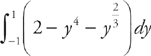 . We get:
. We get: 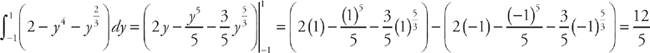
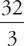

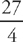


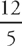
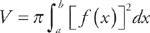 (see
(see 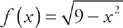 and the x-axis. First, we need to find the endpoints of the region. We do this by setting
and the x-axis. First, we need to find the endpoints of the region. We do this by setting 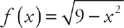 equal to zero and solving for x. We get: x = –3 and x = 3. Thus, we will find the volume by evaluating
equal to zero and solving for x. We get: x = –3 and x = 3. Thus, we will find the volume by evaluating  . We get:
. We get: 
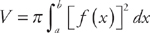 (see
(see 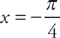 and
and 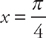 . Thus, we will find the volume by evaluating
. Thus, we will find the volume by evaluating 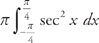 . We get:
. We get: 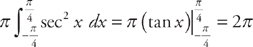 .
.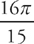
 (see
(see 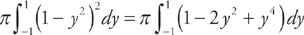 . We get:
. We get:  .
. (see
(see  and the y-axis. We are given the endpoints of the region: y = –1 and y = 1. Thus, we will find the volume by evaluating
and the y-axis. We are given the endpoints of the region: y = –1 and y = 1. Thus, we will find the volume by evaluating 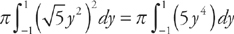 . We get:
. We get: 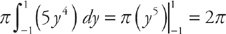 .
.
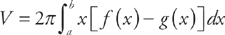 (see
(see 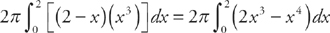 . We get:
. We get: 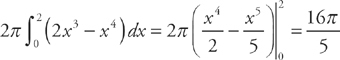 .
.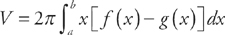 (see
(see  . Thus, the height of each shell is
. Thus, the height of each shell is  and the radius is simply x. The endpoints of our region are x = 0 and x = 2. Therefore, we will find the volume by evaluating:
and the radius is simply x. The endpoints of our region are x = 0 and x = 2. Therefore, we will find the volume by evaluating: 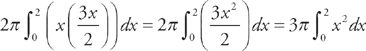 . We get:
. We get:  .
.
 (see
(see  and g(x) = 2x – 1. Thus, the height of each shell is
and g(x) = 2x – 1. Thus, the height of each shell is  and the radius is simply x. The left endpoint of our region is x = 0 and we find the right endpoint by finding where f(x) =
and the radius is simply x. The left endpoint of our region is x = 0 and we find the right endpoint by finding where f(x) =  . We get:
. We get: 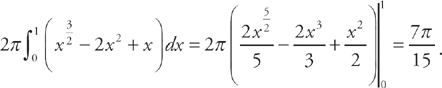 .
.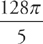
 (see
(see 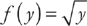 (which we get by solving y = x2 for x) and g(y) = 0 (the y-axis). We can easily see that the top endpoint is y = 4 and the bottom one is y = 0. Therefore, we will find the volume by evaluating:
(which we get by solving y = x2 for x) and g(y) = 0 (the y-axis). We can easily see that the top endpoint is y = 4 and the bottom one is y = 0. Therefore, we will find the volume by evaluating: 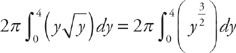 . We get:
. We get: 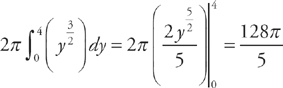 .
.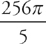
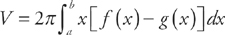 (see
(see  . We get:
. We get: 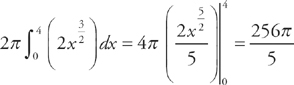 .
.
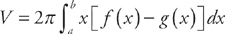 (see
(see 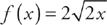 (which we get by solving y2 = 8x for y and taking the top half above the x-axis) and
(which we get by solving y2 = 8x for y and taking the top half above the x-axis) and 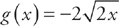 (the bottom half). Thus the height of each shell is
(the bottom half). Thus the height of each shell is  . We can easily see that the left endpoint is x = 0 and that the right endpoint is x = 2. Next, note that we are not revolving around the x-axis but around the line x = 4. Thus, the radius of each shell is not x but rather 4 – x. Therefore, we will find the volume by evaluating:
. We can easily see that the left endpoint is x = 0 and that the right endpoint is x = 2. Next, note that we are not revolving around the x-axis but around the line x = 4. Thus, the radius of each shell is not x but rather 4 – x. Therefore, we will find the volume by evaluating: 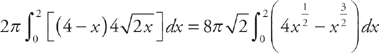 . We get:
. We get: 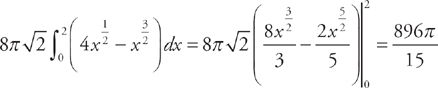 .
.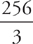
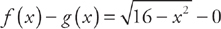 and the intervals are found by setting
and the intervals are found by setting 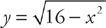 equal to zero. We get: x = –4 and x = 4. Thus, we find the volume by evaluating the integral
equal to zero. We get: x = –4 and x = 4. Thus, we find the volume by evaluating the integral 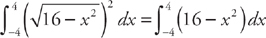 . We get:
. We get:  .
.
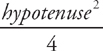 over the endpoints of the interval. Here, the hypotenuses of the triangles are found by f(x) – g(x) = 4 – x2 and the intervals are found by setting y = x2 equal to y = 4. We get: x = –2 and x = 2. Thus, we find the volume by evaluating the integral
over the endpoints of the interval. Here, the hypotenuses of the triangles are found by f(x) – g(x) = 4 – x2 and the intervals are found by setting y = x2 equal to y = 4. We get: x = –2 and x = 2. Thus, we find the volume by evaluating the integral 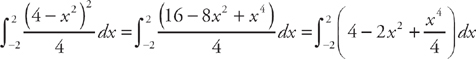 . We get:
. We get:  .
.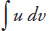 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is: 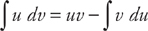 (see
(see 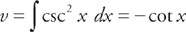 . Plugging into the formula, we get:
. Plugging into the formula, we get: 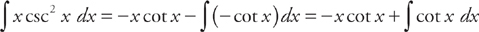 . Now we just have to find
. Now we just have to find 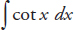 . We do this by rewriting the integrand in terms of sin x and cos x:
. We do this by rewriting the integrand in terms of sin x and cos x: 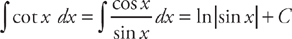 . Therefore,
. Therefore, 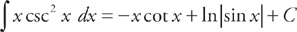 .
.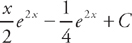
 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is:  (see
(see 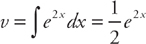 . Plugging into the formula, we get:
. Plugging into the formula, we get:  . Now we just have to find
. Now we just have to find 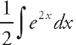 :
: 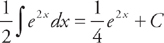 . Therefore,
. Therefore, 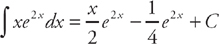 .
.
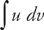 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is:  (see
(see  , then we can find du by taking the derivative of u, and we can find v by taking the integral of dv. We get:
, then we can find du by taking the derivative of u, and we can find v by taking the integral of dv. We get: 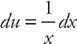 and
and  . Plugging into the formula, we get:
. Plugging into the formula, we get:  . Now we just have to find
. Now we just have to find  . Therefore,
. Therefore, 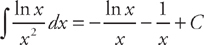 .
. , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is:  (see
(see 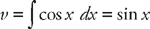 . Plugging into the formula, we get:
. Plugging into the formula, we get: 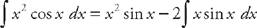 . Now we have to find
. Now we have to find 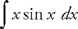 . Once again we will have to use integration by parts. This time, if we let u = x and dv = sin x dx, then du = dx and
. Once again we will have to use integration by parts. This time, if we let u = x and dv = sin x dx, then du = dx and 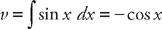 . Plugging into the formula, we get:
. Plugging into the formula, we get: 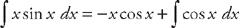 . Finally, we have to find
. Finally, we have to find  . Putting everything together, we get:
. Putting everything together, we get:  .
.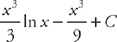
 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is: 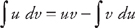 (see
(see  and
and 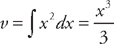 . Plugging into the formula, we get:
. Plugging into the formula, we get:  . Now we just have to find
. Now we just have to find 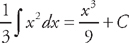 . Therefore,
. Therefore,  .
.
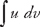 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is:  (see
(see 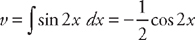 . Plugging into the formula, we get:
. Plugging into the formula, we get: 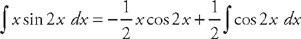 . Now we just have to find
. Now we just have to find 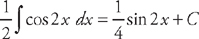 . Therefore,
. Therefore, 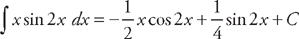 .
.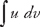 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is: 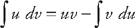 (see
(see 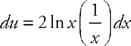 and
and 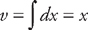 . Plugging into the formula, we get:
. Plugging into the formula, we get:  . Now we have to find
. Now we have to find 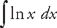 . Once again we will have to use integration by parts. This time, if we let u = ln x and dv = dx, then
. Once again we will have to use integration by parts. This time, if we let u = ln x and dv = dx, then 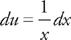 and
and  . Plugging into the formula, we get:
. Plugging into the formula, we get: 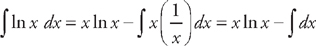 . Finally we have to find
. Finally we have to find 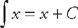 . Putting everything together, we get:
. Putting everything together, we get:  .
.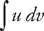 , where both u and v are functions of x. The formula for evaluating the integral is:
, where both u and v are functions of x. The formula for evaluating the integral is: 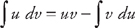 (see
(see  . Plugging into the formula, we get:
. Plugging into the formula, we get: 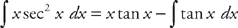 . Now we just have to find
. Now we just have to find 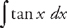 . We do this by rewriting the integrand in terms of sin x and cos x:
. We do this by rewriting the integrand in terms of sin x and cos x: 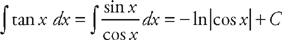 . Therefore,
. Therefore, 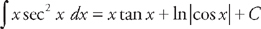 .
.
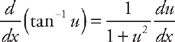 (see
(see  , so
, so 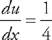 . Therefore,
. Therefore, 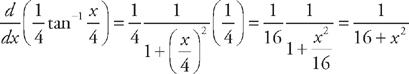 .
.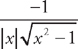
 (see
(see  , so
, so 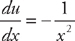 . Therefore,
. Therefore,  .
.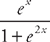
 (see
(see 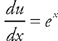 . Therefore,
. Therefore, 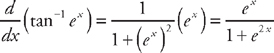 .
.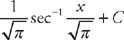
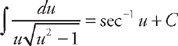 (see
(see 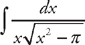 and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor
and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor 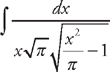 . Next, we do u-substitution. Let
. Next, we do u-substitution. Let 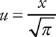 and
and 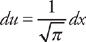 . Multiply both by
. Multiply both by 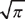 so that
so that 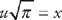 and
and 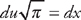 . Substituting into the integrand we get:
. Substituting into the integrand we get: 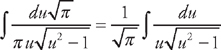 . Now we get:
. Now we get: 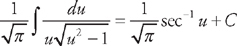 . Substituting back we get:
. Substituting back we get:  .
.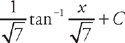
 (see
(see 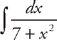 and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor 7 out of the denominator we get:
and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor 7 out of the denominator we get:  . Next, we do u-substitution. Let
. Next, we do u-substitution. Let  and
and 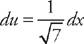 . Multiply du by
. Multiply du by 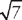 so that
so that 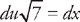 . Substituting into the integrand we get:
. Substituting into the integrand we get:  . Now we get:
. Now we get: 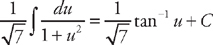 . Substituting back we get:
. Substituting back we get: 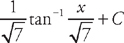 .
.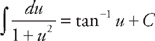 (see
(see 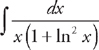 and we will need to do u-substitution. Let u = ln x and
and we will need to do u-substitution. Let u = ln x and 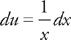 . Substituting into the integrand we get:
. Substituting into the integrand we get: 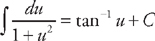 . Substituting back we get: tan–1(ln x) + C.
. Substituting back we get: tan–1(ln x) + C.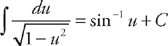 (see
(see 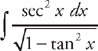 and we will need to do u-substitution. Let u = tan x and du = sec2 x dx. Substituting into the integrand we get:
and we will need to do u-substitution. Let u = tan x and du = sec2 x dx. Substituting into the integrand we get:  . Substituting back we get: sin–1(tan x) + C.
. Substituting back we get: sin–1(tan x) + C.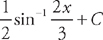
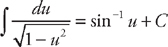 (see
(see 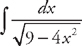 and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor 9 out of the radicand we get:
and we just need to rearrange the integrand so that it is in the proper form to use the integral formula. If we factor 9 out of the radicand we get: 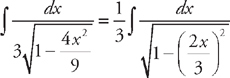 . Next, we do u-substitution. Let
. Next, we do u-substitution. Let 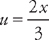 and
and  . Multiply du by
. Multiply du by  so that
so that  . Substituting back we get:
. Substituting back we get: 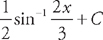 .
.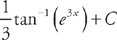
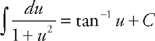 (see
(see 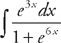 and we will need to do u-substitution. Let u = e3x and du = 3e3x dx. Divide du by 3 so that
and we will need to do u-substitution. Let u = e3x and du = 3e3x dx. Divide du by 3 so that 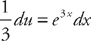 . Substituting into the integrand we get:
. Substituting into the integrand we get: 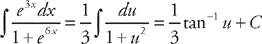 . Substituting back we get:
. Substituting back we get: 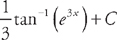 .
.
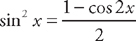 into the integrand. We get:
into the integrand. We get: 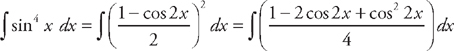 . We can break this into three integrals:
. We can break this into three integrals: 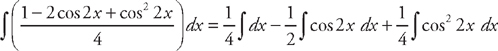 . The first two integrals are easy:
. The first two integrals are easy: 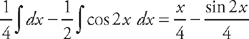 . For the third integral, we use the substitution
. For the third integral, we use the substitution 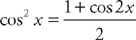 . We get:
. We get:  . Now we integrate these:
. Now we integrate these: 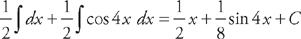 . Now we put everything together to get:
. Now we put everything together to get: 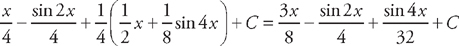 .
.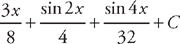
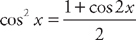 into the integrand. We get:
into the integrand. We get: 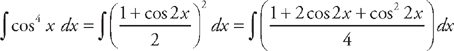 . We can break this into three integrals:
. We can break this into three integrals:  . The first two integrals are easy:
. The first two integrals are easy: 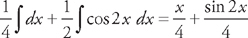 . For the third integral, we again use the substitution
. For the third integral, we again use the substitution 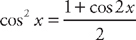 . We get:
. We get: 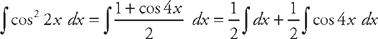 . Now we integrate these:
. Now we integrate these: 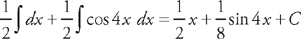 . Now we put everything together to get:
. Now we put everything together to get: 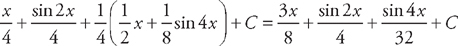 .
.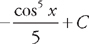
 . Now we substitute back:
. Now we substitute back: 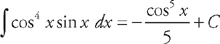 .
.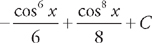
 . Next, we use the trig identity sin2 x = 1 – cos2 x and substitute into the integrand:
. Next, we use the trig identity sin2 x = 1 – cos2 x and substitute into the integrand: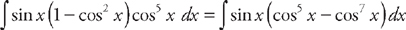 . Now we can use u‑substitution.
. Now we can use u‑substitution. 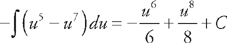 . Now we substitute back:
. Now we substitute back: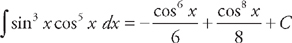 .
.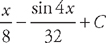
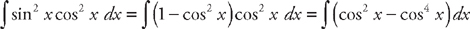 . Next, we use the substitution
. Next, we use the substitution  into the integrand:
into the integrand:  . We use a little algebra:
. We use a little algebra:
 . The first integral is easy:
. The first integral is easy: 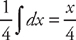 . For the second integral, we again use the substitution
. For the second integral, we again use the substitution  into the integrand:
into the integrand: 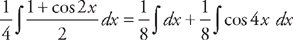 . These are both easy to integrate:
. These are both easy to integrate: 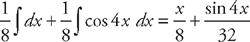 . Putting it all together, we get:
. Putting it all together, we get:  .
.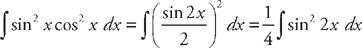 . Now, we can use the substitution
. Now, we can use the substitution 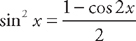 to rewrite the integrand:
to rewrite the integrand: . This is easy to integrate:
. This is easy to integrate:  . This is why you should know your trigonometric identities really well before you take calculus!
. This is why you should know your trigonometric identities really well before you take calculus!
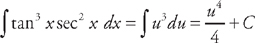 . Now we substitute back:
. Now we substitute back: 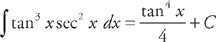 .
.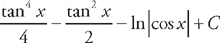
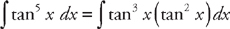 . Next, we use the trigonometric identity tan2 x = sec2 x – 1 and rewrite the integrand:
. Next, we use the trigonometric identity tan2 x = sec2 x – 1 and rewrite the integrand: 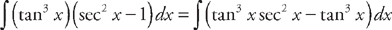 . Now we break this into two integrals:
. Now we break this into two integrals: 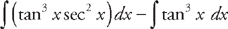 . Next, break up the integrand of the second integral into
. Next, break up the integrand of the second integral into 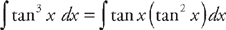 . Once again, use the trigonometric identity tan2 x = sec2 x – 1 to rewrite the integrand:
. Once again, use the trigonometric identity tan2 x = sec2 x – 1 to rewrite the integrand: 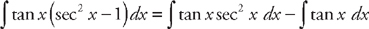 . Putting the integrals
. Putting the integrals 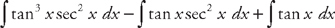 . We can use u-substitution to find the first two integrals. If we let u = tan x, then du = sec2 x dx. Substituting into the integrand, we get:
. We can use u-substitution to find the first two integrals. If we let u = tan x, then du = sec2 x dx. Substituting into the integrand, we get: 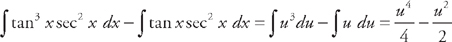 . Substituting back, we get:
. Substituting back, we get: 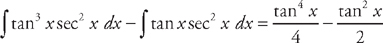 . The last integral we have done before (see
. The last integral we have done before (see 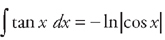 . Therefore
. Therefore 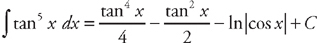 .
.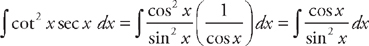 . Next, we do u‑substitution. If we let u = sin x, then du = cos x dx. Substituting into the integrand, we get:
. Next, we do u‑substitution. If we let u = sin x, then du = cos x dx. Substituting into the integrand, we get:  . Substituting back, we get:
. Substituting back, we get: 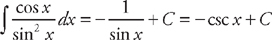 .
.
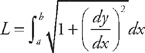 (see
(see 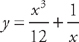 from x = 1 to x = 2. First, we need to find the derivative:
from x = 1 to x = 2. First, we need to find the derivative: 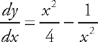 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 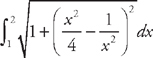 . Now we need to use
. Now we need to use 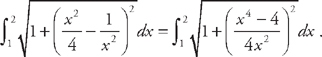 .
. .
.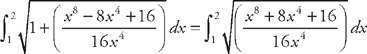 .
.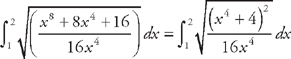 .
.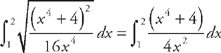 .
. .
.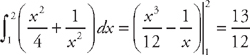 .
.
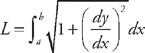 (see
(see 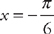 to x = 0. First, we need to find the derivative:
to x = 0. First, we need to find the derivative: 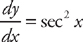 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 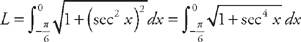 .
.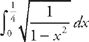
 (see
(see 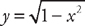 from x = 0 to x =
from x = 0 to x =  . First, we need to find the derivative:
. First, we need to find the derivative: 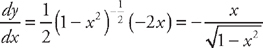 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length:  .
.
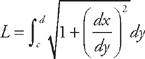 (see
(see 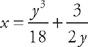 from y = 2 to y = 3. First, we need to find the derivative:
from y = 2 to y = 3. First, we need to find the derivative: 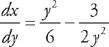 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 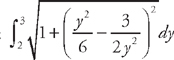 . Now we need to use some algebra to simplify the integrand:
. Now we need to use some algebra to simplify the integrand: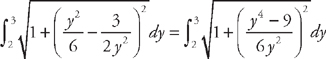 .
.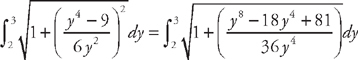 .
.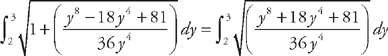 .
.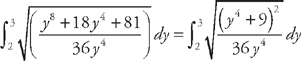 .
. .
.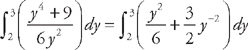 .
.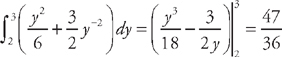 .
.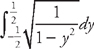
 (see
(see 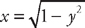 from y = −
from y = −  to y =
to y = 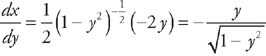 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 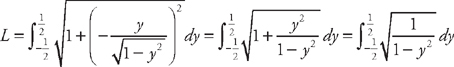 .
.
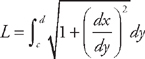 (see
(see  . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 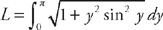 .
.
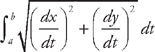 . Here, we have x = cos t and y = sin t from t =
. Here, we have x = cos t and y = sin t from t = 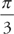 . First, we need to find the derivatives:
. First, we need to find the derivatives: 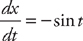 and
and 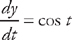 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length:  . Next, we use the trigonometric identity sin2 t + cos2 t = 1 to rewrite the integrand:
. Next, we use the trigonometric identity sin2 t + cos2 t = 1 to rewrite the integrand: 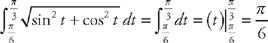 .
.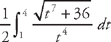
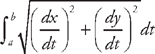 . Here, we have x =
. Here, we have x =  and
and 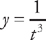 from t = 1 to t = 4. First, we need to find the derivatives:
from t = 1 to t = 4. First, we need to find the derivatives: 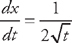 and
and 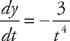 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length:  . With a little algebra, we get:
. With a little algebra, we get: 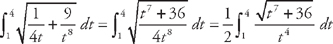 .
.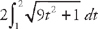
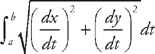 . Here, we have x = 3t2 and y = 2t from t = 1 to t = 2. First, we need to find the derivatives:
. Here, we have x = 3t2 and y = 2t from t = 1 to t = 2. First, we need to find the derivatives: 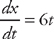 and
and 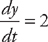 . Now we plug this into the formula for the length:
. Now we plug this into the formula for the length: 
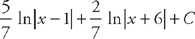
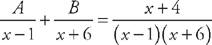 . First, we multiply through by (x – 1)(x + 6): A(x + 6) + B(x – 1) = x + 4.
. First, we multiply through by (x – 1)(x + 6): A(x + 6) + B(x – 1) = x + 4.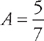 and
and 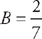 . This means that we can rewrite the integral as:
. This means that we can rewrite the integral as:  . We can easily integrate these:
. We can easily integrate these: 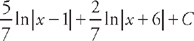 .
.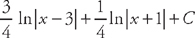
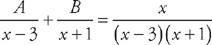 . First, we multiply through by (x – 3)(x + 1): A(x + 1) + B(x – 3) = x
. First, we multiply through by (x – 3)(x + 1): A(x + 1) + B(x – 3) = x and
and 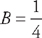 . This means that we can rewrite the integral as:
. This means that we can rewrite the integral as: 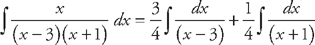 . We can easily integrate these:
. We can easily integrate these: 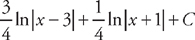 .
.
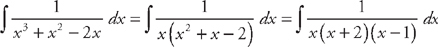 .
.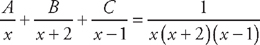 .
. , and
, and 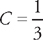 . This means that we can rewrite the integral as:
. This means that we can rewrite the integral as: 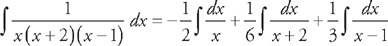 . We can easily integrate these:
. We can easily integrate these: 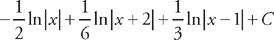 .
.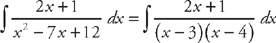 .
.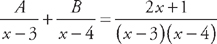 .
.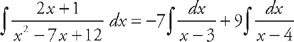 . We can easily integrate these: −7 ln |x − 3| + 9 ln |x − 4| + C.
. We can easily integrate these: −7 ln |x − 3| + 9 ln |x − 4| + C.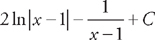
 .
.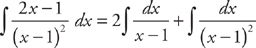 .
.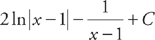 .
.
 .
.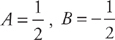 , and
, and  .
. .
.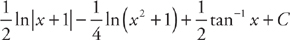 . If you had trouble with these integrals, you should review the sections on logarithmic and trigonometric integrals.
. If you had trouble with these integrals, you should review the sections on logarithmic and trigonometric integrals.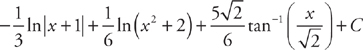
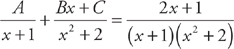 .
.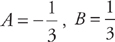 , and
, and 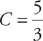 .
.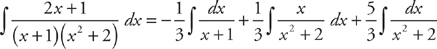 .
.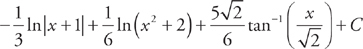 . If you had trouble with these integrals, you should review the sections on logarithmic and trigonometric integrals.
. If you had trouble with these integrals, you should review the sections on logarithmic and trigonometric integrals.
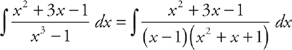 .
.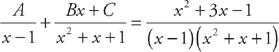 .
.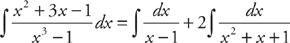 . The first integral is easy:
. The first integral is easy: 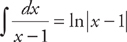 . The second takes a little work and will be a good test of your algebra. First, complete the square to rewrite the denominator:
. The second takes a little work and will be a good test of your algebra. First, complete the square to rewrite the denominator: 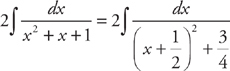 .
.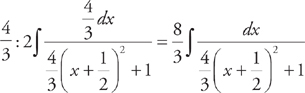 . This can be rewritten as:
. This can be rewritten as:  . Now we do u-substitution. If we let
. Now we do u-substitution. If we let 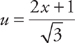 , then
, then 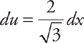 . Multiply du by
. Multiply du by 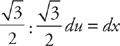 . Now we can substitute into the integrand:
. Now we can substitute into the integrand: 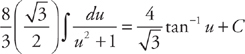 . Substituting back, we get:
. Substituting back, we get: 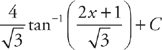 . Now we can put both integrals together:
. Now we can put both integrals together:  .
.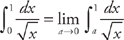 . Now we evaluate the integral:
. Now we evaluate the integral:  . Finally, we take the limit:
. Finally, we take the limit: 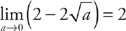 .
.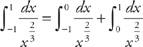 and second, replacing the limit with a and taking the limit of the integral as a approaches 0,
and second, replacing the limit with a and taking the limit of the integral as a approaches 0, 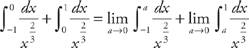 . Now we evaluate the integrals:
. Now we evaluate the integrals: 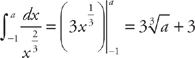 and
and 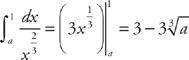 .
.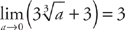 and
and 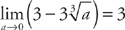 . Therefore, the integral is 3 + 3 = 6.
. Therefore, the integral is 3 + 3 = 6.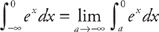 . Now we evaluate the integral:
. Now we evaluate the integral:  . Finally, we take the limit:
. Finally, we take the limit: 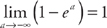 .
.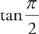 is also undefined. We remedy this by replacing the upper limit with b and taking the limit of the integral as b approaches
is also undefined. We remedy this by replacing the upper limit with b and taking the limit of the integral as b approaches  . And we overcome the two limits difficulty by splitting the integral into two parts at a value where we know that we can integrate and take each limit separately. A simple place to split the integral is at x = 0. We get:
. And we overcome the two limits difficulty by splitting the integral into two parts at a value where we know that we can integrate and take each limit separately. A simple place to split the integral is at x = 0. We get:  . Now we evaluate the integrals:
. Now we evaluate the integrals:  and
and 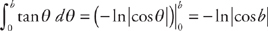 .
. and
and  . Neither limit exists, so the integral diverges. As a general rule, a trigonometric integral (but not an inverse trig one) is going to diverge if one of the limits of integration is infinite.
. Neither limit exists, so the integral diverges. As a general rule, a trigonometric integral (but not an inverse trig one) is going to diverge if one of the limits of integration is infinite.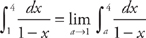 . Now we evaluate the integral:
. Now we evaluate the integral:  . Finally, we take the limit:
. Finally, we take the limit: 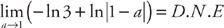 . Therefore, the integral diverges.
. Therefore, the integral diverges.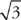
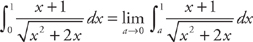 . Now we evaluate the integral. If we let u = x2 + 2x, then du = (2x + 2)dx. If we divide du by 2, we get
. Now we evaluate the integral. If we let u = x2 + 2x, then du = (2x + 2)dx. If we divide du by 2, we get 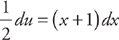 . Now we can substitute into the integrand. Let’s ignore the limits of integration until we substitute back. We get:
. Now we can substitute into the integrand. Let’s ignore the limits of integration until we substitute back. We get: 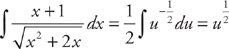 . Now we substitute back and evaluate at the limits of integration:
. Now we substitute back and evaluate at the limits of integration: 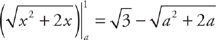 . Finally, we take the limit:
. Finally, we take the limit: 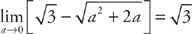 .
.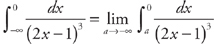 . Now we evaluate the integral:
. Now we evaluate the integral: 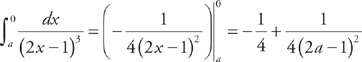 . Finally, we take the limit:
. Finally, we take the limit: 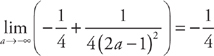 .
.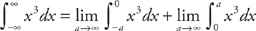 . Now we evaluate the integrals:
. Now we evaluate the integrals: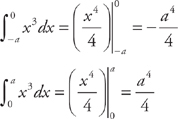
 and
and 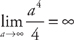 . Therefore, the integral diverges. This is a tricky integral. Notice that if the limits of integration were finite and equal to each other, we would always get zero. It is easy to see this if we graph the function y = x3 and look at the areas on each side of the y-axis. They will always cancel each other because of symmetry.
. Therefore, the integral diverges. This is a tricky integral. Notice that if the limits of integration were finite and equal to each other, we would always get zero. It is easy to see this if we graph the function y = x3 and look at the areas on each side of the y-axis. They will always cancel each other because of symmetry.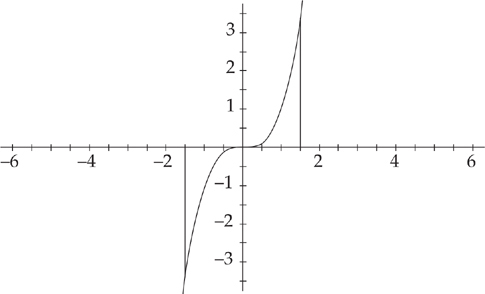
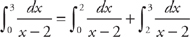 and, second, replacing the limit with a and taking the limit of the integral as a approaches 2,
and, second, replacing the limit with a and taking the limit of the integral as a approaches 2, 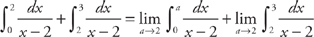 . Now we evaluate the integrals:
. Now we evaluate the integrals: 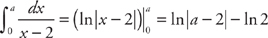 and
and 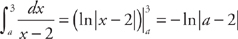 .
.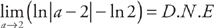 and
and 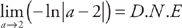 .
.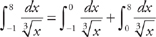 and second, replacing the limit with a and taking the limit of the integral as a approaches 0,
and second, replacing the limit with a and taking the limit of the integral as a approaches 0, 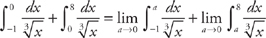 . Now we evaluate the integrals:
. Now we evaluate the integrals: 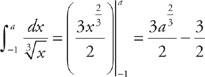 and
and 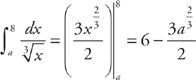 .
.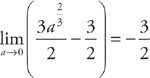 and
and  . Therefore, the integral is
. Therefore, the integral is 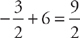 .
.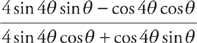
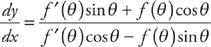 (see
(see 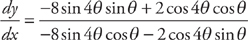 , which can be reduced to
, which can be reduced to 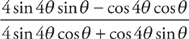 .
.
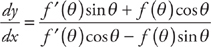 (see
(see 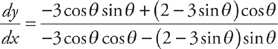 . Now we evaluate the slope at (r, θ) = (2, π):
. Now we evaluate the slope at (r, θ) = (2, π): 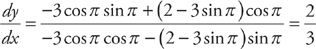 .
.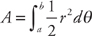 (see
(see 
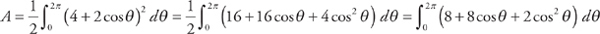 . We can break this into three integrals:
. We can break this into three integrals:  . We can easily evaluate the first two integrals:
. We can easily evaluate the first two integrals:  and
and 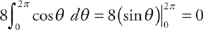 . The third integral requires us to use the trigonometric substitution
. The third integral requires us to use the trigonometric substitution 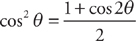 (see
(see 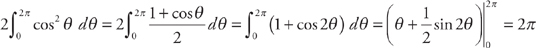 . Therefore, the area is 18π.
. Therefore, the area is 18π. (see
(see 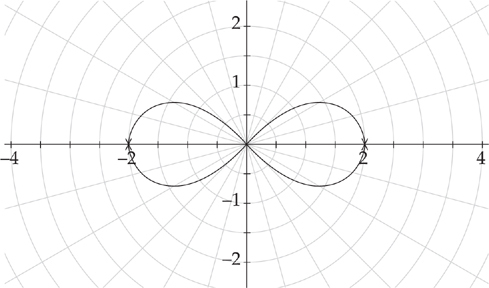
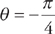 to
to 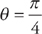 . Plugging into the formula, we get:
. Plugging into the formula, we get:
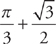
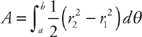 (see
(see 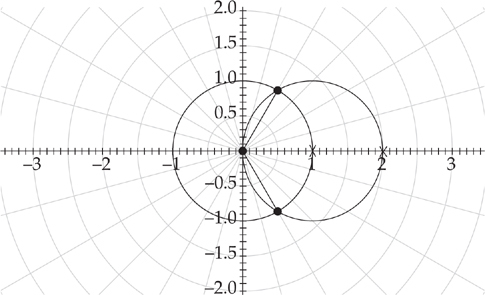
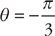 to
to 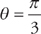 . Plugging into the formula, we get:
. Plugging into the formula, we get: 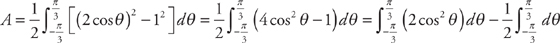 . The first integral requires us to use the trigonometric substitution
. The first integral requires us to use the trigonometric substitution 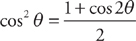 (see
(see  . The second integral is simply
. The second integral is simply 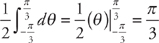 . Therefore, the area is
. Therefore, the area is 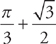 .
.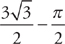
 (see
(see 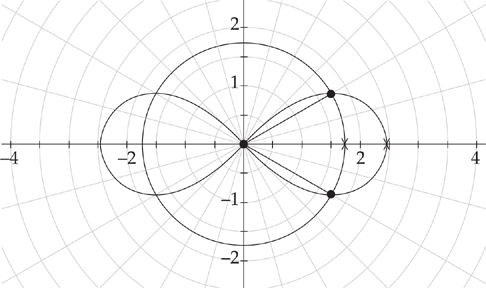
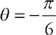 to
to 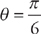 . Plugging into the formula, we get:
. Plugging into the formula, we get: 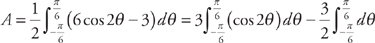 . Evaluating the integrals, we get:
. Evaluating the integrals, we get: 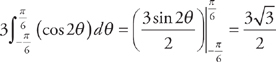 and
and 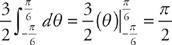 . Therefore, the area is
. Therefore, the area is 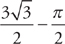 .
.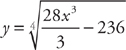
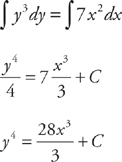
 .
.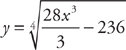 .
.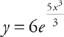
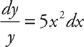 . Next, we integrate both sides:
. Next, we integrate both sides: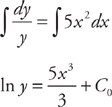
 . We can rewrite this as
. We can rewrite this as 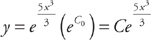 .
.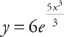 .
.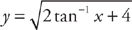
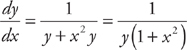 . Next, we multiply both sides by y and by dx. We get:
. Next, we multiply both sides by y and by dx. We get: 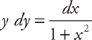 . Next, we integrate both sides:
. Next, we integrate both sides:


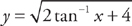 .
.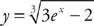
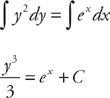
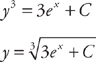

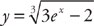 .
.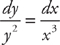 . Next, we integrate both sides:
. Next, we integrate both sides: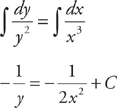
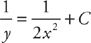
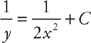 , which can be rewritten as y = 2x2.
, which can be rewritten as y = 2x2.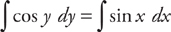
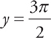 :
: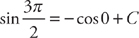
 , where k is a constant and y is the population at a time t. Here we are also told that y = 4,000 at t = 0 and y = 6,500 at t = 3. We solve this differential equation by separation of variables. We want to get all of the y variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by y and multiplying both sides by dt. We get:
, where k is a constant and y is the population at a time t. Here we are also told that y = 4,000 at t = 0 and y = 6,500 at t = 3. We solve this differential equation by separation of variables. We want to get all of the y variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by y and multiplying both sides by dt. We get: 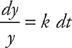 . Next, we integrate both sides:
. Next, we integrate both sides: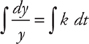
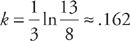 .
.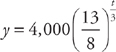 . Finally, we can solve for the population at time t = 10: y ≈ 4,000e.162(10) or
. Finally, we can solve for the population at time t = 10: y ≈ 4,000e.162(10) or 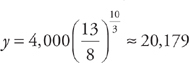 . (Notice how even with an “exact” solution, we still have to round the answer. And, if we are concerned with significant figures, the population can be written as 20,000.)
. (Notice how even with an “exact” solution, we still have to round the answer. And, if we are concerned with significant figures, the population can be written as 20,000.) . We are also told that v = 18 and h = 45 when t = 0. We solve this differential equation by separation of variables. We want to get all of the v variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by multiplying both sides by dt: dv = –9 dt. Next, we integrate both sides:
. We are also told that v = 18 and h = 45 when t = 0. We solve this differential equation by separation of variables. We want to get all of the v variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by multiplying both sides by dt: dv = –9 dt. Next, we integrate both sides:
 . We again separate the variables by multiplying both sides by dt: dh = (–9t + 18) dt. We integrate both sides:
. We again separate the variables by multiplying both sides by dt: dh = (–9t + 18) dt. We integrate both sides: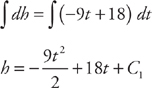
 , so C1 = 45
, so C1 = 45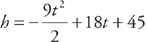 .
.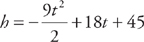
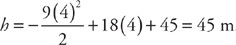
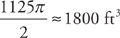
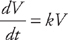 where k is a constant and V is the volume of the sphere at time t. We are also told that V = 36π when t = 0 and V = 90π when t = 1. We solve this differential equation by separation of variables. We want to get all of the V variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by V and multiplying both sides by dt. We get:
where k is a constant and V is the volume of the sphere at time t. We are also told that V = 36π when t = 0 and V = 90π when t = 1. We solve this differential equation by separation of variables. We want to get all of the V variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by V and multiplying both sides by dt. We get: 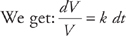 . Next, we integrate both sides:
. Next, we integrate both sides: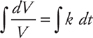
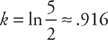
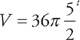 . Finally, we can solve for the volume at time t = 3: V ≈ 36πe.916(3) ≈ 1766ft3 or
. Finally, we can solve for the volume at time t = 3: V ≈ 36πe.916(3) ≈ 1766ft3 or 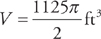 . (And, if we are concerned with significant figures, the volume can be written as 1800.)
. (And, if we are concerned with significant figures, the volume can be written as 1800.)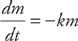 , where m is the mass at time t. We are also given that m = 10,000 when t = 0 and m = 5,000 when t = 5,750. We solve this differential equation by separation of variables. We want to get all of the m variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by m and multiplying both sides by dt. We get:
, where m is the mass at time t. We are also given that m = 10,000 when t = 0 and m = 5,000 when t = 5,750. We solve this differential equation by separation of variables. We want to get all of the m variables on one side of the equals sign and all of the t variables on the other side. We can do this easily by dividing both sides by m and multiplying both sides by dt. We get: 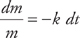 . Next, we integrate both sides:
. Next, we integrate both sides: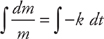
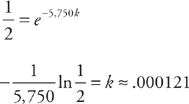
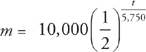 .
.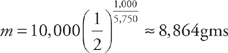 . (And, if we are concerned with significant figures, the mass can be written as 8,900.)
. (And, if we are concerned with significant figures, the mass can be written as 8,900.)

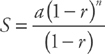 , where a is the first term of the series and r is the common ratio (see
, where a is the first term of the series and r is the common ratio (see  . Plugging into the formula, we get:
. Plugging into the formula, we get: 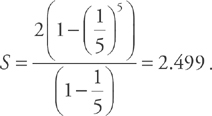 .
.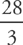
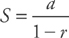 , where a is the first term of the series and r is the common ratio (see
, where a is the first term of the series and r is the common ratio (see  . Plugging into the formula, we get:
. Plugging into the formula, we get: 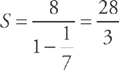 .
. and
and 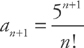 . Plugging into the test, we get:
. Plugging into the test, we get:  . Therefore, the series converges.
. Therefore, the series converges.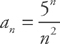 and
and  . Plugging into the test, we get:
. Plugging into the test, we get: 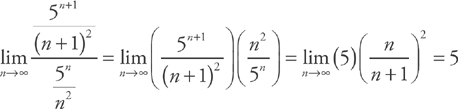 . Therefore, the series diverges.
. Therefore, the series diverges.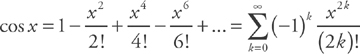
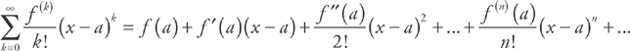

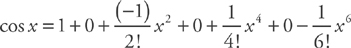 .
.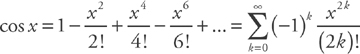 .
.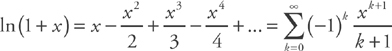
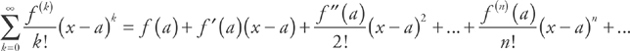
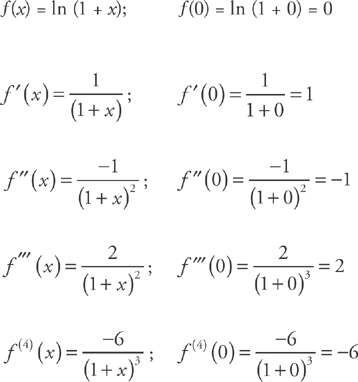
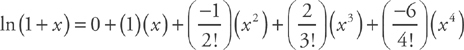 . This simplifies to
. This simplifies to 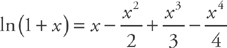 .
.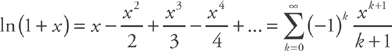 .
.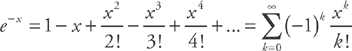
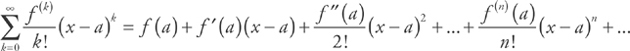
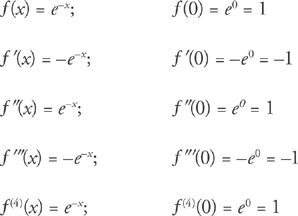

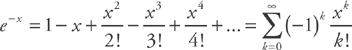 .
.
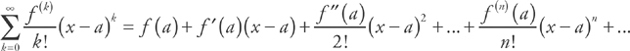

 , which simplifies to
, which simplifies to 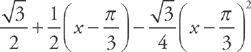 .
. ; the interval of convergence is
; the interval of convergence is 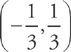 .
.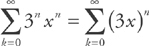 , so the common ratio is 3x. To find the interval of convergence, all
, so the common ratio is 3x. To find the interval of convergence, all  . Thus the interval of convergence is
. Thus the interval of convergence is 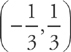 . The radius of convergence is simply the distance from the center of the interval to either endpoint, or half the width of the interval. In this case, the radius of convergence is
. The radius of convergence is simply the distance from the center of the interval to either endpoint, or half the width of the interval. In this case, the radius of convergence is 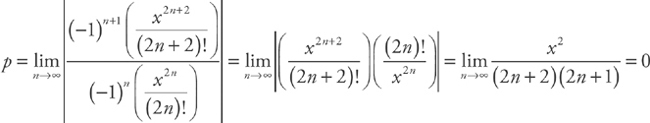 .
.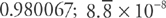
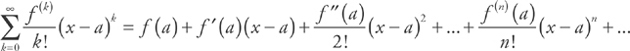

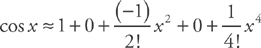 . This is the fourth degree Taylor polynomial. You should memorize the Taylor series that are highlighted on
. This is the fourth degree Taylor polynomial. You should memorize the Taylor series that are highlighted on  . To find the error bound, we can simply use the next term of the polynomial. Here, the next term is
. To find the error bound, we can simply use the next term of the polynomial. Here, the next term is 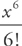 . If we plug in x = 0.2, we get:
. If we plug in x = 0.2, we get: 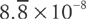 .
.

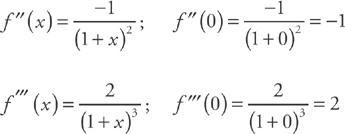
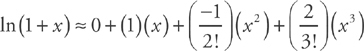 . This simplifies to
. This simplifies to 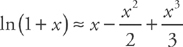 .
.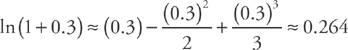 . To find the error bound, we can simply use the next term of the polynomial. Here, the next term is
. To find the error bound, we can simply use the next term of the polynomial. Here, the next term is 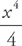 . If we plug in x = 0.3, we get: 0.002025.
. If we plug in x = 0.3, we get: 0.002025.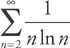 , so we need to see if
, so we need to see if 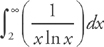 converges. First, we replace the upper limit with a
converges. First, we replace the upper limit with a 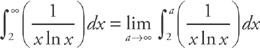 . Next, if we let u = ln x, then
. Next, if we let u = ln x, then 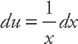 . Substituting into the integrand, we get:
. Substituting into the integrand, we get:  . Substituting back, we get:
. Substituting back, we get: 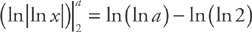 . Finally, we take the limit:
. Finally, we take the limit:  . Therefore, the series diverges by the Integral Test.
. Therefore, the series diverges by the Integral Test.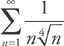 , so we need to see if
, so we need to see if 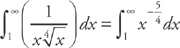 converges. First, we replace the upper limit with a and take the limit as a goes to infinity. We get:
converges. First, we replace the upper limit with a and take the limit as a goes to infinity. We get: 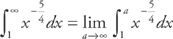 . Next, we integrate:
. Next, we integrate: 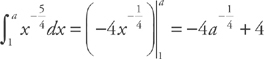 . Now, we take the limit:
. Now, we take the limit: 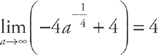 . Therefore, the series converges by the Integral Test.
. Therefore, the series converges by the Integral Test.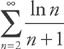 , which we can easily compare to the series
, which we can easily compare to the series 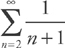 . The series
. The series 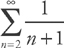 is essentially the harmonic series (it’s just missing the first two terms), which diverges. The series
is essentially the harmonic series (it’s just missing the first two terms), which diverges. The series 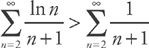 for all terms. Therefore, the series diverges by the Comparison Test.
for all terms. Therefore, the series diverges by the Comparison Test.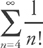 , which we can easily compare to the series
, which we can easily compare to the series  . The series
. The series 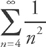 converges and the series
converges and the series 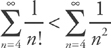 for all terms. Therefore, the series converges by the Comparison Test.
for all terms. Therefore, the series converges by the Comparison Test.