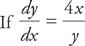and y(0) = 5, find an equation for y in terms of x.There are many types of differential equations, but only a very small number of them appear on the AP exam. There are courses devoted to learning how to solve a wide variety of differential equations, but AP calculus provides only a very basic introduction to the topic.
If you’re given an equation in which the derivative of a function is equal to some other function, you can determine the original function by integrating both sides of the equation and then solving for the constant term.
Example 1: If 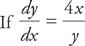and y(0) = 5, find an equation for y in terms of x.
The first step in solving these is to put all of the terms that contain y on the left side of the equals sign and all of the terms that contain x on the right side. We then have: y dy = 4x dx. The second step is to integrate both sides:
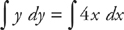
And then you integrate:
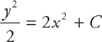
You’re not done yet. The final step is to solve for the constant by plugging in x = 0 and y = 5:
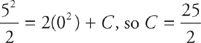
The solution is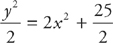 
.
That’s all there is to it. Separate the variables, integrate both sides, and solve for the constant. Often, the equation will involve a logarithm. Let’s do an example.
Example 2: If 
= 3x2y and y(0) = 2, find an equation for y in terms of x.
First, put the y terms on the left and the x terms on the right:
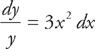
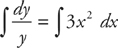
The result is: ln y = x3 + C. It’s customary to solve this equation for y. You can do this by putting both sides into exponential form:
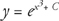
This can be rewritten as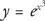 
and, because ec is a constant, the equation becomes:
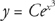
This is the preferred form of the equation. Now, solve for the constant. Plug in x = 0 and y = 2, and you get 2 = Ce0.
Because e0 = 1, C = 2. The solution is 
.
This is the typical differential equation that you’ll see on the AP exam. Other common problem types involve position, velocity, and acceleration or exponential growths and decay (Problem 4). We did several problems of this type in Chapter 10, before you knew how to use integrals. In a sample problem, you’re given the velocity and acceleration and told to find distance (the reverse of what we did before).
Example 3: If the acceleration of a particle is given by a(t) = –32 ft/sec2, and the velocity of the particle is 64 ft/sec and the height of the particle is 32 ft at time t = 0, find: (a) the equation of the particle’s velocity at time t; (b) the equation for the particle’s height, h, at time t; and (c) the maximum height of the particle.
Part A: Because acceleration is the rate of change of velocity with respect to time, you can write that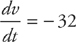 
. Now separate the variables and integrate both sides:
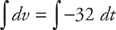
Integrating this expression, we get v = –32t + C. Now we can solve for the constant by plugging in t = 0 and v = 64. We get: 64 = –32(0) + C and C = 64. Thus, velocity is v = –32t + 64.
Part B: Because velocity is the rate of change of displacement with respect to time, you can write that:
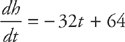
Separate the variables and integrate both sides:
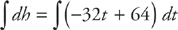
Integrate the expression: h = –16t2 + 64t + C. Now solve for the constant by plugging in t = 0 and h = 32:
32 = –16 (02) + 64(0) + C and C = 32
Thus, the equation for height is h = –16t2 + 64t + 32.
Part C: In order to find the maximum height, you need to take the derivative of the height with respect to time and set it equal to zero. Notice that the derivative of height with respect to time is the velocity; just set the velocity equal to zero and solve for t:
–32t + 64 = 0, so t = 2
Thus, at time t = 2, the height of the particle is a maximum. Now, plug t = 2 into the equation for height:
h = –16(2)2 + 64(2) + 32 = 96
Therefore, the maximum height of the particle is 96 feet.
Here are some solved problems. Do each problem, covering the answer first, then check your answer.
PROBLEM 1. If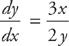 
and y(0) = 10, find an equation for y in terms of x.
Answer: First, separate the variables:
2y dy = 3x dx
Then, we take the integral of both sides:
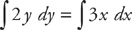
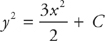
Finally, solve for the constant:
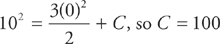
The solution is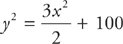 
.
PROBLEM 2. If = 4xy2 and y(0) = 1, find an equation for y in terms of x.
Answer: First, separate the variables: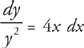 
and take the integral of both sides:
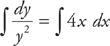
Next, integrate both sides: −
= 2x2 + C. You can rewrite this as: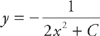 
Finally, solve for the constant:
The solution is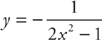 
.
PROBLEM 3. If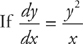 
and y(1) = 
, find an equation for y in terms of x.
Answer: This time, separating the variables gives us this: 
.
Then, take the integral of both sides: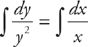 
.
Next, integrate both sides: − = ln x + C and rearrange:
Finally, solve for the constant: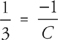 
, so C = –3. The solution is 
.
PROBLEM 4. A city had a population of 10,000 in 1980 and 13,000 in 1990. Assuming an exponential growth rate, estimate the city’s population in 2000.
Answer: The phrase “exponential growth rate” means that 
= ky, where k is a constant. Take the integral of both sides:
Then, integrate both sides: (ln y = kt + C) and put both sides in exponential form:
y = ekt+c = Cekt
Next, use the information about the population to solve for the constants. If you treat 1980 as t = 0 and 1990 as t = 10, then:
10,000 = Cek(0) and 13,000 = Cek(10)
So, C = 10,000 and k =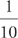 
ln 1.3 ≈ .0262.
The equation for population growth is approximately y = 10,000e.0262t. We can estimate that the population in 2000 will be:
y = 10,000e.0262(20) = 16,900
You are going to use your calculator to find an approximate answer to a differential equation. The method is quite simple. First, you need a starting point and an initial slope.
Next, we use increments of h to come up with approximations. Each new approximation will use the following rules:
xn = xn – 1 + h
yn = yn – 1 + h (y′n − 1)
Repeat for n = 1, 2, 3,…
This is much easier to understand if we do an example.
Example 1: Use Euler’s Method, with h = 0.2, to estimate y(1) if y′ = y – 2 and y(0) = 4.
We are given that the curve goes through the point (0, 4). We will call the coordinates of this point x0 = 0 and y0 = 4. The slope is found by y0 = 4 plugging into y′ = y – 2, so we have an initial slope of y′0 = 4 – 2 = 2.
Now we need to find the next set of points.
Step 1: Increase x0 by h to get x1:
x1 = 0.2
Step 2: Multiply h by y′0 and add to y0 to get y1:
y1 = 4 + 0.2(2) = 4.4
Step 3: Find y′1 by plugging y1 into the equation for y′ :
y′1 = 4.4 – 2 = 2.4
Repeat until you get to the desired point (in this case x = 1).
Step 1: Increase x1 by h to get x2:
x2 = 0.4
Step 2: Multiply h by y′1 and add to y1 to get y2:
y2 = 4.4 + 0.2(2.4) = 4.88
Step 3: Find y′2 by plugging y2 into the equation for y′ :
y′2 = 4.88 – 2 = 2.88
x3 = 0.6
Step 2: y3 = y2 + h(y′2):
y3 = 4.88 + 0.2(2.88) = 5.456
Step 3: y′3 = y3 – 2:
y′3 = 5.456 – 2 = 3.456
Step 1: x4 = x3 + h:
x4 = 0.8
Step 2: y4 = y3 + h(y′3):
y4 = 5.456 + 0.2(3.456) = 6.1472
Step 3: y′4 = y4 – 2:
y′4 = 6.1472 – 2 = 4.1472
Step 1: x5 = x4 + h:
x5 = 1.0
Step 2: y5 = y4 + h(y′4):
y5 = 6.1472 + 0.2(4.1472) = 6.97664
We don’t need to go any further because we are asked for the value of y when x = 1.
The answer is y = 6.97664
Let’s do another example.
Example 2: Use Euler’s Method, with h = 0.1, to estimate y(0.5) if y′ = y – 1 and y(0) = 3.
We start with x0 = 0 and y0 = 3. The slope is found by plugging y0 = 3 into y′ = y – 1, so we have an initial slope of y′0 = 3 – 1 = 2.
Step 1: Increase x0 by h to get x1:
x1 = 0.1
Step 2: Multiply h by y′0 and add to y0 to get y1:
y′1 = 3 + 0.1(2) = 3.2
Step 3: Find y′1 by plugging y1 into the equation for y′ :
y1 = 3.2 – 1 = 2.2
Step 1: x2 = x1 + h:
x2 = 0.2
Step 2: y2 = y1 + h(y′1):
y2 = 3.2 + 0.1(2.2) = 3.42
Step 3: y′2 = y2 – 1:
y′2 = 3.42 – 1 = 2.42
Step 1: x3 = x2 + h:
x3 = 0.3
Step 2: y3 = y2 + h(y′2):
y3 = 3.42 + 0.1(2.42) = 3.662
Step 3: y′3 = y3 – 1:
y′3 = 3.662 – 1 = 2.662
Step 1: x4 = x3 + h:
x4 = 0.4
Step 2: y4 = y3 + h(y′3):
y4 = 3.662 + 0.1(2.662) = 3.9282
Step 3: y′4 = y4 – 1:
y′4 = 3.9282 – 1 = 2.9282
Step 1: x5 = x4 + h:
x5 = 0.5
y5 = 3.9282 + 0.1(2.9282) = 4.22102
The answer is y = 4.22102.
Now try these on your own. Do each problem first with the answer covered, then check your answer.
PROBLEM 1: Use Euler’s Method, with h = 0.2, to estimate y(2) if y′ = 2y + 1 and y(1) = 5.
We start with x0 = 1 and y0 = 5. The slope is found by plugging y0 = 5 into y′ = 2y + 1, so we have an initial slope of y′0 = 2(5)+1= 11.
Step 1: Increase x0 by h to get x1:
x1 = 1.2
Step 2: Multiply h by y′0 and add to y0 to get y1:
y1 = 5 + .2(11) = 7.2
Step 3: Find y′1 by plugging y1 into the equation for y′ :
y′1 = 2(7.2) + 1 = 15.4
Step 1: x2 = x1 + h:
x2 = 1.4
Step 2: y2 = y1 + h(y′1):
y2 = 7.2 + 0.2(15.4) = 10.28
Step 3: y′2 = 2y2 + 1:
y′2 = 2(10.28) + 1 = 21.56
Step 1: x3 = x2 + h:
x3 = 1.6
Step 2: y3 = y2 + h(y′2):
y3 = 10.28 + 0.2(21.56) = 14.592
y′3 = 2(14.592) + 1 = 30.184
Step 1: x4 = x3 + h:
x4 = 1.8
Step 2: y4 = y3 + h(y′3):
y4 = 14.592 + 0.2(30.184) = 20.6288
Step 3: y′4 = 2y4 + 1:
y′4 = 2(20.6288) + 1 = 42.2576
Step 1: x5 = x4 + h:
x5 = 2
Step 2: y5 = y4 + h(y′4):
y5 = 20.6288 + 0.2(42.2576) = 29.08032
The answer is y = 29.08032.
PROBLEM 2: Use Euler’s Method, with h = 0.1, to estimate y(0.5) if y′ = y2 + 1 and y(0) = 0.
We start with x0 = 0 and y0 = 0. The slope is found by plugging y0 = 0 into y′ = y2 + 1, so we have an initial slope of y′0 = 1.
Step 1: Increase x0 by h to get x1:
x1 = 0.1
Step 2: Multiply h by y′0 and add to y0 to get y1:
y1 = 0 + 0.1(1) = 0.1
Step 3: Find y′1 by plugging y1 into the equation for y′ :
y′1 = (0.1)2 + 1 = 1.01
Step 1: x2 = x1 + h:
x2 = 0.2
y2 = 0.1 + 0.1(1.01) = 0.201
Step 3: y′2 = (y2)2 + 1:
y′2 = (0.201)2 + 1 = 1.040
Step 1: x3 = x2 + h:
x3 = 0.3
Step 2: y3 = y2 + h(y′2):
y′3 = 0.201 + 0.1(1.040) = 0.305
Step 3: y′3 = (y3)2 + 1:
y′3 = (0.305)2 + 1 = 1.093
Step 1: x4 = x3 + h:
x4 = 0.4
Step 2: y4 = y3 + h(y′3):
y4 = 0.305 + 0.1(1.093) = 0.414
Step 3: y′4 = (y4)2 + 1:
y′4 = (0.414)2 + 1 = 1.171
Step 1: x5 = x4 + h:
x5 = 0.5
Step 2: y5 = y4 + h(y′4):
y5 = 0.414 + 0.1(1.171) = 0.531
The answer is y = 0.531.
The idea behind slope fields, also known as direction fields, is to make a graphical representation of the slope of a function at various points in the plane. We are given a differential equation, but not the equation itself. So how do we do this? Well, it’s always easiest to start with an example.
Example 1: Given = x, sketch the slope field of the function.
What does this mean? Look at the equation. It gives us the derivative of the function, which is the slope of the tangent line to the curve at any point x. In other words, the equation tells us that the slope of the curve at any point x is the x value at that point.
For example, the slope of the curve at x = 1 is 1. The slope of the curve at x = 2 is 2. The slope of the curve at the origin is 0. The slope of the curve at x = –1 is –1. We will now represent these different slopes by drawing small segments of the tangent lines at those points. Let’s make a sketch:
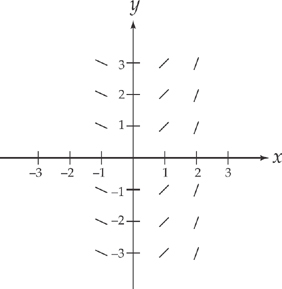
See how all of these slopes are independent of the y values, so for each value of x, the slope is the same vertically, but is different horizontally. Compare this slope field to the next example.
Example 2: Given = y, sketch the slope field of the function.
Here, the slope of the curve at y = 1 is 1. The slope of the curve at y = 2 is 2. The slope of the curve at the origin is 0. The slope of the curve at y = –1 is –1. Let’s make a sketch.
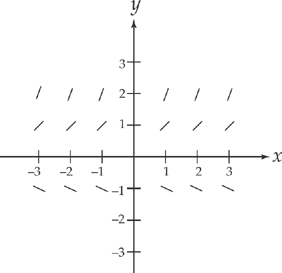
See how all of these slopes are independent of the x values, so for each value of y, the slope is the same horizontally, but is different vertically.
Now let’s do a slightly harder example.
Example 3: Given = xy, sketch the slope field of the function.
Now, we have to think about both the x and y values at each point. Let’s calculate a few slopes.
At (0,0), the slope is (0)(0) = 0.
At (1,0), the slope is (1)(0) = 0.
At (2,0), the slope is (2)(0) = 0.
At (0,1), the slope is (0)(1) = 0.
At (0,2), the slope is (0)(2) = 0.
So the slope will be zero at any point on the coordinate axes.
At (1,1), the slope is (1)(1) = 1.
At (1,2), the slope is (1)(2) = 2.
At (1,–1), the slope is (1)(–1) = –1.
At (1,–2), the slope is (1)(–2) = –2.
So the slope at any point where x = 1 will be the y value. Similarly, you should see that the slope at any point where y = 1 will be the x value. As we move out the coordinate axes, slopes will get steeper—whether positive or negative.
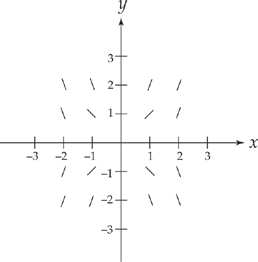
Let’s do one more example.
Example 4: Given = y – x, sketch the slope field of the function.
We have to think about both the x and y values at each point. This time, let’s make a table of the values of the slope at different points.
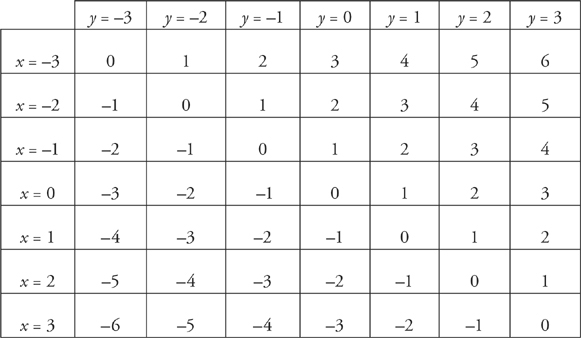
Now, let’s make a sketch of the slope field. Notice that the slopes are zero along the line y = x and that the slopes get steeper as we move away from the line in either direction.
That’s really all that there is to slope fields. Obviously, there are more complicated slope fields that one could come up with, but on the AP exam, they will ask you to sketch only the simplest ones.
Now try these problems. The answers are in Chapter 23.
1. If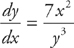 
and y(3) = 2, find an equation for y in terms of x.
2. If 
and y(0) = 6, find an equation for y in terms of x.
3. If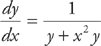 
and y(0) = 2, find an equation for y in terms of x.
4. If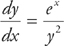 
and y(0) = 1, find an equation for y in terms of x.
5. If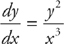 
and y(1) = 2, find an equation for y in terms of x.
6. If 
and y(0) =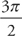 
, find an equation for y in terms of x.
7. A colony of bacteria grows exponentially and the colony’s population is 4,000 at time t = 0 and 6,500 at time t = 3. How big is the population at time t = 10?
8. A rock is thrown upward with an initial velocity, v(t), of 18 m/s from a height, h(t), of 45 m. If the acceleration of the rock is a constant –9 m/s2, find the height of the rock at time t = 4.
9. The rate of growth of the volume of a sphere is proportional to its volume. If the volume of the sphere is initially 36π ft3, and expands to 90π ft3 after 1 second, find the volume of the sphere after 3 seconds.
10. A radioactive element decays exponentially in proportion to its mass. One-half of its original amount remains after 5,750 years. If 10,000 grams of the element are present initially, how much will be left after 1,000 years?
11. Use Euler’s Method, with h = 0.25, to estimate y(1) if y′ = y – x and y(0) = 2.
12. Use Euler’s Method, with h = 0.2, to estimate y(1) if y′ = –y and y(0) = 1.
13. Use Euler’s Method, with h = 0.1, to estimate y(0.5) if y′ = 4x3 and y(0) = 0.
14. Sketch the slope field for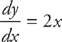 
.
15. Sketch the slope field for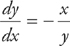 
.
16. Sketch the slope field for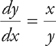 
.