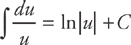
You’ve learned how to integrate polynomials and some of the trig functions (there are more of them to come), and you have the first technique of integration: u-substitution. Now it’s time to learn how to integrate some other functions—namely, exponential and logarithmic functions. Yes, the long-awaited second part of Chapter 11. The first integral is the natural logarithm:
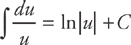
Notice the absolute value in the logarithm. This ensures that you aren’t taking the logarithm of a negative number. If you know that the term you’re taking the log of is positive (for example, x2 + 1), we can dispense with the absolute value marks. Let’s do some examples.
Example 1: Find 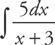 .
.
Whenever an integrand contains a fraction, check to see if the integral is a logarithm. Usually, the process involves u-substitution. Let u = x + 3 and du = dx. Then:
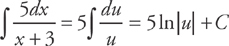
Substituting back, the final result is:
5 ln |x + 3| + C
Example 2: Find 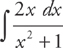 .
.
Let u = x2 + 1 du = 2x dx and substitute into the integrand:
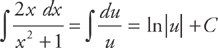
Then substitute back:
ln (x2 + 1) + C
Remember when we started antiderivatives and we didn’t do the integral of tangent, cotangent, secant, or cosecant? Well, their time has come.
Example 3: Find 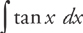 .
.
First, rewrite this integral as
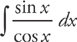
Now we let u = cos x and du = – sin x dx and substitute:
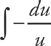
Now, integrate and re-substitute:
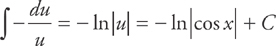
Thus,  .
.
Example 4: Find 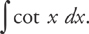
Just as before, rewrite this integral in terms of sine and cosine:
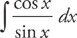
Now we let u = sin x and du = cos x dx and substitute:

Now, integrate:
ln |u| + C = ln |sin x| + C
Therefore,  . This looks a lot like the previous example, doesn’t it?
. This looks a lot like the previous example, doesn’t it?
Example 5: Find 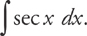
You could rewrite this integral as:
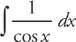
However, if you try u-substitution at this point, it won’t work. So what should you do? You’ll probably never guess, so we’ll show you: Multiply the sec x by 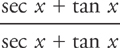 . This gives you:
. This gives you:
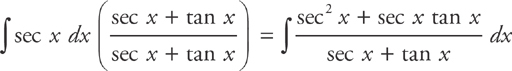
Now you can do u-substitution. Let u = sec x + tan x du = (sec x tan x + sec2 x) dx.
Then rewrite the integral as:
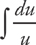
Pretty slick, huh?
The rest goes according to plan as you integrate:
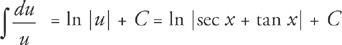
Therefore, 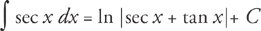 .
.
Example 6: Find 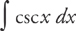 .
.
You guessed it! Multiply csc x by 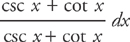 . This gives you:
. This gives you:
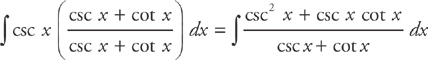
Let u = csc x + cot x and du = (– csc x cot x – csc2 x) dx. And, just as in Example 5, you can rewrite the integral as:
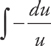
And integrate:
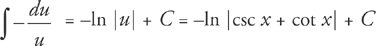
Therefore, ∫ csc x dx = –ln |csc x + cot x| + C.
As we do more integrals, the natural log will turn up over and over. It’s important that you get good at recognizing when integrating requires the use of the natural log.
Now let’s learn how to find the integral of ex. Remember that 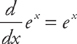 ? Well, you should be able to predict the formula below:
? Well, you should be able to predict the formula below:
∫ eu du = eu + C
As with the natural logarithm, most of these integrals use u-substitution.
Example 7: Find ∫e7x dx.
Let u = 7x, du = 7dx, and  du = dx. Then you have:
du = dx. Then you have:
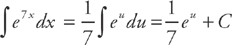
Substituting back, you get:

In fact, whenever you see ∫ekx dx, where k is a constant, the integral is:

Example 8: Find 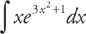 .
.
Let u = 3x2 + 1, du = 6x dx, and  du = x dx. The result is:
du = x dx. The result is:
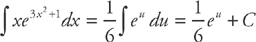
Now it’s time to put the x’s back in:
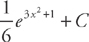
Example 9: Find 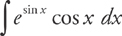 .
.
Let u = sin x and du = cos x dx. The substitution here couldn’t be simpler:

As you can see, these integrals are pretty straightforward. The key is to use u-substitution to transform nasty-looking integrals into simple ones.
There’s another type of exponential function whose integral you’ll have to find occasionally:
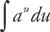
As you should recall from your rules of logarithms and exponents, the term au can be written as e u ln a. Because ln a is a constant, we can transform  into
into 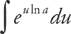 . If you integrate this, you’ll get:
. If you integrate this, you’ll get:
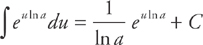
Now substituting back au for e u ln a:
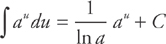
Example 10: Find  .
.
Follow the rule we just derived:
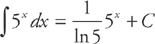
Because these integrals don’t show up too often on the AP exam, this is the last you’ll see of them in this book. You should, however, be able to integrate them using the rule, or by converting them into a form of 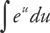 .
.
Try these on your own. Do each problem with the answers covered, then check your answer.
PROBLEM 1. Evaluate 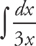 .
.
Answer: Move the constant term outside of the integral, like this:
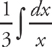
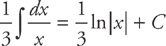
PROBLEM 2. Evaluate 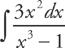 .
.
Answer: Let u = x3 – 1 and du = 3x2 dx, and substitute:
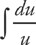
Now integrate:
ln |u| + C
And substitute back:
ln |x3 – 1| + C
PROBLEM 3. Evaluate 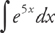 .
.
Answer: Let u = 5x and du = 5dx. Then  du = dx. Substitute in:
du = dx. Substitute in:
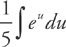
Integrate:

And substitute back:

PROBLEM 4. Evaluate  .
.
Answer: Let u = 3x and du = 3dx. Then  du = dx. Make the substitution:
du = dx. Make the substitution:

Integrate according to the rule. Your result should be:
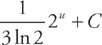
Now get back to the expression as a function of x:

Evaluate the following integrals. The answers are in Chapter 23.