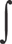 , which stands for integration. An integral actually serves several different purposes, but the first, and most basic, is that of the antiderivative.
, which stands for integration. An integral actually serves several different purposes, but the first, and most basic, is that of the antiderivative.Welcome to the other half of calculus! This, unfortunately, is the more difficult half, but don’t worry. We’ll get you through it. In differential calculus, you learned all of the fun things that you can do with the derivative. Now you’ll learn to do the reverse: how to take an integral. As you might imagine, there’s a bunch of new fun things that you can do with integrals, too.
It’s also time for a new symbol 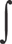 , which stands for integration. An integral actually serves several different purposes, but the first, and most basic, is that of the antiderivative.
, which stands for integration. An integral actually serves several different purposes, but the first, and most basic, is that of the antiderivative.
An antiderivative is a derivative in reverse. Therefore, we’re going to reverse some of the rules we learned with derivatives and apply them to integrals. For example, we know that the derivative of x2 is 2x. We use antidifferentiation if we’re given the derivative of a function and we have to figure out the original function. Thus, the antiderivative of 2x is x2. (Actually, the answer is slightly more complicated than that, but we’ll get into that in a few moments.)
Now we need to add some info here to make sure that you get this absolutely correct. First, as far as notation goes, it is traditional to write the antiderivative of a function using its upper case letter, so the antiderivative of f(x) is F(x), the antiderivative of g(x) is G(x), and so on.
The second idea is very important: Each function has more than one antiderivative. In fact, there are an infinite number of antiderivatives of a function. Let’s go back to our example to help illustrate this.
Remember that the antiderivative of 2x is x2? Well, consider: If you take the derivative of x2 + 1, you get 2x. The same is true for x2 + 2, x2 – 1, and so on. In fact, if any constant is added to x2, the derivative is still 2x because the derivative of a constant is zero.
Because of this, we write the antiderivative of 2x as x2 + C; where C stands for any constant.
Finally, whenever you take the integral (or antiderivative) of a function of x, you always add the term dx (or dy if it’s a function of y, etc.) to the integrand (the thing inside the integral). You’ll learn why later.
For now, just remember that you must always use the dx symbol, and teachers love to take points off for forgetting the dx. Don’t ask why, but they do!
Here is the Power Rule for antiderivatives:
If f(x) = xn, then  (except when n = –1).
(except when n = –1).
Example 1: Find 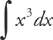 .
.
Using the Power Rule, we get:
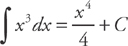
Don’t forget the constant C, or your teachers will take points off for that, too!
Example 2: Find  .
.
The Power Rule works with negative exponents, too:
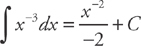
Not terribly hard, is it? Now it’s time for a few more rules that look remarkably similar to the rules for derivatives that we saw in Chapter 6:

Here are a few more examples to make you an expert:
Example 3: 
Example 4: 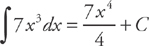
Example 6: 
The integrals of some trigonometric functions follow directly from the derivative formulas in Chapter 8.
We didn’t mention the integrals of tangent, cotangent, secant, and cosecant, because you need to know some rules about logarithms to figure them out. We’ll get to them in a few chapters. Notice also that each of the answers is divided by a constant. This is to account for the Chain Rule. Let’s do some examples.

Example 7: Check the integral  by differentiating the answer.
by differentiating the answer.

Notice how the constant is accounted for in the answer?
Example 8: 
Example 9: 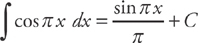
Example 10: 
If you’re not sure if you have the correct answer when you take an integral, you can always check by differentiating the answer and seeing if you get what you started with. Try to get in the habit of doing that at the beginning, because it’ll help you build confidence in your ability to find integrals properly. You’ll see that, although you can differentiate just about any expression that you’ll normally encounter, you won’t be able to integrate many of the functions you see.
By using the rules for addition and subtraction, we can integrate most polynomials.
Example 11: Find 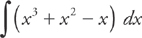 .
.
We can break this into separate integrals, which gives us:

Now you can integrate each of these individually:

You can combine the constants into one constant (it doesn’t matter how many C’s we use, because their sum is one collective constant whose derivative is zero):

Sometimes you’ll be given information about the function you’re seeking that will enable you to solve for the constant. Often, this is an “initial value,” which is the value of the function when the variable is zero. As we’ve seen, normally there are an infinite number of solutions for an integral, but when we solve for the constant, there’s only one.
Example 12: Find the equation of y where  = 3x + 5 and y = 6 when x = 0.
= 3x + 5 and y = 6 when x = 0.
Let’s put this in integral form:

Integrating, we get:

Now we can solve for the constant because we know that y = 6 when x = 0:

Therefore, C = 6 and the equation is:
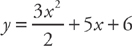
Example 13: Find f(x) if f′(x) = sin x – cos x and f(π) = 3.
Integrate f′(x):

Now solve for the constant:
3 = −cos(π) − sin(π) + C
C = 2
Therefore, the equation becomes:
f(x) = – cos x – sin x + 2
Now we’ve covered the basics of integration. However, integration is a very sophisticated topic and there are many types of integrals that will cause you trouble. We will need several techniques to learn how to evaluate these integrals. The first and most important is called u-substitution, which we will cover in the second half of this chapter.
In the meantime, here are some solved problems. Do each problem, covering the answer first, then check your answer.
PROBLEM 1. Evaluate  .
.
Answer: Here’s the Power Rule again:

Using the rule:

PROBLEM 2. Evaluate 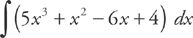 .
.
Answer: We can break this up into several integrals:
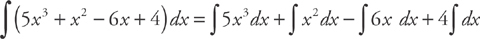
Each of these can be integrated according to the Power Rule:

This can be rewritten:

Notice that we combine the constant terms into one constant term C.
PROBLEM 3. Evaluate  .
.
Answer: First, expand the integrand:
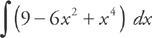
Break this up into several integrals:
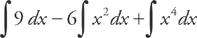
And integrate according to the Power Rule:

PROBLEM 4. Evaluate 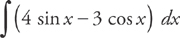 .
.
Answer: Break this problem into two integrals:

Each of these trig integrals can be evaluated according to its rule:
−4 cos x − 3 sin x + C
PROBLEM 5. 
Answer: Break the integral in two:
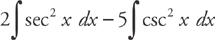
Each of these trig integrals can be evaluated according to its rule:
2 tan x + 5 cot x + C
Now evaluate the following integrals. The answers are in Chapter 23.
When we discussed differentiation, one of the most important techniques we mastered was the Chain Rule. Now, you’ll learn the integration corollary of the Chain Rule (called u-substitution), which we use when the integrand is a composite function. All you do is replace the function with u, and then you can integrate the simpler function using the Power Rule (as shown below):
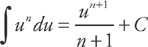
Suppose you have to integrate  . You could expand out this function and integrate each term, but that’ll take a while. Instead, you can follow these four steps:
. You could expand out this function and integrate each term, but that’ll take a while. Instead, you can follow these four steps:
Step 1: Let u = x – 4. Then  = 1 (rearrange this to get du = dx).
= 1 (rearrange this to get du = dx).
Step 2: Substitute u = x – 4 and du = dx into the integrand:

Step 3: Integrate:
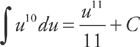
Step 4: Substitute back for u:

That’s u-substitution. The main difficulty you’ll have will be picking the appropriate function to set equal to u. The best way to get better is to practice. The object is to pick a function and replace it with u, then take the derivative of u to find du. If we can’t replace all of the terms in the integrand, we can’t do the substitution.
Let’s do some examples.
Once again, you could expand this out and integrate each term, but that would be difficult. Use u-substitution.
Let u = 5x2 – 3. Then  = 10x and du = 10x dx. Now substitute:
= 10x and du = 10x dx. Now substitute:

And integrate:
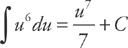
Substituting back gives you:
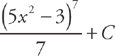
Confirm that this is the integral by differentiating  :
:
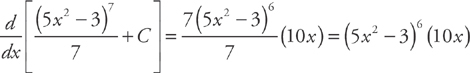
Example 2: 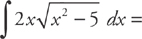
If u = x2 – 5, then  = 2x and du = 2x dx. Substitute u into the integrand:
= 2x and du = 2x dx. Substitute u into the integrand:

Integrate:
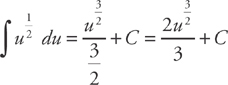
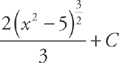
Note: From now on, we’re not going to rearrange  ; we’ll go directly to “du =” format. You should be able to do that step on your own.
; we’ll go directly to “du =” format. You should be able to do that step on your own.
Example 3: 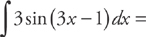
Let u = 3x – 1. Then du = 3dx. Substitute the u in the integral:

Figure out the integral:

And throw the x’s back in:
– cos(3x – 1) + C
So far, this is only the simplest kind of u-substitution; naturally, the process can get worse when the substitution isn’t as easy. Usually, you’ll have to insert a constant term to put the integrand into a workable form. For example:
Example 4: 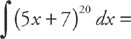
Let u = 5x + 7. Then du = 5 dx. Notice that we can’t do the substitution immediately because we need to substitute for dx and we have 5 dx. No problem: Because 5 is a constant, just solve for dx:
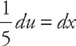
Now you can substitute:
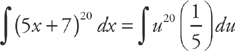
Rearrange the integral and solve:

And now it’s time to substitute back:

Example 5: 
Let u = 3x2 + 1. Then du = 6x dx. We need to substitute for x dx, so we can rearrange the du term:

Now substitute:

Evaluate the integral:
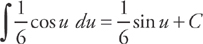
And substitute back:

Example 6: 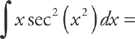
Let u = x2. Then du = 2x dx and  du = x dx.
du = x dx.
Substitute:

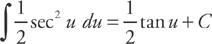
Now the original function goes back in:
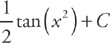
This is a good technique to master, so practice on the following solved problems. Do each problem, covering the answer first, then check your answer.
PROBLEM 1. Evaluate  .
.
Answer: Let u = 3x and du = 3dx. Then  du = dx.
du = dx.
Substitute and integrate:
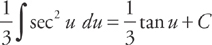
Then substitute back:
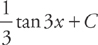
PROBLEM 2. Evaluate 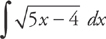 .
.
Answer: Let u = 5x – 4 and du = 5dx. Then  du = dx.
du = dx.
Substitute and integrate:

Then substitute back:

Answer: Let u = 4x2 – 7 and du = 8x dx. Then  du = x dx.
du = x dx.
Substitute and integrate:
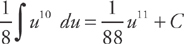
Then substitute back:

PROBLEM 4. Evaluate  .
.
Answer: Let 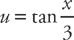 and
and 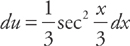 . Then
. Then  .
.
Substituting, we get:
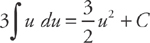
Then substitute back:

Now evaluate the following integrals. The answers are in Chapter 23.