A. Riemann Sums
- You should be able to find the area under a curve using left, right, and midpoint evaluations and the Trapezoidal Rule.
- You should know the fundamental theorem of calculus:
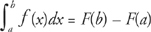
• General Overview of This Book
AP Calculus is divided into two types: AB and BC. The former is supposed to be the equivalent of a semester of college calculus; the latter, a year. In truth, AB calculus covers closer to three quarters of a year of college calculus. In fact, the main difference between the two is that BC calculus tests some more theoretical aspects of calculus and it covers a few additional topics. In addition, BC calculus is harder than AB calculus. The AB exam usually tests straightforward problems in each topic. They’re not too tricky and they don’t vary very much. The BC exam asks harder questions. But neither exam is tricky in the sense that the SAT is. Nor do they test esoteric aspects of calculus. Rather, both tests tend to focus on testing whether you’ve learned the basics of differential and integral calculus. The tests are difficult because of the breadth of topics that they cover, not the depth. You will probably find that many of the problems in this book seem easier than the problems you’ve had in school. This is because your teacher is giving you problems that are harder than those on the AP.
Now, some words about the test itself. The AP exam comes in two parts. First, there is a section of multiple-choice questions covering a variety of calculus topics. The multiple choice section has two parts. Part A consists of 28 questions; you are not permitted to use a calculator on this section. Part B consists of 17 questions; you are permitted to use a calculator on this part. These two parts comprise a total of 45 questions.
After this, there is a free response section consisting of six questions, each of which requires you to write out the solutions and the steps by which you solved it. You are permitted to use a calculator for the first two problems but not for the four other problems. Partial credit is given for various steps in the solution of each problem. You’ll usually be required to sketch a graph in one of the questions. The College Board does you a big favor here: You may use a graphing calculator. In fact, The College Board recommends it! And they allow you to use programs as well. But here’s the truth about calculus: Most of the time, you don’t need the calculator anyway. Remember: These are the people who bring you the SAT. Any gift from them should be regarded skeptically!
Topics in italics are BC Topics. This list is drawn from the topical outline for AP calculus furnished by the College Board. You might find that your teacher covers some additional topics, or omits some, in your course. Some of the topics are very broad, so we cannot guarantee that this book covers these topics exhaustively.
I. Functions, Graphs, and Limits
A. Analysis of Graphs
B. Limits
C. Asymptotes
D. Continuity
E. Parametric, Polar, and Vector Functions
II. Differential Calculus
A. The Definition of the Derivative
B. Derivative at a Point
C. Derivative of a Function
D. Second Derivative
E. Applications of Derivatives
F. More Applications of Derivatives
G. Computation of Derivatives
III. Integral Calculus
A. Riemann Sums
B. Applications of Integrals
C. Fundamental Theorem of Calculus
D. Techniques of Antidifferentiation
E. Applications of Antidifferentiation
IV. Polynomial Approximations and Series
A. The Concept of a Series
B. Series Concepts
C. Taylor Series
 .
.The key to doing well on the exam is to memorize a variety of techniques for solving calculus problems, and to recognize when to use them. There’s so much to learn in AP calculus that it’s difficult to remember everything. Instead, you should be able to derive or figure out how to do certain things based on your mastery of a few essential techniques. In addition, you’ll be expected to remember a lot of the math that you did before calculus—particularly trigonometry. You should be able to graph functions, find zeros, derivatives, and integrals with the calculator.
Furthermore, if you can’t derive certain formulae, you should memorize them! A lot of students don’t bother to memorize the trigonometry special angles and formulae because they can do them on their calculators. This is a big mistake. You’ll be expected to be very good with these in calculus, and if you can’t recall them easily, you’ll be slowed down and the problems will seem much harder. Make sure that you’re also comfortable with analytic geometry. If you rely on your calculator to graph for you, you’ll get a lot of questions wrong because you won’t recognize the curves when you see them.
This advice is going to seem backward compared to what your teachers are telling you. In school you’re often yelled at for memorizing things. Teachers tell you to understand the concepts, not just memorize the answers. Well, things are different here. The understanding will come later, after you’re comfortable with the mechanics. In the meantime, you should learn techniques and practice them, and, through repetition, you will ingrain them in your memory.
Each chapter is divided into three types of problems: examples, solved problems, and practice problems. The first type is contained in the explanatory portion of the unit. The examples are designed to further your understanding of the subject and to show you how to get the problems right. Each step of the solution to the example is worked out, except for some simple algebraic and arithmetic steps that should come easily to you at this point.
The second type is solved problems. The solutions are worked out in approximately the same detail as the examples. Before you start work on each of these, cover the solution with an index card or something, then check the solution afterward. And you should read through the solution, not just assume that you knew what you were doing because your answer was correct.
The third type of problem is practice problems. Only the answers to them are given. We hope you’ll find that each chapter offers enough practice problems for you to be comfortable with the material. The topics that are emphasized on the exam have more problems; those that are de-emphasized have fewer. In other words, if a chapter has only a few practice problems, it’s not an important topic on the AP exam and you shouldn’t worry too much about it.
Different colleges use AP Exams in different ways, so it is important that you go to a particular college’s web site to determine how it uses AP Exams. The three items below represent the main ways in which AP Exam scores can be used:
There are many resources available to help you improve your score on the AP Calculus Exam, not the least of which are your teachers. If you are taking an AP class, you may be able to get extra attention from your teacher, such as obtaining feedback on your essays. If you are not in an AP course, reach out to a teacher who teaches calculus, and ask if the teacher will review your free response questions or otherwise help you with content.
Another wonderful resource is AP Central, the official site of the AP Exams. The scope of the information at this site is quite broad and includes:
The AP Central home page address is: http://apcentral.collegeboard.com/apc/Controller.jpf.
The AP Calculus AB Exam Course home page address is: http://apcentral.collegeboard.com/apc/public/courses/teachers_corner/2178.html
The AP Calculus BC Exam Course home page address is: http://apcentral.collegeboard.com/apc/public/courses/teachers_corner/2118.html
Finally, The Princeton Review offers tutoring and small group instruction. Our expert instructors can help you refine your strategic approach and add to your content knowledge. For more information, call 1-800-2REVIEW.
As part of the Introduction, you identified some areas of potential improvement. Let’s now delve further into your performance on Test 1, with the goal of developing a study plan appropriate to your needs and time commitment.
Read the answers and explanations associated with the Multiple Choice questions (starting at this page). After you have done so, respond to the following questions: